基本顶弹性基础边界薄板模型分析(I)——初次破断

谢生荣，陈冬冬，孙颜顶，郜明明，孙运江，施　伟

(中国矿业大学(北京)资源与安全工程学院，北京　100083)



基本顶弹性基础边界薄板模型分析(I)
——初次破断

谢生荣，陈冬冬，孙颜顶，郜明明，孙运江，施伟

(中国矿业大学(北京)资源与安全工程学院，北京100083)

摘要:建立基本顶弹性基础边界弹性薄板力学模型，运用偏微分方程有限差分方法，研究了推进步距、弹性基础系数、基本顶厚度与弹性模量对基本顶主弯矩与破断位置的影响，得出:基本顶厚度或弹性模量增大时，中部最大主弯矩Mz增大、长边与短边绝对值最大主弯矩Mc，Md减小;步距增大时，Mz，Mc，Md均增大、Mz增长幅度较小;弹性基础系数增大时，Mz减小、Mc，Md增大;根据主弯矩破断准则得出:推进步距或弹性基础系数小时基本顶中部先破断、反之长边超前煤壁先破断;基本顶厚度或弹性模量小时长边超前煤壁先破断、反之中部先断裂。基本顶厚度或弹性模量越大超前断裂距离越大;弹性基础系数或步距越大超前断裂距离越小。弹性基础边界时，基本顶存在3类破断顺序:①长边—中部—短边;②长边—短边—中部;③中部—长边—短边。

关键词:基本顶;弹性基础;初次破断;弹性薄板;有限差分法

谢生荣，陈冬冬，孙颜顶，等．基本顶弹性基础边界薄板模型分析(I)——初次破断［J］．煤炭学报，2016，41(6):1360－1368．doi: 10．13225/j．cnki．jccs．2016．0197

Xie Shengrong，Chen Dongdong，Sun Yanding，et al．Analysis on thin plate model of basic roof at elastic foundation boundary(I):First breaking［J］．Journal of China Coal Society，2016，41(6):1360－1368．doi:10．13225/j．cnki．jccs．2016．0197

采场顶板的破断形态及规律，对指导工作面安全回采等意义重大。为研究顶板的破断失稳规律及控制方法，学者们提出了传递岩梁理论、砌体梁理论、关键层理论等［1］;研究了固支、简支、自由边界条件时基本顶的破断规律、并提出四边刚性固支时基本顶长边先破坏最终形成“O－X”型的破断形态［1－3］;理论计算了四边固支条件下大倾角煤层基本顶破断模式［4］;研究了弹性薄板条件下顶板的破断机理及形态等［5－7］;运用相似模拟、数值模拟、物探法等研究基本顶及上覆岩层破断运动规律［8－11］;引入弹性地基边界条件研究岩梁的超前断裂问题［12－13］，运用有限元方法在基本顶边界附加刚度子矩阵的方式模拟了基本顶的破断形态及矿压规律［14］;四边固支条件下引入弹性地基研究密实充填时基本顶力学特征［15］。

根据采场实际工程地质条件，基本顶处在上、下岩层的夹支状态，特别是基本顶的下层依次为直接顶和煤层，且均可变形，当直接顶、煤层较软且厚度较大时，基本顶下侧煤岩层限制基本顶运动的能力很弱，无法实现刚性固支，此种条件下就不适合再采用四边刚性固支的边界条件来研究基本顶的破断规律。

针对以上存在的问题，且根据煤层抗剪切能力弱、强度低、变形能力大的特点［1，12］，可以把基本顶看做处在弹性基础上的薄板，建立弹性基础边界条件时的弹性薄板力学模型，运用有限差分方法研究基本顶的内力分布及破断规律。这对从实际角度出发全面分析基本顶的破断规律并指导安全回采很有实际理论意义和实用价值。

1　弹性基础边界薄板力学模型

1.1力学模型的建立

开采区域上方基本顶所受载荷为自身与上覆软岩层的自重之和［1］，设为q。

1.1.1基本顶边界条件模型

如图1所示，从岩体剖面角度描述基本顶边界条件力学模型，L表示工作面跨度之半。图1(a)为基本顶固支边界条件模型，它是假设基本顶上覆岩层为刚度无穷大岩体，基本顶下伏直接顶、煤层及底板岩层也为刚度无穷大岩体，即煤壁边界处基本顶的各个位置设定为刚性固支边界条件。

图1(b)为基本顶实际围岩关系模型，基本顶的上覆岩层一般是弹性模量为E2的软岩层、总厚度为h2，更上层为亚关键层;基本顶的下伏岩层是厚度为h1、弹性模量模为E1的直接顶，更下层为弹性模量为E3、厚度为h3的煤层，一般基本顶下伏岩层的弹性模量E1，E3都较小［1］，对基本顶向下位移的限制能力十分有限，即煤层较软时，超前煤壁前方会有更大范围的基本顶压缩煤层向下位移，所以此种情况下不满足刚性固支边界条件。当基本顶下伏岩层的弹模很大、且强度很大时，下伏岩层限制基本向下位移的能力强，同时基本顶上覆岩层的弹性模量和强度也很大时，可以上下均很好的限制基本顶的位移，方可近似满足刚性固支边界条件。

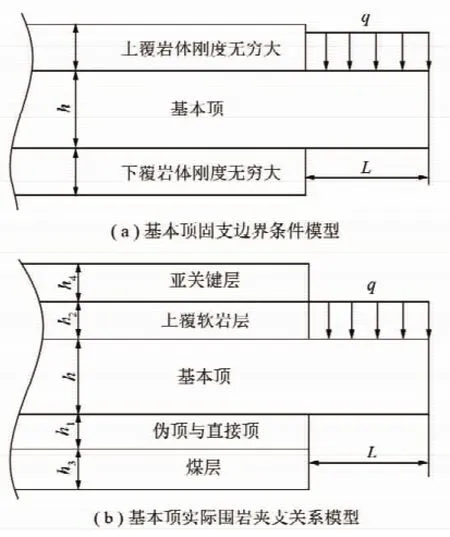
图1　基本顶两类边界条件Fig.1　Two boundary conditions of basic roof

1.1.2基本顶弹性基础边界

由上述分析可见，基本顶处在上、下岩层的夹支状态，上覆岩层主要限制基本顶向上位移、下伏岩层主要限制基本顶向下位移，基本顶实际边界应该更符合弹性固支边界条件而不是刚性固支边界条件［1］，如图2所示。实际上基本顶下伏岩体的刚度是限制位移的关键，所以引入文克尔弹性地基［1，15］力学模型，且基本顶上下均假设为弹性岩层，上覆岩层的刚度系数为ks、下伏岩层的刚度系数为kz。

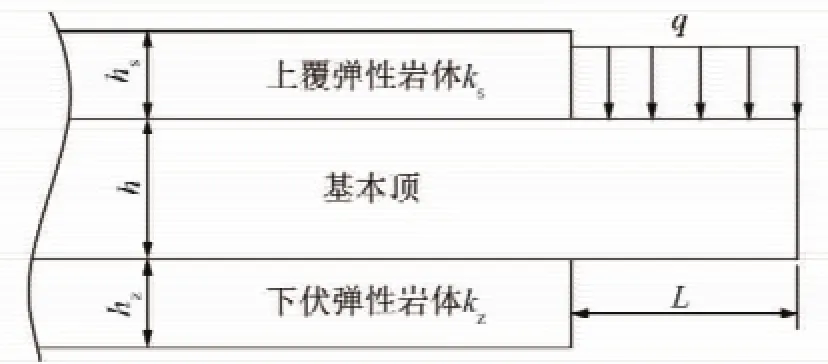
图2　基本顶弹性基础边界模型Fig.2　Elastic foundation boundary model of basic roof

当基本顶上、下位置岩层刚度都很大时，弹性基础系数k由下式［12］确定k=kz+ks。

下伏岩层中限制基本顶移动能力最弱的一般是煤层，则煤层的刚度系数是此种力学模型最关键影响因素，特别是煤层较软时弹性基础系数 k可由下式［12］确定，即可只考虑煤层刚度的影响。

式中，hs为上覆弹性岩体厚度;hz为下伏岩体厚度。

1.1.3基本顶弹性基础边界力学模型的建立

由弹性薄板力学假设［17］:

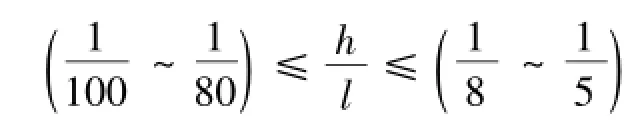
式中，h为板的厚度，m;l为板的短边长度，m;一般采场基本顶均满足上述条件所以可视为弹性薄板［15］。

由此建立弹性基础边界条件下基本顶弹性薄板力学模型，该力学模型可这么认为:一无限大的弹性基本顶放在有切口的(实际中是开切眼或开采区域即S1区，其余为S2区)无限大弹性地基上，且开采区上方基本顶四周受到弹性层的夹支，此区域上方的基本顶受到软岩层载荷和自重作用。由于基本顶无限大，则从开切眼向四周无限远处必定存在基本顶的挠度和转角均为零处，所以可以取定基本顶的外边界条件为无穷远处挠度为0、转角为0。

如图3所示基本顶弹性基础边界力学模型，弹性地基上有一块区域(ABCD相当于切眼或开采区域、AB为工作面长度、AD为工作面推进距离)，此区域上基本顶受到的载荷为其自重q1与上覆软岩层的分布载荷q2之和(其中，q1+q2=q)。

开切眼区域上方基本顶的挠度微分方程为

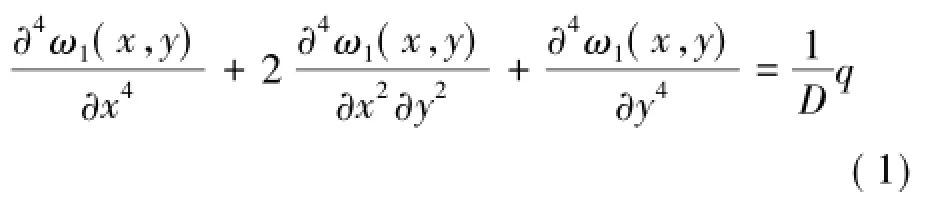
式中，ω1(x，y)为S1区域的基本顶挠度函数;D为基本顶刚度。

开切眼或开采区域之外的基本顶挠度方程为

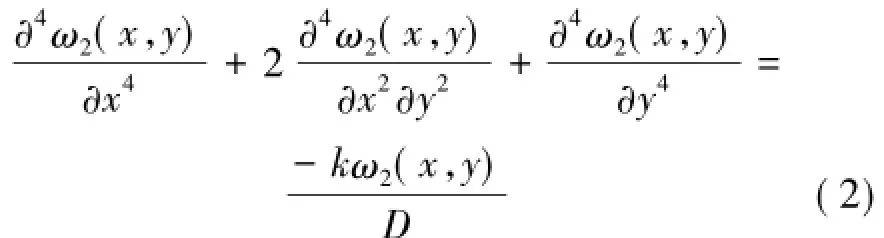
式中，ω2(x，y)为S2区域的基本顶挠度函数。

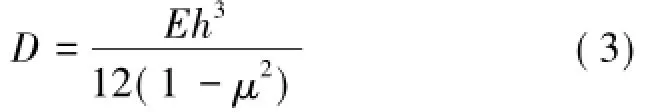
式中，h为基本顶厚度，m;μ为泊松比;E为弹性模量，GPa。

1.2边界条件

1.2.1内边界的边界条件

AB，AD，BC，DC边是基本顶弹性基础起始边界，属于方程(1)与(2)，在四边上挠度和转角分别连续，即满足式(4)，同时弯矩、剪力也分别连续。

图3　基本顶弹性基础边界力学模型Fig.3　Elastic foundation boundary mechanics model of main roof

1.2.2外边界的边界条件

基本顶的无穷远处的边界条件为:挠度为0，转角为0，即以A1B1C1D1为刚性固支边界，各边界上各点满足:挠度为0，转角为0，如式(5)所示，其中A1B1长为2x0，A1D1长为2y0。

但是在解微分方程时不好利用这个条件，而实际上可以确定的是，工作面自开切眼推进，因开采影响范围有限［1］，自开切眼向四周一定范围内一定存在基本顶的挠度和转角可以近似视为0的点，以此处作为刚性固支边界，此时即可利用具体边界条件解对应的偏微分方程。

所以这里，x0与y0根据计算模型可取有限值，即满足工程尺度要求、且满足偏微分方程的近似解即可。

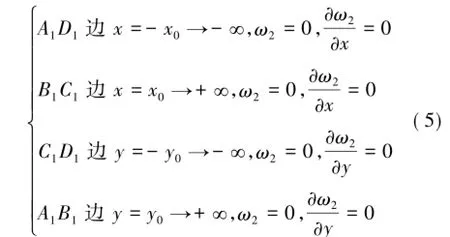
2　弹性基础薄板模型计算方法

要得出满足上述所给边界条件的偏微分方程的精确解极为困难，所以采取近似计算方法求得近似解。而有限差分方法是计算偏微分方程近似解的有效方法［17－19］。

2.1偏微分方程有限差分方法

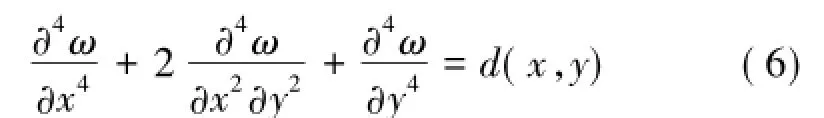
由式(6)所示基本的偏微分方程，建立如图4所示的偏微分方程13点有限差分网格分布图，其中P0节点是13点差分网格中的典型节点且每个网格的尺寸满足m=Δx=Δy，建立差分格式为

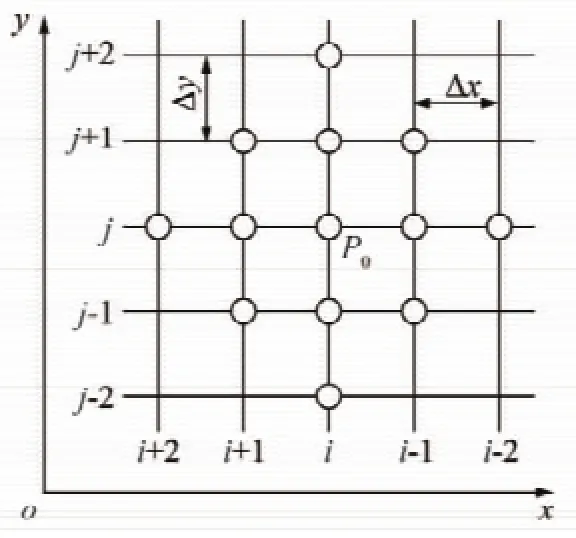
图4　偏微分方程有限差分法节点分布Fig.4　Finite difference method node distribution of partial differential equation

其差分展开式为

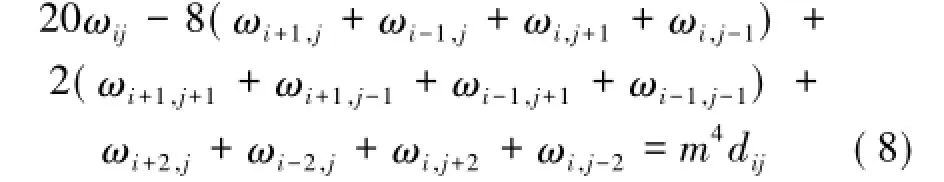
2.2挠度方程的差分方程

由上述偏微分方程有限差分法，可得式(1)在典型节点P0的差分方程式为

2.3外边界条件方程的差分方程

式(5)为外边界条件的精确边界条件表达式，即x与y均趋近于无穷远处满足挠度与转角为0，事实上从方程的近似解和工程要求的角度来看，x0，y0取有限值即可满足要求，这也为用有限差分法解微分方程提供了便利的条件，所以在式(11)中也采取了有限边界的表达方式，给出了对应典型节点P0边界条件方程的差分方程式。

2.4解算偏微分方程过程

根据上述建立的差分方程可知，任意差分方程中挠度未知的节点至多13个，通过对各个未知挠度的节点建立13点差分方程，组建代数方程组，通过解方程组便可得到各个节点的挠度解。

上述求解过程可通过如图5所示方法实现:采用Matlab软件［19］中的sparse函数构造系数为稀疏矩阵组建代数方程组，然后调用gmres函数求解这个方程组，从而得到各个未知节点的挠度解。

求出挠度解是求取其他内力分量的关键，因为弹性薄板的内力分量均是通过对挠度求偏导的方法得到。如式(12)所示为由典型节点P0的挠度解求取典型节点各内力分量的方法。

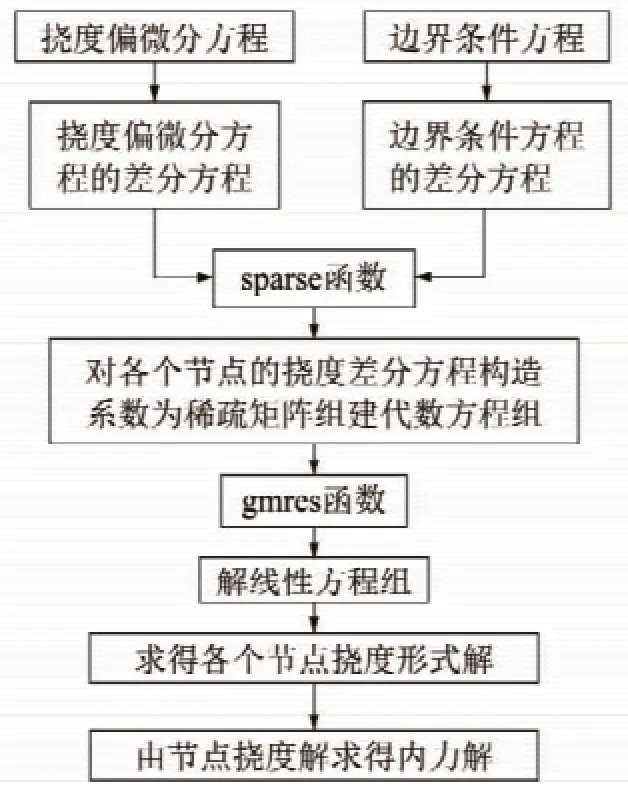
图5　解偏微分方程过程Fig.5　Process of solving partial differential equations

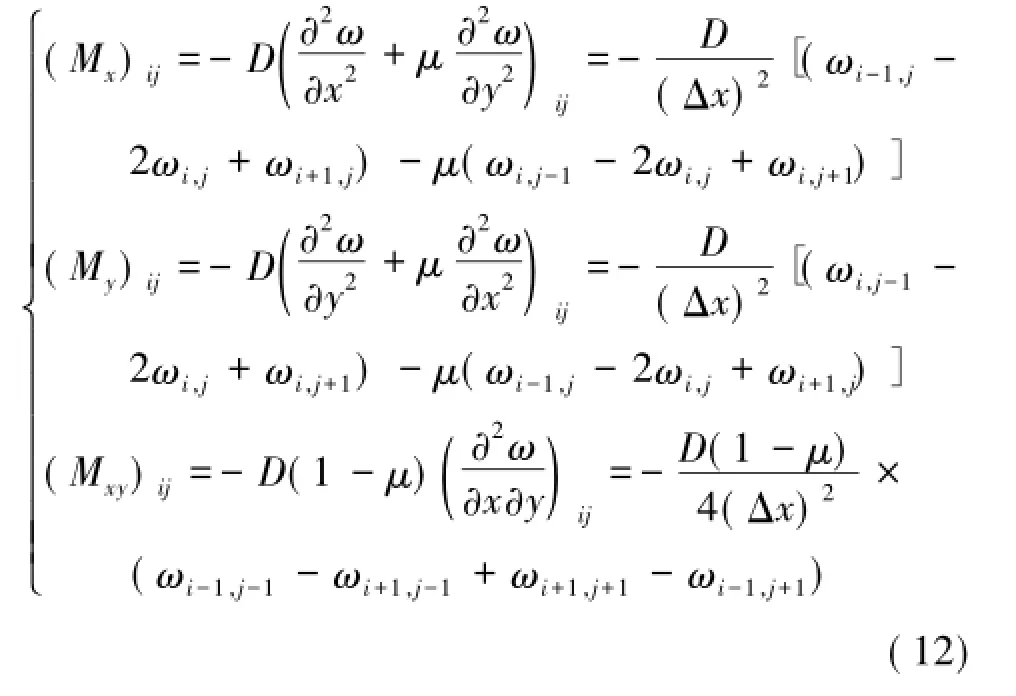
3　弹性基础薄板模型计算结果分析

按照上述计算方法，来设定计算模型的尺寸，工作面的长度为120 m、根据工程实际问题的需要及计算精度，计算模型的外边界A1B1C1D1的长度是工作面长度的3倍，取长宽均为360 m、长宽均划分为730格，在所研究参数范围内可满足计算要求。

3.1破断指标的确定

由于岩石材料的抗拉能力远小于抗压能力，可采用岩石的抗拉强度作为破断判别标准［1］，设基本顶上某点的应力状态为(σx，σy，τxy)、基本顶上任意微单元体的弯矩为(Mx，My，Mxy)，其关系如下。

最大、最小主应力为

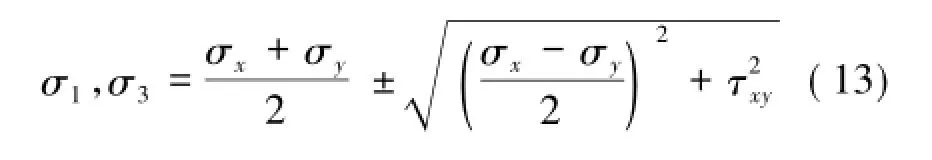
最大、最小主弯矩为

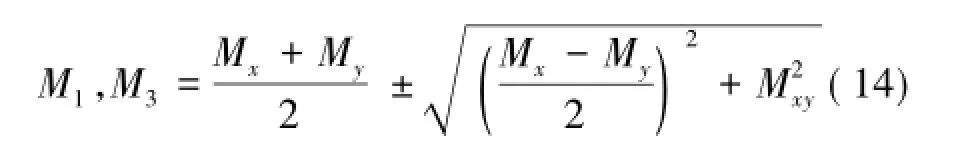
主应力与主弯矩之间的关系为

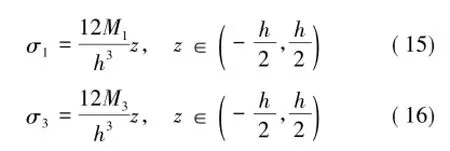
而抗拉能力与主弯矩之间的力学关系式为

由式(15)，(16)，(17)可知，基本顶上、下表面对应点的主应力大小相等方向相反、且是该截面上主应力值最大的点;而上、下表面点的主应力与主弯矩成正比例关系，所以可用主弯矩所在的位置分析基本顶的破断位置、且用有限差分法解算时更加方便。

由此确定了破断判据的分析指标，即运用主弯矩来分析基本顶的内力以及可能的断裂位置。

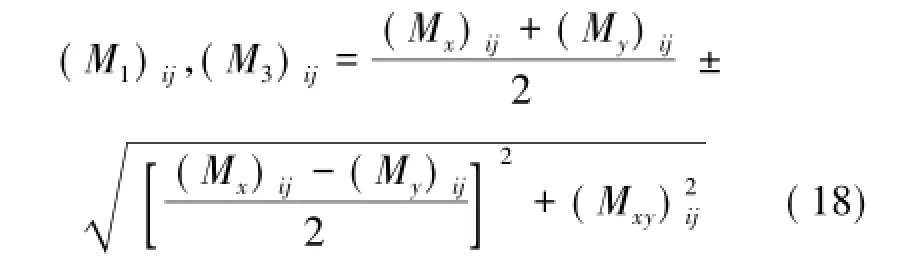
运用Matlab软件通过式(12)求各个节点内力分量，在通过式(18)求各个节点主弯矩，并把各个节点的最大主弯矩与最小主弯矩分别提取绘制。

3.2弹性基础边界主弯矩分布特征

选取某一特征参数分析研究弹性基础边界条件下基本顶主弯矩分布形态及规律，取工作面长度120 m、步距40 m(推进距离)、弹性模量30 GPa、厚度6 m、泊松比0.2、总载荷0.25 MPa、弹性基础系数为3 000 MN/m3。

根据式(18)求取并绘制基本顶各个节点最大主弯矩M1、最小主弯矩M3的分布形态图。图6(a)为基本顶各个节点的最小主弯矩M3的分布云图，图6(b)为基本顶各个节点最大主弯矩M1的分布云图。由图6知基本顶各个节点主弯矩M1，M3的分布规律:开采区域上方基本顶中部各个节点的最大主弯矩M1与最小主弯矩M3均为正弯矩，即此区域基本顶上表面受压应力、下表面受拉应力;长边、短边超前煤壁区的主弯矩M1，M3均为负弯矩，即此区域基本顶上表面受拉应力下表面受压应力。由岩石抗压不抗拉性质可知，基本顶中部的下表面与长边、短边超前煤壁区的上表面是最易先破坏的位置。

基本顶长边、短边绝对值最大的主弯矩是最小主弯矩M3的负值，且位置并不是处在与煤壁交界处而是超前煤壁位置;基本顶中部绝对值最大的弯矩是最大主弯矩M1。

弹性基础边界、不同几何及力学参数条件下基本顶的主弯矩分布形态与图6相似。由于所研究弹性薄板的对称性，薄板的上下表面的主应力大小相等、方向相反。所以分析主弯矩中绝对值最大的主弯矩即可来判断破断位置。

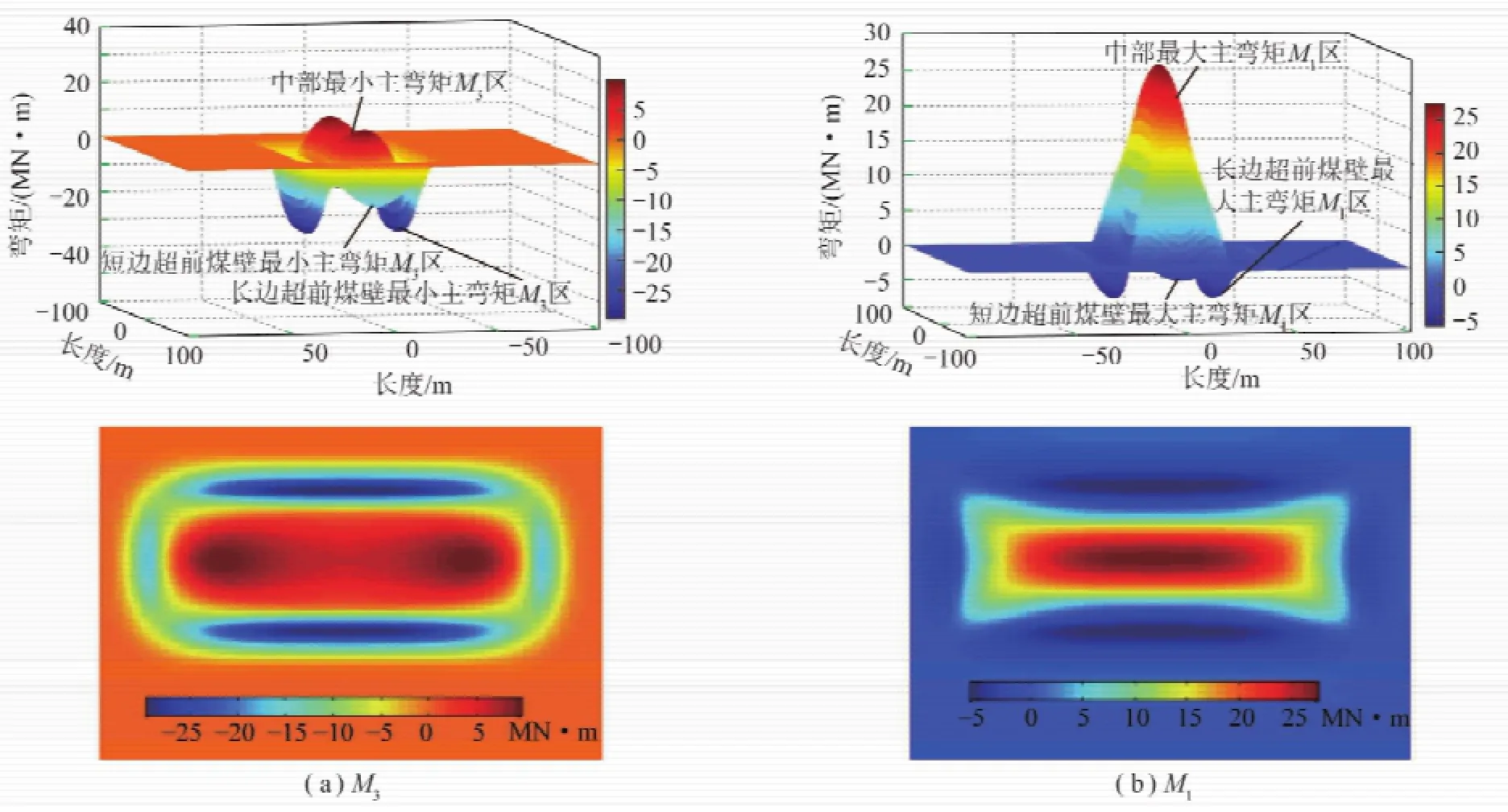
图6　基本顶主弯矩云图Fig.6　Basic roof main bending moment nephogram

根据上述分析并结合图3(a)建立如图7所示的基本顶弹性基础边界薄板模型时的关键主弯矩位置示意图，长边区域各个节点的绝对值最大主弯矩为最小主弯矩M3(为负弯矩)的绝对值、设为Mc，Lc为Mc超前煤壁距离;短边区域绝对值最大主弯矩为最小主弯矩M3(为负弯矩)的绝对值、设为Md，Ld为Md超前煤壁距离;中部绝对值最大主弯矩为最大主弯矩M1(为正弯矩)、设为Mz，并设基本顶可承载的极限弯矩为M0。

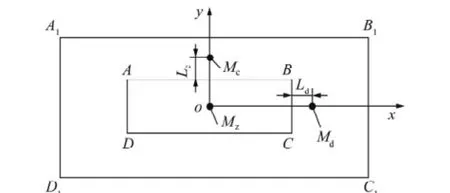
图7　基本顶关键主弯矩位置Fig.7　Chart of the key main bending moment position of main roof

那么，弹性基础边界条件下，基本顶的初次破断规律主要由长边Mc、中部Mz、短边Md的大小决定。按照上述计算方法，下面具体研究推进步距、弹性基础系数、基本顶的厚度及弹性模量的变化对主弯矩Mz，Mc，Md的影响由此分析弹性基础边界条件下基本顶的初次破断规律。

以下计算所采用的计算参数，未经说明及更改的均为:基本顶弹性模量E为30 GPa、泊松比0.2，长度120 m、步距40 m、厚度6 m、基本顶自身与上覆软岩层的总载荷设为0.25 MPa，即q为0.25 MPa、弹性基础系数k为3 000 MN/m3。

3.3破断位置的推进步距效应

推进步距是工作面的总推进距离，即图3或图7中的边AD的长度。

(1)长边Mc超前煤壁距离Lc。基本顶长边绝对值最大主弯矩Mc超前煤壁距离Lc随步距增大而逐渐减小，且随步距增大减小幅度相对降低(图8)。基本顶的短边Md超前煤壁距离Ld满足类似规律。

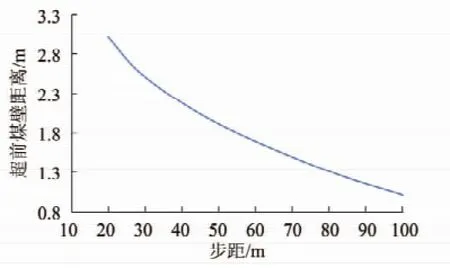
图8　Lc随步距变化曲线Fig.8　Curve of Lcchanging with the step distance

(2)主弯矩变化规律。推进步距越大，基本顶受到的主弯矩也越大，能推进更大的距离、显然基本顶需要更高的极限弯矩M0。若M0较小，则推进步距较小时，基本顶所受到的主弯矩即可达到极限弯矩M0;当M0较大，则步距较大时才会达到基本顶的极限弯矩M0。而推进步距不同时，3个主弯矩Mz，Mc，Md的变化规律和幅度有区别，所以破断位置会不同。

图9为推进步距不同时基本顶主弯矩变化曲线。随着推进步距增大，主弯矩Mz，Mc，Md均增大，超前煤壁区的主弯矩Mc，Md增长幅度大于基本顶中部主弯矩Mz。步距较小时，如图9中小于L1时Mc＜Mz、且步距增大时两者的差值在减小，此时若Mz大于基本顶极限弯矩M0，则基本顶中部先破断;推进步距大于L1时 Mc＞Mz，且步距增大两者差值增大，此时若Mc大于基本顶极限弯矩M0，则长边超前煤壁先断裂;步距继续增大到大于L2时Mc＞Md＞Mz，即基本顶长边与短边所受到的主弯矩均超过中部的，长边与短边超前煤壁位置会先于中部破断。

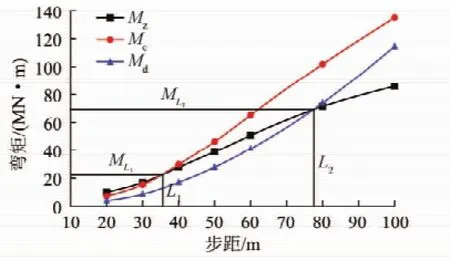
图9　主弯矩随步距变化规律Fig.9　Variation of the main bending moment with the step distance

3.4破断位置的弹性基础系数效应

(1)长边Mc超前煤壁距离Lc。如图10所示，随弹性基础系数k值增大，基本顶长边主弯矩Mc超前煤壁距离Lc逐渐减小，即随弹性固支能力增大，基本顶长边最小主弯矩向煤壁转移，基本顶短边也存在相同规律。

图10　Lc随k值变化曲线Fig.10　Curve of Lcwith the chang of k value

(2)主弯矩变化规律。如图11所示，弹性基础系数不同主弯矩变化规律曲线。随着弹性基础系数k的增大，基本顶中部主弯矩Mz减小且减小幅度降低、基本顶长边与短边主弯矩Mc，Md逐渐增大。即弹性基础系数k增大，弹性固支能力增强，主弯矩由中部向长边、短边超前煤壁区转移。

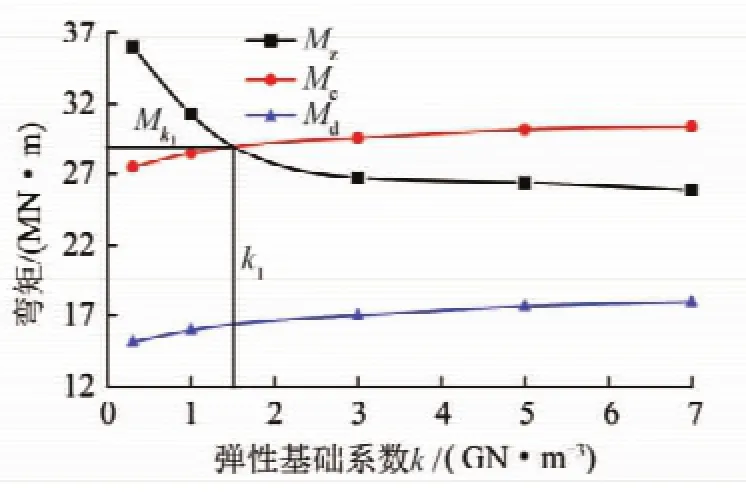
图11　主弯矩随k值的变化规律Fig.11　Variation law of the main bending moment with the k value

k小于k1时主弯矩Mz＞Mc、并且随k值增大两者的差值减小，此时若Mz大于基本顶极限弯矩M0，则基本顶的中部先破断;k大于k1时Mz＜Mc、并且随k值增大两者差值增大，此时若Mc大于基本顶极限弯矩M0，则基本顶长边超前煤壁区先破断。短边的最小主弯矩绝对值Md均小于长边的最小主弯矩绝对值Mc，即长边总比短边先达到弯矩极限而破断。

3.5破断位置的基本顶厚度效应

(1)长边Mc超前煤壁距离Lc。如图12所示，随基本顶厚度增大，长边主弯矩Mc超前煤壁距离Lc越大，即基本顶厚度越大，发生超前断裂时的位置距离煤壁越远。

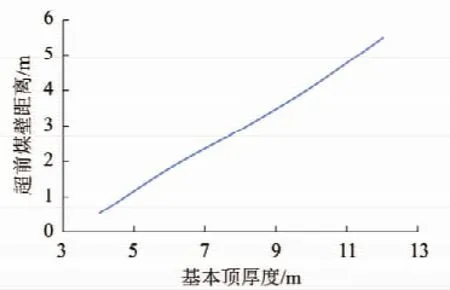
图12　Lc随基本顶厚度变化曲线Fig.12　Curve of Lcwith the change of the basic roof thickness

(2)主弯矩变化规律。如图13所示，随基本顶厚度增大，中部主弯矩Mz增大、长边与短边超前煤壁区主弯矩Mc与Md逐渐减小。当基本顶厚度较小时，如图中h＜h1时，长边超前煤壁区主弯矩Mc大于中部主弯矩Mz，此时若Mc大于基本顶极限弯矩M0，则先发生长边超前煤壁断裂;当基本顶厚度较大时，如图中h＞h1时，Mc小于中部主弯矩Mz，此时若达到基本顶极限弯矩M0，则基本顶中部先发生破断。

3.6破断位置的基本顶弹性模量效应

(1)长边Mc超前煤壁距离Lc。如图14所示，随基本顶弹性模量增大，长边主弯矩Mc超前煤壁距离Lc不断增大，即基本顶弹性模量越大，长边超前断裂时的断裂线距离煤壁越远。

图13　主弯矩随基本顶厚度变化规律Fig.13　Variation of the main bending moment with the thickness of the main roof

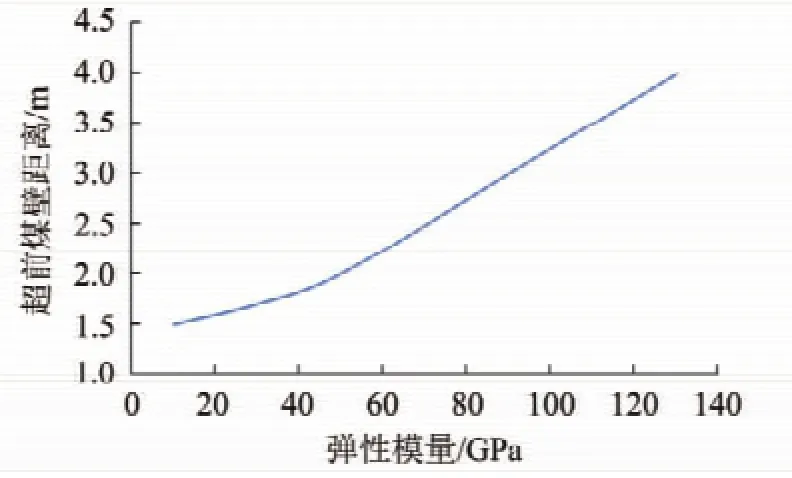
图14　Lc随基本顶弹性模量E变化曲线Fig.14　Curve of Lcwith the change of E

(2)主弯矩变化规律。图15为基本顶弹性模量E不同主弯矩变化曲线图。随E值增大，基本顶短边和长边主弯矩Mc，Md均逐渐降低、基本顶中部主弯矩Mz逐渐增大。

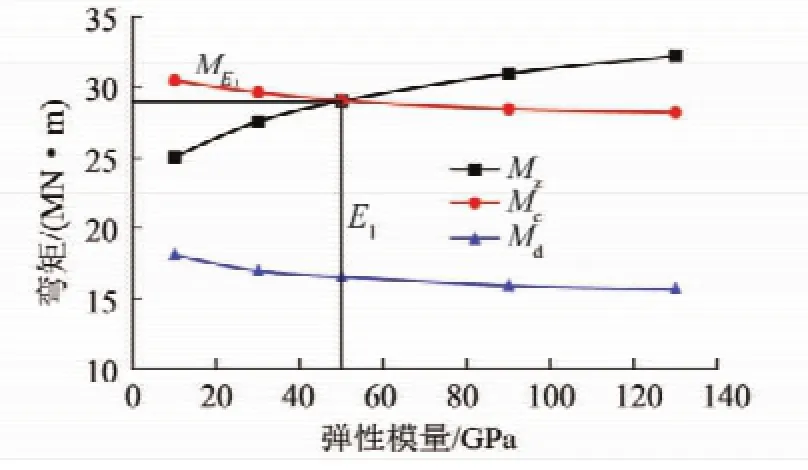
图15　主弯矩随基本顶弹性模量E变化规律Fig.15　Variation regularity of the main bending moment with the elastic modulus E

当基本顶的弹性模量E较小，图15中E＜E1时长边主弯矩Mc大于基本顶中部主弯矩Mz，即先发生长边超前煤壁断裂;当弹性模量E较大，图14中E＞E1时，中部主弯矩Mz大于长边主弯矩Mc，即先发生中部断裂;当基本顶的弹性模量处于上述两者之间时，存在Mc与Mz相等，即可能发生基本顶的长边与中部同时断裂的情况。

3.7弹性基础边界板模型基本顶破断规律

由上述分析可知，弹性基础边界条件下，基本顶首先破断的位置为中部或者长边超前煤壁位置，这与引入弹性基础边界基本顶梁模型得到的结果［12］及通过有限元模拟的方法得到的结果［14］一致。

根据主弯矩破断准则得出弹性基础边界时基本顶初次破断规律，推进步距或弹性基础系数较小先发生基本顶中部断裂、反之先发生长边超前煤壁断裂;厚度或弹性模量小时先发生长边超前煤壁断裂、反之先发生中部断裂，且得出如图16所示的弹性基础边界条件下基本顶的3类破断顺序(虚线表示破断线)。图16(a)基本顶破断顺序为:长边超前煤壁Lc破断—中部破断—短边超前煤壁Ld破断并逐步贯通;图16(b)破断顺序为:长边超前煤壁Lc破断—短边超前煤壁Ld破断—中部破断并逐步贯通(此种破断顺序和四边固支边界条件时的结论一致);图16(c)破断顺序为:中部破断—长边超前煤壁Lc破断—短边超前煤壁Ld破断并逐步贯通，上述裂隙最终贯通均形成“O－X”形破断形态。

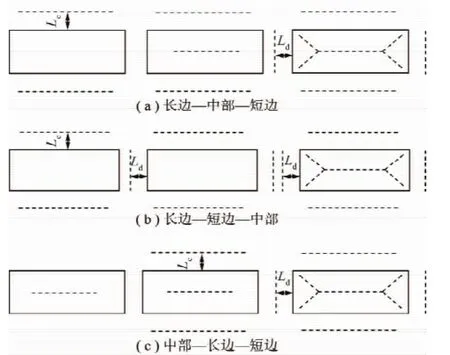
图16　弹性基础边界基本顶破断规律Fig.16　Basic roof breaking regularity with the elastic foundation boundary

图16中，若长边是工作面推进边则形成的是竖“O－X”形破断，若短边是工作面的推进边则最终形成的是横“O－X”形破断。把弹性基础边界条件与四边固支边界条件下得出的基本顶的破断规律进行对比，最终的破断形态基本一致，区别在于基本顶的破断顺序不同，以及长边、短边破断时的断裂线距离煤壁的距离不同。固支边界条件时，长边、短边破断线在煤壁处;弹性基础边界条件时，长边、短边的破断线在超前煤壁位置，而且超前煤壁距离的大小如上所述具备一定规律性。

4　结　　论

(1)建立基本顶弹性基础边界弹性薄板力学模型，运用偏微分方程有限差分方法，研究了步距、弹性基础系数、基本顶厚度与弹性模量对基本顶主弯矩及破断位置的影响。基本顶厚度或弹性模量增大时，中部最大主弯矩Mz增大、长边与短边绝对值最大主弯矩Mc，Md减小;步距增大时，Mz，Mc，Md均增大、Mz增长幅度较小;弹性基础系数增大时，Mz减小、Mc，Md增大。

(2)根据主弯矩破断准则得出弹性基础边界时基本顶初次破断规律，推进步距或弹性基础系数小时，基本顶中部先破断、反之长边超前煤壁先破断;厚度或弹性模量小时长边超前煤壁先破断、反之中部先破断。

(3)基本顶先发生长边超前煤壁断裂时，基本顶厚度或弹性模量越大超前断裂距离越大;弹性基础系数或步距越大超前断裂距离越小。

(4)弹性基础边界时基本顶存在3类破断顺序:①长边—中部—短边;②长边—短边—中部;③中部—长边—短边。有益补充了基本顶的初次破断顺序。

参考文献:

［1］钱鸣高，石平五，许家林．矿山压力与岩层控制［M］．徐州:中国矿业大学出版社，2010．

［2］浦海，黄耀光，陈荣华．采场顶板“X－O”型断裂形态力学分析［J］．中国矿业大学学报，2011，40(6):835－840．Pu Hai，Huang Yaoguang，Chen Ronghua．Mechanical analysis for “X－O”type fracture morphology of stope roof［J］．Journal of China University of Mining＆Technology，2011，40(6):835－840．

［3］刘洪磊，杨天鸿，张鹏海，等．复杂地质条件下煤层顶板“O－X”型破断及矿压显现规律［J］．采矿与安全工程学报，2015，32(5):793－800．Liu Honglei，Yang Tianhong，Zhang Penghai，et al．“O－X”failure pattern of roof and strata-pressure behavior under complex geological conditions［J］．Journal of Mining＆Safety Engineering，2015，32(5):793－800．

［4］王金安，张基伟，高小明，等．大倾角厚煤层长壁综放开采基本顶破断模式及演化过程(I)——初次破断［J］．煤炭学报，2015，40(6):1353－1360．Wang Jin’an，Zhang Jiwei，Gao Xiaoming，et al．Fracture mode and evolutionofmainroofstratumabovelongwallfully mechanized top coal caving in steeply inclined thick coal seam(I)—Initial fracture［J］．Journal of China Coal Society，2015，40(6): 1353－1360．

［5］贾喜荣，翟英达．采场薄板矿压理论与实践综述［J］．矿山压力与顶板管理，1999，16(3/4):22－25．Jia Xirong，Zhai Yingda．The review of groundpressure theory of thin slab in coal mining and its application［J］．Ground Pressure and Strata Control，1999，16(3/4):22－25．

［6］王红卫，陈忠辉，杜泽超，等．弹性薄板理论在地下采场顶板变化规律研究中的应用［J］．岩石力学与工程学报，2006，25(S2): 3769－3774．Wang Hongwei，Chen Zhonghui，Du Zechao，et al．Application ofelastic thin plate theory to change rule of roof in underground stope ［J］．Chinese Journal of Rock Mechanics and Enginering，2006，25(S2):3769－3774．

［7］李肖音，高峰，钟卫平．基于板模型的采场顶板破断机理分析［J］．采矿与安全工程学报，2008，25(2):180－183．Li Xiaoyin，Gao Feng，Zhong Weiping．Analysis of fracturing mechanism of stope roof based on plate model［J］．Journal of Mining ＆Safety Engineering，2008，25(2):180－183．

［8］Yang Ke，He Xiang，Dou Litong，et al．Experimental investigation into stress-relief characteristics with upward large height and upward mining under hard thick roof［J］．International Journal of Coal Science＆Technology，2015，2(1):91－96．

［9］Xue Junhua，Wang Hanpeng，Zhou Wei，et al．Experimental research on overlying strata movement and fracture evolution in pillarless stress-relief mining［J］．International Journal of Coal Science＆Technology，2015，2(1):38－45．

［10］Hu Haifeng，Lian Xugang．Subsidence rules of underground coal mines for different soil layer thickness:Lu’an Coal Base as an example，China［J］．International Journal of Coal Science＆Technology，2015，2(3):178－185．

［11］Du Wenfeng，Peng Suping，Zhu Guowei，et al．Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining［J］．International Journal of Coal Science＆Technology，2014，1(2):184－191．

［12］何富连，赵计生，姚志昌．采场岩层控制论［M］．北京:冶金工业出版，2009．

［13］马庆云，赵晓东，宋振骐．采场老顶岩梁的超前破断与矿山压力［J］．煤炭学报，2001，26(5):473－477．Ma Qingyun，Zhao Xiaodong，Song Zhenqi．Break of main roofahead of workface and ground pressure［J］．Journal of China Coal Society，2001，26(5):473－477．

［14］朱德仁．长壁工作面老顶的破断规律及其应用［D］．徐州:中国矿业大学，1987．

［15］李猛，张吉雄，姜海强，等．固体密实充填采煤覆岩移动弹性地基薄板模型［J］．煤炭学报，2014，39(12):2369－2373．Li Meng，Zhang Jixiong，Jiang Haiqiang，et al．A thin plate on elastic foundation model of overlying strata for dense solid backfill minin［J］．Journal of China Coal Society，2014，39(12):2369－2373．

［16］王春玲，黄义．弹性地基板的分析简化模型［J］．岩土力学，2008，29(1):52－57．Wang Chunling，Huang Yi．Refined model for analysis of plates on elastic foundations［J］．Rock and Soil Mechanics，2008，29(1): 52－57．

［17］徐芝纶．弹性力学［M］．北京:高等教育出版社，2006．

［18］李星．数值分析(第5版)［M］．北京:科学出版社，2014．

［19］何红雨．有限差分法在Maltab中的应用［M］．北京:科学出版社，2002．

中图分类号:TD323

文献标志码:A

文章编号:0253－9993(2016)06－1360－09

收稿日期:2016－02－22修回日期:2016－04－24责任编辑:常琛

基金项目:国家自然科学基金资助项目(51234005，51504259);中央高校基本科研业务费专项资金资助项目(2010QZ06)

作者简介:谢生荣(1981—)，男，江苏六合人，副教授，博士。通讯作者:陈冬冬(1988—)，男，安徽宿州人，博士研究生。E－mail:chendongbcg @163．com

Analysis on thin plate model of basic roof at elastic foundation boundary(I):First breaking

XIE Sheng-rong，CHEN Dong-dong，SUN Yan-ding，GAO Ming-ming，SUN Yun-jiang，SHI Wei
(School of Resource and Safety Engineering，China University of Mining and Technology(Beijing)，Beijing100083，China)

Abstract:By establishing the basic roof mechanical model of elastic thin plate at elastic foundation boundary and using the finite difference method of partial differential equation，this paper researched the effect of the step length，elastic foundation coefficient，basic roof thickness and elastic modulus on the basic roof main bending moment and fracture positions．It is concluded that with the increase of basic roof thickness or elastic modulus，the maximum main bending moment Mzof the middle roof section increases，and the absolute maximum main bending moment Mc，Mdof roof long side and short side decrease;with the step length increasing，the Mz，Mcand Mdincrease，while the growth rate of the Mzis smaller;and when the elastic foundation coefficient increases，the Mzdecreases，while the Mcand Mdincrease．According to the breaking criterion of the main bending moment，when the step distance or elastic foundation coefficient is small，the middle of basic roof fractures first，whereas the roof long side ahead of the coal wall breaks first;if the basic roof thickness or elastic modulus is small，the long side breaks ahead of the coal wall，whereas the central fractures first．The greater the basic roof thickness or elastic modulus，the farther the pre-breaking distance of main roof;the greater the elastic foundation coefficient or step distance，the smaller pre-breaking distance of main roof．There are three types of basic roof breaking sequence:①long side-middle-short side;②long side-short side-middle; ③middle-long side-short side．

Key words:main roof;elastic foundation;first breaking;thin elastic plate;finite difference method