初探支持向量机算法在海洋站观测数据质量控制中的应用

李飞，卢勇夺，林波，陈哲，刘思晗，徐腾

（国家海洋环境预报中心，北京100081）



初探支持向量机算法在海洋站观测数据质量控制中的应用

李飞，卢勇夺，林波，陈哲，刘思晗，徐腾

（国家海洋环境预报中心，北京100081）

摘要：为了有效提高海洋观测数据的质量，初步探索引入了一种统计学习算法——支持向量域描述（SVDD）用于海洋站多要素数据质量控制，建立了一套基于SVDD的多要素数据质控方法。该方法拥有惩罚系数C、RBF核参数、质控调节因子ΔR等多个参数，利用历史样本观测数据训练构建质量控制模型，通过该模型实现海洋观测数据质量控制。本文利用真实观测数据对该方法进行了分析检验，验证了该方法能够有效分析数据质量、发现可疑数据，对提高海洋观测资料的可靠性、科学性具有一定借鉴价值。

关键词：质量控制；SVM；SVDD；海洋数据；多要素检验

1　引言

海洋观测数据是人们认识、开发与利用海洋的重要基础。海洋环境监测站，简称海洋站，其海洋观测设施能够对海温、盐度、潮位及波浪要素等进行综合观测。海洋观测数据是制作海洋预报、警报和研究海洋变化的基础资料，其质量状况直接影响着海洋预报、警报和海洋变化研究的准确性。由于海洋站观测仪器所处恶劣环境的影响以及仪器本身的不稳定性等因素，某些观测值难免存在错误或多种观测值出现原理上的矛盾，所表征的海洋状况与实际海洋状况出现一定的偏差。为了减少这些情况的出现，数据质量控制是必不可少的，其重要性也是众所周知。但当前所采用的海洋观测数据质量控制方法却比较简单，一般主要采用的有极值控制法、3-Sigma检验法、一致性检验法、狄克逊检验法等，且多为单一要素质量控制的方法［1］。

本文尝试引入了支持向量机（Support Vector Machine，SVM）［2］的变型算法—支持向量与描述（Support Vector Domain Description，SVDD）［3］算法，该算法是基于统计学习理论［4］构建，可实现多维样本空间内的学习和分类功能，它的超球面模型可应用于判决数据的可靠性。基于SVDD构建的数据质量控制系统可利用海洋历史观测资料自动学习，生成数据质量控制模型，并对新的观测数据进行诊断和分析，当发现可疑数据时将给予标注提示，为海洋预报人员与研究者提供参考。最后，本文以海洋站实际观测资料为例，分析、探讨了基于SVDD的多要素海洋站观测数据质量控制方法的可行性与优越性。

2　算法概述

SVM是一种当前流行的模式识别算法，被广泛应用于人脸识别、说话人识别、手写识别、图像识别、时间序列预测、金融工程、地球物理反演、数据挖掘等领域中［5-7］。SVDD是SVM的一种变型算法，在样本空间中对样本数据的分布规律进行学习，在样本空间中划定一个区域，并依此作为判决依据。在多要素的质量控制中，特定的几种观测要素组成一个多维样本空间，SVDD会为输入的样本计算出一个超球面的决策边界，该边界在样本空间中描述了各要素之间的关系，并将整个空间划分为两部分。一部分是边界内的空间，是接受的部分，在数据质量控制中，落在这部分空间中的样本点可以被看作正常的观测数据；另一部分则是边界外的空间，是拒绝的部分，落在这部分空间中的样本点是被质疑的观测数据。

在训练的过程中，通过控制超球的大小和形状使超球的含义不仅仅是分开两类，而且还要把球里面的样本尽量包“牢”和包“纯”，拒绝其它类样本的进入。这也就是既要求SVDD模型包含尽可能多的样本点，另一方面又要求它的半径达到最小，因为一个半径无穷大的超球面在描述要素空间分布状态时没有任何意义［8］。这样得到的质量控制模型可以尽可能多地接受正常的观测数据，并拒绝异常的数据。

基于SVDD的质量控制系统的工作流程如图1所示。

图1 SVDD的质量控制系统的工作流程

3　滑动时间窗预处理

系统训练的对象是整年的观测数据，然而各年度的气候特点不同，一年中的四季也不同。因此将全部数据进行一次训练而建出的模型是不能满足实际需求的。类似于声纹识别中短时平稳的理论，本文采取滑动时间窗的方式，将一年分为24个时间段，将各时间段分开建立相应的模型，从而提高模型在较短时间内的准确度。本文通过时间跨度为1个月的样本训练时间跨度为15 d的模型，随着窗体向右滑动训练出不同时间段的质量控制模型，如图2所示。

生成的24个质量控制模型对应着一年中24个不同的时间段，在质量控制时，系统根据被检验数据的日期，调用相应时间段的质控模型对该数据进行检测。

图2滑动时间窗示意图

4　模型构建原理

设在由N种海洋观测要素组成的N维空间中存在一组训练样本集X=，i=1，2，…，M｝，其样本i表示N种海洋要素组成的第i个样本向量。通过该样本集可以在N维空间中确定出一个半径为R，球心为的超球面。该超球面所包围的空间是样本集X 在N维要素空间中的分布范围，即有下式成立：

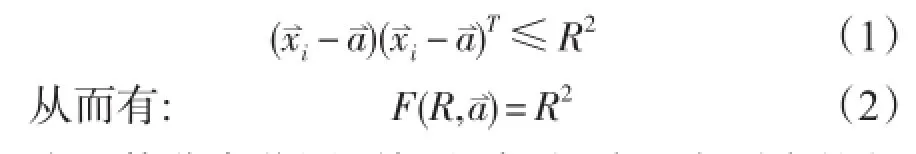
为了使分布范围更加准确，超球面应更多的包含样本向量，且更少的包含没有样本向量存在的空间，需要保证超球面的半径R最小。因此，引入拉格朗日算子，可以构建一个拉格朗日函数使上式取得最小值：

式中：拉格朗日算子αi0。对式（3）求偏导，并令其导数为0，可以得到以下条件:

将式（4）（5）带入（3）中可以得到:

通过二次规划算法得到最优的αi使式（6）最小，满足半径R最小的要求，从而更加准确的描述了样本所在的空间位置。

由于由海洋观测要素构成的训练样本质量存在不确定因素，即使经过人工检验后的样本数据也可能会有异常值的存在。从样本空间位置上看，这些异常样本往往会距离样本点聚集区域较远，若使超平面要包含所有样本点的话，势必会对空间区域描述的性能带来很大损失，影响质控模型的准确性。为了降低异常样本对质控模型的影响，需要引入松弛因子εi进入式（1）：

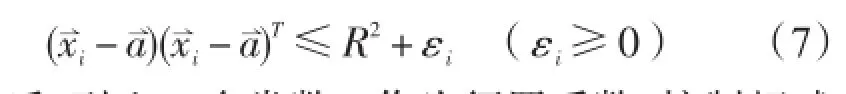
然后，引入一个常数C作为惩罚系数，控制超球面发生错误接受与错误拒绝的概率。得到下式：

上式与式（6）的形式基本一致，但是它们在二次规划优化的时候αi的取值范围是不同的。惩罚系数C表示了训练时分界面对训练样本的拒绝率。在训练样本数据经过人工质控或质量较高的情况下，训练时C的取值较小，反之C的取值较大，从而降低异常数据对模型的影响。以二维数据为例，在C比较小的情况下，落入超球面内的训练样本会比较多，反之在超球面外的样本会比较多。可以通过调整C的大小来控制质控模型误接受与误质疑的概率以满足实际的需求。

所有α≠0的样本点被称为支持向量，保留支持向量与其α值作为训练结果。因为在识别的过程中，α=0的训练样本点对于识别没有任何作用，而只会增加后续运算的计算量，对判决超平面起决定性作用的是支持向量［9］，这一点从下节式（13）中可以看出。

SVDD作为一种非标准与标准SVM一样，SVDD也可以使用不同的和函数以适应解决不同的问题。引入核函数K（x，xi）之后式（11）可化为:

图3不同惩罚系数下的超球面示意图

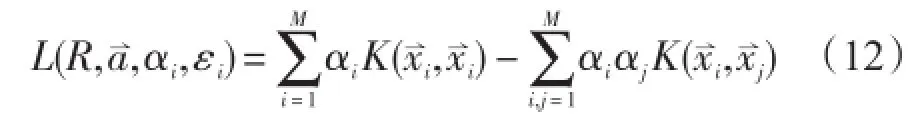
本文采用RBF非线性核函数［10］，由图4可以看出不同的非线性参数σ对超球面边界的影响。随着σ的增大，超球面的边界逐渐变得平滑，最终趋近于球面。

至此，由支持向量、拉格朗日算子αi构成的数据质量控制模型已训练完成，该模型表示了N维要素空间中观测数据样本的分布范围特点。

5　质量控制原理

在使用质控模型进行质量控制的阶段，通过下式判断一个被测样本是否位于超球面所包含的范围内，从而判断该样本是否为可疑数据。

M

通过调节ΔR的大小改变模型对可疑数据的敏感度，当被测样本点的质疑系数r满足r（R+ΔR）2时，认为该测试样本为正常数据，否则为可疑数据，交由纠错系统或人工进行处理。

图4不同参数σ对超球面边界的影响

6　算法应用分析

本文选取了小麦岛3 a的水温和气温历史数据作为训练样本。这两种要素相关性强，且要素样本空间分布受时间影响较大，便于说明算法应用过程。

在水温和气温组成的二维样本空间中，这3 a的样本在空间中的分布特征如图5所示。

在通过分时间段进行训练后，可得到各段时间所处的样本空间位置。通过训练共生成24个时间跨度为半个月的模型，如图6中红色圈出的部分所示，所圈出的部分代表了质控模型所处的空间范围。

图5水温-气温二维样本空间分布

图6　质控模型空间示意（图a—x依次分别为1月上半月至12月下半月）

在使用模型进行质控的阶段，通过待测样本点与相应时段模型所在的空间位置对比即可得到该数据的可疑程度。根据实际效果，通过调节因子ΔR改变模型对可疑数据识别的敏感度。图7中红色样本点即为可以样本。

如图7所示，随着调节因子增大，模型识别敏感度降低，系统所提示的可疑数据明显减少，在降低误质疑率的同时增大了误接受率，在实际使用中可根据不同需求设置相应的ΔR值。

由于质控功能的特殊性，无法通过观测数据自身对质控效果进行检验，本文通过人工引入随机误差的方式检验质控效果。本文从3 a的样本中随机选取了1174个已经被去除异常值的样本点，并给水温和气温要素分别引入了随机误差。通过SVDD模型进行质量控制后的结果如表1所示。

表1中误差距离表示引入误差后的样本点与原样本点在样本空间中的距离，距离越大误差约大。根据实验结果，在误差距离较小的情况下系统无法识别，这种情况在实际中一般属于各次观测的正常差异或可接受的观测误差，而随着误差距离的逐渐增加，系统发现可疑值的概率在逐步提高。

在单要素误差引入的情况下，本文对SVDD算法和3-Sigma算法进行了对比试验，针对小麦岛水温数据，从3 a的样本中随机选取了已经被去除异常值的样本点，并人工引入了随机误差。通过3-Sigma算法和SVDD算法分别进行质量控制，结果如表2所示。

表2中的误差距离即所引入的水温误差值，通过对比可以看出，在误差较小的时候，SVDD方法可识别出更多的异常值，并且在误差约为4—4.5℃的时候即可识别出90%以上异常值，而3-Sigma算法需要在6.5—7℃。

由此可见，SVDD算法在多要素的质量控制中具有较好的性能，并且其单要素的质量控制性能要明显优于3-Sigma算法。

图7调节因子ΔR对识别的影响

表1 SVDD方法多要素误差引入测试

表2 3-SIGMA方法单要素误差引入测试

表3 SVDD方法单要素误差引入测试

7　结论

本文初步探讨分析了基于SVDD算法的海洋站多要素数据质量控制方法，通过惩罚系数C、非线性核函数参数σ、调节因子ΔR的调节，实现了分析、处理及标示海洋数据质量状况的功能。验证了统计学习算法在海洋数据质量控制中使用的可行性，对提高观测资料的科学性、可靠性具有借鉴意义。海洋观测数据量庞大、要素间取值范围差异大、要素间相关程度不同等特点都会对数据质量控制模型训练的准确性带来影响，需要不断加以研究和优化。同时，统计学习算法与海洋数据质量控制都是复杂、系统的科学过程，在海洋观测数据质量控制的实际应用中仍有许多问题需要进一步研究。未来将尝试通过相关性检测和峰值检测等多种手段进一步检测可疑值，尽可能的降低误接受与误质疑率。

参考文献：

［1］陈上及，马继瑞.海洋数据处理分析方法及其应用［M］.北京:海洋出版社，1991

［2］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26（1）:32-42.

［3］Tax D M J，Duin R P W.Support vector domain description［J］. Pattern Recognition Letters，1999，20（11-13）:1191-1199.

［4］Vapnik V N.The Nature of Statistical Learning Theory［J］.IEEE Transactions on Neural Networks，1995，10（5）:988-999.

［6］杨一文，杨朝军.基于支持向量机的金融时间序列预测［J］.系统工程理论方法应用，2005，14（2）:176-181，doi:10.3969/j.issn. 1005-2542.2005.02.017.

［7］白鹏，张喜斌，张斌，等.支持向量机理论及工程应用实例［M］.西安:西安电子科技大学出版社，2008.

［8］李飞.基于支持向量机的说话人识别［D］.北京:北京信息科技大学，2012.

［9］Tax D M J，Duin R P W.Support Vector Data Description［J］. Machine Learning，2004，54（1）:45-66.

［10］Pekalska E，Paclik P，Duin R P W.A Generalized Kernel Approach to Dissimilarity-based Classification［J］.Journal of Machine Learning Research，2002，2（2）:175-211.

中图分类号：P714

文献标识码：A

文章编号：1003-0239（2016）02-0066-08

DOI:10.11737/j.issn.1003-0239.2016.02.010 ［5］祁亨年.支持向量机及其应用研究综述［J］.计算机工程，2004，30（10）:6-9，10.3969/j.issn.1000-3428.2004.10.003.

收稿日期：2015-07-16

基金项目：国家海洋局海洋公益性行业科研专项（201205006）；中国科学院海洋环流与波动重点实验室开放基金课题（KLOCAW1410）

作者简介：李飞（1987-），男，工程师，硕士，主要从事预警报视频会商系统和数据质量控制的理论和应用研究。E-mail:lif@nmefc.gov.cn

Preliminary study of marine observation data quality control based on support vector machine algorithm

LI Fei，LU Yong-duo，LIN Bo，CHEN Zhe，LIU Si-han，XU Teng
（National Marine Environment Forecasting Center，Beijing 100081 China）

Abstract：A statistical learning algorithm，supporting vector domain description（SVDD），is introduced，and a method of multi factor data quality control based on SVDD is established.Quality control model can be constructed by historical sample observation data，and the quality control of ocean observation data can be realized by the model.In this paper，the method is analyzed by real data，and proved to effectively analyze the data quality and find suspicious data.It has some reference value for improving the reliability and scientific of the marine observation data.

Key words：data quality control；SVM；SVDD；marine data；multi-element