基于模拟退火和区域划分的海表流场反演算法研究
张夏荣,黄云仙*,严卫,赵现斌
(1.解放军理工大学 气象海洋学院,江苏 南京 211101)
基于模拟退火和区域划分的海表流场反演算法研究
张夏荣1,黄云仙1*,严卫1,赵现斌1
(1.解放军理工大学 气象海洋学院,江苏 南京 211101)
摘要:经典的海洋表面流场迭代反演算法采用固定的校正系数对探测区域进行整体分析和计算,因此耗时较长且反演精度也受到了一定程度的限制。本文提出利用模拟退火算法对反演过程中的校正系数进行优化,使其能根据每一次反演的结果进行自适应的调整和改变,从而减少迭代次数;同时根据流场分布的特点,提出划分探测区域的反演方法,最终,在经典算法的基础上给出了改进的海表流场反演算法。仿真反演实验结果表明,改进后的反演算法,其时效性和精度都有了明显提高。
关键词:顺轨干涉SAR;海洋表面流场;M4S模型;模拟退火算法
1引言
海洋表面流场是一种重要的海洋动力学现象,无论是在输送海洋热量、盐度等[1]方面,还是对研究海洋、陆地和大气之间的相互作用[2]以及海洋灾害预警方面都具有十分重大的科学意义[3]。
目前针对海表流场的测量方法主要有两大类,分别为传统手段测量和遥感测量。其中传统的海流测量包括浮标和电磁式海流计等[4],主要存在采样点少、成本较高的问题;而通过遥感手段虽然可以获取空间覆盖范围较广的海表流场数据,但无论是星载高度计还是合成孔径雷达(Synthetic Aperture Radar,SAR)都有各自的局限性[5—6]。其中星载高度计由于受星下点观测几何的限制,其获得的流场距离向分辨率较为粗糙,约为几十到几百千米量级;而合成孔径雷达的强度图像并不能直接反映流场速度的变化,且其在成像过程中存在多种非线性调制机制[7],这也增大了流场反演的难度。
顺轨干涉SAR(Along-Track Interferometric SAR,ATI-SAR)是1987年由美国Goldstein和Zebker首先提出来的一种技术,其探测的干涉相位与表面流场的径向速度分量成正比,据此可以反演高分辨率的海表流场信息[8—9]。基于M4S微波成像仿真模型,Romeiser等[10—12]提出了顺轨干涉SAR流场迭代反演算法,于祥祯等[13]给出了详细的海表流场迭代校正方案,并利用美国喷气推进实验室JPL(Jet Propulsion Laboratory)的机载SAR数据开展了反演实验,验证了反演方法的有效性。但是,该反演算法对于校正系数的选取未作详细的说明,而合理选择校正系数可以减少迭代次数,缩短M4S模型仿真计算的时长,从而提高反演速度。另外,在计算过程中,当目标区域的海表流场变化较大时,利用该算法反演的流场与真实流场存在较大的误差。本文拟在该经典的反演算法基础上,对校正算法进行优化,从而有效提高全局流场的反演精度并缩短整个反演过程的计算时间。
2经典的海表流场反演算法
2.1M4S微波成像仿真模型
M4S模型是一个可以仿真计算海表流场、海面风场以及海浪等海洋活动的工具包[14],它由汉堡大学的Roland Romeiser开发并首次应用于海表流场的仿真和反演。
M4S模型主要包括M4Sw320、M4Sr320和M4Sq320等计算模块。其中,M4Sw320为海浪谱计算模块,用于计算给定海面风场、海表流场条件下海面微尺度波的波高谱;M4Sr320为雷达成像计算模块,利用生成的海浪谱,以及设置的雷达参数和平台参数等计算多普勒谱、SAR强度和干涉相位图像;M4Sq320为单点计算模块,计算单点雷达散射信号或者多普勒谱。
采用M4S模型开展海表流场反演研究时,给定海面风场、海表流场、雷达参数和平台参数,可以计算顺轨干涉SAR的强度和干涉相位图像,M4S模型仿真计算的主要流程如图1所示。
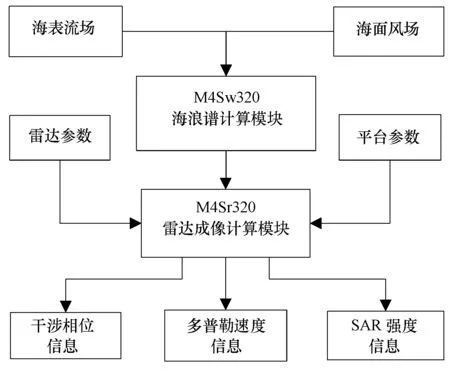
图1 M4S模型计算流程图Fig.1 The flow chart of M4S model
2.2经典海表流场迭代反演算法
基于M4S模型,Romeriser和Hartmut[9]提出了顺轨干涉SAR海表流场迭代反演算法,于祥祯等[7,13]给出了具体的海表流场校正方案,如图2所示。
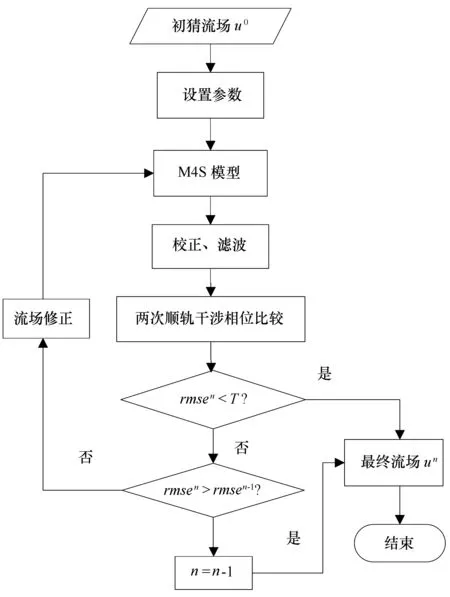
图2 经典的海表流场迭代反演算法流程图[7,13]Fig.2 Classical iterative inversion algorithm flow chart of the ocean surface current[7,13]
图2中,un表示最终反演流场,n表示迭代次数,T表示顺轨干涉相位的均方根误差阈值。u0代表初猜流场,通过式(1)确定:
(1)
式中,λ表示雷达波长,V表示平台飞行速度,L表示有效基线长度,θ表示雷达入射角,φ0表示实测顺轨干涉相位。
具体流程为:
(1)首先,利用式(1)通过实测顺轨干涉相位计算得到初猜流场u0。
(2)初始化海表流场迭代反演所涉及的参数。
(3)将风场以及得到的海表流场、平台参数、雷达参数等输入M4S模型,计算顺轨干涉相位图像。
(4)由于流场方位向梯度的存在[7,13],需对得到的干涉相位图像进行方向偏移的校正和均值滤波处理。
(5)然后将仿真的干涉相位图像与实际干涉相位图像进行对比,如果干涉相位的均方根误差rmsen
(6)将仿真和实际的干涉相位进行逐个比对,通过设置合理的校正系数对干涉相位偏差大于阈值T的相位对应的流场值进行修正,将修正后的流场重新输入M4S模型,进行下一次迭代校正。
通过实际的迭代计算发现,该方法虽能够有效的反演出海表流场,但是其对流场校正系数所涉及的比例因子始终设置为一个固定值,这样就不能很好的根据流场迭代的次数和当前精度实现系数的自适应调整,从而减缓了迭代的收敛速度。另外,算法针对的是目标区域所有的干涉相位值和流场值,没有考虑到各区域流场的大小和方向不同时对校正系数有不同的要求,这也会影响海表流场反演的精度。
因此,本文在该算法的基础上,针对校正系数和区域划分,开展两个方面的研究和改进。
3改进的海表流场反演算法
3.1基于模拟退火算法优化校正系数
模拟退火算法(Simulated Annealing,SA)的思想最早是由Metropolis于1953年提出的[15],它来源于固体退火降温的原理,即将固体加温至充分高,再让其慢慢冷却这一过程。该过程可以解释为:当对固体加热时,其内部粒子的热运动剧烈程度会随温度的增大而增大,此时粒子呈现出无序状,内能也随之增大;若停止加热,则固体内部粒子会随温度的降低逐渐趋于有序,其热运动的剧烈程度也逐渐降低,最后在常温时达到基态,此时内能减为最小[16]。模拟退火算法在实际应用中的基本思路是:首先在高温下进行搜索,由于这个时候各个状态出现的几率相差不大,可通过粗搜索大致找到低能区域;随着温度的降低,各状态出现概率的差距逐渐拉大,搜索精度也不断提高,进而越来越准确的找到目标函数的全局极小点,也即问题的最优解[17]。
要将模拟退火算法具体应用到流场的校正过程中,需要找到合适的参量来代替固体退火降温这一过程中的内能和温度。本文用目标函数值代替固体退火过程中的内能,用校正系数中的比例因子β代替固体退火过程中的温度。具体思路为:首先,根据校正区域的流场特点给定一个初始的比例因子β0,并在其邻域中随机产生一个新的值;然后拟定一个接受准则,该准则具有一定容错性,即允许目标函数在一定范围ζ内接受使目标函数恶化的β,算法持续进行“产生新β值—计算目标函数值—判断是否接受新的β—接受或舍弃”的迭代过程[16]。经过多次β值的变化后,可以求得流场校正问题的相对最优解。接着,逐步减小比例因子β的变化范围,重复执行上述迭代过程,当这个范围趋于零时,系统也越来越趋于平衡状态,也即反演流场趋于最优流场,此时停止迭代并输出该流场,如图3所示。
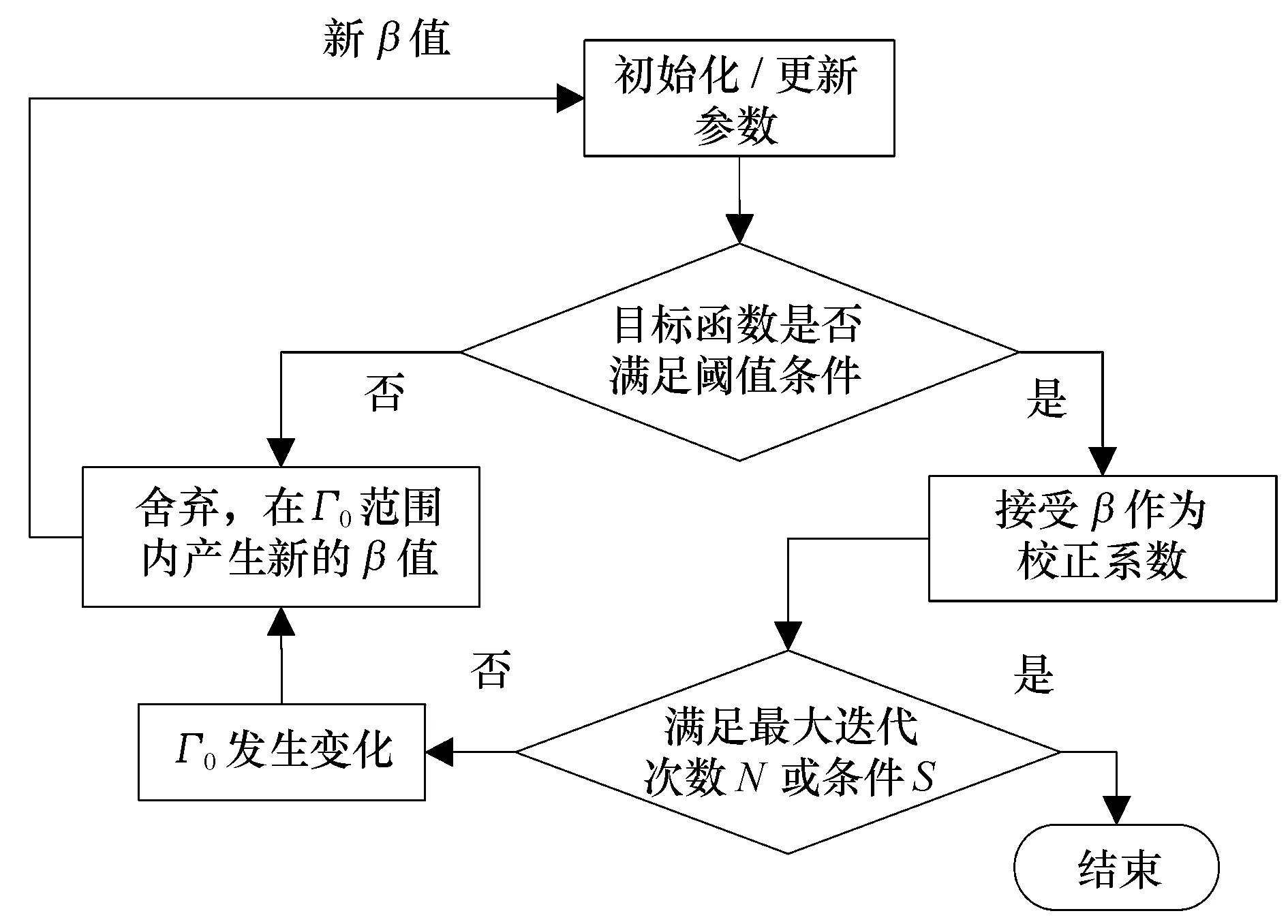
图3 基于模拟退火算法优化校正系数流程图Fig.3 The flow chart of optimizing correction factor based on simulated annealing algorithm
具体步骤如下:
(2)
(3)
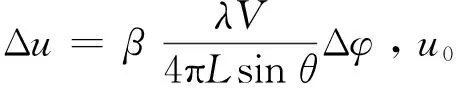
(2)初始化参数。除了给定初始的比例因子β0以外,还包括比例因子的变化范围Γ0([-x0,x0])、衰减因子τ(负值)、最大迭代次数N、终止条件S和目标函数可以接受的范围ζ(包括ζ1和ζ2)。
(3)判断是否接受新的β值。当目标函数满足下面的任意一个条件时,接受此时的β值;否则,舍弃该β值并在变化范围Γ0内随机产生新的β并重新进行判断。
(4)
(5)
(4)如果满足终止条件S或达到最大迭代次数N,则迭代终止;否则,令x0=x0+τ,并重复步骤(3)。其中终止条件S为同时满足式(4)和式(5)。
3.2探测区域划分的流场优化方案
在进行流场迭代校正前,根据流场大小和方向的不同,将目标区域进行划分,结合前文提出的优化校正系数的思想,对每一块区域分别进行迭代计算,最后再将各区域的输出流场合成为最终输出流场,如图4所示。
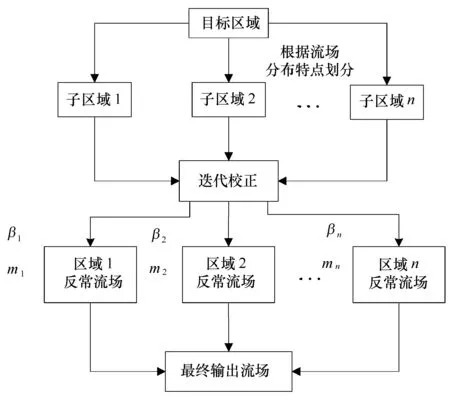
图4 划分探测区域的流场校正方案Fig.4 Current correction scheme for the division of detection area
在对目标区域进行划分时,主要涉及到流向和流速两个参量,风场的信息未作考虑。
由试验结果可知,脆口萝卜的各包装材质产品在各温度梯度储存期间理化指标pH和总酸都基本稳定,产品中细菌总数均<10 cfu/g,符合产品设计标准,但是随着产品储存期的延长,产品的色泽、香气、口感都呈下降趋势,通过Q10方法测算同种包装材质,不同储存温度影响产品货架期,高温缩短了产品货架期;不同种类的包装材质对脆口萝卜产品货架期影响很大,铝箔袋产品能够达到324天,镀铝袋产品229天,透明袋产品最少,只有95天。不同的包装材质,脆口萝卜货架期差异大,与包装材质的氧气透过率、吸湿性以及产品配料特性有关。
如图5所示,将目标区域根据流场分布特点[18]划分为9块区域(这里为方便说明,将其等分,实际计算过程中并非完全均等划分),每块区域的流场大小和方向阈值依具体的流向和流速确定(实验中以流速差的绝对值不大于0.5 m/s,流向差的绝对值不大于6°为划分标准)。

图5 对目标区域进行划分Fig.5 Division of detection area
3.3改进的海表流场反演算法
在经典的海表流场反演算法基础上,作上述两处优化,从而得到了改进后的海表流场反演算法,如图6所示。具体步骤如下:
(1)首先利用式(1)通过实测顺轨干涉相位计算得到初猜流场u0。
(2)根据划分标准将探测区域划分为若干个子区域并对每一个子区域进行下面的反演迭代。
(3)输入风场、平台参数和雷达参数等,进行海表流场的迭代反演。
(4)将仿真的干涉相位图像与实际干涉相位图像进行对比,如果干涉相位的均方根误差rmsen
(5)将仿真和实际的干涉相位进行逐个比对,在对校正系数进行优化的基础上,修正干涉相位偏差大于阈值T的相位对应的流场值,将修正后的流场重新输入M4S模型,进行下一次迭代校正。
(6)将得到的每一个子区域的“最优流场”进行合成,得到最终的反演流场。
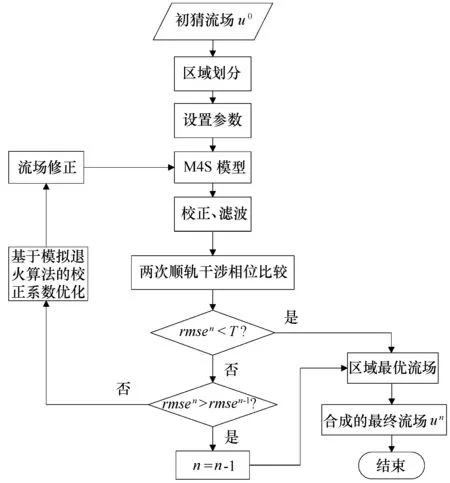
图6 改进后的顺轨干涉SAR海表流场迭代反演算法Fig.6 Improved iterative inversion algorithm flow chart of the ocean surface current
4结果与分析
4.1仿真数据及实验
为了验证改进后算法的性能,进行如下仿真和反演实验。
首先,模拟一个二维海表流场(100×100,空间间隔为50 m)作为“真实流场”,海面背景风向为35°,风速为3 m/s。为了获取二维的海表流场,假设星载SAR(右侧视)沿垂直方向探测(按照雷达视向分别记为x和y方向),探测方案如图7所示,红色箭头表示海表流场。

图7 海表流场及星载SAR探测方案Fig.7 Ocean surface current and space-borne SAR detection scheme
设置基于星载顺轨干涉SAR的参数,包括中心频率、雷达波长、极化方式、雷达入射角、飞行高度和速度、有效基线长度等,如表1所示。
然后,利用M4S模型计算初始相位φ0,假设其为“真实相位”(实际探测中,初始相位应为干涉SAR实测结果),M4S模型计算的顺轨干涉相位图像如图8所示。接着,利用式(1),通过初始相位φ0计算初猜流场u0,并分别利用经典算法和本文改进的海表流场反演算法反演流场。最后,将反演流场与模拟的海表流场(真实流场)进行比对,并对两种反演算法进行分析。

表1 星载顺轨干涉SAR参数设置
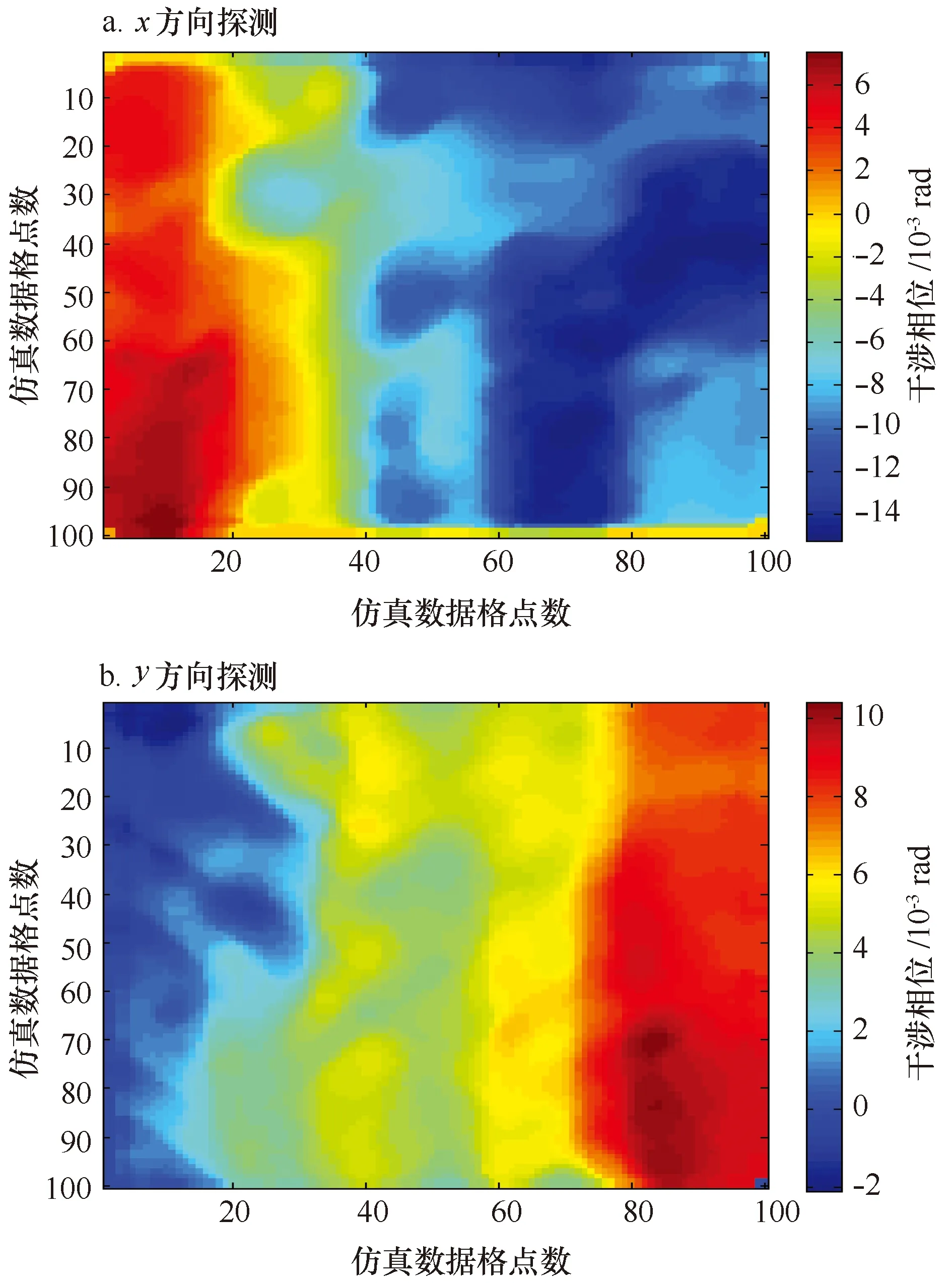
图8 M4S模型计算的初始顺轨干涉相位Fig.8 The initial phase of along-track interferometric SAR calculated by M4S model
4.2反演结果分析
经过计算,海表流场的反演结果如图9、图10和图11所示。其中,图9描述了反演流场与给定流场(真实流场)的比对分析情况,图10a和b分别描述了经典算法和改进后算法海表流速的反演结果与真实值比对分析情况,而图11a和b则分别描述了经典算法和改进后算法海表流向的反演结果与真实值比对分析情况。
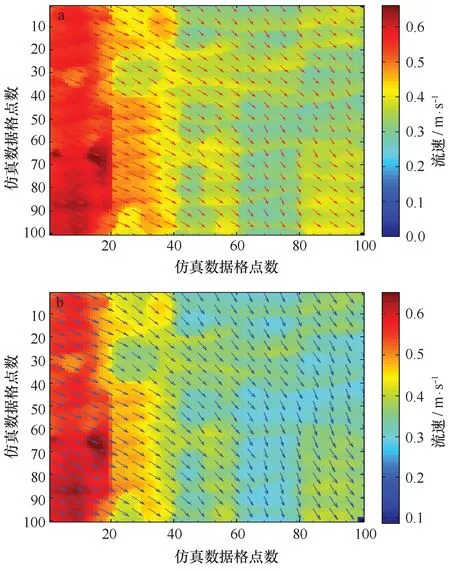
图9 反演流场(a)与真实流场(b)Fig.9 Inversion of flow field (a) and real flow field (b)
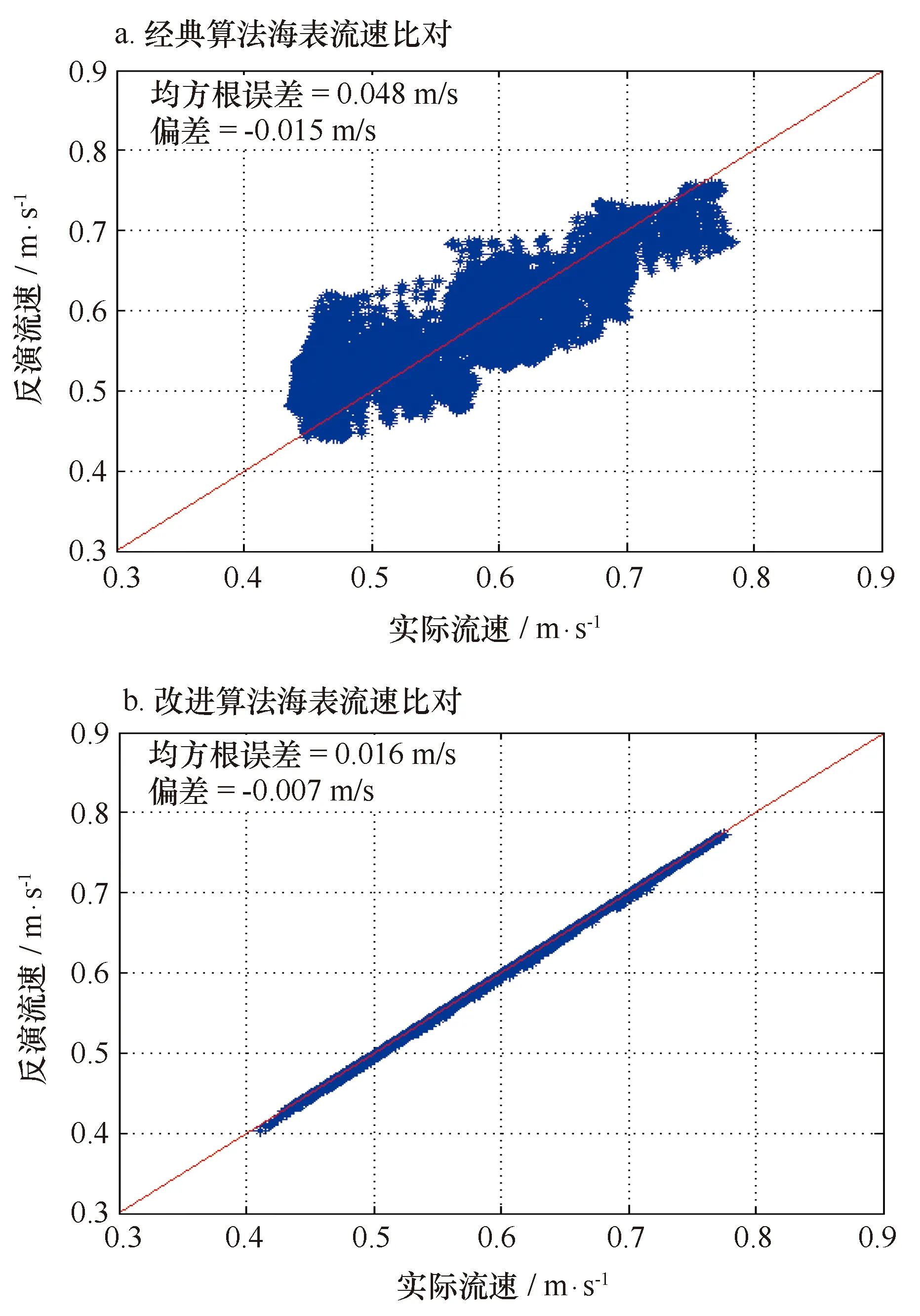
图10 经典算法(a)和改进算法(b)的海表流速反演值与真实值比对分析情况Fig.10 Sea surface velocity inversion and real value analy-sis of classical algorithm (a) and improved algorithm (b)
从图10可知,经典算法海表流速反演结果的均方根误差为0.048 m/s,偏差为-0.015 m/s;改进算法的海表流速反演结果的均方根误差为0.016 m/s,偏差为-0.007 m/s。
从图11可知,经典算法海表流向反演结果的均方根误差为4.616°,偏差为1.670°;改进算法的海表流向反演结果的均方根误差为0.486°,偏差为-0.334°。
分析反演结果可知,改进后的算法较经典算法在流场速度的精度上有较大提高,且反演流场与真实流场的符合程度也更高。其中,海表流速的均方根误差优于0.02 m/s;海表流向的均方根误差优于1.0°。
此外,采用经典海表流场反演算法反演海表流场时,迭代次数通常为6~8次,而采用模拟退火算法优化校正系数后,通常迭代2~3次。因此,改进的海表流场反演算法也加快了海表流场的收敛速度,减少了处理时间。
5小结
本文首先详细介绍了于祥祯等提出的顺轨干涉SAR海洋表面流场迭代反演算法,并简要的分析了该方法存在的不足。然后针对这些不足给出了基于模拟退火算法优化校正系数的具体流程和区域划分的流场优化方案。经过实验对比分析可以看出,改进后的流场迭代反演算法较经典的反演算法在迭代的收敛速度和反演的精度上都有所提高,其中本次实验的迭代次数较之前减少了约65%,流速和流向的偏差较之前分别减少了约53%和79%,证明该改进算法可行有效。
随着顺轨干涉SAR海洋观测数据的积累以及利用M4S模型反演海表流场算法研究的深入,海洋表面流场的测量精度将进一步提高,这对监测海流和通过海流计算其他海洋参量如海浪谱等具有重要意义。
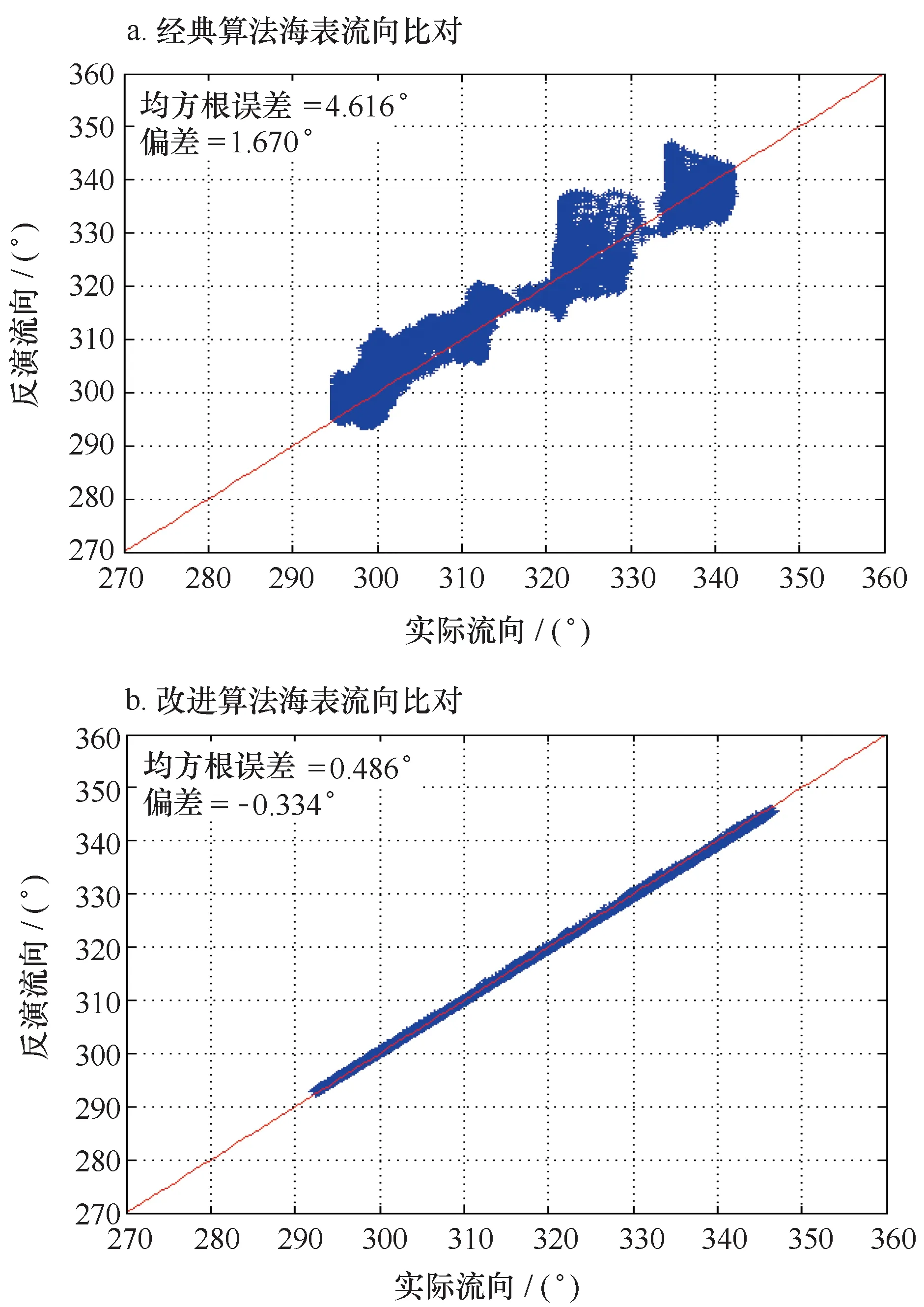
图11 经典算法(a)和改进算法(b)的海表流向反演值与真实值比对分析情况Fig.11 Sea surface flow direction and real value analysis of classical algorithm (a) and improved algorithm (b)
参考文献:
[1]刘巍, 张韧, 王辉赞,等. 基于卫星遥感资料的海洋表层流场反演与估算[J]. 地球物理学进展, 2012, 27(5): 1-4.
Liu Wei, Zhang Ren, Wang Huizan, et al. Sea surface flow field retrieval and estimation based on satellite remote sensing data[J]. Progress in Geophysics,2012,27(5):1-4.
[2]冯贵平, 金双根, Jose M,等. 利用卫星测高、GRACE和GOCE资料估计全球海洋表面地转流[J]. 海洋学报, 2014, 36(9):45-55.
Feng Guiping, Jin Shuanggen, Jose M, et al. Global ocean surface geostrophic currents estimated from satellite altimetry, GRACE and GOCE[J]. Haiyang Xuebao, 2014,36(9):45-55.
[3]常亮, 高郭平, 郭立新. 星载SAR海洋表层流场反演综述[J]. 海洋科学进展, 2015(1):1-4.
Chang Liang, Gao Guoping, Guo Lixin. Review on ocean surface current field measurement by space-borne SAR[J]. Advances in Marine Science,2015(1):1-4.
[4]陈大可, 许建平, 马继瑞,等. 全球实时海洋观测网(Argo)与上层海洋结构、变异及预测研究[J]. 地球科学进展, 2008, 23(1):1-7.
Chen Dake, Xu Jianping, Ma Jirui, et al. Argo global observation network and studies of upper ocean structure, variability and predictability[J]. Advances in Earth Science,2008,23(1):1-7.
[5]Paduan J, O’Donnell J, Allen A, et al. Surface current mapping in U.S. coastal waters: Implementation of a national system[R]. Arlington: Ocean, US, 2004.
[6]Barrick D E,Evans M W,Weber B L. Ocean surface current mapped by radar[J]. Science, 1977, 198(4313):138-144.
[7]于祥祯. 顺轨干涉SAR对海洋表面流场监测的若干问题研究[D]. 北京:中国科学院研究生院, 2012.
Yu Xiangzhen. Study on some problems of ocean surface current observation by along-track interferometric SAR[D]. Beijing:Graduate University of Chinese Academy of Sciences,2012.
[8]Goldstein R M, Zebker H A. Interferometric radar measurement of ocean surface currents[J]. Nature, 1987, 328(6132):707-709.
[9]Romeiser R, Hartmut R. Theoretical evalution of several possible along-track InSAR modes of Terra SAR-X for ocean current measurements[J]. IEEE Trans Geosci Remote Sens, 2007, 45(1):21-35.
[10]Romeiser R. Current measurements by airborne along-track InSAR: measuring technique and experimental results[J]. IEEE Journal of Oceanic Engineering, 2005, 30(3):552-569.
[11]Romeiser R, Schwabish M, Schulz-Stellenfleth J, et al. Study on concepts for radar interferometric from satellites for ocean (and land) applications (KoRIOLiS)[R].Germany:University of Hamburg, 2002.
[12]Romeiser R, Suchandt S, Runge H, et al. First analysis of TerrSAR-X along-track InSAR-derived currents fields[J]. IEEE Trans Geosci Remote Sens, 2010, 48(2):820-829.
[13]于祥祯, 种劲松, 洪文. 顺轨干涉SAR海洋表面流场迭代反演算法[J]. 电子与信息学报, 2012(11):2660-2665.
Yu Xiangzhen, Zhong Jinsong, Hong Wen. An iterative method for ocean surface current retrieval by along-track interferometric SAR[J].Journal of Electronics and Information Technology, 2012(11):2660-2665.
[14]Romeiser R. M4S 3.2.0 user’s manual[S].Germany:University of Hambury, 2008.
[15]Metropolis N, Rosenbluth A W, Rosenbluth M N, et al.Equation of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 56(21):1087-1092.
[16]庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D]. 长春:吉林大学, 2006.
Pang Feng. The principle of SA algorithm and algorithm’s application on optimization problem[D]. Changchun:Jilin University,2006.
[17]朱凯. 精通MATLAB神经网络[M]. 北京:电子工业出版社, 2010.
Zhu Kai. Proficient in MATLAB neural network[M]. Beijing:Publishing House of Electronics Industry, 2010.
[18]陈丽娜. 基于海洋流场的拓扑区域划分的研究[J]. 电子设计工程, 2011(8): 10-12.
Chen Li’na. Research on topological region division based on ocean flow field[J]. Electronic Design Engineering, 2011(8): 10-12.
A study of ocean surface current inversion algorithm based on simulated annealing and region partition
Zhang Xiarong1,Huang Yunxian1,Yan Wei1,Zhao Xianbin1
(1.InstituteofMeteorologyandOceanography,PLAUniversityofScienceandTechnology,Nanjing211101,China)
Abstract:The classical ocean surface current iterative inversion algorithm used constant correction factor to analyze and calculate the whole detection area, so it is time-consuming and the accuracy is limited. In order to improve the efficiency and accuracy of the inversion calculation, this paper used simulated annealing algorithm to optimize the correction coefficient, which can be adaptively changed according to the result of each inversion. Moreover, detection region was divided according to the characteristics of the current distribution. Finally, a modified ocean surface current inversion algorithm is proposed based on the classical method. The simulation results show that the efficiency and accuracy of the improved inversion algorithm are obviously improved.
Key words:Along-Track Interferometric SAR; ATI-SAR; Ocean surface current; M4S model; simulated annealing algorithm
收稿日期:2015-08-17;
修订日期:2016-04-05。
基金项目:国家自然科学基金面上项目(41375029,41575028);国家自然科学基金青年基金项目(41505016);装备预研共用技术基金(9140A21070114JB25344)。
作者简介:张夏荣(1991—),男,甘肃省定西市人,研究方向为微波海洋遥感。 *通信作者:黄云仙,女,上海市人,副教授,从事气象信息处理技术研究。E-mail:gsdxzxr@163.com
中图分类号:P731.21
文献标志码:A
文章编号:0253-4193(2016)07-0014-08
张夏荣,黄云仙,严卫,等. 基于模拟退火和区域划分的海表流场反演算法研究[J]. 海洋学报, 2016, 38(7): 14-21, doi:10.3969/j.issn.0253-4193.2016.07.002
Zhang Xiarong, Huang Yunxian, Yan Wei, et al. A study of ocean surface current inversion algorithm based on simulated annealing and region partition[J]. Haiyang Xuebao, 2016, 38(7): 14-21, doi:10.3969/j.issn.0253-4193.2016.07.002

