缺陷深度对低频交流励磁检测结果的影响
陆新元李光海杨剑锋
(1.北京化工大学 北京 100029)(2.中国特种设备检测研究院 北京 100029)
缺陷深度对低频交流励磁检测结果的影响
陆新元1李光海2杨剑锋1
(1.北京化工大学 北京 100029)
(2.中国特种设备检测研究院 北京 100029)
摘 要:文章针对承压设备常用铁磁性材料的腐蚀缺陷,进行了低频交流励磁检测方法的仿真和试验。基于低频交流励磁方法的仿真模型,分别研究了腐蚀缺陷位于上下表面时,缺陷深度变化对检测结果的影响。研究得出了磁场的幅值与相位值随缺陷深度的变化规律并进行了试验验证。结果表明,仿真结果与试验结果趋势相符。
关键词:低频交流励磁 无损检测 有限元仿真 最小二乘拟合
低频交流励磁检测技术是一种快速电磁无损检测新技术[1],一般采用低于100Hz的交流电流激励,用磁敏元件或是线圈接收磁场信号。与传统漏磁检测方法采用的直流激励相比,交流激励的磁化方式具有剩磁小、检测设备体积小、重量轻和电量消耗小等优点,可以降低检测人员的劳动强度。较低的激励频率能够增加交变磁场的渗透深度,适用于管壁较厚或带有外包覆层的不同设备的检测。同时,与直流激励得到的检测信号相比,低频交流励磁检测的信号不仅包含有幅值信息,还包含有相位信息,更有利于缺陷的判识。
1 低频交流励磁检测原理
低频交流励磁检测系统由电磁激励部分和信号拾取部分构成。一般采用绕制线圈作为激励部分,检测时,励磁线圈中施加低频的正弦电流(一般为5Hz~100Hz),产生一定强度的交变磁化场,在被测试件形成磁回路[2]。当被测试件中无缺陷时,磁力线均匀、连续地通过;当被测试件中存在裂纹等缺陷时,磁路中的磁阻增大,缺陷附近的磁场产生泄漏,磁力线发生弯曲,部分磁力线从试件泄漏到空气中,被信号拾取元件接收。
2 低频交流励磁方法仿真研究
2.1 仿真模型设计
深度是综合判断缺陷影响的重要因素之一,本文对碳钢材料中不同深度孔型缺陷进行了仿真研究。
建立的低频交流励磁检测的二维简化模型如图1所示。该二维模型主要包括低频交流励磁检测传感器和待测试件两部分。其中,传感器的激励部分主要由激励线圈和U型磁芯组成,磁敏元件在磁轭中央拾取空间中的漏磁信号,模型的主要参数见表1。笔者分别对直径为5mm,深度分别为1.2mm,2.4mm,4.8mm,6.0mm,7.2mm以及9.6mm的孔型缺陷直径剖面周围磁场进行数值计算。仿真时,以缺陷中心为坐标原点,磁轭与线圈组成的传感器以1mm为步长,经过缺陷中心及其左右各15mm的距离。磁敏元件位于磁轭中心,距钢板表面距离为1mm,用于接收空间的漏磁场。
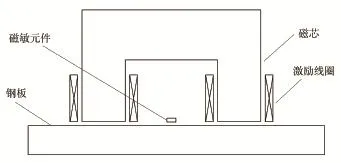
图1 仿真模型示意图
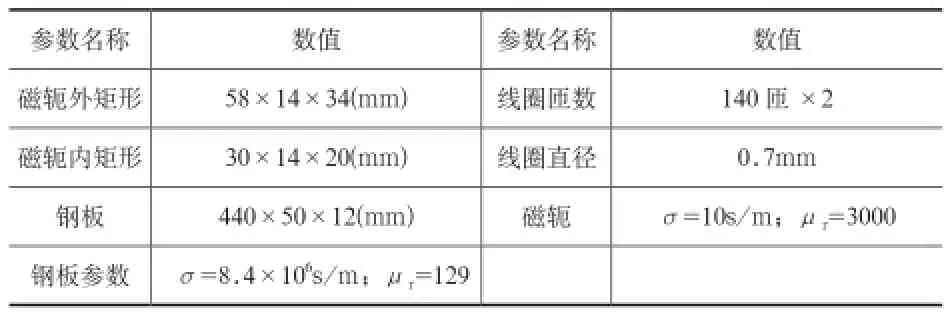
表1 仿真模型参数表
2.2 激励参数的选取
缺陷处的磁场信号主要受试件材料、外加电场、缺陷位置和形状等因素的影响。由于被测试件的材料及缺陷位置已经确定,因此,磁场信号的强弱主要取决于所施加的激励参数,即线圈匝数、激励电流强度和频率。综合考虑实际实验仪器的额定电流和线圈发热情况,激励电流选为2A。在激励电流确定的情况下,励磁频率主要影响漏磁场强度及穿透深度。
常规电磁检测中,趋肤深度与被检测材料电导率、磁导率以及激励频率相关。在材料一定的情况下,趋肤深度随着检测频率的降低而增大,其值为:

式中:
δ——趋肤深度;
ω——信号角频率;
μ——金属导体的磁导率;
σ——金属导体的电导率。
吴德会[3]等人通过实验与仿真对交流励磁方法的趋肤深度进行了探究,论证了在交流漏磁检测中趋肤效应确实存在。保持励磁强度不变而提高励磁频率的情况下,磁化场的渗透深度逐渐变浅,从而造成被测钢板表层局部磁化强度增大。基于以上仿真模型,在不同励磁频率下在直径为5m,深度为6mm的缺陷处进行数值仿真,提取裂纹上方1mm处的磁场信号的幅值,得到如图2所示的磁场空间分布图。

图2 磁场分量的扫频图
由图2可以看出,随着激励频率的增加,磁场分量幅值逐渐增加。取不同激励频率下幅值的峰值,做出趋势图如3所示。
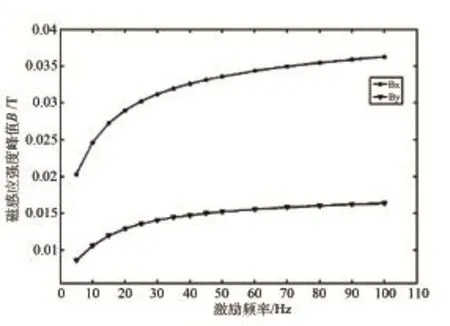
图3 不同激励频率下与磁场幅值的峰值
由图3可以看出,随着激励频率的增加,漏磁场的幅值逐渐变大并趋于平稳,即随着频率的增加,渗透深度逐渐减弱。仿真与实验均采用厚度为12mm的钢板,为了实现一定的检测深度,笔者选取仿真与实验的激励频率为10Hz。
2.3 仿真信号处理方法
最小二乘法增加了误差平方和项,能够最大限度地逼近任意非线性函数,拟合精度高。通过正弦曲线最小二乘法拟合检测信号,可以较为准确提取出低频交流励磁检测信号的幅值和相位信息,以便检测出缺陷[4,5]。
设接收线圈检测信号经放大滤波得到的正弦信号为:

ω为激励角频率,在低频交流励磁检测中,励磁信号与检测得到的漏磁信号为同频的正弦信号。φ为相位差,C为检测信号叠加的直流参数。上式在分析计算中由于φ的存在会显得比较繁杂,可将式(2)表述为:
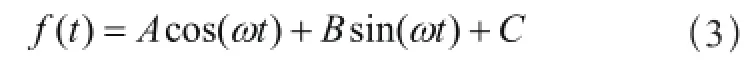
此时,相位差φ的信息包含在参数A和B中。在实际应用中,系统所得到的检测信号为离散的正弦信号,外加由电磁干扰所带来的随机误差,式(3)可表述成:

式(4)中,yn为实际系统采样得到的第n个检测信号磁场值,εn为第n个采样点的拟合误差。设系统在一个激励周期内采样N个点用于正弦曲线拟合,则基于最小二乘法得到的拟合误差平方和为:

当ε对参数A、B以及C的偏导数为0时,即求其极小值:

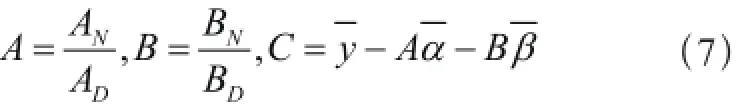
A、B、C即为正弦曲线最小二乘拟合值。由于激励信号的频率已知,因此该算法变为三参数正弦曲线拟合,在得到A、B、C参数值之后,可以得到信号的相位与幅值。
2.4 仿真结果
采用最小二乘拟合,计算得到了不同深度缺陷位于钢板上下表面时的漏磁场分量Bx和By的幅值与相位,结果如图4所示。

图4 上表面切向磁场分量随缺陷深度变化分布
由图4(a)为裂纹位于钢板上表面时,不同深度的缺陷产生的磁场信号的切向分量的幅值空间分布。从图中可以看出,缺陷深度变化对磁场信号切向分量的幅值特征参数有明显的影响。不同深度缺陷产生漏磁信号切向分量的幅值在裂纹宽度范围内呈单峰凸起,幅值信号的峰宽近似为缺陷宽度。且由趋势图5(a)看出,其峰值随缺陷深度增加呈近似线性增加趋势。经过计算得到,缺陷深度变化对漏磁信号切向磁场分量的相位特征参数同样有一定影响,不同深度缺陷产生漏磁信号切向分量的相位分布与幅值分布具有相似性,即在裂纹宽度范围内呈单峰凸起,且其峰值随缺陷深度增加而增大,趋势如图5(b)所示。

图5上表面缺陷切向磁场分量随缺陷深度变化趋势
图6为缺陷位于试件上表面时,不同深度的缺陷产生的漏磁信号法向分量的幅值和相位的空间分布。从图6(a)中可以看出,不同深度缺陷产生漏磁信号法向分量的幅值在缺陷宽度范围内N字型分布,且其峰值随缺陷深度增加而增加,其增加趋势如图7所示。由图6(b)可以看出,计算得到的法向磁感应强度的相位呈现单峰向下凹陷,但其峰值的变化规律不明显,不能够用标定等方法表征缺陷深度变化。
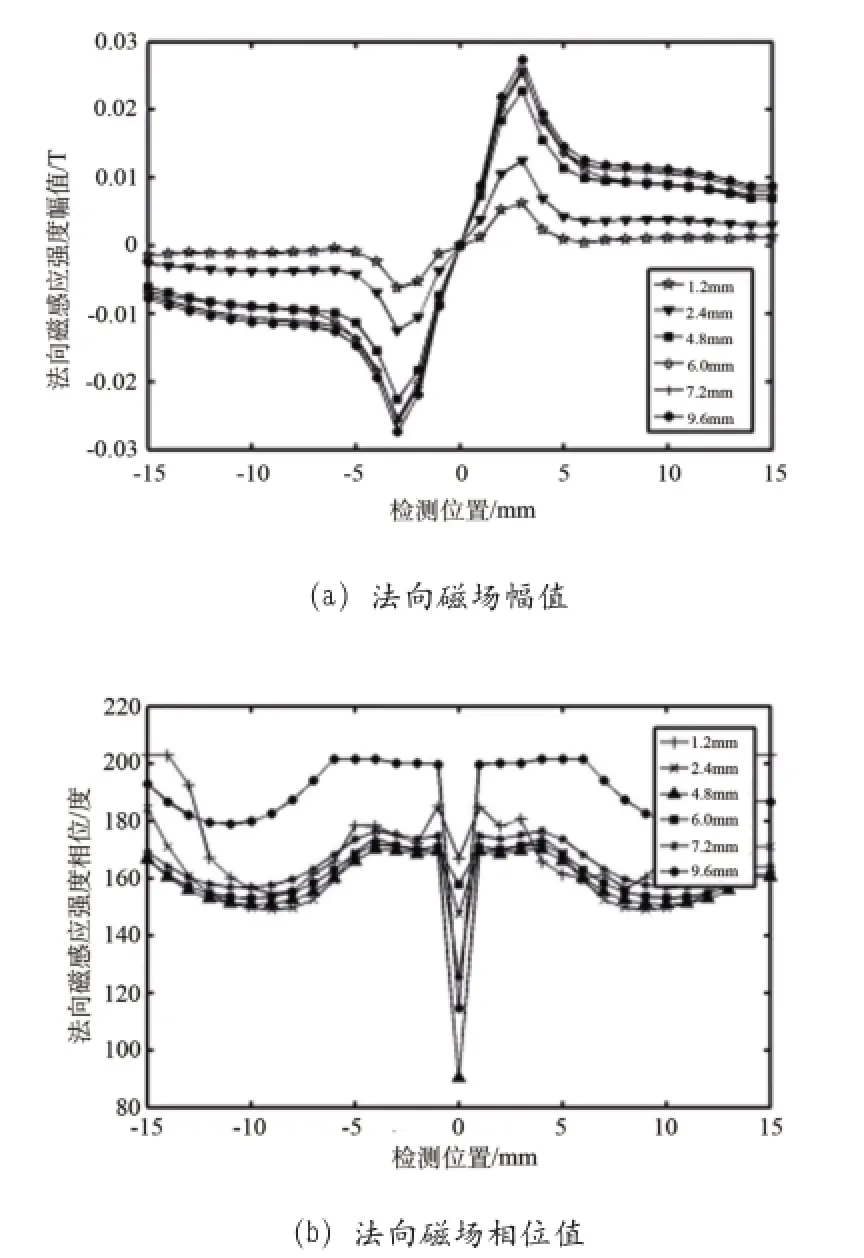
图6 上表面法向磁场分量随缺陷深度变化分布

图7 法向磁场幅值随缺陷深度变化趋势
缺陷位于钢板下表面时的检测结果如下图8所示,由图8(a)可以看出,下表面缺陷切向磁感应强度的幅值与上表面时的形状相似,同样是呈单峰凸起,但是凸起方向向下,且变化趋势近似线性。因此,结合最小二乘计算方法,可以通过缺陷信号的切向磁感应强度幅值波峰凸起方向区分缺陷位于上表面还是下表面。当缺陷深度为1.2mm与2.4mm时,幅值检测结果不明显,但是随着缺陷深度的增加,幅值逐渐增大,其趋势如图9(a)所示。由图8(b)的下表面切向磁场相位图可以看出,缺陷为1.2mm,2.4mm与4.8mm时,相位信号波形不明显,几乎呈现一条直线。但是同样,随着缺陷深度的增加,幅值逐渐增大,其趋势如图9(b)所示。
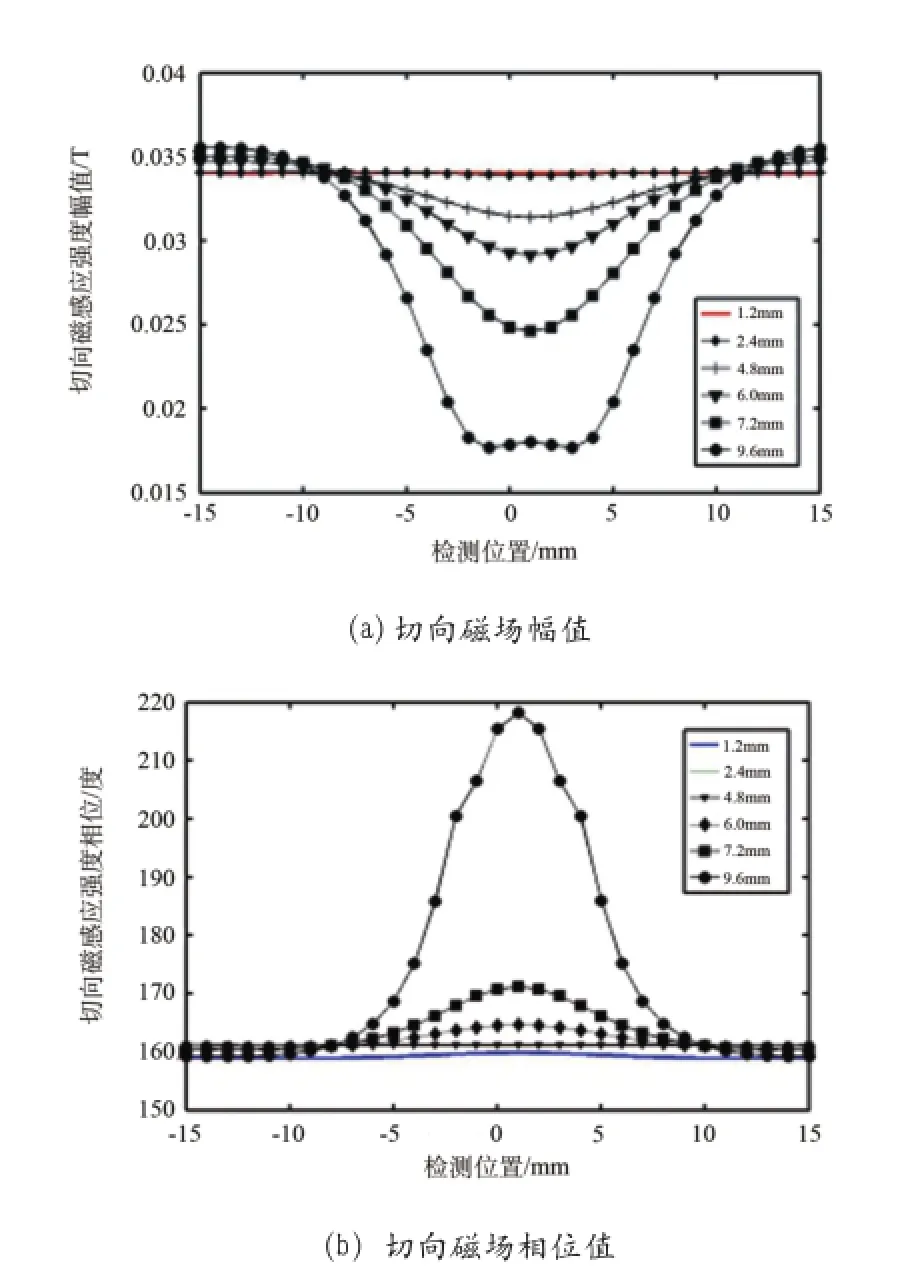
图8 下表面切向磁场分量随缺陷深度变化分布


图9 下表面缺陷切向磁场分量随缺陷深度变化趋势
图10为缺陷位于下表面时,法向磁感应强度的幅值与相位随缺陷深度变化图。法向磁感应强的幅值信号形状与缺陷位于上表面时相似,呈N字型分布且随着缺陷深度的增加,信号的幅值逐渐增加,趋势如图11所示。由图10(b)看出,在1.2mm与2.4mm深度缺陷处,法向磁感应强度相位比较杂乱,检测结果没有规律性。随着缺陷深度的增加,信号逐渐趋于平稳,在缺陷处呈现单峰形状,但是计算结果的趋势没有明显的规律性,不足以用来描述缺陷深度变化。

图10 下表面法向磁场分量随缺陷深度变化分布
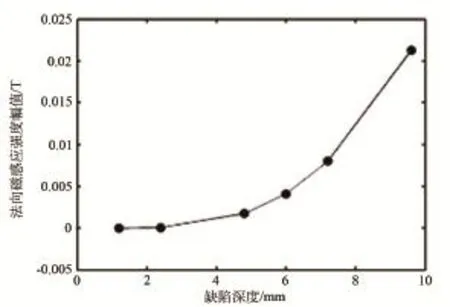
图11 法向磁场幅值随缺陷深度变化趋势
3 试验验证
为了验证仿真结果,笔者制作了三种不同材料,带有包括平底孔、台阶孔,裂纹缺陷在内的人工缺陷的试板共24块。在此选取的试验对象为厚度12mm的20#钢钢板,带有直径为5mm,深度为1.2mm,2.4mm,4.8mm,6mm,7.2mm以及9.6mm的人工缺陷。采用美国TesTex公司研制的PS2000检测仪及配套平板传感器进行试验。试验时,激励频率选取为10Hz,传感器提离选取为1mm,8通道进行扫查。试验系统如图13所示:

图12 某块试板
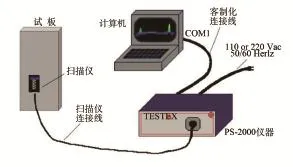
图13 试验平台示意图
图14为试验结果的截图,其软件界面由C扫与8通道波形图以及三维可旋转图组成,有利于直观地显示缺陷的信息。传感器经过缺陷处,在软件界面上会出现凸起的峰值,检测到缺陷处的最大相位与幅值的数值显示在软件界面上。笔者将缺陷的检测结果进行整理,见表2,磁场强度与相位均为相对值,直接摘自检测软件。
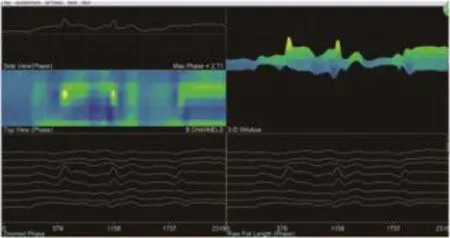
图14 试验软件界面图

表2 上下表面缺陷磁场强度与相位试验结果
试验数据表明,随着缺陷深度的增加,检测幅值峰值与相位均增大,与仿真结果趋势相符。对于下表面缺陷,当深度为1.2mm与2.4mm时,幅值较弱,在一般工程应用中,极有可能淹没在噪声中,达不到检测效果。
以缺陷深度为横坐标,检测得到的幅值与相位信息作为纵坐标,做出如下的趋势图15。可以清楚看出,上表面缺陷的检测值比下表面缺陷的更强。随缺陷深度的变化,相位值的趋势图近似成线性变化,而幅值图的线性规律并不强。因此,可以认为,试验中,相位值能够更加清晰地表征上下表面缺陷深度的变化。


图15 试验结果趋势图
4 结论
针对低频交流励磁检测技术在碳钢材料外表面腐蚀缺陷检测问题,本文进行了基于低频交流励磁检测技术的仿真研究,得出如下结论:
1)低频交流励磁检测技术可以用于快速发现钢板上下表面的缺陷且对于较厚钢板的检测较灵敏度较高;
2)仿真结果表明,缺陷信号的切向磁感应强度信息能够更好地表征缺陷的深度信息,其检测值随着缺陷深度的变化近似呈线性分布;
3)随着缺陷深度的变化,试验结果与仿真结果的趋势大致相符,且试验结果表明信号的相位信息较幅值信息能够更好地表征缺陷深度的变化。
参考文献
[1] Theodoulidis T, Kriezis E.Series expansions in eddy current nondestructive evaluation models[J].Journal of materials processing technology, 2005, 161(1): 343-347.
[2] Zhang D L, Cao Y N, Wang C, et al.A new method of defects identification for wire rope based on three-dimensional magnetic flux leakage[C].Journal of Physics: Conference Series. IOP Publishing, 2006, 48(1):334-338.
[3] 吴德会,游德海,柳振凉,等.交流漏磁检测法趋肤深度的机理与实验研究[J].仪器仪表学报,2014, 35(2): 327-336.
[4] 任吉林,林俊明,高春法.电磁检测[M].北京:机械工业出版社,2000:91-93.
[5] 倪光正,钱秀英.电磁场数值计算[M].北京:高等教育出版社,1996:79-80.
Influence of Defect Depth on Result of Low Frequency Electromagnetic Testing
Lu Xinyuan1Li Guanghai2Yang Jianfeng1
(1. Beijing University of Chemical Technology Beijing 100029)
(2. China Special Equipment Inspection and Research Institute Beijing 100029)
AbstractWith the low frequency electromagnetic technology simulation research and experiment result, external and internal corrosion defects in the pressure equipment were studied. Based on the low frequency electromagnetic simulation model, the paper mainly discussed the inspection results influenced by the defect depth. The amplitude and phase of magnetic field changing with the depth of defects were carried out and the experiments were conducted. According to the results, the experiment result was accordance with the simulation.
KeywordsLow frequency electromagnetic Non-destructive testing Finite element simulation Least square fitting
作者简介:陆新元(1990~),女,硕士,从事电磁无损检测技术的研究工作。
收稿日期:(2016-02-29)
中图分类号:X922
文献标识码:B
文章编号:1673-257X(2016)06-0044-06
DOI:10.3969/j.issn.1673-257X.2016.06.011

