基于粒子群优化匹配追踪的风机振动信号去噪处理
甘晓晔 李丽娜 曾庆勋 张兆刚
1(辽宁科技学院机械工程学院 辽宁 本溪 117000)2(辽宁大学物理学院 辽宁 沈阳 110036)
基于粒子群优化匹配追踪的风机振动信号去噪处理
甘晓晔1李丽娜2*曾庆勋2张兆刚1
1(辽宁科技学院机械工程学院辽宁 本溪 117000)2(辽宁大学物理学院辽宁 沈阳 110036)
摘要针对风力机振动信号采集过程中易受噪声影响的问题,提出基于过完备原子库的匹配追踪算法对风机振动信号进行处理。该算法能自适应提取和原子相关的信号结构,从而可实现噪声抑制。在匹配追踪算法处理过程中,利用结合梯度信息的改进的粒子群优化算法来寻找最佳原子。仿真结果表明,该算法比标准匹配追踪算法具有更快的运算效率及更高的重构精度。利用该算法对风力发电机齿轮箱振动信号进行去噪处理实验。实验结果表明,去噪后信号信噪比可提高5 dB以上,波形特征更加清晰,并且可以在降噪的同时有效保留故障信息。
关键词匹配追踪粒子群优化梯度信息风机振动信号去噪处理
0引言
风力发电机振动信号是对风机运行状况进行监测及故障分析与诊断的重要依据。风力发电机通常工作于偏远地区,工作环境恶劣,非常容易受到风力等因素的影响。加之布线复杂且长度较长,也易受到电磁及工频干扰,使得振动信号中不可避免的混入随机噪声信号,源信号的信噪比较低,信号特征模糊,影响后续的振动信号分离与故障诊断的准确性。因此寻找一种有效的去噪方法势在必行。
匹配追踪MP(MatchingPursui)算法是90 年代初由Mallat和Zhang等提出的一种优秀的稀疏分解重构算法[1]。该算法是将信号表示成与信号结构匹配原子的线性展开,能够利用较少的原子准确地描述信号特性,因此可在保留信号最主要结构特征的前提下有效地降低信号处理的成本[2-4]。由于MP算法中,稀疏分解重构的是信号与原子结构特性相匹配的部分,而噪声信号通常都是随机的、不相关的、非预期的、没有结构特性。因此该算法可以很好地抑制噪声,实现降噪消噪的目的[5-7]。
MP算法是一种贪婪算法,与其他稀疏分解算法相比有着相对高效的处理速度和准确的重构精度,是目前信号稀疏分解最常的用方法。但因MP稀疏分解算法是基于过完备的原子库的,每次迭代都要从过完备原子库中寻找最佳匹配原子,因此导致其计算量非常大,使得在特定类型的信号的稀疏分解上存在处理速度不够快,处理实时性无法满足要求等一系列问题。对此,也有少数学者做了一些改进尝试,但大多集中在对原有遗传算法的改进方面[8-10],虽然在一定程度上提高了MP分解速度和精度,但却带来了复杂的编码和解码方式以及交叉和变异等操作,搜索效率较低。另外,因遗传算法本身仍属于局部寻优算法,只能求得近似解,尤其在使用MP分解提取信号微弱特征时将受到很大限制。
鉴于此,本文将可全局寻优、算法简单、计算快速、易编程实现的粒子群优化算法PSO引入到MP稀疏分解过程中,并结合梯度信息对PSO算法本身进行了改进。利用此改进的PSO算法来寻找最佳匹配原子,可使寻找到的原子更具有结构特性,将在一定程度上提高算法的匹配精度,将其用于风机振动信号处理,将获得更好的降噪去噪效果。同时,可有效地减少MP算法计算量、缩短计算时间。
1基于改进PSO优化的MP算法实现
1.1MP稀疏分解算法原理
MP算法是传统稀疏分解算法中最广泛使用的一种。一个任意信号X,都可以表示为:
(1)
其中RkX为原信号X在第k次迭代之后的残差信号,gmk是定义在参数组m上,第k次迭代在过完备原子库中被选中的原子。而gmk必须满足与RkX内积绝对值最小,如下:
(2)
其中Γ为参数组m的集合。
1.2基于梯度信息改进PSO优化MP算法
由式(2)可知,MP稀疏分解算法中每次迭代都要计算残差与每个原子投影,再取绝对值最大的原子。由于信号在高维空间中,而且原子库是过完备的,所以进行这种内积计算的计算量大、效率低。针对这个致命缺陷,可以结合粒子群优化算法,将适应度函数选为信号或残差信号与原子的内积的绝对值,便可有效地提高算法计算效率。
粒子群算法是一种模仿动物群体运动的群体智能算法之一[11]。在d(d=1,2,…,D)维空间中有m个粒子,每个粒子均在寻找适应度函数可能解。其中,第i个粒子的解为xid,其经历的自身最优解为pid,整个种群的全局最优解为pgd,更新的速度为vid,则第i个粒子的更新速度为式(3),解值为式(4):
(3)
(4)
其中t为迭代次数,c1、c2为加速常数,代表了自身最优解与全局最优解的权重。rand1与rand2为[0,1]上的随机数。如果建立一个合适的适应度函数表示某一原子与原信号匹配程度,并且利用经典PSO算法对适应度函数的求解过程进行优化,则可以提升MP算法的速度。匹配追踪是通过把原函数投影到字典的元素上,此过程中,最佳匹配与原信号的内积最大。结合PSO算法的特性,适应度函数可以选为原信号与字典元素的内积的绝对值来进行优化迭代,可以快速寻找到最匹配原子。
在实际应用中,PSO算法是一种全局优化算法,局部搜索能力比较弱,导致后期收敛速度变慢。其次,若算法参数设置欠妥,则很容易陷入局部极值[12-16]。鉴于这两个缺点,可以结合梯度信息对PSO算法加以改进[17,18]。即先用PSO使适应度函数的解值快速定位在极值的附近,再用梯度算法迅速找到极值。
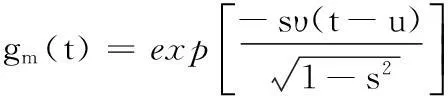
(5)
由于信号是离散的,所以用求和代替积分,则一阶梯度为对四个参数依次求偏导:
u)+φ]RkX(ti)}
(6)
(7)
(8)
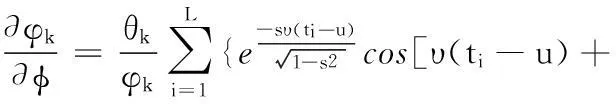
(9)
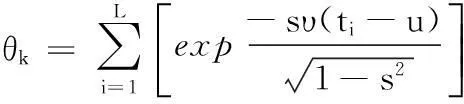
1.3仿真实验与分析
为了验证本文基于改进PSO优化的MP算法的可行性及检验算法改进后的性能,在普通PC机上对一维信号进行了稀疏分解与重构仿真实验研究,对算法的运算效率和重构精度两方面进行了评估。仿真实验用PC机采用Inteli3 双核CPU,主频分别为3.40和3.39GHz,内存容量1.86GB,安装WindowsXPSP3操作系统。
如图2(a)所示,随机产生一个一维的原始仿真信号,利用传统MP算法对其进行稀疏分解,得到稀疏系数如图2(b)所示。
由图2(b)可得,其稀疏系数呈现明显快速衰减,其中非零的个数远小于总长度,故体现出稀疏表示的稀疏性。再利用这些非零稀疏系数,对原始信号重构,得到的信号如图2(d)所示。由图2(c)可以看出,虽然相较于原信号存在一定程度的信号冗余,但是其失真率仍在实验精度要求范围之内,且重构信号的维数远小于原信号。整个算法用时为55.94682秒。
作为对比,输入信号与图1相同,利用本文所提出的改进PSO算法对MP进行优化,对图2(a)所示的原始仿真信号进行稀疏分解与重构,迭代次数为16,原子个数为3,结果如图3所示。对比图2,可以看出稀疏衰减更快,信号冗余更小,重构信号的精度更高。最重要的是整个算法的用时为11.609987秒,相较于传统算法来说有了大幅减少。以上仿真实验表明,利用本文基于改进PSO优化的MP算法较基本MP算法可明显提高运算效率和重构精度。
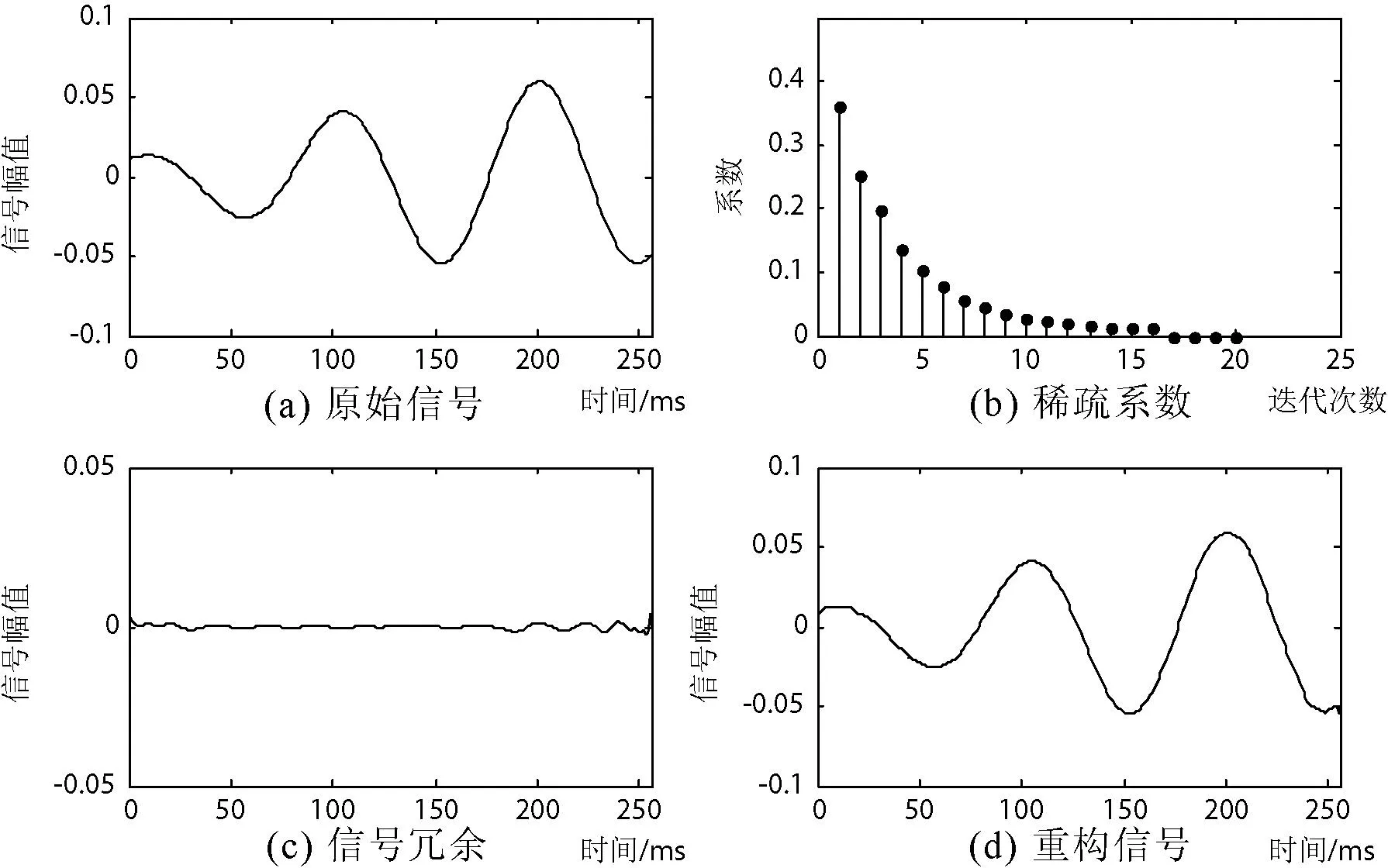
图2 传统MP算法信号稀疏分解重构结果
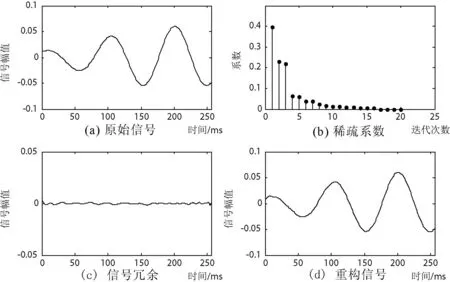
图3 改进PSO优化MP算法信号稀疏分解重构结果
2基于改进MP算法的信号去噪分析
由于MP算法能自适应的提取和原子相关的信号结构,因此可以很好地抑制噪声,实现降噪消噪的目的。
目前公认的去噪效果较好的方法是基于小波变换的小波去噪,连续小波变换常定义为:
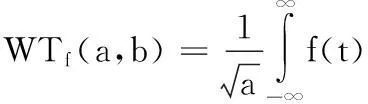
(10)
因噪声是常见而且不可避免的,常用线性瞬时混合模型对含有噪声的原信号进行建模。可以表述为:
Xm=Asm+Nm
(11)
其中Xm为m维含噪观测信号,sm为原信号,Nm为噪声。假设原信号各分量为相互统计独立,若Nm不是高斯噪声,则观测信号Xm是对于原信号sm的有偏估计。显然在对混合信号做盲分离等处理时,若要提高算法精确度,去噪处理势在必行。
如前文所述,匹配追踪每次迭代之后都会留下残差。一般来说,迭代次数越多,残差越小,算法精度也就越高。但是在去噪处理中,经过多次迭代,残差信号的信噪比比较低,噪声的匹配系数会很大,会被当成有用信号被保留,这样对于去噪处理是不利的。实验中如果放弃衡量残差的大小而选用较为合适的迭代次数为算法停止条件,这样在损失部分信号能量的情况下能使噪声得到很好的抑制。
3风机齿轮箱振动信号去噪实验研究
3.1去噪实验
为进一步验证算法的可行性及实用性,利用本文算法还进行了风机齿轮箱振动信号的去噪处理实验。信号采集自内蒙古自治区赛汉塔拉龙源风场的风机齿轮箱,该风场风机投入运行两年,运行时发现某风机齿轮箱高速端振动剧烈,并伴有较大的噪音。实验时,在该齿轮箱高速端及低速端风别布置两个传感器,采集到的振动信号如图4所示。
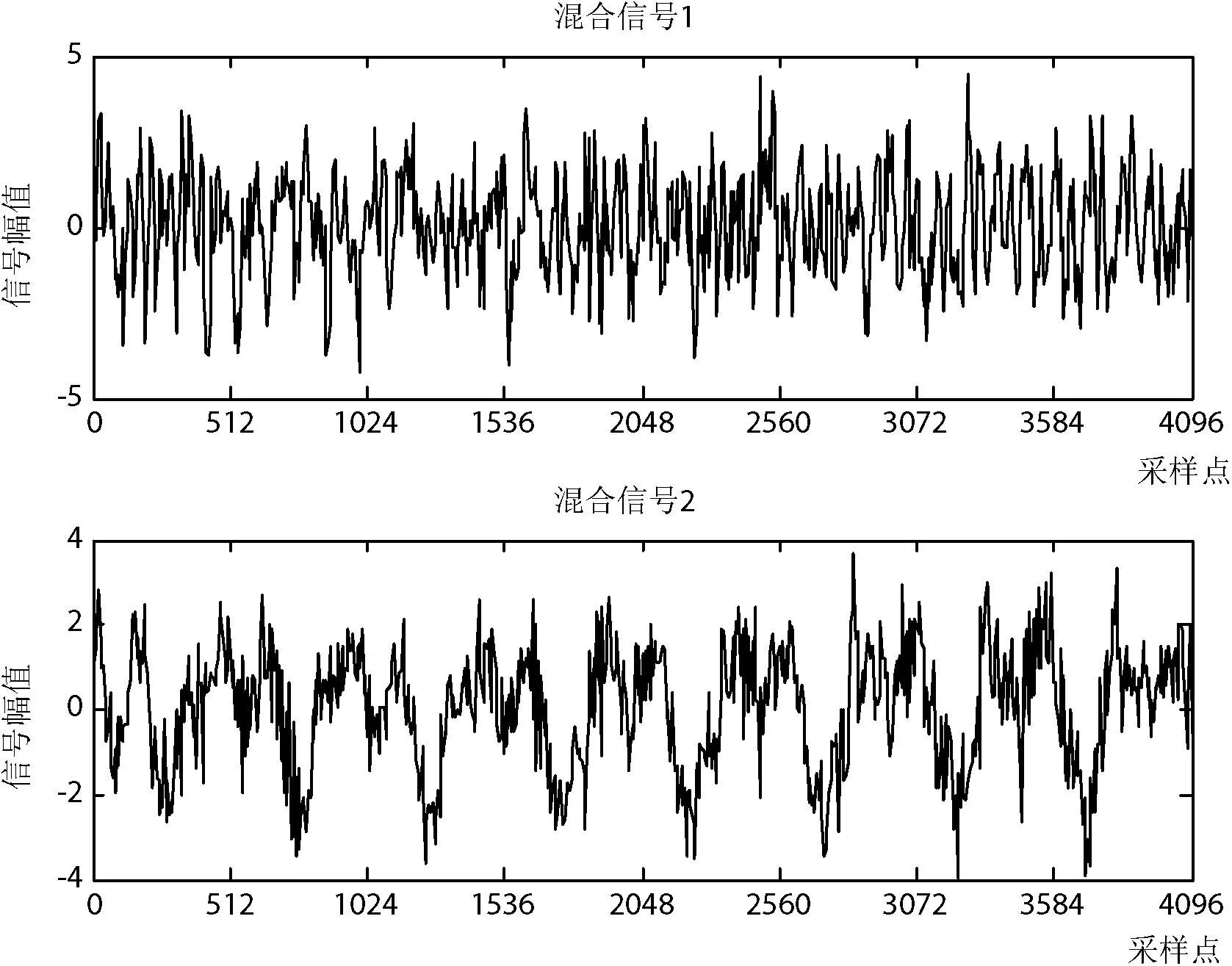
图4 故障风机齿轮箱振动信号
针对风机齿轮箱振动信号特点,采用离散余弦基建立原子库,利用本文改进PSO优化MP算法对图4所示振动信号进行去噪处理。采用固定迭代次数,得到去噪后风机齿轮箱混合信号如图5所示。与图4相比,应用本文算法进行MP去噪后的风机混合信号显然平滑、清晰许多,信号的特征规律更加明显。
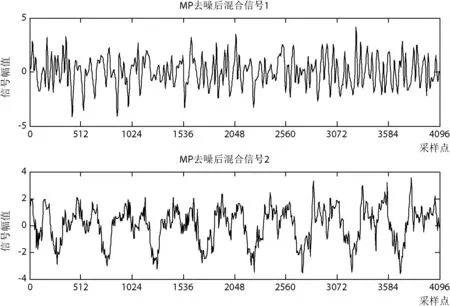
图5 PSO优化MP去噪后故障风机齿轮箱振动信号
为检验去噪后故障信息是否得以保留,又以相同方式布置测点,采集同一风场已确定为运行正常的某风机的齿轮箱振动信号。同样应用本文改进PSO优化MP算法进行去噪处理,得到去噪后的振动信号如图6所示。

图6 PSO优化MP去噪后正常运行风机齿轮箱振动信号
对去噪后的故障风机及正常运行风机齿轮箱振动信号利用文献[19]方法分别进行欠定盲源分离后各得到4路信号,对比分离结果,初步判断故障点在风机齿轮箱高速端。限于篇幅,在此只给出分离出的高速端振动信号分别如图7及图8所示,对其进行功率谱分析,结果分别如图9及图10所示。根据风力机齿轮箱各级齿轮的齿数及正常工作状态下的转速可以计算各级齿轮的啮合主频率如下:输入级即低速端53.71Hz,中间级197.23Hz,输出级即高速381.62Hz,对比功率谱分析结果可以看出,在故障风机齿轮啮合频率峰值约380Hz处的左侧边频带显著加强,而在800Hz左右的高频段出现了异常频率成分。参阅齿轮箱故障诊断文献可知,此为齿轮疲劳点蚀所表现的典型故障特征。随后对该风机齿轮箱进行拆机检修,确认中低速端各零部件工作正常,高速端齿轮副疲劳,因此,经本文算法去噪后,很好地保留了故障信息。

图7 故障风机齿轮箱高速端振动信号

图8 正常运行风机齿轮箱高速端振动信号

图9 故障风机齿轮箱高速端振动信号功率谱分析

图10 正常风机齿轮箱高速端振动信号的功率谱分析
3.2去噪实验结果分析
风机齿轮箱为旋转机械结构,参考齿轮箱相关的故障原因及资料可知,其中齿轮故障、轴承故障与轴故障所占比例接近总故障率的90%,而其故障特征均具备周期性,即具有结构特征。因此,用本文MP算法对风机齿轮箱振动信号进行去噪处理,由于稀疏分解重构的是信号与原子结构特性相匹配的部分,所以具备周期性的、具有结构特征的信号信息,包括正常的风机振动信号与有用的故障信息,都将得以保留;而例如白噪声、风力等原因产生的随机噪声将被去除,从而可有效提高信号信噪比。对去噪效果进行定量分析可知,两路振动信号去噪前后其信噪比分别提升5.7430dB和6.0411dB。
4结语
本文提出了利用改进PSO算法在匹配追踪过程中寻找最佳原子的方法,不仅使算法的计算复杂度下降,计算效率提高,并且也在一定程度上提高了算法的匹配精度,将算法用于信号去噪,可获得更高的信噪比。
对风机齿轮箱振动信号的去噪实验结果表明,本文算法可在有效去噪的同时,很好地保留故障信息。除此之外,因风机齿轮箱振动信号不是真正的稀疏信号,而利用MP在去噪的同时,实现了信号的稀疏表示,这也是基于信号稀疏特性的欠定盲源分离算法所需要的[20,21],并且去噪后信号信噪比提高,更有助于提高后续欠定盲源分离算法的重构概率。
参考文献
[1]MallatS,ZhangZ.Matchingpursuitwithtime·frequencydictionaries[J].IEEETrans.OnSignalProcessing,1993,41(12):3397-3415.
[2]NeedellD,VershyninR.Uniformuncertaintyprincipleandsignalrecoveryviaregularizedorthogonalmatchingpursuit[J].FoundationsofComputationalMathematics,2009,9(3):317-334.
[3]RathG,GuillemotC.Sparseapproximationwithanorthogonalcomplementarymatchingpursuitalgorithm[C]//ProceedingoftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP),Taibei,Taiwan,2009:3325-3328.
[4]LiuYX,ZhaoRZ,HuSH.Regularizedadaptivematchingpursuitalgorithmforsignalreconstructionbasedoncompressivesensing[J].JournalofElectronics&InformationTechnology,2010,32(11):2713-2717.
[5]GillPR,WangA,MolnarA.Thein-crowdalgorithmforfastbasispursuitde-noising[J].IEEETransactionsonSignalProcessing,2011,59(10):4595-4605.
[6]LiS,FangL.Signalde-noisingwithrandomrefinedorthogonalmatchingpursuit[J].IEEETransactionsonInstrumentationandMeasurement,2012,61(1):26-34.
[7] 杜秀丽,沈毅.匹配追踪方法在超声检测信号去噪中的应用[J].无损检测,2006,28(8):406-412.
[8] 高瑞,徐华楠,胡钢.基于GA和过完备原子库划分的MP信号稀疏分解算法[J].科学技术与工程,2008,8(4):914-916.
[9] 李恒建,尹忠科,王建英.基于量子遗传优化算法的图像稀疏分解[J].西南交通大学学报,2007,42(1):19-23.
[10] 李明,李应.基于遗传算法优化匹配追踪的自然环境声音分类[J].福州大学学报:自然科学版,2012,40(6):719-725.
[11]KennedyJ,EberhartRC.Particleswarmoptimization[C]//Proc.IEEEInternationalConferenceonNeuralNetworks,PiscatawayNJ:IEEEServiceCenter,1995:1942-1948.
[12] 熊南,刘百芬.基于自适应粒子群优化LSSVM的网络流量在线预测[J].计算机应用与软件,2013,30(9):21-24,127.
[13] 安晶,徐森.一种结合粒子群优化理论改进的郭涛算法及其应用[J].计算机应用与软件,2014,31(2):296-299,320.
[14] 陈志敏,薄煜明,吴盘龙,等.收敛粒子群全区域自适应粒子滤波算法及其应用[J].南京理工大学学报,2012,36(5):861-868.
[15]ZhangLP,YuHJ,HuSX.Optimalchoiceofparametersforparticleswarmoptimization[J].JournalofZhejiangUniversity:NaturalScience,2005,6(6):528-534.
[16]JansonS,MartinM.Ahierarchicalparticleswarmoptimizationfordynamicoptimizationproblems[C]//EvoWorkshops,2004,LNCS3005,2004:513-524.
[17] 王俊伟,汪定伟.一种带有梯度加速的粒子群算法[J].控制与决策,2004,19(11):1298-1300,1304.
[18] 肖健梅,李军军,王锡淮.梯度微粒群优化算法及其收敛性分析[J].控制与决策,2009,24(4):560-564.
[19] 李丽娜,曾庆勋,甘晓晔,等.基于势函数与压缩感知的欠定盲源分离[J].计算机应用,2014,34(3):658-662.
[20] 何继爱,何勇,肖丹丹.基于KM-PCA稀疏信号的盲源分离算法[J].兰州理工大学学报,2012,38(4):80-84.
[21] 董天宝,杨景曙.稀疏盲源分离快速算法[J].活力与指挥控制,2012,37(7):84-87.
WIND TURBINE VIBRATION SIGNAL DENOISING PROCESSING BASEDONMATCHINGPURSUITOPTIMISEDBYPSO
Gan Xiaoye1Li Li’na2*Zeng Qingxun2Zhang Zhaogang1
1(School of Mechanical Engineering,Liaoning Institute of Science and Technology,Benxi 117000,Liaoning,China)2(School of Physics,Liaoning University,Shenyang 110036,Liaoning,China)
AbstractAiming at the problem that in the process of wind turbine vibration signal collection it is easily to be affected by noise, we proposed an over-complete atom dictionary-based matching pursuit algorithm to process the wind turbine vibration signal. The algorithm can adaptively extract the signal structure correlated with the atom, so that the noise suppression can be achieved. And in the process of matching pursuit algorithm operation, it uses an improved particle swarm optimisation algorithm in combination with the gradient information to search optimal atoms. Simulation result showed that the proposed algorithm had higher computation efficiency and signal reconstruction accuracy than the basic matching pursuit algorithm. Moreover, based on this algorithm, we carried out the experiment of denoising processing on the vibration signal of wind turbine gearbox, experimental result showed that the signal-to-noise ratio of the denoised signal could be improved to 5 dB and higher, the waveform features were more clearly, and while denoising, the fault information could be effectively reserved as well.
KeywordsMatching pursuitParticle swarm optimisationGradient informationWind turbine vibration signalDe-nosing processing
收稿日期:2015-01-10。辽宁省自然科学基金项目(201102093);辽宁省教育厅科学技术研究项目(L2013489)。甘晓晔,教授,主研领域:信号处理及故障诊断技术。李丽娜,副教授。曾庆勋,硕士生。张兆刚,副教授。
中图分类号TP301.6
文献标识码A
DOI:10.3969/j.issn.1000-386x.2016.06.064

