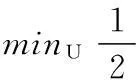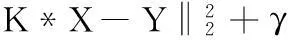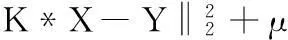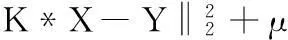基于双L0稀疏先验的图像运动去模糊

陶宗勤　方贤勇,2　谈业静　陈尚文

1(安徽大学媒体计算研究所　安徽 合肥 230601)2(南京大学计算机软件新技术国家重点实验室　江苏 南京 210023)



基于双L0稀疏先验的图像运动去模糊

陶宗勤1方贤勇1,2谈业静1陈尚文1

1(安徽大学媒体计算研究所安徽 合肥 230601)2(南京大学计算机软件新技术国家重点实验室江苏 南京 210023)

摘要目前图像的运动去模糊方法在处理较复杂的运动模糊时难以得到理想的效果，其原因之一是这些方法普遍只考虑图像梯度的稀疏性，忽略了模糊核的稀疏性。针对这一不足提出一种新的双L0正则约束的运动模糊去除方法，该方法同时对自然图像梯度和模糊核使用L0正则约束，结合半正定二次分裂最小化的方法进行求解优化，实现自然模糊图像梯度和模糊核均稀疏下的模糊核估计，并进一步使用L0.5超拉普拉斯正则约束项恢复最终图像。实验发现，该方法可以较好地去除单幅图像较复杂的运动模糊，更好地克服了估计的模糊核中存在的噪点和错误，得到较现有方法更加理想去模糊效果。

关键词L0正则约束运动去模糊半正定二次分裂

0引言

随着数码相机和移动设备的普及，数字图像已在生活和工作中广泛应用。但是，由于相机或物体间的相对运动等原因，运动模糊的图像经常见到。如何去除运动模糊，得到清晰的图像是件非常有意义，但又较难解决的问题。本文针对这一问题进行研究，提出一个新的基于图像梯度和模糊核的双L0稀疏正则约束的运动去模糊方法。

由于产生模糊的运动过程以及原始的清晰图像均未知，这一病态的去模糊研究也被称为盲运动去模糊[1-3]。为了实现清晰图像的还原，这一研究普遍采用图像先验知识进行约束求解。早期的方法通常采用高斯平滑去惩罚自然图像或图像梯度，但这种先验知识无法保留图像的清晰边缘。为了克服这个问题，许多正则化的方法被提出[4,5]。由于自然图像梯度很难服从高斯分布[6]，Fergus等[1]提出一种混合高斯方法适应自然图像的梯度信息，以及一个混合指数先验模拟模糊核。Shan等[2]采用图像的稀疏先验知识，首先使用一个大的正则约束权值抑制图像中不重要的结构，并保存重要的结构，这样使得在迭代过程中模糊核朝着正确的方向进行。Amizic等[7]在图像梯度上利用一个超高斯的先验分布[8]，以及在模糊核上使用全变分的先验约束。Krishnan等[9]在图像上使用一个L1/L2的正则约束项，主要是在迭代过程中使用L1正则约束项的基础上将图像梯度的L2范数当作一个权值。这些工作都是基于自然图像统计得到的重尾分布[1]或其变体方法，利用了其在恢复图像的过程中能够很好地保持图像重要细节的特性。

但是这些基于自然图像统计的方法虽然能够很好地保持图像的细节，却在处理复杂模糊核时并不能得到比较理想的结果。文献[10-12]中提出在估计运动模糊核的过程中，一般的自然图像统计方法(Lp正则约束方法(0

虽然运用L0范数约束图像稀疏性能够得到比较理想的恢复结果，但是其得到的模糊核却存在一些瑕疵。具体表现为：现有对图像梯度实施L0正则约束的方法求出的模糊核虽然可以得到一个较为准确的运动路径。但在处理一些较为复杂的运动模糊时，得到的路径周围存在较多的噪点和错误，由于这些错误信息的干扰，难以取得理想的去模糊效果。我们认为，产生这一现象的原因之一是这些方法没有考虑产生运动模糊的运动路径在空间上是稀疏的，即没有考虑运动模糊核本身的稀疏性，从而无法得到准确的模糊核。为此，本文考虑模糊核的稀疏性，并进一步将其与Pan等提出自然图像的稀疏性相结合，提出双L0约束下模糊核求解方法。该方法使用L0约束项同时约束模糊核和图像梯度的稀疏性，实现运动模糊核的估计。

由于L0正则约束是一个难以直接计算的问题，我们将Xu等[16]提出的半二次分裂最小化方法引入到本文方法的求解过程中。该方法根据图像的L0约束可以在全局上控制图像中非零梯度值的数量，从而并不再依赖图像的局部特征，得到较为理想的去模糊效果。本文方法可以简述为：运用迭代的方法求取模糊核，在迭代的过程中，对中间图像梯度和模糊核同时使用L0的正则约束项；分别使用半二次分裂最小化方法实现模糊核和清晰图像的双L0正则约束下的求解，即通过引入一个辅助变量将原有问题分裂成两个有闭合解的子问题，从而得到一个最佳的逼近解。在最终图像的恢复阶段使用的是Krishnan[8]提出的超拉普拉斯分布逼近自然图像的重尾分布。

1双L0正则约束估计模糊核

1.1通常的图像去模糊模型

图像模糊的数学模型可以表示为：

B=K*U+N

(1)

其中B表示观测到的模糊图像，K表示模糊核，U表示对应的清晰图像，N表示噪声，*表示卷积符号。

从模糊图像B恢复到清晰图像U的过程是一个成像的逆过程，然而由于噪声的存在，这种恢复过程通常是病态的，这样一般的逆滤波方法[17]并不能得到一个理想的结果。为了获得更好的结果，通常采用正则化方法建模得到能量最小化方程，然后进行求解：

(2)

其中第一项是数据保真项，用来控制解的逼近程度；第二和三项为正则项，用来约束信号的能量；λ为图像正则项参数，用来调节图像先验知识的权值；γ是模糊核正则项参数，用来调整模糊核先验知识的权值。φ(U)和ω(K)分别代表图像和模糊核的先验知识的正则项，根据正则项的不同，可以产生不同的正则化方法。目前提出的正则化方法主要有表 1所示的几种。可以看出：在图像的约束项方面，非自然图像统计的L0正则约束项具有更好的恢复结果，而在模糊核的先验约束上，很少有人考虑L0的稀疏约束。

表1　现有正则化方法的正则约束项

1.2双L0估计模糊核模型

模糊核的估计对去运动模糊是至关重要的，通过对比发现，文献[9,10,19]等利用自然图像统计得到的Lp(0

这一双L0约束的模型可表示为下面的能量最小化表达式：

(3)

基于上述表达式的模糊核和清晰图像求解可直接使用MAP框架[9, 13, 14, 18]，即将上面的模型分成两步反复迭代求解。首先初始化一个模糊核，利用这个模糊核求清晰图像梯度，然后利用这个图像梯度估计模糊核，之后再利用估计得到的模糊核继续求清晰图像。图1给出双L0估计模糊核算法的流程图。

图1　双L0求取模糊核流程图

1.3L0估计中间图像

由式(3)可以得到求解中间图像的模型为：

(4)

由于式(4)是一个离散优化问题，这类问题利用传统的梯度下降法以及一些离散优化方法非常难以解决。这里利用交替逼近的半正定二次分裂L0最小化方法。首先引入一个辅助变量G，这个G对应于图像U的梯度信息X，然后将式(4)重写成下面的形式：

(5)

其中μ趋近于无限大时，这样可以使式(5)的解接近于式(4)。而模型式(5)可以通过一个交替最小化G和X的方法解决。

可将G初始化为一个全0的矩阵，这样每一步迭代过程中，可以用以下的模型求X：

(6)

这是一个最小二乘最小化问题，它的闭合解为：

(7)

然后，可由得到的X求出G：

(8)

这是一个针对每个像素求式(8)最小值的问题，根据文献[16]的证明可以得到相应的解为：

(9)

1.4L0估计模糊核

类似于式(3)，模糊核可以通过如下的模型求解：

(10)

式(10)的解法与求解中间图像梯度类似。首先引入一个辅助变量H，这个H对应于模糊核K，然后将式(10)重写成下面的形式：

(11)

其中β趋近于无限大，这样可以使式(11)的解接近于式(10)。而对模型式(11)可以通过一个交替最小化H和K的方法解决。

同样，可将H初始化为一个全0的矩阵，这样每一步迭代过程中，可以用以下的模型求K：

(12)

式(12)的闭合解为：

(13)

进一步，由得到的K可求H：

(14)

得出相应的解为：

(15)

1.5最终清晰图像的恢复

上面得到的X是清晰图像的梯度，并不是最终的恢复图像，还缺少了图像的细节部分。因此在最后一步，可利用上面得到的模糊核K，然后用一个非盲的去卷积算法得到最终的恢复图像。这里使用的是文献[8]给出的超拉普拉斯方法，使用的是L0.5的正则约束项，模型如下：

minuλ1‖K*U-B‖2+‖U‖0.5

(16)

1.6核心代码

本文使用MAP框架，利用半正定二次分裂最小化方法得到最优逼近解，这里给出求解中间图像的核心代码，求解模糊核的代码和求解中间图像类似：

function[Sx,Sy] =L0deblur_smooth(Sx,Sy,kernel,lambda,opts)

betamax= 1e2;

[N,M,D] =size(Sx);

sizeI2D= [N,M];

KER=psf2otf(kernel,sizeI2D);

Den_KER=abs(KER).^2;

Normin1_x=fft2(Sx);

Normin1_y=fft2(Sy);

ifD>1

% 维度大于1时，扩充维度

Den_KER=repmat(Den_KER,[1,1,D]);

end

beta=opts.mu;

kappa=opts.rho;

whilebeta

Denormin=beta+Den_KER;

% 求出公式(7)中的分母

h=Sx;

% 清晰图像梯度(x轴方向)

v=Sy;

ifD==1

ht=h.^2

% 得到小于阈值的像素点矩阵

vt=v.^2

else

ht=sum((h.^2),3)

ht=repmat(ht,[1,1,D]);

vt=sum((v.^2),3)

vt=repmat(vt,[1,1,D]);

end

h(ht)=0;v(vt)=0;

FSx=(conj(KER).*Normin1_x+beta*fft2(h))./Denormin;

FSy=(conj(KER).*Normin1_y+beta*fft2(v))./Denormin;

Sx=real(ifft2(FSx));

% 逆傅里叶变换求取结果

Sy=real(ifft2(FSy));

beta=beta*kappa;

end

end

2实验

为了验证上述方法的可行性和效果，本文分别对人造图像和真实图像进行了大量的实验。本实验的实验环境为：Window7 64位操作系统，8GB内存，CPU为Inter奔腾G620，软件为Matlab2013a。实验主要针对文献[9,13,14]进行对比，这些文献中提出的方法都是最近效果比较好，并且比较有代表性的正则化方法。实验中对仿真图像分辨率为600×800，噪声是参数为0.001的随机噪声。并且分辨率越大运行时间越长，噪声越大得到的恢复效果越差。每幅效果图右边从上到下的三幅小图分别为模糊核、上方和下方白色小块放大图，其中标题为“清晰图像”和“模糊图像”的子图中的模糊核为真实的模糊核，其他的为算法估计得到的模糊核。

图2是图像卷积模拟的模糊核后各算法的恢复结果。(a)是实际拍摄得到的清晰图像，分辨率为600×800；(b)是卷积一个59×59的模糊核后加噪声形成的模糊图像；(c)是文献[9]恢复结果，可以看出在模糊核比较大的时候，Krishnan等方法则会失效；(d)是文献[13]的恢复结果，从图中可看出虽然此方法可以求出一个接近的模糊核，但存在较大的错误；(e)是文献[14]的恢复结果，从图中可以看到模糊核的主干部分基本求的比较准确，但周围存在较多的噪声和错误；(f)是本文的恢复结果，可以看出本文方法求出的模糊核是比较理想的。这个实验说明在处理模拟运动模糊的情况下，本文方法更有优势。

图2　模拟运动模糊的恢复结果

本文方法对真实的模糊图像同样可以取得较好的去模糊结果。如图3所示是Krishnan等的方法中使用的真实模糊图像(分辨率为1024×1280，模糊核的大小为25×25)。其中，(a)为真实的模糊图像；(b)是文献[9]方法估计的模糊核和恢复结果，可以看出模糊核估计的并不准确；(c)是文献[13]估计的模糊核和恢复结果，从图可知模糊核还是有些偏差，导致恢复的效果不佳；(d)是文献[14]估计的模糊核和恢复结果，其得到的模糊核也不准确；(e)是本文方法得到的模糊核和恢复结果，从右边的局部放大图中可以看出，本文方法估计的模糊核和恢复结果都相对比较理想。

图3　真实运动模糊图像恢复结果

图4是利用最近效果比较好的几个算法对同一清晰图像卷积不同模糊核得到的模糊图像求取模糊核的结果(其中模糊核大小都为59×59)。从图中可以看出，L1/L2+L1方法在这种较大尺度复杂模糊核估计中完全失效，L0+L2的方法虽然可以得到模糊核的基本主干，但都存在很多噪点和错误信息从而影响去模糊效果；而本文的双L0方法估计的模糊核在大多数情况下能够很好的去除噪点和错误，从而得到更加理想的运动模糊核。

图4　估计的运动模糊图像的模糊核

图4中：第一行是真实模糊核；第二行是文献[9]方法估计的模糊核，利用L1/L2正则项约束项约束图像梯度，L1的正则项约束项约束运动模糊核；第三行是文献[13]方法估计的模糊核，利用L0的图像梯度约束项和L2的模糊核约束项；第四行是文献[14]方法估计的模糊核，利用L0的图像梯度约束项和L2的模糊核约束项；第五行是利用本文双L0方法估计的模糊核。

表2是利用文献[12]提供数据集中的8个模糊核来卷积拍摄到清晰图像并加上噪声，使用本文方法和最近效果比较理想的几个算法求解得到恢复结果的峰值信噪比对比。从表中可以看出本文方法是最接近于真实模糊核的恢复结果的。

表2　恢复结果的峰值信噪比对比

3结语

针对目前去除图像运动模糊的方法难以去除较复杂的模糊，以及当前L0方法存在的一些不足，提出双L0正则约束的运动模糊去除方法。该方法根据图像梯度的稀疏性以及运动模糊核的稀疏性，在估计模糊核的过程中对中间图像梯度和模糊核同时使用L0正则约束的稀疏先验，从而得到了一个更加鲁棒的运动去模糊模型；进一步，运用一个半正定二次分裂方法求解该模型，得到准确的模糊核；最后，使用L0.5的超拉普拉斯方法得到了较好的清晰原图像。实验结果表明该方法是可行的。以后的工作中将会考虑算法中参数的自适应调整问题和最终恢复图像中存在的振铃效应问题，以期得到更加清晰和准确的去模糊结果。

参考文献

[1]FergusR,SinghB,HertzmannA,etal.Removingcamerashakefromasinglephotograph[J].ACMTransactionsonGraphics(TOG).ACM,2006,25(3):787-794.

[2]ShanQ,JiaJ,AgarwalaA.High-qualitymotiondeblurringfromasingleimage[J].ACMTransactionsonGraphics(TOG).ACM,2008,27(3):73.

[3]ChoS,LeeS.Fastmotiondeblurring[J].ACMTransactionsonGraphics(TOG).ACM,2009,28(5):145.

[4]DaniilidisK,MaragosP,ParagiosN,etal.SingleImageDeblurringUsingMotionDensityFunctions[C]//DaniilidisK,MaragosP,ParagiosN.ComputerVision-ECCV2010.SpringerBerlinHeidelberg,2010:171-184.

[5]ChanTF,Chiu-KwongW.Totalvariationblinddeconvolution[J].ImageProcessing,IEEETransactionson,1998,7(3):370-375.

[6]FieldD.WhatIstheGoalofSensoryCoding?[J].NeuralComputation,1994,6(4):559-601.

[7]AmizicB,MolinaR,KatsaggelosAK.SparseBayesianblindimagedeconvolutionwithparameterestimation[J].EURASIPJournalonImageandVideoProcessing,2012,2012(1):1-15.

[8]KrishnanD,FergusR.Fastimagedeconvolutionusinghyper-Laplacianpriors[C]//AdvancesinNeuralInformationProcessingSystems,2009:1033-1041.

[9]KrishnanD,TayT,FergusR.Blinddeconvolutionusinganormalizedsparsitymeasure:ComputerVisionandPatternRecognition(CVPR)[C]//2011IEEEConferenceon,Providence,RI,2011:20-25.

[10]WipfD,ZhangH.RevisitingBayesianblinddeconvolution[J].EprintarXiv:2013(15):3595-3634.

[11]BenichouxA,VincentE,GribonvalR.Afundamentalpitfallinblinddeconvolutionwithsparseandshift-invariantpriors:Acoustics,SpeechandSignalProcessing(ICASSP)[C]//2013IEEEInternationalConferenceon,Vancouver,BC,2013:26-31.

[12]LevinA,WeissY,DurandF,etal.Understandingandevaluatingblinddeconvolutionalgorithms[C]//ComputerVisionandPatternRecognition,2009.CVPR2009.IEEEConferenceon.IEEE, 2009:1964-1971.

[13]JinshanP,ZhixunS.FastL0-RegularizedKernelEstimationforRobustMotionDeblurring[J].SignalProcessingLetters,IEEE,2013,20(9):841-844.

[14]LiX,ShichengZ,JiayaJ.UnnaturalL0SparseRepresentationforNaturalImageDeblurring:ComputerVisionandPatternRecognition(CVPR)[C]//2013IEEEConferenceon,Portland,OR,2013:23-28.

[15]PanJ,HuZ,SuZ,etal.DeblurringTextImagesviaL0-RegularizedIntensityandGradientPrior:ComputerVisionandPatternRecognition(CVPR)[C]//2014IEEEConferenceon,Columbus,OH,USA,2014:23-28.

[16]XuL,LuC,XuY,etal.ImagesmoothingviaL0gradientminimization[J].ACMTransactionsonGraphics(TOG),2011,30(6):174.

[17] 李沛秦,谢剑斌,陈章永,等.一种面向目标区域的快速去模糊算法[J].信号处理,2010(8):1240-1245.

[18]KoteraJ,roubekF,MilanfarP.Blinddeconvolutionusingalternatingmaximumaposterioriestimationwithheavy-tailedpriors[C]//ComputerAnalysisofImagesandPatterns.SpringerBerlinHeidelberg,2013:59-66.

[19]LevinA,WeissY,DurandF,etal.UnderstandingBlindDeconvolutionAlgorithms[J].PatternAnalysisandMachineIntelligence,IEEETransactionson,2011,33(12):2354-2367.

IMAGE MOTION DEBLURRING BASED ON DOUBLE L0SPARSE PRIORI

Tao Zongqin1Fang Xianyong1,2Tan Yejing1Chen Shangwen1

1(Institute of Media Computing,Anhui University,Hefei 230601,Anhui,China)2(State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210023,Jiangsu,China)

AbstractExisting image motion deblurring methods cannot obtain ideal results when dealing with the complex motion blurs. One of the reasons is that they generally only consider the sparsity of image gradients but ignore the sparsity of blur kernel. To overcome this limitation, this paper presents a new motion deblurring method with double L0 regular constraints, which applies the L0 regular constraints to both the natural image gradients and blur kernel, by combining the semi-definite quadratic splitting minimisation method it carries out the solution optimisation and realises the blur kernel estimation under the conditions of natural blurred image gradients and average sparsity of blur kernel. It further adopts a hyper-Laplacian term with L0.5regular constraint to restore the final deblurred image. Experiment finds that the proposed method can well remove the rather complex motion blur of single image and better overcome the estimated noise and errors in blur kernel, and consequently obtains a more ideal motion deblurring effect than existing methods.

KeywordsL0 regular constraintMotion deblurringSemi-definite quadratic splitting

收稿日期：2014-12-26。安徽省自然科学基金项目(1408085MF 113，1308085QF100)；南京大学计算机软件新技术国家重点实验室开放课题(KFKT2013B12)。陶宗勤，硕士生，主研领域：计算机视觉和计算摄影。方贤勇，教授。谈业静，硕士生。陈尚文，博士生。

中图分类号TP391.4

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.050