基于改进压缩感知的说话人识别抗噪算法

茅正冲　龚　熙

(江南大学轻工过程先进控制教育部重点实验室　江苏 无锡 214122)



基于改进压缩感知的说话人识别抗噪算法

茅正冲龚熙

(江南大学轻工过程先进控制教育部重点实验室江苏 无锡 214122)

摘要压缩感知CS(compressive sensing)是一种基于信号稀疏性，有效提取信号中有用信息的方法。根据语音信号和干扰噪声在离散余弦变换域DCT(discrete cosine transform)稀疏性的不同，提出一种基于改进压缩感知的说话人识别抗噪算法。在用正交匹配追踪OMP(orthogonal matching pursuit)算法重构语音信号时设定相关度阈值和语音恢复阈值，不仅有效恢复了语音信号，而且实现了语音增强。然后通过Gammatone滤波器组，对恢复语音信号进行处理，提取特征参数GFCC。仿真实验在高斯混合模型识别系统中进行，实验结果表明，将这种方法应用于说话人识别抗噪系统，系统的识别率及鲁棒性都有明显提高。

关键词压缩感知正交匹配追踪GFCC抗噪算法识别率

0引言

压缩感知(CS)作为近些年新兴的信号处理技术，是一种在采样过程中利用较少数据就能有效提取信号信息，然后通过重构算法从采样信息中恢复原信号的方法[1]。语音增强是指对带噪语音信号进行处理，降低噪声的干扰，恢复出较纯净的语音。所以，压缩感知与语音增强的本质是类似的。CS理论由于其边采样边压缩的特性使其具有了巨大的吸引力和应用前景，研究领域已经涉及到了雷达、无线传感、医学等领域。文献[2]将压缩感知理论运用到了随机调制雷达信号处理中，为随机调制雷达的低旁瓣信号处理提供了全新思路。文献[3]将合成聚焦于CS理论结合，解决了B超成像过程中数据量大的问题。

信号的稀疏性是压缩感知的前提和基础，但是正如语音和图像等信号，它们本身并不是稀疏的，但可以通过某种变换在其变换域中得到一个稀疏的信号以此来适用压缩感知。对于语音信号通常可以转换到DCT域、小波域等变换域来获得稀疏信号。文献[4]对语音信号在DCT域能显示出的近似稀疏性提出语音信号DCT域压缩感知。文献[5]利用语音信号自身构造了一种自相关观测矩阵，在同等重构性能下压缩率比其他随机矩阵更低。文献[6]在压缩感知的重构阶段设定相似度阈值来进行语音增强，该算法对非人声噪声有一定抗干扰作用。文献[7]提出了离散余弦小波包变换的语音信号压缩感知，构造出了更加稀疏的变换基，提高了重构的性能。

本文根据语音信号和干扰噪声在DCT域稀疏性的不同，在通过OMP算法重构带噪语音信号中的有用信息时，设置相关度阈值来限制迭代的次数，让尽可能少的噪声分量恢复出来。而当背景噪声类型于说话人信号时，仅设置相关度阈值不能有效恢复纯净语音信号，因为这时背景噪声和纯语音信号拥有相似的稀疏性。所以本文提出设置第二个门限阈值：语音恢复迭代阈值，以此来抑制人声背景噪声的回复。在重构过程中，如果低于此阈值，则迭代停止。这种双门限阈值的正交匹配追踪算法能够很好地应对不同的噪声环境场合，有效地实现语音增强。

1改进压缩感知说话人识别抗噪算法

1.1压缩感知基本原理

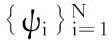
1.2DCT域稀疏性

对信号作压缩感知处理时，信号自身或者在变换域的稀疏性是对其进一步分析的重要前提。由于语音信号具有类余弦信号的周期特性，因此可以在DCT域来对其进行表示：

(1)

此时，Ψ为离散余弦基矩阵。经过DCT变换后的稀疏系数为Θ=(θ1,θ2,…,θN)T,θi=X(i-1),i=1,2,…,N，本文对一段语音“发布”截取一帧(512点)作DCT变换，并对DCT系数的绝对值进行降序排列，结果如图1所示。可以发现，在200～512之间的DCT系数都近似为0，说明信号在DCT域是稀疏的,可以采用压缩感知方法处理。

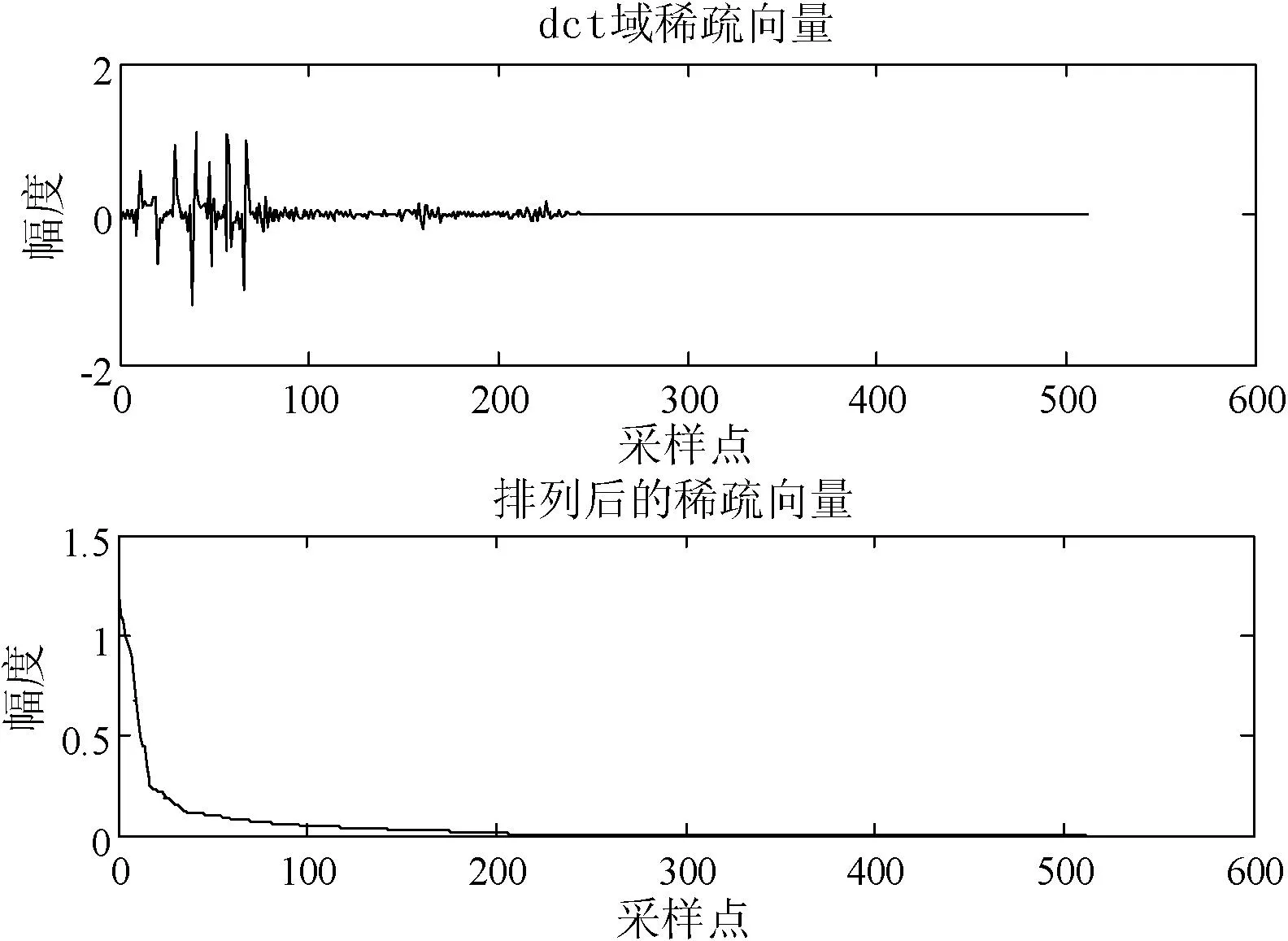
图1　DCT域系数分布及其降序排列

另外，本文对语音信号“发布”、高斯噪声以及babble噪声各取一帧作稀疏性对比，结果如图2所示。通过DCT系数绝对值的直方图发现，语音信号小幅度系数占了绝大部分，具有良好的稀疏性；高斯DCT系数比较均匀，舍弃小系数后作重构恢复，失真会很大，因而高斯噪声不具有稀疏性；babble噪声为一段嘈杂的人声背景噪音，观察图2(f)发现，babble噪声也具有较好的稀疏性。

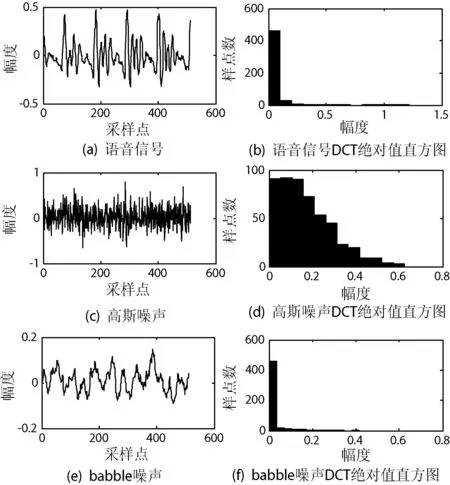
图2　语音信号和噪声在DCT域稀疏性对比

根据CS理论，对带噪语音信号进行低维投影，当观测矩阵维数足够包含语音信息时，投影后将丢失部分不具有稀疏性的噪声信息，重建时无法恢复。因此利用稀疏性不同的特性可以对语音信号进行去噪。然而，当采集的语音信号被类似于babble这样的人声噪声干扰时，仅根据稀疏性不同不能很好去噪，因为背景噪声同样具有较好的稀疏性。

1.3观测矩阵

观测矩阵Φ的选取对信号重构的性能有着很大影响，合适的观测矩阵应该在尽可能低的观测维数下，由一种重构算法，恢复出尽可能纯净的语音信息，同时又能去掉了大量噪声。即要在观测值M尽可能小的情况下达到对原始信号x较好的去噪效果，以此来提高最后的识别率。

观测矩阵Φ分为随机观测矩阵和确定性观测矩阵。随机观测矩阵与大多数变换基矩阵不相关，很大概率满足RIP条件，比较容易构造。但在实际应用中，存在不确定性。确定性矩阵虽然不存在上述问题，但构造比较困难。目前在压缩感知中普遍采用随机观测矩阵对信号进行低维投影，常用的有Gauss分布随机矩阵，Bernoulli分布随机矩阵，Fourier矩阵，Toeplitz矩阵和Hadamard矩阵，文献[9]讨论了这些随机矩阵的性能，如图3所示，从图中可以看Hadamard矩阵性能最优。

图3　五种随机矩阵性能比较

1.4改进OMP重构算法

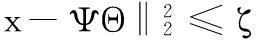
(2)

式中ζ为重构信号与带噪语音信号x之间的残差。当重构信号越接近x中的纯语音信号时重构性能越好，而不是让重构信号逼近x。

OMP算法依据残余信号r与原子库D=ΦΨ中原子内积由大到小恢复信号的，其实也是根据信号分量的重要性程度来决定迭代恢复的次序。可以把带噪语音信号分为三个部分：纯净部分、带噪部分和噪声部分，那么，语音信号的重构就可以划分为以下三个阶段：(1) 纯语音信息的迭代恢复；(2) 带噪语音信息的迭代恢复；(3) 噪声信息的迭代恢复。要实现语音增强，需要控制迭代的次数。

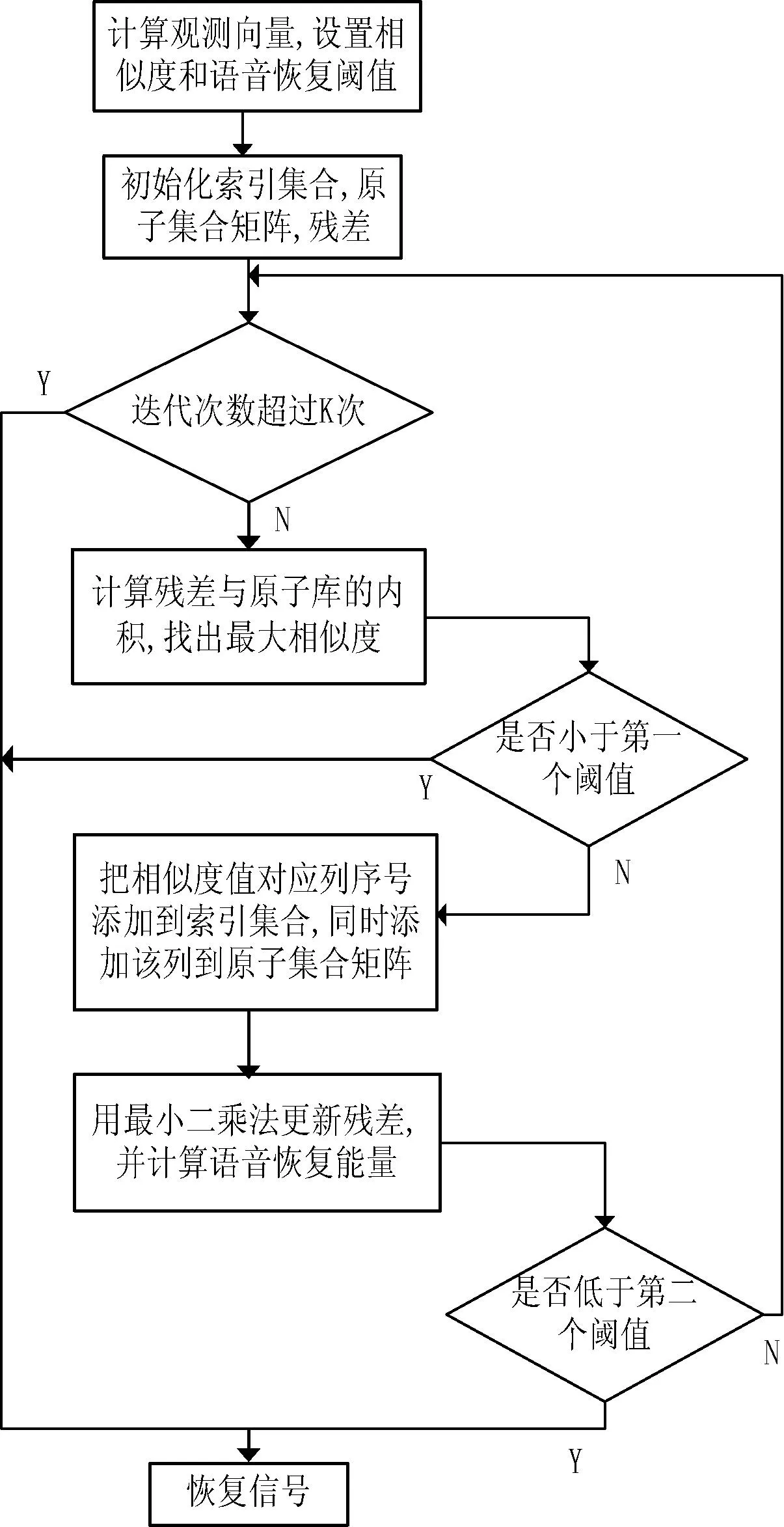
图4　改进OMP算法流程图

2Gammatone特征提取

Gammatone滤波器能很好地模拟人耳基底膜的分频特性，本文通过该滤波器组提取特征参数GFCC。先对带噪信号作预处理(预加重、分帧和加窗)和压缩重构，然后将恢复的信号通过一组64通道的Gammatone滤波器组，其中心频率在50～8000Hz之间[11]，时域表达形式如式(3)：

g(f,t)=kta-1e-2πbtcos(2πft+φ)t≥0

(3)

式中，k为滤波器增益，a为滤波器阶数，f为中心频率，φ为相位，b为衰减因子，该因子决定相应的滤波器的带宽，它与中心频率f的关系为：

b=24.7(4.37f/1000+1)

(4)

由于Gammatone滤波器的时域表达式为冲击响应函数，所以将其进行傅里叶变换就可以得到其频率响应特性。不同中心频率的Gammatone滤波器幅频响应曲线如图5所示。

图5　一组不同中心频率下Gammatone滤波器的幅频响应曲线

当语音信号通过该滤波器时，输出信号Gm(i)的响应表达式为：

(5)

式中，N=64是滤波器的通道数，M是采样之后的帧数。

这样Gm(i)就构成了一个矩阵，它的每一列称为Gammatone特征系(GF)[12]，一个GF特征矢量由64个频率成分组成。由于相邻的滤波器通道有重叠的部分，GF特征矢量相互之间存在相关性。为了减小GF特征矢量的维度及相关性，这里对每一个GF特征矢量进行离散余弦变换(DCT)，具体表示为：

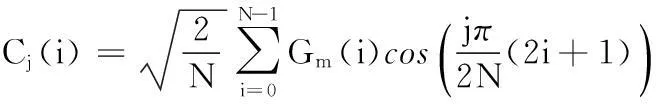
(6)

将系数Ci(j)称为GFCC系数。图6为语音段“发布”的GFCC特征系数，其主要特征体现在低维(前30维)上。在实际的说话人识别系统中，由于计算量大，并非取全部维数的GFCC系数。文献[13]证明，主成分分析PCA(principalcomponentsanalysis)技术可以把64维GFCC系数，按累积贡献率不小于85%的准则，降到26维。降维后的GFCC特征参数表示为：

(7)

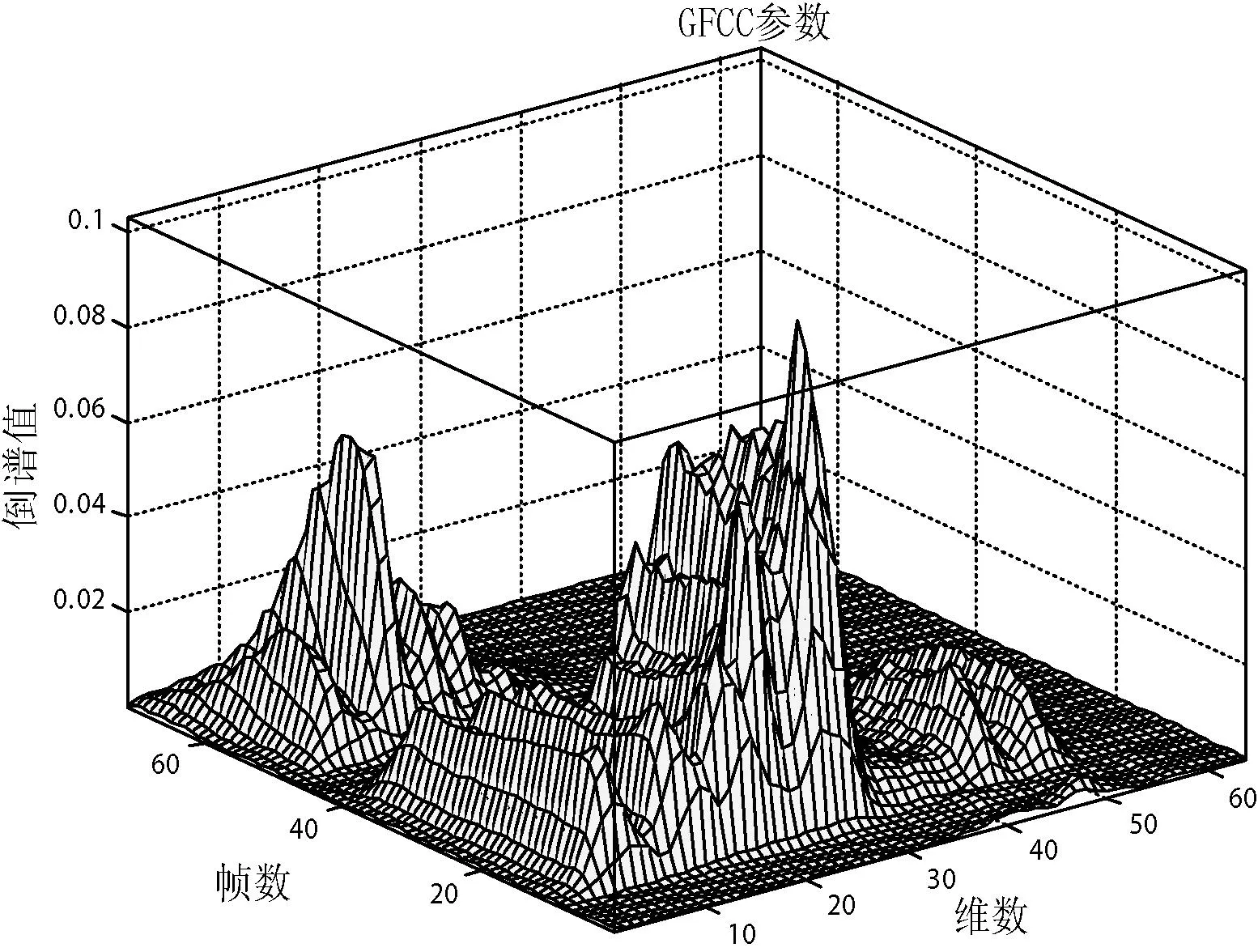
图6　语音段“发布”的GFCC特征系数

3实验结果与分析

实验所用的语音库是用麦克风录制的，语音采用的是单声道，8KHz的采样频率，16bit量化。该语音库由20人录制，每个人录制10段语音，时长分2～5s不等，将每个人的4段语音作为训练样本集，用高斯混合模型对其训练，另外6段语音作为测试样本集。混入噪声选自NOISEX-92标准噪声库中的white噪声和babble噪声，信噪比分别为-10、-5、0、5和10dB。采用的识别方法是高斯混合模型(GMM)，GMM的混合数是16。仿真结果如图7所示。

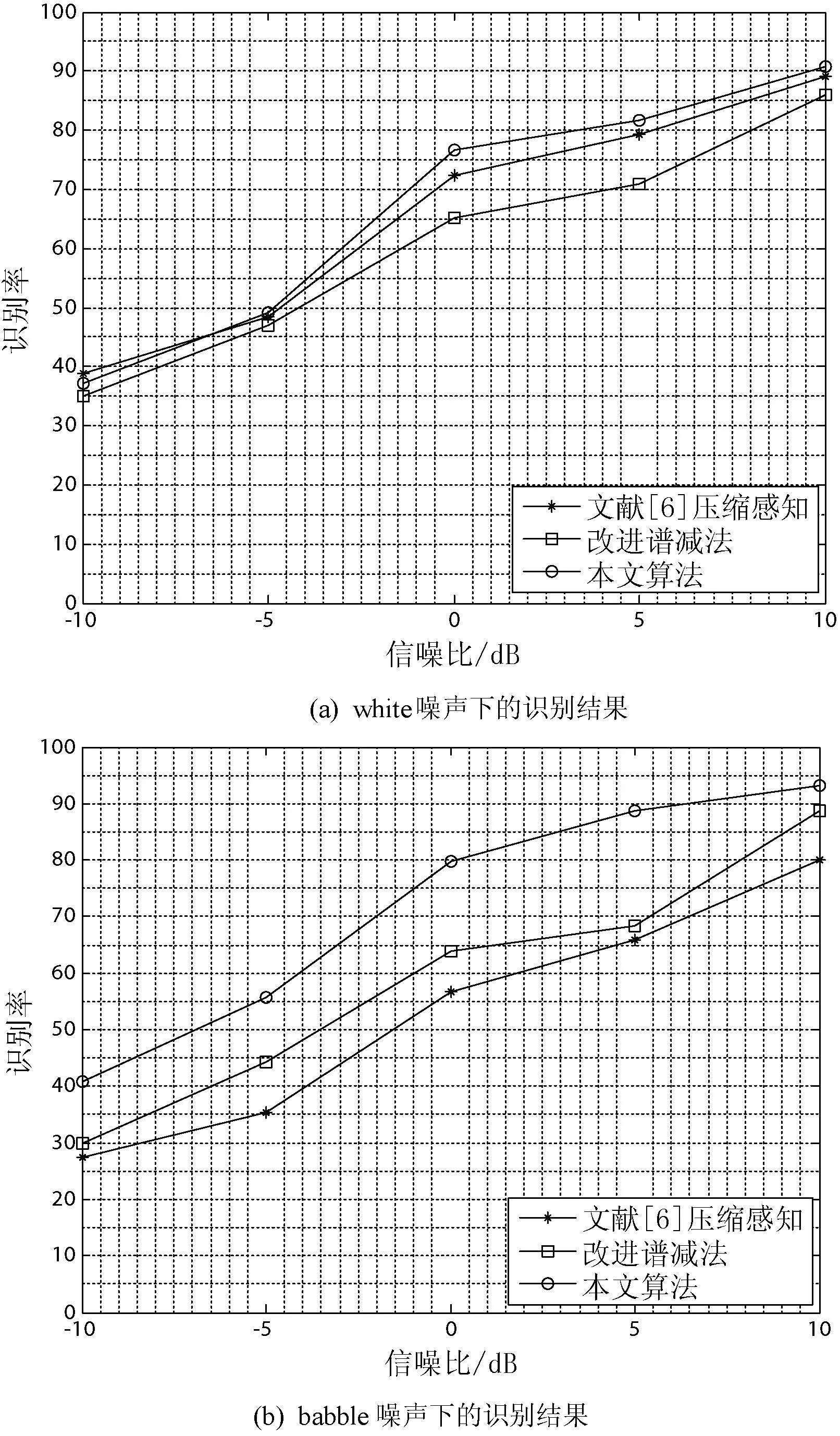
图7　仿真实验结果

为了获得经本文算法处理后语音的主观听觉感受，采用MOS评分法，接受10位听众的听觉感受测试，听众根据处理后语音的清晰度、可懂度和噪声情况综合给出评分，然后记录不同算法处理后的MOS均分，如表1所示。

表1　主观MOS评分比较

从图7和表1中可以看出，本文算法的识别率和MOS评分要高于文献[6]的压缩感知方法以及一般的语音去噪增强算法，尤其在人声背景噪声环境下，本文算法抗噪能力并未下降，凸显出本文算法的优越性。

4结语

语音信号作为一种典型的非平稳性信号，容易受到噪声的干扰。本文给出了一种基于改进压缩感知的说话人识别抗噪算法，先对带噪语音信号作预处理，然后压缩重构，将重构恢复的语音信号通过Gammatone滤波器组提取特征参数GFCC，最后在GMM模型中识别。实验结果表明，本文算法的识别率、鲁棒性及主观感受都优于传统的语音增强识别算法。GFCC特征参数能很好地模拟人耳基底膜特性，降低加性噪声的影响；改进的压缩感知能降低人声背景噪声的干扰，增加了该算法在更多背景噪声环境下的适应性。然而，OMP重构时每次迭代都要用最小二乘法估计残差，随着迭代次数的增加，原子集合矩阵不断扩大，矩阵求逆的运算量和重建所需的时间也相应增加。在短时间内进行说话人识别时，识别算法还需进一步改进。因此，如何优化本文算法，减少计算量，实现短时识别将是下一步研究的重点。

参考文献

[1]MarcoFDuarte,YoninaCEldar.StructuredCompressedSensing:FromTheorytoApplications[J].Transactiononsignalprocessing,2011, 59(9):4053-4085.

[2] 刘振.基于压缩感知的随机调制雷达信号处理方法与应用研究[D].湖南:国防科技大学研究生院,2013.

[3] 杜衍震,孙丰荣,李凯一,等.一种合成聚焦的便携式B型超声成像方法[J].计算机工程,2014,40(1):246-249.

[4]MorenoRG,MauricioMG.DCT-Compressivesamplingappliedtospeechsignals[C]//21stInternationalConferenceonElectricalCommunicationsandComputers.SanAndresCholula,Puebla,Mexico,2011:55-59.

[5] 季云云,杨震.基于自相关观测的语音信号压缩感知[J].信号处理,2011,27(2):207-214.

[6] 周小星,王安娜,孙红英,等.基于压缩感知过程的语音增强[J].清华大学学报,2011,51(9):1234-1238.

[7] 张长青,陈砚圃.离散余弦小波包变换及语音信号压缩感知[J].声学技术,2014,33(1):35-40.

[8]ThongTDo,LuGan,NamHNguyen,etal.FastandEfficientCompressiveSensingUsingStructurallyRandomMatrices[J].IEEETransactionsonSignalProcessing,2012,60(1):139-154.

[9] 李小波.基于压缩感知的测量矩阵研究[D].北京:北京交通大学,2010.

[10]LinghuaChang,JwoyuhWu.AnImprovedRIP-BasedPerformanceGuaranteeforSparseSignalRecoveryviaOrthogonalMatchingPursuit[J].IEEETransactionsonInformationTheory,2014,60(9):5702-5715.

[11] 王玥,钱志鸿,王雪,等.基于伽马通滤波器组的听觉特征提取算法研究[J].电子学报,2010,38(3):525-528.

[12]XavierValero,FrancescAlias.GammatoneCepstralCoefficients:BiologicallyinspiredFeaturesforNon-SpeechAudioClassification[J].IEEETransactionsonMultimedia,2012,14(6):1684-1689.

[13]HarunUguz.Atwo-stagefeatureselectionmethodfortextcategorizationbyusinginformationgain,principalcomponentanalysisandgeneticalgorithm[J].Knowledge-BasedSystems,2011,24(7):1024-1032.

[14] 茅正冲,王正创,龚熙.一种低信噪比下的说话人识别算法研究[J].计算机应用与软件,2014,31(12):218-220,252.

A SPEAKER RECOGNITION ANTI-NOISE ALGORITHM BASEDONIMPROVEDCOMPRESSIVESENSING

Mao ZhengchongGong Xi

(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi 214122,Jiangsu,China)

AbstractCompressive sensing (CS) is a method based on signal sparseness, and can efficiently extract useful information from signals. In this paper we present a speaker recognition anti-noise algorithm, which is based on improved compressive sensing, according to the different sparseness between speech signal and interfering noises in discrete cosine transform (DCT) area. We set correlation threshold and speech recovery threshold when reconstructing speech signals with orthogonal matching pursuit algorithm, this can not only restore speech signal effectively, but also realises the speech enhancement. Then through Gammatone filter bank we process the restored speech signal and extract feature parameter GFCC. Simulation experiment is conducted in Gaussian mixture model recognition system, experimental result shows that this algorithm obviously improves the recognition rate and robustness when being applied to speaker recognition and anti-noise system.

KeywordsCompressive sensingOMPGFCCAnti-noise algorithmRecognition rate

收稿日期：2015-01-05。国家自然科学基金项目(60973095)；江苏省自然科学基金项目(BK20131107)。茅正冲，副教授，主研领域：机器人视听觉识别。龚熙，硕士生。

中图分类号TP391.4

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.038