GA-BP网络在凿岩防卡阀推进压力预测中的应用

马威，　马飞，　郭荣，　耿晓光

(北京科技大学 机械工程学院, 北京　100083)



GA-BP网络在凿岩防卡阀推进压力预测中的应用

马威，马飞，郭荣，耿晓光

(北京科技大学 机械工程学院, 北京100083)

摘要：分析了凿岩钻车防卡阀的结构和工作原理，利用某采石场原始卡钎数据，建立了防卡阀BP神经网络模型。基于遗传算法理论对BP神经网络模型进行了结构拓扑优化和训练，建立了GA-BP网络模型。分析结果表明，BP神经网络模型和GA-BP网络模型均可以较好地预测卡钎时防卡阀的推进压力，但GA-BP网络模型具有更高的预测精度、非线性映射和网络性能。

关键词：凿岩； 防卡阀； 推进压力； BP神经网络； 遗传算法

网络出版地址：http://www.cnki.net/kcms/detail/32.1627.TP.20160705.1500.011.html

0引言

凿岩钻车在高速凿岩时，常有卡钎事故发生，卡钎现象是影响凿岩效率和凿岩质量的重要因素。所以，有效的防卡钎装置对液压凿岩钻车具有非常重要的意义。为此，一些学者对凿岩钻车的防卡钎系统展开了研究。吴万荣等[1]通过对钻孔偏斜的影响因素及力学特征的分析，建立了钻头偏载的力学模型，揭示了凿岩过程钻孔偏斜的机理，提出了控制钻孔偏斜的推进力控制方案。罗生梅等[2]针对3种不同的卡钎现象，提出了基于参数变化率和绝对变化量的综合卡钎判定方法。赵宏强等[3]利用模糊控制理论，通过AMEsim与Simulink联合仿真，验证了根据回转压力信号的变化自动控制推进力大小的可行性。

综上，目前防卡钎研究主要侧重于防卡钎系统的整体动态响应特性研究，在一定程度上解决了凿岩卡钎问题，但由于防卡阀为涉及机械、流体、控制等多个学科领域的复杂物理系统，其可靠性取决于多个物理场的耦合作用，并且非线性较强。因此，建立防卡阀模型，确定影响其性能的关键因素及其影响规律，对防卡阀设计至关重要。

针对凿岩系统中防卡阀相关研究的不足，笔者首先现场实测回转和推进压力曲线，在复杂多变的岩石工况下捕捉卡钎现象，并获取相应的压力信号；然后建立了防卡阀BP神经网络模型和遗传算法优化BP(GA-BP)神经网络模型，分析了影响防卡阀性能的因素，对实验数据进行了训练和测试；最后，对2种模型的实验结果对比分析，验证了GA-BP网络比BP神经网络具有更高的预测精度、非线性映射和网络性能。

1防卡阀结构和防卡钎系统原理

防卡钎系统原理[4]如图1所示，防卡阀的结构及原理如图2所示。

1-低压推进溢流阀；2-高压推进溢流阀；3-发动机；

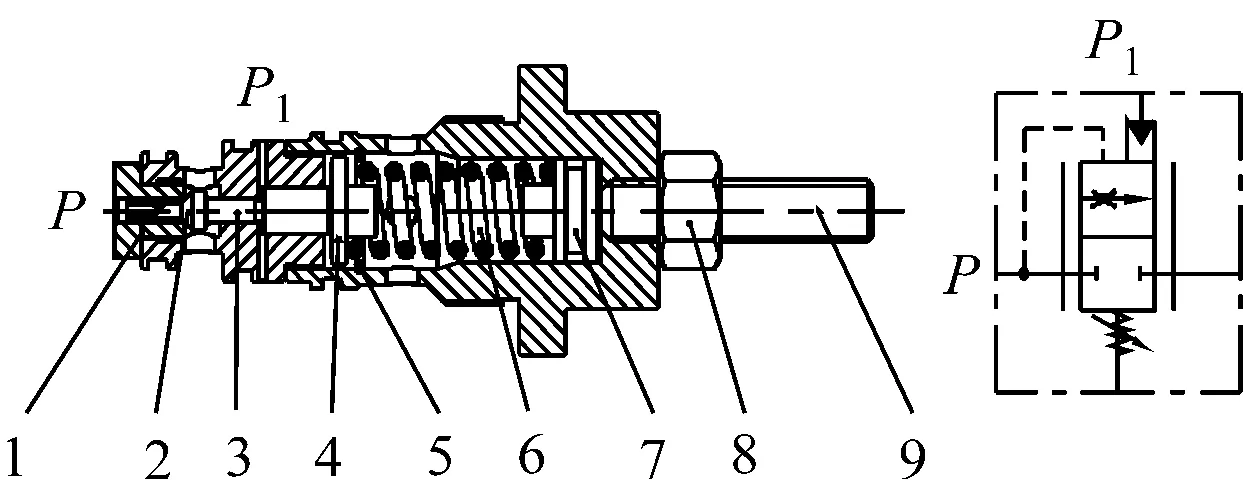
1-阀座；2-阀芯；3-顶杆；4-簧座；5-挡圈；

在钻孔时，如果回转压力P1超过防卡阀的设定值，则防卡阀的阀芯、顶杆和簧座将会克服弹簧预紧力而被推动，阀芯移动的最大距离由挡圈来限制，此时，控制推进的油压P就会部分通过防卡阀的节流腔从低压推进溢流阀流出，推进压力和速度相应降低，正常情况下就会使回转压力下降，并保持在一个相对稳定的数值。根据回转压力超过设定值的程度不同，防卡阀的阀芯在关闭和全开位置变动，从而使推进压力在高压推进和低压推进之间平稳变动。根据岩石的具体情况，可通过旋转调节螺钉来改变弹簧的预压缩量，设定防卡阀的临界回转压力。

2样本数据采集和训练

现场实验主要考察推进器的推进压力随孔内因素变化时的反应特性。由于BP神经网络模型是建立在大量训练样本基础之上，因此，训练样本应该足够大。将防卡阀应用在某国产露天凿岩钻车上，现场实验时, 在推进油缸的进出油口、凿岩机回转发动机的进出油口分别安装压力传感器，经采集模块连接至计算机测试软件，测量在钻孔工作过程中各处压力的变化情况。

实验在某采石场进行，测试了钻孔过程中多个炮孔的有关数据。图3、图4为捕捉到卡钎迹象时的推进和回转压力训练和测试曲线。通过局部放大图可以看到，推进压力随回转压力的增大而减小，当卡钎现象解除后，推进和回转即以正常压力值进行。

(a) 完整凿岩过程

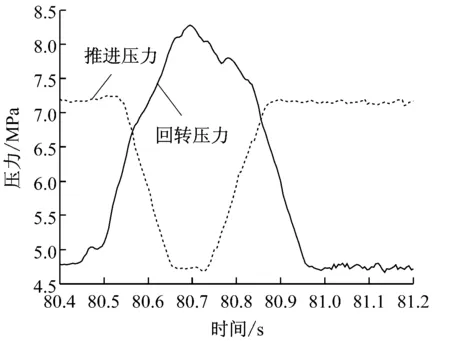
(b) 卡钎瞬间

实验测量的训练和测试样本分别见表1和表2。

3防卡阀BP神经网络模型

将卡钎影响因素作为网络输入层，卡钎反馈参数作为网络输出层，在网络的输入层与输出层之间确定合理的隐含层与连接权，就可以建立起防卡钎系统的BP神经网络模型。

(a) 完整凿岩过程

(b) 卡钎瞬间

时间/s回转压力/MPa推进压力/MPa80.404.78557.197380.454.83867.168980.505.09687.233180.556.36397.034280.607.14855.908780.657.94054.800280.708.26374.732180.757.87915.003280.807.68785.9412时间/s回转压力/MPa推进压力/MPa80.857.10466.805680.906.01637.193980.954.90727.152681.004.73047.141681.054.79057.137481.104.71097.140481.154.72557.141481.204.71757.168681.254.74507.1117

3.1BP算法

BP算法将学习过程划分为2个阶段，即信号的正向通信阶段和误差的反向传播阶段。在正向通信阶段，信息从输入层通过隐含层到达输出层[5]。输出信号在输出侧形成，网络的权值在信息传递过程中为定值，每一层的神经元状态只影响下一层的神经元状态。如果不能在输出层得到期望输出值，那么误差信号将会反向传播。在反向传播阶段，不能满足精度要求的误差信号被每一层共享。根据误差信号动态地调整连接权值，通过正反向循环调整，使神经元之间权值保持连接。当输出信号的误差值满足精度要求时学习停止[6]。

kolmogorov定理：对于任意连续函数f：Un→Rm，f(X)=Y，假如U处于单位间隔[0,1]，那么f可以通过一个3层BP神经网络精确模拟。

表2　BP神经网络测试样本

根据kolmogorov定理，在一定范围内，用含有一个隐含层的BP网络可以完成任意n维到m维的映射[7-9]。图5为具有1个隐含层的BP神经网络模型[10]。R为输入层，S1为隐含层，S2为输出层，IW1.1为输入层的权值矩阵，LW2.1为从隐含层到输出层的权值矩阵，n1和n2为神经网络层数，b1和b2分别为隐含层和输出层的阈值，f1和f2分别为隐含层和输出层的神经元传递函数。

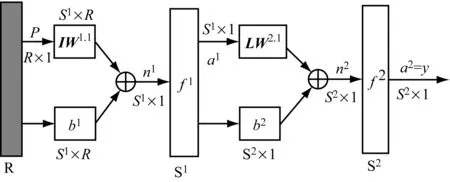
图5　具有1个隐含层的BP神经网络

假设输出层神经元j在时刻t的实际输出值为yj(t)，期望输出值为dj(t)，则网络的误差函数E(t)定义如下：

(1)

式中：S2为输出层S2的神经元个数；ε为预设误差允许值，当E(t)小于ε时，训练所得的模型就是所需的网络模型。

3.2BP网络结构

BP网络包含以下3层：

(1) 输入层神经元。根据防卡阀结构和防卡钎系统原理，将回转压力作为模型的输入层。

(2) 输出层神经元。尽管大直径深孔凿岩过程中引起卡钎的因素十分复杂，但其客观因素主要是钻头推进压力和钻孔过程中岩体构造及岩石性质的变化。因此，在建立BP网络模型时，设模型的输出层为推进压力。

(3) 隐含层神经元。隐含层神经元个数没有理论上的计算公式，只能根据经验公式来计算[5]：

(2)

式中：S1，R分别为隐含层、输入层神经元个数,S1=3，4，…，11；a为1～10的常数。

隐含层神经元个数越多，网络的预测效果越好，但是隐含层神经元个数过多，就会大大增加模型的计算量，严重影响网络的收敛速度。隐含层神经元个数为8时误差最小，因此本文建构1-8-1的BP神经网络预测模型。

3.3BP网络训练和测试

因为传统的BP算法为梯度下降法，线性收敛速度比较慢，而LM(Levenberg-Marquardt)算法对传统BP算法进行了改进，具有全局二阶收敛性(只有当Hesse矩阵的二阶项趋于零时，才能应用LM算法)，运算速度更快。因此，选择TRAINLM作为网络的训练函数。

训练过程的均方差(Mean Squared Error，MSE)曲线如图6所示。在训练次数为535次时，均方差达到10-3。均方差越小，预测值就越接近期望值，但相应的训练次数会增加，影响网络训练的速度，甚至陷入死循环。结合预测结果进行综合考虑，均方差选为10-3，既可保证预测结果的准确性，又不会影响训练过程的快速性，具有较高的灵敏度。

图6　训练过程的均方差曲线

训练过程存在一定的随机性，需要对训练结果进行检测以保证其准确性，网络训练输出值和期望值的线性回归分析如图7所示，相关系数为0.999 36，拟合度越接近1，表明网络输出值对期望值的追踪效果越好。

4GA-BP网络

遗传算法是一种随机搜寻算法，参考自然选择、生物进化的遗传机制，解决非线性搜寻的优化问题[11-12]。

图7　网络训练输出值和期望值的线性回归分析

4.1GA-BP网络实现步骤

GA-BP网络分为2部分：第1部分是将遗传算法嵌入神经网络，在网络的权值范围内搜寻最优个体；第2部分把GA搜寻到的最优个体作为网络的初始权值和阈值，然后直接利用BP算法训练网络。具体实现步骤如下：

(1) 编码和初始化。GA-BP神经网络的主要目标是优化神经元之间的连接权值和阈值。每个权值和阈值直接用实数表示，相比于二进制编码，实数编码方式更加直观和精确。设种群规模为N，每个个体包含S个基因(连接权重)：S=RS1+S1S2+S1+S2。每个实数的范围设置为[-1，1]，得到初始种群P(t)。

(2) 计算种群个体的适应度值。分配初始种群的权值和阈值S到BP网络，输入信号向前传播，计算输出值和期望值之间的和方差(Sum of Squared Errors，SSE)，适应度函数可以表示为SSE的倒数：

(3)

式中：sol为种群的任意个体；oi为第i个输出神经元的实际输出；yi为第i个输出神经元的期望输出；no为输出神经元的个数。

实际输出和期望输出之间的差异越小，适应度函数的值越大。

(3) 选择策略。通过计算种群中每个个体的适应度，将个体分类。根据适应度大小顺序，决定个体被选择的可能性，也就是比例选择法：

(4)

式中：n为神经网络层数；fi为第i个神经元的传递函数。

比例选择法保证了拥有较大适应度值的个体优先被选择，但还是有一些小适应度值的个体被选择。

(5)

(6)

式中：α为每对父本个体产生的随机数，0<α<1，α≤Pc，Pc为每对父本个体的交叉速率。

(6) 产生新种群。在种群P(t)中插入新的个体，产生新的种群P(t+1)。将新种群个体的连接权值赋给神经网络，计算新个体的适应度，如果达到预设值，就进入下一步骤，否则继续进行遗传操作。

(7) 给BP网络分配初始权值。将GA搜寻到的最优个体解码，分配给相应BP网络的初始连接权值，然后继续用BP算法训练网络，直到和方差达到设定精度或达到最大迭代数，算法终止。

4.2GA-BP网络模型设计

4.2.1参数设置

为便于比较，设置GA-BP网络模型的参数与BP网络相同。初始学习率为0.08，输入层到隐含层的传递函数为tansig，隐含层到输出层的传递函数为purelin，训练函数为trainlm。

GA-BP网络的权值用实数表示，用实数编码法编码。由于变量本身是实数，所以可不通过解码，直接计算目标值和适应度值，以加快搜索速度[13]。每一个连接权值通过一个实数直接表示，通过对所有权值和阈值编码而获得的位串称为个体，sol=[s1，s2，…，sL]。对应于个体的每个权值和阈值被称为基因。所有权值、阈值结合Matlab命令W1,B,W2,S形成实数编码遗传算法的染色体，其长度为L=nin+nno+n+no。本文有1个输入层单元，3个隐含层单元，1个输出层单元，加上隐含层和输出层的阈值，每个个体长度为10，每个实数的范围是[-1，1]。

遗传算法在进化搜索过程中不用外部信息，只基于适应度函数，所以适应度函数的选择很重要，直接影响着收敛速率和寻最优解的能力。目标函数是网络的和方差，为了获得它的最小值，适应度函数采用误差函数的倒数。选择函数采用基于正态分布的序列选择函数，交叉函数采用算术交叉，变异函数采用非均匀变异。

如果最优个体对应的适应度函数的值满足精度要求，或达到设置的迭代次数，或最后改变的平均适应度值的范围小于某个特定值，就结束训练；同时，设置拥有最大适应度值的个体作为最优解。否则，继续循环，对现有父本和后代重新排序，选择拥有最大适应度值的N个个体作为下一代；然后计算适应度并再次训练，直到满足终止条件。

4.2.2BP网络训练

解码从遗传算法中获得的最优解，并分配到还未训练的BP网络中作为初始权值，然后根据BP算法，输入训练样本进行网络训练和学习，计算输出值和期望值之间的误差。如果误差大于精度要求，则转为反向传播进程，返回误差信号。同时，根据每一层误差的大小，调整权值和阈值，直到误差小于设定值，或达到预设的训练次数，终止BP算法。保存训练好的隐含层权值和阈值，作为新的初始权值和阈值，然后对测试样本进行仿真。

图8为遗传算法的适应度变化曲线，当遗传算法收敛时，适应度值随着遗传代数的增加而增大。

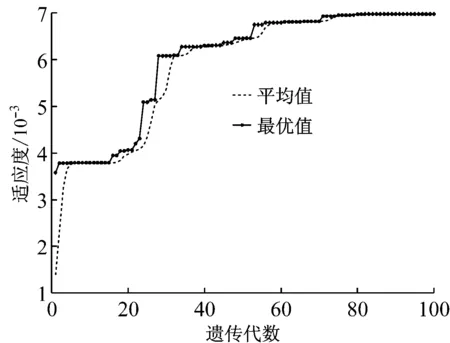
图8　遗传算法的适应度变化曲线

图9为遗传算法的和方差变化曲线，当遗传算法收敛时，SSE随着遗传代数的增加而减小。

图9　遗传算法的和方差变化曲线

5性能分析

图10为推进压力的真实值、BP神经网络模型预测值和GA-BP预测值。从图10可以看出，BP神经网络模型和GA-BP网络模型均可以较好地预测卡钎时防卡阀的推进压力。

图10　真实值、BP预测值和GA-BP预测值

为了评价BP神经网络模型和GA-BP网络模型的预测精度，采用以下误差公式[14]：

和方差公式：

(7)

均方差公式：

(8)

平均绝对误差(Mean Absolute Error，MAE)公式：

(9)

均方根(Root Mean Squared Error， RMSE)公式：

(10)

确定系数公式：

(11)

式中：SST为真实数据和均值之差的平方和。

BP神经网络和GA-BP网络对防卡阀推进压力的预测误差见表3。可以看出，通过遗传算法优化后，和方差从1.103 6减小到0.072 0，确定系数从0.945 0增大到0.996 4，说明GA-BP神经网络的自学习能力要强于没有经过优化的BP神经网络，具有相对较高的预测精度、非线性映射和网络性能。

表3　BP神经网络模型和GA-BP网络模型的预测误差

6结语

介绍和分析了凿岩防卡阀和防卡钎系统的工作原理，通过现场实测回转和推进压力曲线，在复杂多变的岩石工况下捕捉卡钎现象，并获取相应的压力信号，建立了防卡阀的BP神经网络模型。训练和测试结果表明，隐含层神经元个数取8时，BP神经网络模型误差最小，在训练次数为535次时，均方差达到10-3的要求。建立了防卡阀的GA-BP网络模型，与没经过优化的BP网络模型相比，和方差从1.103 6减小到0.072 0，确定系数从0.945 0增大到0.996 4。分析结果表明，BP神经网络模型和GA-BP网络模型均可以较好地预测卡钎时防卡阀的推进压力，但GA-BP模型网络具有更高的预测精度、非线性映射和网络性能。

参考文献：

[1]吴万荣,魏建华,张永顺,等.大直径深孔凿岩钻孔偏斜的机理及其控制方案[J].中国有色金属学报,2001,11(1):153-156.

[2]罗生梅,张宏林,斯建刚,等.液压凿岩机的自动防卡钎控制方案[J].兰州理工大学学报,2009,35(3):33-38.

[3]赵宏强,郭艳,吴双斌.基于模糊控制的潜孔钻机推进回转系统仿真[J].计算机仿真,2011,28(8):159-162.

[4]马威,马飞,周志鸿.基于AMESim的凿岩钻车防卡阀的建模与仿真分析[J].矿山机械,2014,42(11):17-21.

[5]XIE Z,DU Q,REN F,et al.Improving the forecast precision of river stage spatial and temporal distribution using drain pipeline knowledge coupled with BP artificial neural networks: a case study of Panlong River,Kunming,China[J]. Nat Hazards,2015,77(2):1081-1102.

[6]王书涛,陈东营,侯培国,等.基于荧光光谱技术和GA-BP神经网络的对羟基苯甲酸甲酯钠含量的测定[J].光谱学与光谱分析,2015,35(6):1606-1610.

[7]贺志勇,郑伟.基于BP神经网络的深基坑变形预测[J].华南理工大学学报(自然科学版),2008,36(10):92-96.

[8]王吉权.BP神经网络的理论及其在农业机械化中的应用研究[D].沈阳:沈阳农业大学,2011.

[9]段宝福,张猛,李俊猛.逐孔起爆震动参数预报的BP神经网络模型[J].爆炸与冲击,2010,30(4):401-406.

[10]ZHAO Ying,NAN Jun,CUI Fuyi, et al. Water quality forecast through application of BP neural network at Yuqiao reservoir[J].Journal of Zhejiang University SCIENCE A,2007,8(9):1482-1487．

[11]LI C,YANG Z,YAN H,et al.The application and research of the GA-BP neural network algorithm in the MBR membrane fouling[J].Abstract and Applied Analysis,2014，2014(7):1-8.

[12]刘锦伟,谢雄刚,方井.基于遗传算法-BP神经网络的煤层注水效果分析[J].工矿自动化,2016,42(1):48-51.

[13]孟祥逢,鲁汉榕,郭玲.基于遗传神经网络的相似重复记录检测方法[J].计算机工程与设计,2010,31(7):1550-1553.

[14]WANG H S,WANG Y N,WANG Y C.Cost estimation of plastic injection molding parts through integration of PSO and BP neural network[J].Expert Systems with Applications,2013,40(2):418-428.

Application of GA-BP neural network in boost pressure forecast of anti-jamming valve used in rock drilling

MA Wei,MA Fei,GUO Rong,GENG Xiaoguang

(School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Abstract:Structure and working principle of anti-jamming valve on a drilling rig was analyzed, and BP neural network model of anti-jamming valve was established using original data of a quarry. The theory of genetic algorithm was utilized to optimize and analyze BP neural model, and the GA-BP model was established. The analysis results show that both BP neural network and GA-BP network model can be used to predict boost pressure of anti-jamming valve, and the GA-BP network model has higher prediction accuracy, nonlinear mapping and network performance.

Key words:rock drilling; anti-jamming valve; boost pressure; BP neural network; genetic algorithm

文章编号：1671-251X(2016)07-0044-07

DOI:10.13272/j.issn.1671-251x.2016.07.011

收稿日期：2016-01-27；修回日期：2016-05-20；责任编辑：胡娴。

基金项目：国家自然科学基金资助项目(51274021)。

作者简介：马威(1987-)，男，江苏徐州人，博士研究生，主要研究方向为凿岩钻车控制系统等,E-mail:maweiustb@163.com。

中图分类号：TD422

文献标志码：A网络出版时间：2016-07-05 15:00

马威，马飞，郭荣，等.GA-BP网络在凿岩防卡阀推进压力预测中的应用[J].工矿自动化，2016,42(7)：44-50.