柱失效方程中荷载相关特性对承载力抗震设计可靠度的影响

蒋友宝,孙国衡,周成玉,张建仁

(长沙理工大学 土木与建筑学院，长沙 410004)



柱失效方程中荷载相关特性对承载力抗震设计可靠度的影响

蒋友宝,孙国衡,周成玉,张建仁

(长沙理工大学 土木与建筑学院，长沙 410004)

摘要：以竖向荷载和水平地震作用组合下的钢筋混凝土柱和钢柱为对象，研究了失效方程中荷载相关特性对柱承载力抗震可靠性的影响。根据现行《混凝土结构设计规范》和《钢结构设计规范》分析了不同柱弯矩轴力相关曲线的特性。结合多个框架结构实例，对比了柱失效方程中荷载相关曲线与规范考虑情形的异同。实例分析表明：水平地震和竖向荷载组合作用下，小偏压RC柱和工字型钢柱的荷载相关曲线与规范考虑的情形较为符合，均近似为负相关的直线；水平地震和竖向荷载组合作用下，大偏压RC柱的荷载相关曲线则与规范考虑的情形有较大出入，存在明显的正相关段部分。在此基础上，考虑失效方程复杂特性，依据已有的荷载和抗力变量概率模型，采用Monte Carlo法分析了水平地震和竖向荷载组合作用下柱的可靠性。结果表明：钢柱和小偏压RC柱的承载力抗震可靠度随轴压力荷载效应比值的变化幅度较小，与规范模式计算结果较接近；大偏压RC柱的承载力抗震可靠度随轴压力荷载效应比值的变化会有较大幅度波动，与规范模式计算结果差异较大；当轴压力荷载效应比值为负时，大偏压RC柱的承载力抗震可靠度会低于规范计算值较多，现行柱可靠性设计方法会偏于不安全。

关键词：结构设计；可靠度；柱抗震承载力；荷载相关曲线；荷载效应比值

中国近年接连发生了几次地震灾害，如2008年汶川地震、2010年玉树地震等。在这些地震作用下，按规范设计的不同形式柱的抗震表现差异较大。例如，一些RC框架柱出现了较为严重的破坏，甚至引发结构倒塌；而钢框架柱则表现良好，其柱端破坏轻微[1]。叶列平等[2]从地震作用下RC框架梁受力较为有利的角度对RC框架柱破坏较严重的现象进行了分析，指出由于存在着楼板加强、钢筋超配等多种因素，实际梁端抗弯承载力会提高很多，因而RC框架结构中“强柱弱梁”失效模式较难出现；而钢结构震害较轻的原因一般归为其自重较轻、强度较大和抵御地震的能力比较强[1]。除上述原因外，实际上柱抗震表现差异较大的现象还与其承载力抗震可靠性随设计参数变化的规律尚未完全揭示有关，而这一方面的分析研究工作尚未引起足够重视。

已有关于柱可靠性变化规律的研究[3-5]多是针对结构中柱仅承受竖向荷载(恒载和楼面活载等)的情形，该类分析表明，各种参数情形下按规范设计的柱的可靠性均较高。但对于柱的抗震设计，水平地震作用往往是主导性的。由于水平地震作用具有较强的随机性，柱截面上各种效应(弯矩、轴力、偏心距等)均具有较明显的随机变化特征，其失效方程将具有复杂特性[6-7]。中国现行抗震规范[8]中柱承载力抗震设计的一些系数是通过可靠度校准确定的，但在校准分析柱承载力抗震可靠性随设计参数变化的规律时，为了明确关键参数对可靠指标的影响，对复杂的失效方程进行了一定简化，即按线性失效方程考虑(如高小旺等[9]采用的计算模型)。显然，当规范考虑的线性失效方程情形与真实情形有较大差异时，上述校准得到的可靠指标值将因偏差较大而无法如实反映出柱承载力抗震可靠性随设计参数变化的规律。对于RC柱，当充分考虑偏心距的随机变异性后，柱的抗弯承载力将与其所受的轴压力相关，需根据其弯矩轴力相关曲线来建立柱的复杂非线性失效方程，进而分析其可靠性随多个参数的变化规律。相关研究[10-14]表明,采用简化线性失效方程来计算RC柱可靠度的思路往往会高估了其在大偏压失效情形下的可靠性，使得此时设计偏于不安全，这一不足存在于多国结构设计规范中。对于钢柱，Pirmoz等[15]分析了按美国钢结构规范(AISC341-05)设计的偏心支撑结构中柱的抗震可靠性，结果表明，当设计参数在大范围内变化时，柱的承载力可靠性也会低于其目标值。

笔者采用中国现行设计规范中柱的承载力计算式，分析了矩形、工形截面RC柱和工形截面钢柱弯矩轴力相关曲线的特性；并结合多个框架结构实例，研究了柱失效方程中荷载相关曲线与规范考虑情形的异同；根据已有的抗力和荷载统计参数，计算得到了柱承载力抗震可靠度随多个设计参数变化的规律。

1柱承载力计算式与可靠性设计方法说明

1.1现行柱承载力计算式

中国现行主要结构设计规范[16-17]中的柱(压弯构件)极限承载力计算公式是通过理论分析和试验研究，并考虑一定的安全保证取下限值而综合得到的。从工程应用的角度考虑，当柱各受力参数的不确定性符合规范的预期且在容许范围内变动时，采用这些承载力计算式进行设计较为安全。

1.2复杂失效方程与现行柱可靠性设计方法

如前所述，现行柱可靠性设计方法中用到的各设计系数(如抗力、荷载分项系数)值是经可靠度校准得到的。但应指出，可靠度校准时为简化分析，采用的均为线性的失效方程。

实际上，无论是大偏压RC柱、小偏压RC柱，还是钢柱，其失效方程(联合后文承载力验算式(1)～(9)和荷载效应计算式(10)、(11)易得)均是关于主要随机变量(水平荷载、竖向荷载、材料强度)的复杂非线性函数。

显然，采用简化线性失效方程进行可靠度计算是不精确的，亦无法反映出失效方程复杂特性对真实可靠性的影响。例如，文献[6]中对某大偏压RC柱的可靠度进行了对比计算，结果为：按简化线性失效方程得到的可靠指标约为2.94，而同一情形下考虑失效方程复杂特性后得到的可靠指标约为2.19，校准结果高估了约0.75。该计算结果表明：对于大偏压RC柱，现行可靠性设计方法存在偏于不安全的可能。这被认为是汶川地震中RC框架柱破坏较为严重的众多可能原因之一[13]。

为研究采用简化线性失效方程(规范模式)与复杂失效方程两种情形对应的柱可靠度之间的差异，从柱弯矩轴力相关曲线入手，分析了柱失效方程中荷载相关曲线(材料强度取为定值时的失效方程曲面)与规范考虑情形的异同。同时，为与大偏压RC柱充分比较，文中亦对小偏压RC柱、钢柱进行了分析。

2柱的弯矩轴力相关曲线特性分析

2.1矩形和工形截面RC柱承载力计算

对于对称配筋矩形截面柱，见图1，由《混凝土结构设计规范(GB 50010—2010)》[16]可知，其所能承受的N和M需满足

(1)

(2)

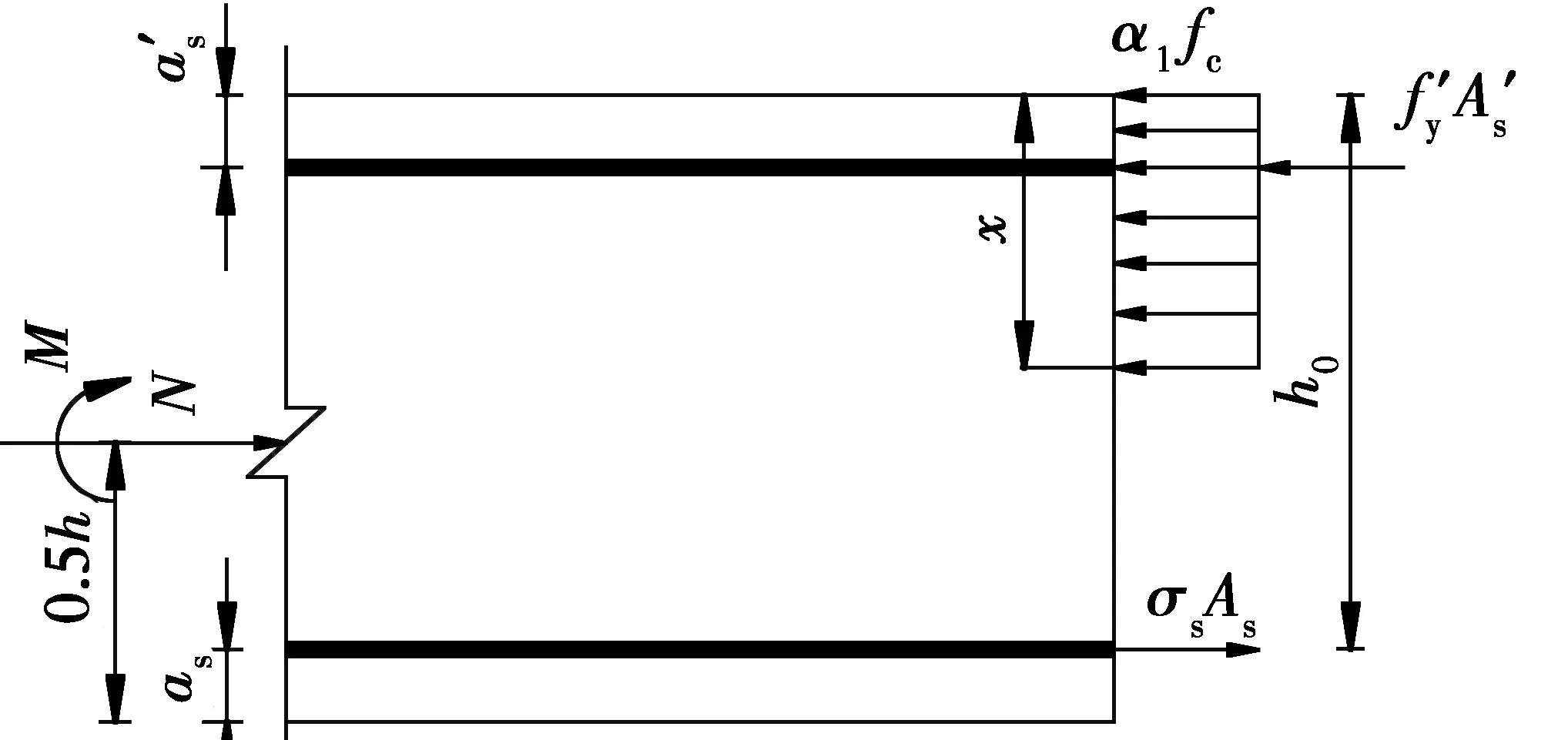
图1　矩形截面RC柱承载力计算模型Fig.1　Calculation model of capacity for RC columns with a rectangular

当为大偏压破坏时，RC柱截面受拉边纵向普通钢筋能达到屈服，此时σs=fy，fy为钢筋抗拉强度。假定钢筋拉压强度相等，因而能承受的N和M可简化为

(3)

N=α1fcbx

(4)

当为小偏压破坏时，RC柱截面受拉边纵向普通钢筋达不到屈服，此时式(1)、(2)中σs可计算为

(5)

式中：ξ为相对受压区高度；ξb为相对界限受压区高度；β1为等效矩形应力图的高度换算系数。

对于对称配筋的工字形截面柱，见图2，由《混凝土结构设计规范(GB 50010—2010)》[16]可知，当为大偏压破坏时，其承载力计算按下列要求确定。

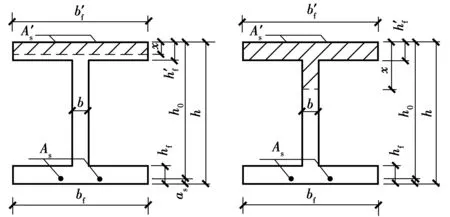
图2　工字型截面RC柱承载力计算模型Fig.2　Calculation model of capacity for RC columns with I-shaped

(6)

(7)

当为小偏压破坏时，截面受拉边纵向普通钢筋达不到屈服，因而其轴力平衡方程式(7)需改写为

(8)

式中σs仍可按式(5)计算。

2.2工形截面钢柱稳定承载力计算

由《钢结构设计规范(GB 50017—2003)》[17]可知，对于弯矩作用在对称轴平面内(绕x轴)的实腹式工形截面压弯构件，其承载力按式(9)计算。

(9)

2.3不同柱的弯矩轴力相关曲线对比

根据式(1)～(8)，可求得某典型矩形截面RC柱(4.2节算例)以及工形截面RC柱(4.3节RC柱算例)对应的M-N相关曲线；同理，按式(9)，亦可求得某典型工形截面钢柱(4.3节钢柱算例)对应的M-N相关曲线。具体结果见图3，其中，N0和M0分别为该截面所能承受的最大轴压力和弯矩。

图3　RC柱和钢柱的M-N相关曲线Fig.3　M-N interaction curves for RC columns and steel

由图3可知，工形和矩形截面RC柱的M-N相关曲线均由大偏压与小偏压两段组成，其中，大偏压段弯矩和轴力为正相关变化(弯矩随着轴力增加而增加)，而小偏压段弯矩和轴力则为负相关段。比较而言，工字形截面RC柱M-N相关曲线中正相关段的占比稍小一些。而与RC柱不同，钢柱的M-N相关曲线上弯矩和轴力均为负相关的，无正相关段部分。

3荷载相关曲线实例分析

3.1荷载相关曲线求解及与规范情形对比

设计支承多层上部结构的框架柱时，一般需考虑承受竖向荷载和水平地震作用的组合。其中，重力荷载会在柱截面上产生较大轴压力，水平地震作用则在其截面上产生较大弯矩。按线弹性分析，作用在柱截面上的弯矩M和轴力N可计算为

M=Mg+Mq=a1g+b1q

(10)

N=Ng+Nq=a2g+b2q

(11)

式中：g和q分别为竖向重力荷载和水平地震作用；a1、b1、a2和b2分别为对应的荷载效应系数。由于地震作用方向不确定，设计柱一般按组合弯矩最大来确定较不利地震作用方向，此时可能b2<0，而其余系数为正值。

对于矩形截面大偏压RC柱，由规范承载力验算式可求出给定轴力下截面所能承受的极限弯矩，即为弯矩形式的抗力，然后再考虑弯矩荷载效应，便可得到相应的失效方程，见式(12)。

(12)

将式(10)、式(11)代入式(12)，即可得到对应该失效方程的荷载相关曲线方程，见式(13)。

(a1g+b1q)=0

(13)

同理，对其他情形作同样分析，亦可得到其对应的柱失效方程，进而得到荷载相关曲线，即g-q曲线。该曲线表示的物理含义是：柱截面所能承受的最大荷载q随荷载g变化的曲线。

由于柱弯矩轴力相关曲线上存在着正相关段和负相关段部分，因此可以预见，g-q曲线上也会存在着正相关段和负相关段，见图5、图7。

现行抗震设计规范[8]在校核重力荷载和水平地震组合作用下柱可靠度水平时，采用的失效方程为

(14)

式中：R为抗力，按固定偏心距下的极限弯矩考虑，忽略其随轴力的变化；Mg、Mq分别为重力荷载与水平地震作用产生的弯矩，可按式(10)计算。由于不考虑抗力与荷载效应的相关性，式(14)将为线性方程。按式(10)将荷载变量代入可知，无论是何种设计情形，对应的荷载相关曲线均将是一条负相关直线，无正相关段，见图9。

3.2矩形截面RC框架柱

文献[6]中的RC框架模型，如图4所示，其构件参数如表1。忽略结构二阶效应，按线弹性分析可得其截面内力组合表达式。对此框架结构的柱截面1有：M=1.07g+9.41q，N=25.64g-3.06q；柱截面2有：M=1.34g+7.17q，N=17.96g+14.12q[6]。联合其承载力验算式，可求得柱截面1、截面2的g-q相关曲线，见图5。

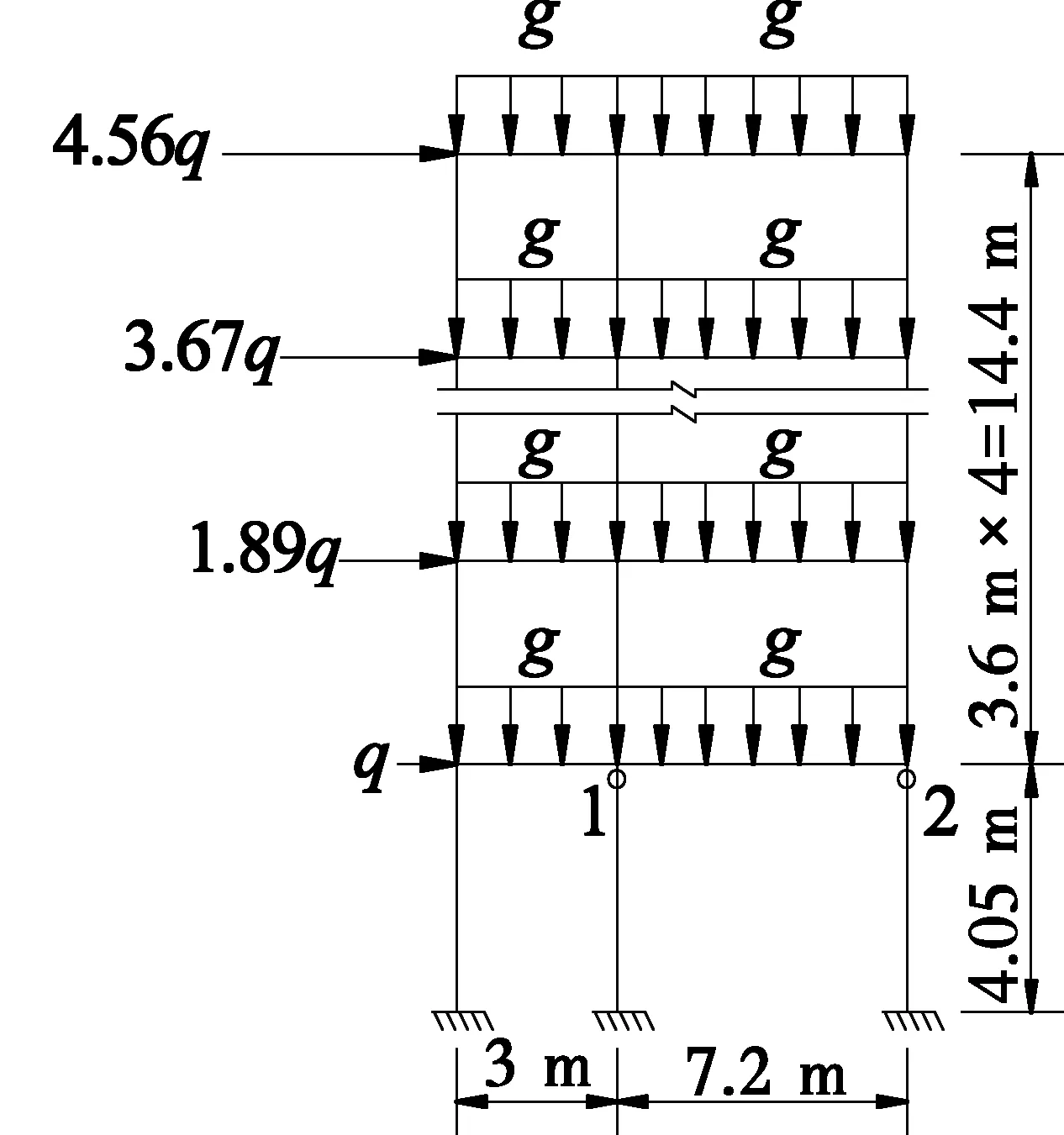
图4　采用矩形截面的RC框架结构模型Fig.4　A model of RC frame with rectangular

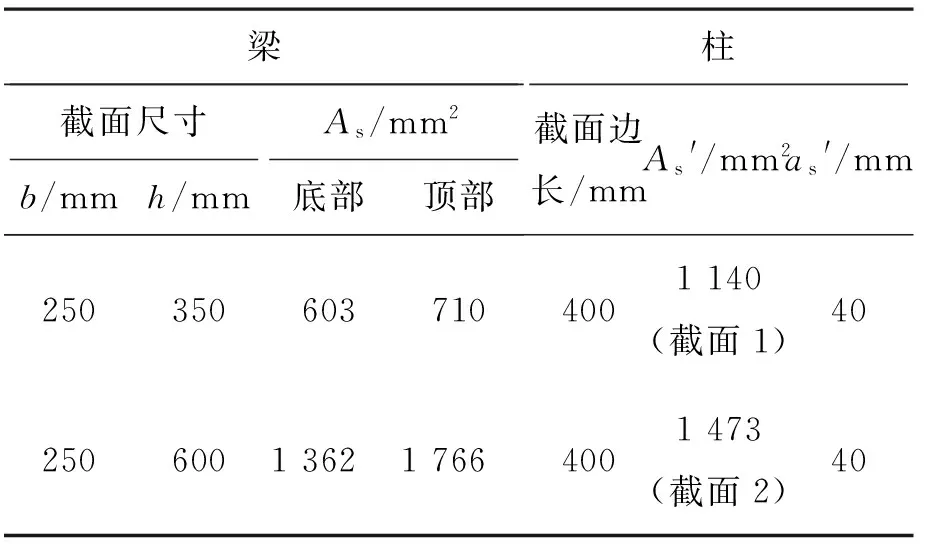
梁柱截面尺寸As/mm2b/mmh/mm底部顶部截面边长/mmAs'/mm2as'/mm2503506037104001140(截面1)40250600136217664001473(截面2)40

由荷载相关曲线的物理含义可知，当重力荷载g约为零时，图5中截面2能承受的最大地震作用q值约为30 kN；当g约为120 kN/m时，该截面能承受的最大q值约为0，亦即无地震作用下该柱能承受的最大重力荷载约为120 kN/m。对于其余截面(如图6中截面1，图8中各截面)，也可根据荷载相关曲线作相同的分析。

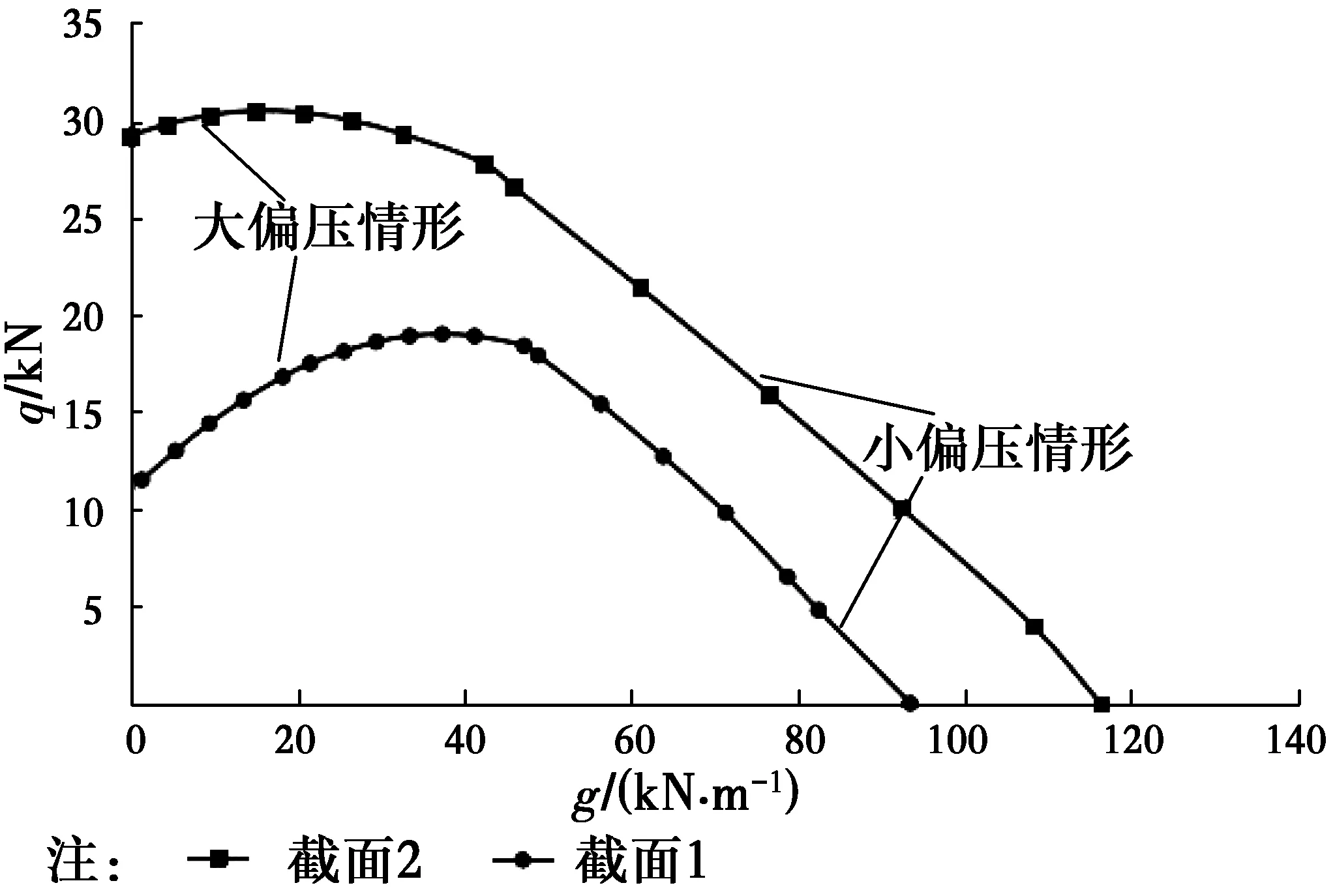
图5　RC框架柱矩形截面g-q相关曲线Fig.5　g-q interaction curves for RC frame columns with rectangular

图6　采用工形截面的框架结构模型Fig.

在小偏压的情况下，RC柱失效方程中荷载相关曲线与现行规范考虑情形较为一致，为负相关；而大偏压情形对应的荷载相关曲线则与现行规范考虑情形差异较大，有正相关段。但正相关段所占大偏压全部情形的比重则会变化，比较而言，中柱截面1正相关段曲线的占比更高一些。

3.3工形截面RC柱和钢柱

设有一框架结构模型，如图6。现假定其分别采用钢框架和RC框架结构，建立两种模型。

模型一：梁柱采用Q235钢，其截面采用工形截面，截面尺寸h×b×t×tw(高度×宽度×翼缘×腹板)。

模型二：梁柱都采用工形截面，C30混凝土、HRB335钢筋材料，各柱截面采用对称配筋，单侧配筋为2 945 mm2。

两种模型对应的截面尺寸见表2。同理，通过线弹性分析可得到两种模型中各柱截面的内力表达式。对于模型一中的柱截面1有：M=1.54g+2.57q，N=15.03g+12.62q；柱截面2有：M=5.53q，N=36.4g。对于模型二中的柱截面1有：M=1.63g+2.39q，N=17.53g+12.44q；柱截面2有：M=6.4q，N=36.93g。

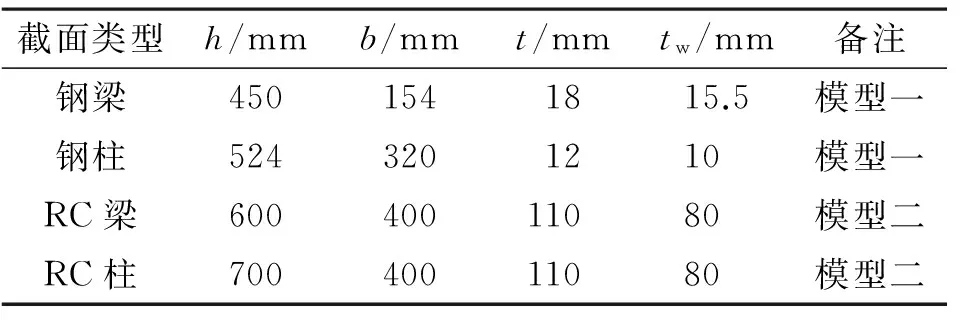
表2　采用工形截面的框架设计参数

将上述内力表达式代入承载力验算式后，可得到相应的g-q相关曲线，见图7。

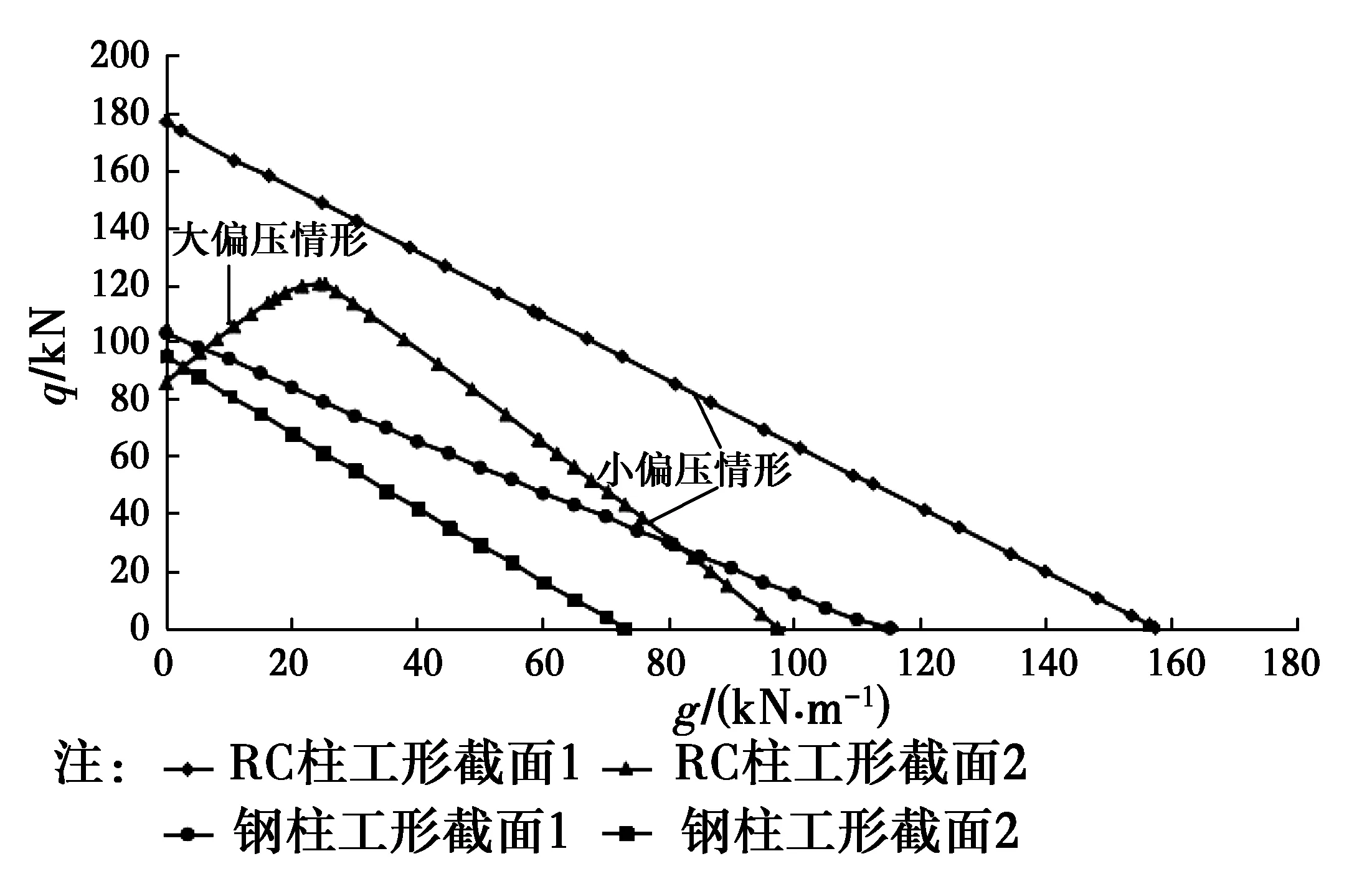
图7　工形截面RC柱和钢柱的g-q相关曲线Fig.7　g-q interaction curves for the RC column and steel column with I-shaped

由图7可知，钢柱截面的g-q相关曲线近似全为一条负相关的直线，这与现行规范设计方法所对应的荷载相关曲线较为一致。而对于工形截面RC柱，不同内力表达式对应的荷载曲线差异较大，有可能与图5中矩形截面对应的g-q相关曲线相似，既存在着负相关段，也存在着正相关段(见RC柱工形截面2)；同时,也可能会无正相关段，全为负相关的曲线，与规范设计方法对应的情形一致(由荷载效应系数所致将为小偏压破坏，见RC柱工形截面1)。

3.4验算点处荷载相关曲线分析

由文献[18]列出的统计参数模型可知，对构件可靠度影响较大的不确定性因素一般为材料强度和荷载的不确定性。在3.2节、3.3节给出的荷载相关曲线均是在材料强度取为规范设计值时获得的。实际上，按验算点处的材料强度值计算得到的荷载相关曲线更有代表性。

为此，在典型矩形截面RC框架柱(3.2节算例)中，将钢筋和混凝土强度取为验算点处的值，从而得到相应的荷载相关曲线，见图8。可知，验算点处对应的荷载相关曲线仍同时存在着正相关段和负相关段。

显然，对于小偏压RC柱和钢柱，由于其弯矩轴力相关方程本身为负相关段，且设计弯矩组合时Mg和Mq是正的值相加，因而可以预见其在验算点处对应的荷载相关曲线均为负相关。

图8　RC矩形截面柱在验算点处的g-q相关曲线Fig.8　g-q interaction curves at the check point for the RC columns with a rectangular

3.5实例分析总结

以上分析表明，对于竖向重力荷载和水平地震作用组合下的柱，当设计情形对应其荷载相关曲线的正相关段部分时，将明显不同于规范考虑的情形，见图9(a)，因而可以预见此时其设计可靠度将会与规范校核结果有较大偏差；而当设计情形对应其荷载相关曲线的负相关段时，将与规范考虑的情形较为接近，见图9(b)，因而可以预见此时其设计可靠度与规范校核结果之间的偏差较小。

图9　不同相关段情形与规范情形的对比Fig.9　Comparisons between g-q interaction curvecases with different correlation parts and cases in

4承载力可靠性分析

4.1考虑失效方程复杂特性的可靠度分析思路

由于结构形式多样、数量众多，无法对每一个结构实例完成荷载效应分析、可靠性分析，因此，可靠度校准时，一般通过引入可变荷载效应与永久荷载效应标准值的组合比例来考虑不同设计实例之间的差异。其中，荷载效应比值ρM和ρN的计算式为

ρM=b1qk/a1gk

(15)

(16)

式中：下标k表示标准值，如gk表示地震作用标准值等。若ρM=ρN，则g与q引发的偏心距相同，因此，组合作用下偏心距仍为定值，构件抗力与荷载效应无关。此时，采用线性失效方程会具有较好精度，如规范情形[9]。但实际上ρM一般为ρN的数倍以上，甚至会出现ρM为ρN百余倍的情形[19]，此时失效方程将具有复杂特性。参考文献[6]，文中ρM和ρN取值范围分别为[1.5, 5.0]和[-0.3, 0.3]。

若荷载效应比值ρM和ρN等信息已给定，则当荷载效应(弯矩和轴力)设计值确定时便能反算出其标准值，然后采用Monte Carlo方法可对荷载效应和抗力抽样，进而计算出失效概率。具体计算流程见图10。

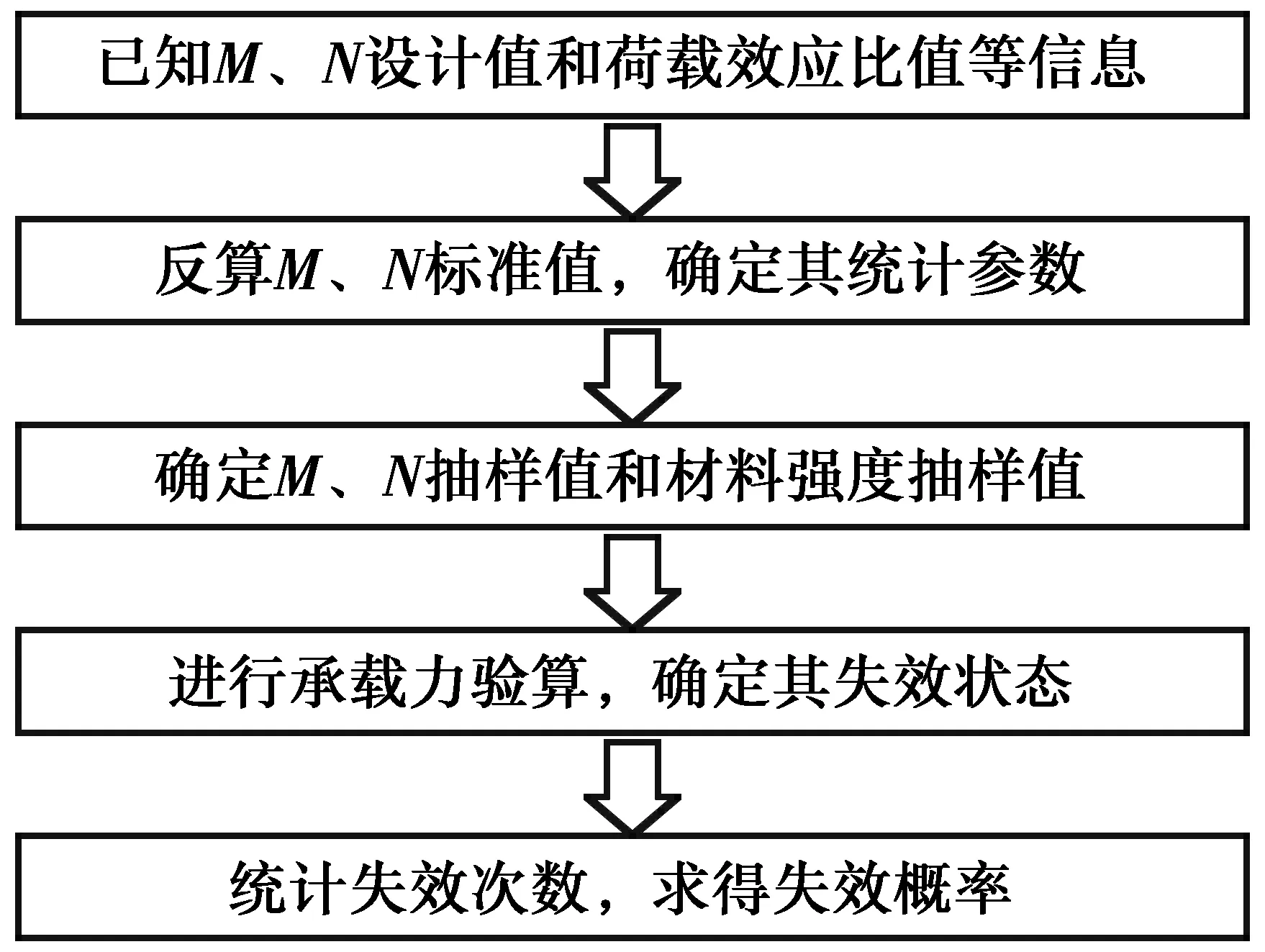
图10　考虑失效方程复杂特性的柱可靠度分析流程图Fig.10　Flowchart of reliability analysis for columns with a complex failure

可见，上述程序在计算可靠度时用到了ρM和ρN两种荷载效应比值，并考虑了它们取不同值的可能，因此，该思路摒弃了线性失效方程的简化假定，即考虑了柱失效方程的复杂特性。

4.2矩形截面RC大偏压柱

按抗震规范[8]6.2.2条文规定，RC框架柱端组合的弯矩设计值应为梁端弯矩设计值的η倍。考虑到梁柱节点受力时的力矩平衡，因而RC框架柱的弯矩和轴力的设计值为

Md=η(1.2a1gk+1.3b1qk)

(17)

Nd=1.2a2gk+1.3b2qk

(18)

式中：下标k表示标准值，下标d表示设计值，下同；1.2和1.3分别为相应的荷载分项系数；η为实现

“强柱弱梁”效应而引入的柱端弯矩增大系数，按现行抗震规范其取值为1.2、1.3、1.5和1.7。对应的设计抗力为

(19)

式中γRE为承载力抗震调整系数，一般取值为0.80。

假定某框架中有一大偏压RC柱，其截面尺寸为400 mm×400 mm，采用C30混凝土和HRB335级钢筋，单侧截面配筋率0.65%，轴压力设计值为600 kN，弯矩设计值为207.6 kN·m，则可知为大偏压设计情形。若按式(19)验算，该柱抗震承载力恰能满足要求。用于分析的变量统计参数见表3。

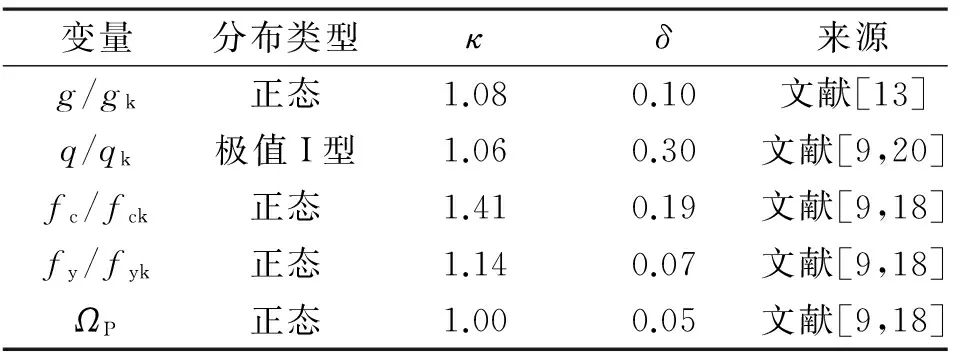
表3　RC柱可靠度分析对应的随机变量的统计参数

注：κ=平均值/标准值，δ为变异系数，下同。

计算得到的可靠度结果见表4。由表4可知，当ρN在[-0.3, 0.3]内变化而ρM一定时，考虑失效方程的复杂特性后，该大偏压RC柱可靠指标会有较大幅度的变化，且与式(14)所示的抗震规范模式计算结果有较大差异，说明规范模式结果有较大误差。

对典型情形下的验算点位置进一步查验表明，它们均位于荷载相关曲线的正相关段上。这与规范考虑情形差异较大，见图9(a)。因此，可以预见规范模式所得可靠指标将与上述结果有较大偏差。最终，计算结果证明了这点。另外，当轴力荷载效应比值为负时，规范模式将会高估可靠性较多，这表明现行柱可靠性设计方法偏于不安全。

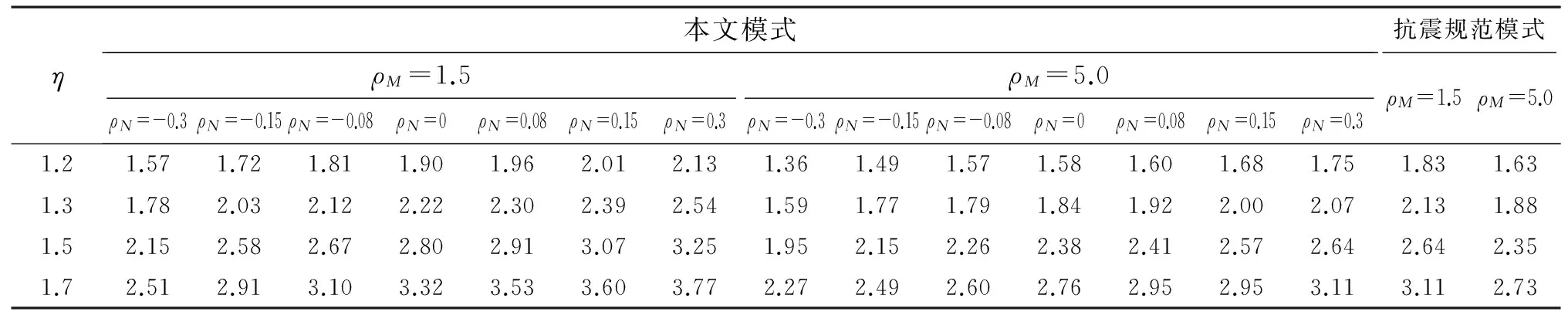
表4　某大偏压RC柱可靠指标β随ρN、ρM和η的变化

4.3矩形截面小偏压RC柱

对矩形截面小偏压RC柱进行承载力抗震验算时，其设计弯矩可计算为

(20)

(21)

假定仍选4.2节中的RC柱为分析对象，设柱的轴压力设计值改为1 700 kN，弯矩设计值改为238.2 kN·m，其余参数不变，则可知此时为小偏压设计情形，当按式(20)和式(21)进行抗震承载力验算，该柱恰能满足要求。

对于此小偏压RC柱，采用Monte Carlo方法计算，可求得其可靠度随ρN、ρM和η的变化，见表5。

表5　某小偏压RC柱可靠指标β随ρN、ρM和η的变化

由表5可知，当ρN在[-0.3, 0.3]范围内变化而ρM一定时，小偏压RC柱可靠指标变化幅度不大；计算结果也与抗震规范模式对应的可靠度结果相差较小，说明在此情形下规范模式具有较好适用性。

4.4工形截面钢柱

钢柱的承载力一般多由其稳定承载力控制，与式(9)对应的承载力抗震验算式为

(22)

式中γRE取值为0.80。与混凝土框架柱不同，钢框架中为预期实现“强柱弱梁”效应，采用的节点处梁柱弯矩验算式为

(23)

式中:∑Wpc、∑Wpb分别为交汇于节点的柱和梁的塑性截面模量；fyc、fyb分别为柱和梁的钢材屈服强度；N为地震组合的柱轴力；Ac为框架柱的截面面积；η为强柱系数，一级取1.15，二级取1.10，三级取1.05，四级取1.0。

为考虑柱弯矩轴力相关曲线特性对其承载力抗震可靠性的影响，同时为与RC柱对比，假定仍按式(17)、(18)计算钢柱弯矩和轴力设计值，其中η按抗震等级不同取值1.0～1.15，然后仍按式(22)验算其抗震承载力是否足够。

由于钢结构延性较好，在抗震能力需求一定时，只需较低的承载力便能达到相应的设计目标。其对应的承载力抗震可靠指标较低。此时，由于地震作用的变异系数一般大于0.30[20]，远大于其他变量，因此，地震作用的统计参数对可靠指标的影响最大。为使结果具有对比性，除重力荷载统计参数稍有差异外，其余各变量的统计参数模型取与文献[9]相一致的模型，见表6。

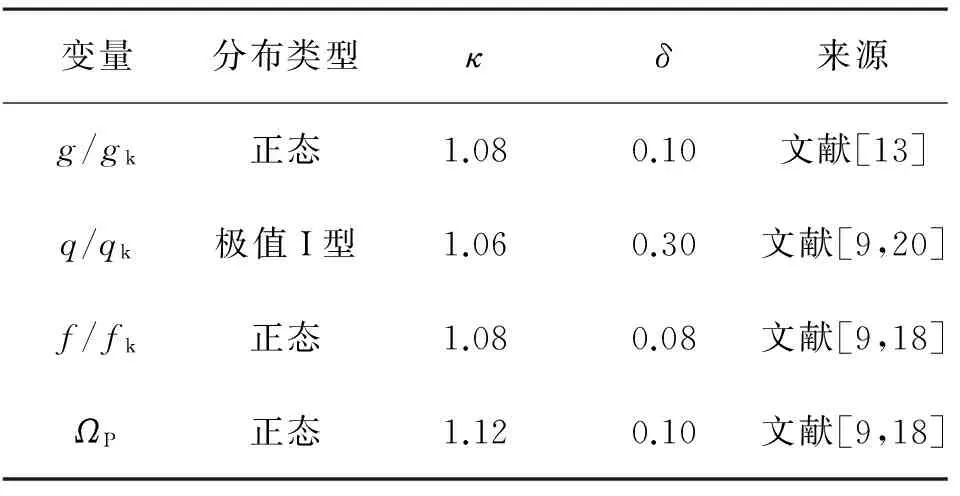
表6　钢柱可靠度分析对应的随机变量统计参数

假定某钢结构中有一偏心受压钢柱，采用工形截面524 mm×320 mm×12 mm×10 mm，Q235钢，轴压力设计值为1 100 kN，弯矩设计值为339.5 kN·m。采用Monte Carlo方法计算，同理可求得其可靠指标见表7。

表7　某钢柱设计可靠指标随ρN、ρM和η的变化

由表7可知，压弯钢柱可靠度随ρM和ρN的变化均不大，且与抗震规范模式对应的可靠度结果相差不大，说明在此情形下规范模式亦具有较好的适用性。原因主要是该钢柱失效方程中荷载相关曲线与规范考虑的情形较为一致，均为负相关。

另外，当η=1.0时，各种荷载效应比值下可靠指标平均值为1.02，与文献[9]校准分析得到的平均值1.03较为接近，这亦说明文中选取的可靠度参数分析模型较为准确。

5结论

从失效方程中荷载相关特性的角度，分析了现行柱可靠性设计方法的适用性，并得到了不同柱承载力抗震设计可靠度的变化规律。主要研究结论为：

1)水平荷载和竖向荷载组合作用下小偏压RC柱和工字型钢柱失效方程中的荷载相关曲线均近似为负相关直线，其承载力抗震可靠度随轴压力荷载效应比值变化较小，与规范模式计算值较接近。

2)水平荷载和竖向荷载组合作用下大偏压RC柱失效方程中的荷载相关曲线与现行设计规范考虑情形有较大出入，会存在明显的正相关段部分。

3)考虑失效方程中荷载正相关的特性后，大偏压RC柱承载力抗震可靠度会随轴压力荷载效应比值变化较大，与规范模式计算值有较大差异；且当轴压力荷载效应比值为负时其会低于规范模式计算值较多。

参考文献：

[1] 清华大学土木结构组,西南交通大学土木结构组,北京交通大学土木结构组. 汶川地震建筑震害分析[J]. 建筑结构学报, 2008, 29(4): 1-9.

Civil and Sructural Groups of Tsinghua University, Xinan Jiaotong University, Beijing Jiaotong University. Analysis on seismic damage of buildings in the Wenchuan earthquake [J]. Journal of Building Structure, 2008, 29(4): 1-9.(in Chinese)

[2] 叶列平,曲哲,马千里,等.从汶川地震框架结构震害谈“强柱弱梁”屈服机制的实现[J].建筑结构,2008,38(11): 52-59.

YE L P, QU Z, MA Q L, et al. Study on ensuring the strong column-weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake [J]. Building Structure, 2008, 38(11): 52-59.(in Chinese)

[3] 建筑结构可靠度设计统一标准：GB 50068-2001 [S].北京：中国建筑工业出版社，2001.

Unified standard for reliability design of building structures: GB 50068-2001 [S]. Beijing: China Architecture & Building Press, 2001.(in Chinese)

[4] GALAMBOS T V. Reliability of axially loaded columns [J]. Engineering Structures, 1983, 5(1):73-78.

[5] BRECCOLOTTI M, MATERAZZI A L. Structural reliability of eccentrically-loaded sections in RC columns made of recycled aggregate concrete [J]. Engineering Structures, 2010, 32(11):3704-3712.

[6] 蒋友宝,廖国宇,谢铭武.钢筋混凝土框架柱和轻钢拱结构失效方程复杂特性与设计可靠度[J]. 建筑结构学报, 2014, 35(4): 192-198.

JIANG Y B, LIAO G Y, XIE M W. Complex failure function and design reliability for RC frame columns and light-weight steel structures [J]. Journal of Building Structures, 2014, 35(4): 192-198. (in Chinese)

[7] 蒋友宝,廖强,冯鹏. RC偏压构件精细抗力概率模型[J].土木建筑与环境工程, 2014, 36(4):15-21.

JIANG Y B, LIAO Q, FENG P. Refined probabilistic model of resistance of RC eccentric compression member [J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(4): 15-21.(in Chinese)

[8] 建筑抗震设计规范:GB 50010-2010 [S].北京：中国建筑工业出版社，2010.

Code for seismic design of buildings: GB 50010—2010 [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)

[9] 高小旺,魏琏,韦承基.现行抗震规范可靠度水平的校准[J]. 土木工程学报, 1987, 20(2): 10-20.

GAO X W, WEI L, WEI C J. Calibration of reliability level in the curent chinese aseismic design code [J]. Journal of Civil Engineering, 1987, 20(2): 10-20.(in Chinese)

[10] FRANGOPOL D M, IDE Y, SPACONE E, et al. A new look at reliability of reinforced concrete columns [J]. Structural Safety, 1996, 18(2):123-150.

[11] HONG H P, ZHOU W. Reliability evaluation of RC columns [J]. Journal of Structural Engineering, 1999, 125(7): 784-790.

[13] 蒋友宝,杨伟军.基于偏心距随机特性的RC框架柱承载能力抗震调整系数[J].中南大学学报, 2012, 43(7): 2796-2802.

JIANG Y B, YANG W J. Seismic adjustment coefficient of bearing capacity for RC frame columns with random characteristics of eccentricity [J]. Journal of Central South University, 2012, 43(7): 2796-2802.(in Chinese)

[14] MILNER D M, SPACONE E, FRANGOPOL D M. New light on performance of short and slender reinforced concrete columns under random loads [J]. Engineering Structures, 2001, 23(1):147-157.

[15] PIRMOZ A, MAREFAT MOHAMMAD S. Reliability assessment of compression columns in seismic EBFs [J]. Journal of Constructional Steel Research, 2015, 104: 274-281.

[16] 混凝土结构设计规范:GB 50010-2010 [S].北京：中国建筑工业出版社，2010.

Code for design of concrete structures: GB 50010-2010 [S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)

[17] 钢结构设计规范：GB 50017-2003 [S].北京：中国计划出版社，2003.

Code for design of steel structures: GB 50017-2003[S]. Beijing: China Planning Press, 2003.(in Chinese)

[18] 张新培.建筑结构可靠度分析与设计[M].北京：科学出版社，2001: 1-107.

ZHANG X P. Reliability analysis and design for building structures [M].Beijing: Science Press, 2001:1-107.(in Chinese)

[19] 蒋友宝,杨毅,杨伟军.基于弯矩和轴力随机相关特性的RC偏压构件可靠度分析[J].建筑结构学报, 2011,32(8): 106-112.

JIANG Y B, YANG Y, YANG W J. Reliability analysis based on random correlative characteristics between moment and axial force for RC member subjected to eccentric compression [J].Journal of Journal of Building Structures, 2011, 32(8): 106-112.(in Chinese)

[20] 高小旺,鲍蔼斌.地震作用的概率模型及其统计参数[J]. 地震工程与工程振动, 1985, 5(1): 13-22.

GAO X W, BAO A B. Probabilistic model and its statistical parameters for seismic load [J]. Earthquake Engineering and Engineering Vibration, 1985, 5(1): 13-22.(in Chinese)

(编辑胡英奎)

Influence of correlations between loads in failure function on design reliability of seismic capacity for columns

Jiang Youbao, Sun Guoheng, Zhou Chengyu,Zhang Jianren

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004, P. R. China)

Abstract:The concrete and steel columns subjected to a combination of vertical load and horizontal earthquake action are used to study the influence of correlations between loads in failure function on design reliability of seismic capacity of columns. According to the currentCodeforDesignofConcreteStructuresandCodeforDesignofSteelStructures, the correlations between moment and axial force are analyzed for different columns. Through comparisons of different columns in several frame structures, the similarities and differences are investigated between the load interaction curves and those considered in codes. It is indicated that the load interaction curves under this combination match well with those considered in codes for RC columns with compression failure and steel columns with I-shaped section, and they are all negatively correlated straight lines approximately; the load interaction curve of RC column with tension failure is largely different from that considered in codes, and obviously has some positive correlation parts. Based the complex failure function, reliability of columns under this combination is analyzed with the Monte Carlo method and current statistics of load and resistance. The results show that: (1)the reliability indexes of seismic capacity vary lightly with different load effect ratios based on axial force for steel columns and RC columns with compression failure, and are close to those based on the codes; (2)the reliability indexes vary greatly with different load effect ratios based on axial force for RC columns with tension failure, and are also largely different from those based on the codes; (3)the reliability indexes are lower than those based on the codes for RC columns with tension failure when the load effect ratio based on axial force is negative, as a consequence, the current reliability-based design method of columns may be unsafe in this case.

Keywords:structural design; reliability; seismic capacity of column; interaction curve of loads; load effect ratio

doi:10.11835/j.issn.1674-4764.2016.03.004

收稿日期：2015-10-06

基金项目：国家重点基础研究发展计划(2015CB057705)；“湖湘青年英才”支持计划(QNYC13-2016)；“长沙理工大学青年英才”支持计划(QNYC02-2012)

作者简介：蒋友宝(1982-)，男，教授，博士，主要从事复杂结构可靠性研究，(E-mail)jiangybseu@163.com。

Foundation item：National Key Basic Research Program of China (2015CB057705); Program for Youth Talents in Hunan Province (QNYC13-2016); Program for Youth Talents in Changsha University of Science and Technology (QNYC02-2012)

中图分类号：TU312.1

文献标志码：A

文章编号：1674-4764(2016)03-0025-10

Received:2015-10-06

Author brief：Jiang Youbao(1982- ), professor, PhD, main research interest: reliability of complex structures, (E-mail) jiangybseu@163.com.