面向微博的多实体稀疏关系数据联合聚类

于淼，杨武，王巍，申国伟



面向微博的多实体稀疏关系数据联合聚类

于淼，杨武，王巍，申国伟

（哈尔滨工程大学信息安全研究中心，黑龙江哈尔滨 150001）

针对大规模微博中多实体间的稀疏关系数据，提出一种面向多实体稀疏关系数据的高效联合聚类算法。在算法中，为了充分利用多关系数据，提出了一种顽健的约束信息嵌入方法构建关系矩阵，降低了矩阵的稀疏性，进一步提高了算法的准确率。在稀疏约束的块坐标下降框架下，关系矩阵通过非负矩阵三分解算法同时获得不同实体的聚类指示矩阵。非负矩阵分解过程中，通过高效的投射算法实现快速求解，确保了聚类结果的稀疏结构。在人工和真实数据集上的实验表明，算法在3个指标上都具有明显提高，特别是在极端稀疏数据上的效果更加明显。

微博；多实体稀疏关系；联合聚类；非负矩阵分解；辅助信息嵌入

1 引言

随着互联网技术的快速发展，微博成为人们的信息分享和传播平台。为了深入理解微博平台中的用户行为、内容、传播规律等，微博已经成为社会媒体数据挖掘、社会计算等研究领域中的热点研究目标。

在微博平台中，用户可以发布或者评论一条消息，消息中可以包含标签、位置等多类特征实体。同时，用户通过关注构建用户关注关系，通过转发促进消息快速传播。微博用户通过上述行为产生大量实体及复杂的交互关系，因此，微博数据是多实体关系数据[1]。通过对微博中实体间的交互关系进行挖掘，能够深入理解微博中实体之间的潜在结构。

在挖掘多实体关系数据时，通常通过聚类算法挖掘不同实体之间的潜在结构[2,3]。聚类算法主要包括多视图聚类和联合聚类等。多视图聚类算法通常建模成星型结构[4]，而真实数据中的结构可能比星型结构要复杂很多。联合聚类算法能够同时针对2类实体进行聚类分析，并且能够快速地扩展到多阶实体关系中，因此成为目前多关系挖掘中的常用算法[1]。

在处理多关系数据时，联合聚类分析主要包括非负矩阵分解[4~7]、信息理论[8]及谱分析算法[2]。非负矩阵分解在联合聚类算法取得了很好的效果[9]，特别是在处理大规模数据时，其能够快速地扩展到分布式处理平台中。但是，数据本身的几何结构会影响非负矩阵分解结果的准确性[10,11]，特别是稀疏性结构对算法的影响较大。Hoyer针对非负矩阵分解的稀疏问题提出了稀疏约束，进而确保结果的稀疏性[12]，但该方法并没有引入到多关系数据挖掘分析中。

联合聚类算法虽然能够有效地处理多类关系数据，但是在处理真实的微博数据时仍存在以下问题：由于用户隐私保护、微博平台API限制等因素，抽取的实体及实体关系并不完备，因此构建的实体间关系非常稀疏。另外，在针对某些实体进行关系挖掘时，仅仅考虑关系中2类实体间的交互关系，显然遗漏了大量的信息。

针对上述不足，本文提出了面向多实体稀疏关系数据的联合聚类框架。框架从用户和消息2类最重要的实体出发，通过稀疏联合聚类算法对用户和消息同时挖掘分析。为了进一步降低矩阵的稀疏度，充分利用实体内部的交互关系及与其他实体间的交互关系进一步提高算法的准确率，提出了基于距离学习的辅助信息嵌入方法将用户和消息对应的同质关系以及消息包含的特征向量融合到用户和消息间的关系矩阵中，进一步提高了稀疏联合聚类算法的准确率。

2 问题定义

微博中包含大量的实体，且同类实体间、不同类实体间存在大量的交互关系。抽取微博中的实体及交互关系如图1所示。

通过对微博中多实体交互关系的分析可知，用户和消息是微博中最重要的2类实体。同时，消息中包含大量的特征实体、特征实体集合。用户和消息之间的交互关系可以构建关系矩阵，用户之间的关注关系通过矩阵表示，消息之间的转发关系通过矩阵表示，消息中包含多类特征实体采用特征向量表示。

微博中用户和消息间的关系挖掘转换成基于用户和消息间关系矩阵的联合聚类分析。挖掘用户和消息的潜在关系，为主题社区、微博位置推理等提供基础。

3 多实体稀疏关系联合聚类框架

针对微博中多实体的关系挖掘，本文提出了多实体稀疏关系联合聚类框架，如图2所示。在该框架中，主要包括3个核心步骤，分别是关系抽取及建模、辅助关系数据嵌入、稀疏约束下的关系矩阵三分解。

针对微博数据，抽取实体及实体关系。在此基础上，构建关系矩阵表示实体间的交互关系。由于微博中实体较多，文中以用户和消息2类最重要的实体为基础，可得到用户和消息的关系矩阵，用户、消息对应的内部关系矩阵、，以及消息包含的特征属性向量。由于微博中用户间的交互很难抽取完整的交互关系，因此，用户与消息间的关系矩阵并不考虑交互频次，其计算公式如下

为了进一步降低关系矩阵的稀疏度，充分利用用户和消息2类实体对应的矩阵和以及消息对应的特征属性向量。

在真实的微博数据中，即使融合了用户和消息对应的关系矩阵、及特征属性，用户和消息间的关系矩阵仍然非常稀疏，因此，采用基于稀疏矩阵三分解的联合聚类同时得到用户和消息的聚类关系，进一步挖掘出用户和消息的潜在关系。

4 多实体稀疏关系联合聚类算法

多实体稀疏关系联合聚类算法首先通过距离度量学习嵌入辅助信息，进一步通过非负矩阵三分解实现稀疏关系矩阵分解。

4.1 基于距离学习的辅助关系嵌入

通过对微博数据中的关系进行分析可知，用户和消息之间的异质关系非常稀疏。为了提高联合聚类算法的效果，在用户和消息之间的关系矩阵基础上，通过距离度量学习[13]将用户间和消息对应的关系矩阵、嵌入到异质关系矩阵中。

在聚类的过程中基于距离度量学习的方法融合相似性和相异性约束关系矩阵是一种基本信息嵌入方法[13]。本文中同时考虑用户和消息2类实体的同质关系，将分别学习2个距离度量、。为了得到2个距离度量，首先给出基于用户和消息的关系矩阵、对应的相似性和相异性约束关系矩阵。

基于用户共同关注用户构建的用户相似性和相异性矩阵计算为

(3)

基于消息传播路径用户和消息特征属性构建的消息相似性和相异性矩阵计算为

(5)

为了叙述方便，以用户同质性关系嵌入为例进行说明。对于异构关系矩阵中任意给定的两行和，可以定义其马氏距离

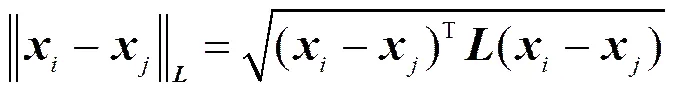
文献[13]直接学习距离度量，但是直接学习的方法很难处理孤立点，而实际的数据中经常包含大量的孤立点。因此，本文将采用新的学习算法，提高距离度量的顽健性[14]。

由于距离度量是正半定矩阵，因此可以对进行特征值分解，即满足。马氏距离度量可以改写成

(8)

(10)

与用户同质关系距离度量求解方法类似，消息同质性关系距离度量对应的目标函数为

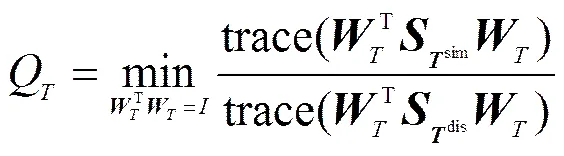
关系矩阵可通过用户和消息2个距离度量嵌入对应的同质性关系，形成新的异质关系矩阵。

4.2 基于非负矩阵三分解的稀疏联合聚类算法

因此，对于新的行、列的关系矩阵，在稀疏约束下，非负矩阵三分解对应的目标函数为。

(14)

Kim等[16]将非负矩阵分解方法都归纳到块坐标下降的框架下进行求解，并且具有较快的收敛速度。针对目标函数，对列向量块进行稀疏约束。可以看成是个列向量，每一个列可以看成是一个块，因此可以采用块坐标下降的方法进行求解。

(16)

式（16）可以采用列的形式表示，因此可以通过如式（16）进行求解

在上述分析的基础上，下面将给出本文的处理算法。在非负矩阵三分解基础上，融合辅助信息嵌入，实现多实体稀疏关系联合聚类，整体算法如算法1所示。式（17）可以分解成算法1中步骤4）和步骤5）分别进行求解。每一次迭代，对每一列进行透射处理。稀疏约束下投射函数project()的求解方法很多。Thom等[17]提出了一种高效的稀疏确保的投射算法，本文将采用其算法进行求解。由于篇幅限制，本文将省略投射函数的介绍。在步骤14）中，采用乘法更新的方法迭代求解矩阵。在步骤15）中，采用最小二乘法求解矩阵。在多次迭代之后达到收敛时算法结束，输出指示矩阵、。

算法1 基于非负矩阵三分解多实体稀疏关系矩阵联合聚类算法SNMTF

输入 关系矩阵、、及特征向量，稀疏度，聚类数目

输出 用户、消息聚类指示矩阵、

1) 初始化矩阵、、、、

7) repeat //迭代求解、、

8) for=1 todo //按列投射求解

13) end for

16) 收敛结束循环

17) 输出聚类指示矩、

5 实验及分析

本文所有实验都在Matlab下实现，硬件平台为Intel Core I5-3470、3.2 GHz、6 GB内存，Linux和Matlab 2011a，可视化工具为NodeXL。

实验中将分别对比算法ITCC[8]、SSNMF[18]、FNMTF[7]和本文算法SNMTF。每一组实验分别运行10次，实验结果中给出平均值。

5.1 评估指标

联合聚类算法的度量指标较多，本文将采用常见的Purity[19]、NMI[20]、ARI[21]这3个指标作为度量标准。对于给定的异构数据集，实体规模为，算法得到的聚类结果为，给定的聚类标签为，则3个评估指标分别定义为

(19)

(20)

5.2 人工数据集实验

本文首先在联合聚类算法的标准测试数据集[22]上对算法进行全面评估。该数据集给出了2类实体的聚类标签，不仅能够针对算法的准确率等指标值进行对比分析，还能对算法在不同聚类难度等级的数据集下进行对比分析。

数据集中共有36组数据，通过贝叶斯错误率作为数据集的难度控制参数，包括5%、12%、20%这3个难度等级，其中，5%是最容易聚类的数据集，20%是最难聚类的数据集。每一个难度等级分别对应50、100、200、500这4种规模（行和列的规模相同），可针对节点规模进行聚类算法对比分析。每一类节点规模的数据集分别对应3、5、10这3种聚类数目，可针对不同的聚类数进行对比分析。

在同一规模的数据集下评估算法受不同聚类数目的影响情况，对比结果如图3所示。所有的算法都随着值的增加，准确率都有所下降，但其他2个指标影响较小。

图4为在不同数据规模下的对比结果。随着规模的增加，算法的准确率等指标都随之下降。由于该数据集中的测试数据并没有特别稀疏的情况，因此无法发挥算法SNMTF的优势，其聚类结果接近于FNMTF算法。

针对标准测试数据集中不同聚类难度等级的数据集进行算法的顽健性对比实验，结果如图5所示。本文算法在处理不同聚类难度等级的数据集时的顽健性都优于其他3种算法。

5.3 真实数据集实验

为了验证SNMTF算法在真实数据集上的效果，通过微博API收集了Weibo数据集。该数据集收集了2012年“闯红灯”、“丰田汽车回收”、“美国总统大选”、“莫言获得诺贝尔奖”、“我是特种兵”、“杭州烟花大会”、“中国好声音”7个话题的新浪微博消息。通过API进一步收集消息发布用户的属性信息。通过预处理得到5 403个用户的8 023条微博、374个标签、984条位置信息及14 500个描述词。根据上述实体对应的关系数据构建对应的关系矩阵。

5.3.1 对比实验及分析

为了验证算法在真实微博数据集中的聚类结果，本文以微博消息为观察对象。4个算法的实验结果如表1所示。由结果可知，本文算法SNMTF比其他3种算法的效果都要好。这主要得益于本文采用的是稀疏关系矩阵分解实现联合聚类，确保了聚类结果的稀疏结构。算法中通过距离度量学习嵌入了特征属性等辅助信息，进一步提高了算法的准确率。

表1 算法在微博数据集中的对比结果(K=7)

4个算法在微博数据集上的运行时间对比结果如图6所示。由图中结果可知，本文算法SNMTF只比目前最快的FNMTF算法的运行时间稍微多一点，这主要是由于在算法SNMTF中加入了辅助信息嵌入过程。算法SSNMF采用乘法更新的迭代求解方法实现非负矩阵分解，因此其运行时间最长。

本文提出的算法SNMTF需要用户提供稀疏约束参数。为了评估稀疏参数对实验结果的影响，本文通过改变稀疏约束参数，得到算法在不同指标下的结果如图7所示。由图7中结果可知，在0.08到0.2之间算法对稀疏参数的影响较小，因此，在对比实验及后续的实验中设置稀疏约束参数为0.1。

5.3.2 实例分析

为了分析算法的真实应用价值，本文针对微博数据集中的“中国好声音，梁博冠军”的话题进行详细分析。在该话题形成过程中，用户发布大量的微博消息。通过本文算法对微博数据集进行聚类分析得到的可视化结果，图8中给出了Top 10用户、Top 5位置、Top 5描述词。

通过图中的Top用户可以分析该话题形成过程中影响力较大的用户，并且可以分析话题主题词及对应的位置属性信息，为微博数据挖掘分析提供了基础。

5.3.3 位置预测应用

为了说明本文算法在微博用户发布消息时的位置预测应用中的效果，在实验中选择了500条带有位置的消息作为测试数据集。由于位置标记不是很规范，因此，以行政市作为位置标签。将测试数据集的消息按照50%、60%、70%、80%、90%的比例融合到原始数据集中。

微博用户预测中最常应用的有2种方法：一种是基于用户属性的位置预测，记为Profile-based方法[23]；一种是基于用户好友关系的位置预测，记为Group-based的方法[24]。本文选择这2种方法作为对比方法，实验结果如图9所示。

通过图9的结果分析可知，本文提出的基于辅助信息嵌入的联合聚类算法的效果最佳，并且随着训练数据规模的增加，准确率也越高。这主要得益于本文算法确保了聚类结果的稀疏结构，并且嵌入了其他辅助信息。Profile-based方法的准确率最低，这是由于微博用户中大量的消息并没有给出位置信息，并且用户在现实世界中是动态调整的，因此，用户属性可能成为历史属性。Group-based方法的用户位置预测准确率较高，但是并没有将用户关系区别对待，降低了预测的准确率。

6 结束语

本文针对微博数据中的多实体稀疏关系数据提出了一种多实体稀疏关系联合聚类算法SNMTF。算法在块坐标下降框架下，采用稀疏约束的块向量投射算法实现快速的非负矩阵三分解。为了进一步降低关系矩阵的稀疏度，采用了基于距离学习的辅助关系数据嵌入，进一步提高了算法的准确率。实验结果表明本文提出的算法在标准测试数据集和真实微博数据集中的效果都优于现有的算法。

本文只考虑了消息特征属性的嵌入，下一步将同时考虑用户和消息的属性信息，进一步提高算法的聚类准确率。另外，将本文算法扩展到分布式平台中处理大规模数目。

[1] GAO D, ZHANG R, LI W, et al. Twitter hyperlink recommendation with user-tweet-hyperlink three-way clustering[C]//The 21st ACM International Conference on Information and Knowledge Management. ACM, c2012: 2535-2538.

[2] LONG B, ZHANG Z, W X, et al. Spectral clustering for multi-type relational data[C]//The 23rd International Conference on Machine Learning. Pittsburgh, Pennsylvania, ACM, c2006: 585-592.

[3] WANG H, HUANG H, DING C. Simultaneous clustering of multi-type relational data via symmetric nonnegative matrix tri-factorization[C]//The 20th ACM international Conference on Information and Knowledge Management. Glasgow. Scotland, UK, ACM, c2011: 279-284.

[4] LIU J, WANG C, GAO J, et al. Multi-view custering via joint nonnegative matrix factorization[C]//2013 SIAM International Conference on Data Mining. SIAM. c2013.

[5] WANG H, HUANG H, DING C. Simultaneous clustering of multi-type relational data via symmetric nonnegative matrix tri-factorization[C]// The 20th ACM International Conference on Information and Knowledge Management. ACM, C2011: 279-284.

[6] LIU Y, SHEN C. Orthogonal nonnegative matrix factorization for multi-type relational clustering[J]. International Journal of Computer and Information Technolog, 2013, 2(2): 215-221.

[7] WANG H, NIE F, HUANG H, et al. Fast nonnegative matrix tri- factorization for large-scale data co-clustering[C]//The 22nd International joint Conference on Artificial Intelligence, China, c2011: 1553-1558.

[8] DHILLON I S, MALLELA S, MODHA D S. Information theoretic co-clustering[C]//The 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, c2003: 89-98.

[9] LI T, DING C. The relationships among various nonnegative matrix factorization methods for clustering[C]//The 6th International Conference on Data Mining. Hong Kong, China, c2006: 362-371.

[10] GU Q, ZHOU J. Co-clustering on manifolds[C]//The 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, c2009: 359-368.

[11] LI P, BU J, CHEN C, et al. Relational co-clustering via manifold ensemble learning[C]//The 21st ACM International Conference on Information and Knowledge Management. ACM, c2012: 1687-1691.

[12] HOYER P O. Non-negative matrix factorization with sparseness constraints[J]. The Journal of Machine Learning Research, 2004, (5): 1457-1469.

[13] XING E P, JORDAN M I, RUSSELL S, et alDistance metric learning with application to clustering with side-information[C]//Advances in Neural Information Processing Systems. c2002: 505-512.

[14] WANG H, NIE F, HUANG H. Robust distance metric learning via simultaneous l1-norm minimization and maximization[C]//The 31st International Conference on Machine Learning. c2014: 1836-1844.

[15] HSIEH C-J, DHILLON I S. Fast coordinate descent methods with variable selection for non-negative matrix factorization[C]//The 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, c2011: 1064-1072.

[16] KIM J, HE Y, PARK H. Algorithms for nonnegative matrix and tensor factorizations: a unified view based on block coordinate descent framework[J]. Journal of Global Optimization, 2013, 58(2): 285-319.

[17] THOM M, PALM G. Efficient sparseness-enforcing projections[J]. arXiv preprint arXiv:13035259, 2013.

[18] CHEN Y H, WANG L J, DONG M. Non-negative matrix factorization for semisupervised heterogeneous data coclustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1459-1474.

[19] ZHAO Y, KARYPIS G. Criterion Functions for Document Clustering: Experiments and analysis[R]. City, 2001.

[20] STREHL A, GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. The Journal of Machine Learning Research, 2003, 3: 583-617.

[21] HUBERT L, ARABIE P. Comparing partitions[J]. Journal of Classification, 1985, 2(1): 193-218.

[22] LOMET A, GOVAERT G, GRANDVALET Y. Design of Artificial Data Tables for Co-clustering Analysis[R]. City, 2012.

[23] MCGEE J, CAVERLEE J, CHENG Z. Location prediction in social media based on tie strength[C]//The 22nd ACM international Conference on Information and Knowledge Management. San Francisco, California, USA, ACM. c2013: 459-468.

[24] LI R, WANG S, DENG H, et alTowards social user profiling: unified and discriminative influence model for inferring home locations[C]//The 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China, ACM, c2012: 1023-1031.

Co-clustering of multi-entities sparse relational data in microblogging

YU Miao, YANG Wu, WANG Wei, SHEN Guo-wei

(Information Security Research Center, Harbin Engineering University, Harbin 150001, China)

For large-scale sparse relation data of multi-entity in microblogging, an efficient co-clustering algorithm was proposed which processed sparse relation data of multi-entity. In order to take full advantage of multi-relational data when using this algorithm, a robust constraint information embedding algorithm was proposed to construct relation matrix, and the performance of relation mining was improved by reducing matrix sparsity. In the sparse constraint block coordinate descent framework, relation matrix concurrently obtained cluster indication matrix of different entities by non-negative matrix tri-factorization. In non-negative matrix factorization, to ensure sparse structure of clustering result, a quick solution was achieved through efficient projection algorithm. Experiments on synthetic and real data sets show that proposed algorithm goes beyond all the baselines on three indicators. The improvement is more significant especially when processing extremely sparse data.

microblogging, multi-entity sparse relation, co-clustering, non-negative matrix factorization, auxiliary information embedding

TP393

A

10.11959/j.issn.1000-436x.2016019

2015-04-05；

2015-10-20

杨武，yangwu@hrbeu.edu.cn

国家高技术研究发展计划（“863”计划）基金资助项目（No.2012AA012802）；国家自然科学基金资助项目（No.61170242）

The National High Technology Research and Development Program of China (863 Program) (No.2012AA012802), The National Natural Science Foundation of China (No.61170242)

于淼（1987-），男，黑龙江牡丹江人，哈尔滨工程大学博士生，主要研究方向为数据挖掘、社会计算。

杨武（1974-），男，辽宁宽甸人，博士，哈尔滨工程大学教授、博士生导师，主要研究方向为信息安全、数据挖掘、互联网安全。

王巍（1974-），男，黑龙江哈尔滨人，博士，哈尔滨工程大学副教授，主要研究方向为数据挖掘、网络安全。

申国伟（1986-），男，湖南邵阳人，哈尔滨工程大学博士生，主要研究方向为数据挖掘、信息安全。