多重分形在沪深300股指期货市场的应用研究

◇陈仁莲



多重分形在沪深300股指期货市场的应用研究

◇陈仁莲

摘要：本文采用Hurst指数检验法，分析沪深300股指期货市场是否存在多重分形特征。运用MF-DFA法，结合mat鄄lab，做出沪深300股指期货收益率序列的多重分形谱f（α）与奇异指数α的关系图，知收益率序列的标度指数也将不同，进而通过多重分形参数△α来初步预测股指期货合约价格走势。

关键词：多重分形；多重分形谱；市场风险测度指标；投资分析

10.13999/j.cnki.scyj.2016.06.023

金融市场的研究一直是大家关注的热点，而分形理论的出现，给金融市场的探索开辟了另一条道路。1964年Mandelbrot[1]在研究资本市场的收益率时就有了分形思想，Peters （1994）[2]提出金融市场分形理论。随着分形市场理论的研究不断深入，对证券市场的研究结果表明：大多数市场具有明显的分形特征：自相似性、显著的 Hurst指数以及平均循环长度[3-5]；许涤龙（2004）、黄诒蓉（2005）等分别利用 R/S分析方法得到我国股市的 Hurst指数和平均统计循环长度，以不同形式的结果表明，我国金融市场存在长期自相关性[6-7]。然而以上研究均仅考虑金融时间序列的单分形过程，事实上，不同证券市场的价格变化或收益率变化具有多重分形特征[8-11]。本文主要运用多重去趋势波动分析（MF-DFA）及多重分形谱来研究沪深300股指期货收益率。为投资者认知我国市场提供帮助，运用分形特征获取最大利益。

一、数据描述

沪深300股指期货是以沪深300指数作为标的物的期货品种，在2010年4月由中国金融期货交易所推出。本文选用的样本数据为2010年4月26日至2016年3月27日的沪深300股指期货（IF8888）收盘价格数据，来源于同花顺期货行情系统。首先对数据进行分析和预处理，剔除不完整数据，共余1443个有效数据。先选用大家熟悉的对数收益率为研究对象，即：

其中Rt（τ）表示在时间标度τ下t时刻的收益率，τ=1、5、22（对应为日、周、月），P（t）为t时刻价格。

二、数据处理

本文主要采用多重分形方面的方法并结合matlab软件处理所获得数据。

消除趋势波动分析方法（DFA）是由Peng[12]（1994）等在研究DNA机理时采用的标度指数计算方法，用于分析时间序列的长程相关性。但DFA算法只适合分析一维的单重分形时间序列。Kantelhardt[13]（2002）等将多重分形运用到DFA方法，提出用多重分形趋势波动分析方法（MF-DFA）来刻画时间序列在不同时间标度下的多重分形特征，其步骤如下：

考察时间序列{X（t）}（t=1，2，…，N）的q阶配分函数Xq（s）：

MF-DFA法与DFA法的前三步相同。

第四步:对所有子区间取平均,即得q阶波动函数：

第五步：对同一q,描绘Xq（s）对s的双对数曲线。

Xq（s）是q和s的函数。对于同一q，Xq（s）随s的增大而增大。Xq（s）也随着多项式的阶数 m的变化而变化，s的变化范围为s≥m+1。

如果时间序列X（t）具有标度特性,则Xq（s）与s成幂律关系：

Xq（s）与s的双对数曲线应存在线性关系：

其中h（q）称为广义赫斯特指数（Hurst）。当h（q）为q的函数时，序列X（t）具有多重分形特性；当h（q）=0.5时，序列{X （t）}不相关。

1.Hurst指数检验

用Hurst指数检验沪深300股指期货是否具有多重分形结构，不妨取q为-10到10之间的整数，运用MF-DFA并结合matlab软件得广义Hurst指数，见图1。

图1　q-Hurst指数图

由图1知，Hurst指数h（q）随着q的不同而不同。当取t= 1、5、22时，三条Hurst指数曲线h（q）都随着q的增大而减小，因此不同时间标度下的沪深300期货市场存在多重分形特征。同时，q=0的右边附近像是一个拐点，h（q）>0.5，从而说明市场存在长期记忆性，而当h（q）<0.5，说明市场存在反持续性。

2.多重分形谱（MFS）分析

多重分形描述的是分形几何体在生长过程中不同层次的特征。定义α为不同小区域内的生长几率，令有相同α值的小区域构成一个子集，则α称为局部分维，或奇异指数。f（α）表示相同α值的子集的分形维，如果把不同的α值下对应的f （α）放在一起，这时的f（α）称为多重分形谱。而多重分形谱曲线是f（α）随α变化的曲线，若能够找到f（α）与α关系，便可以获得某一时间序列下的多重分形谱。故对（5）进行Legendre变换:

对沪深300股指期货τ=1（日）的收益率结合matlab软件作MF-DFA分析，s为天，q取-10到10之间的整数，结果如图2。

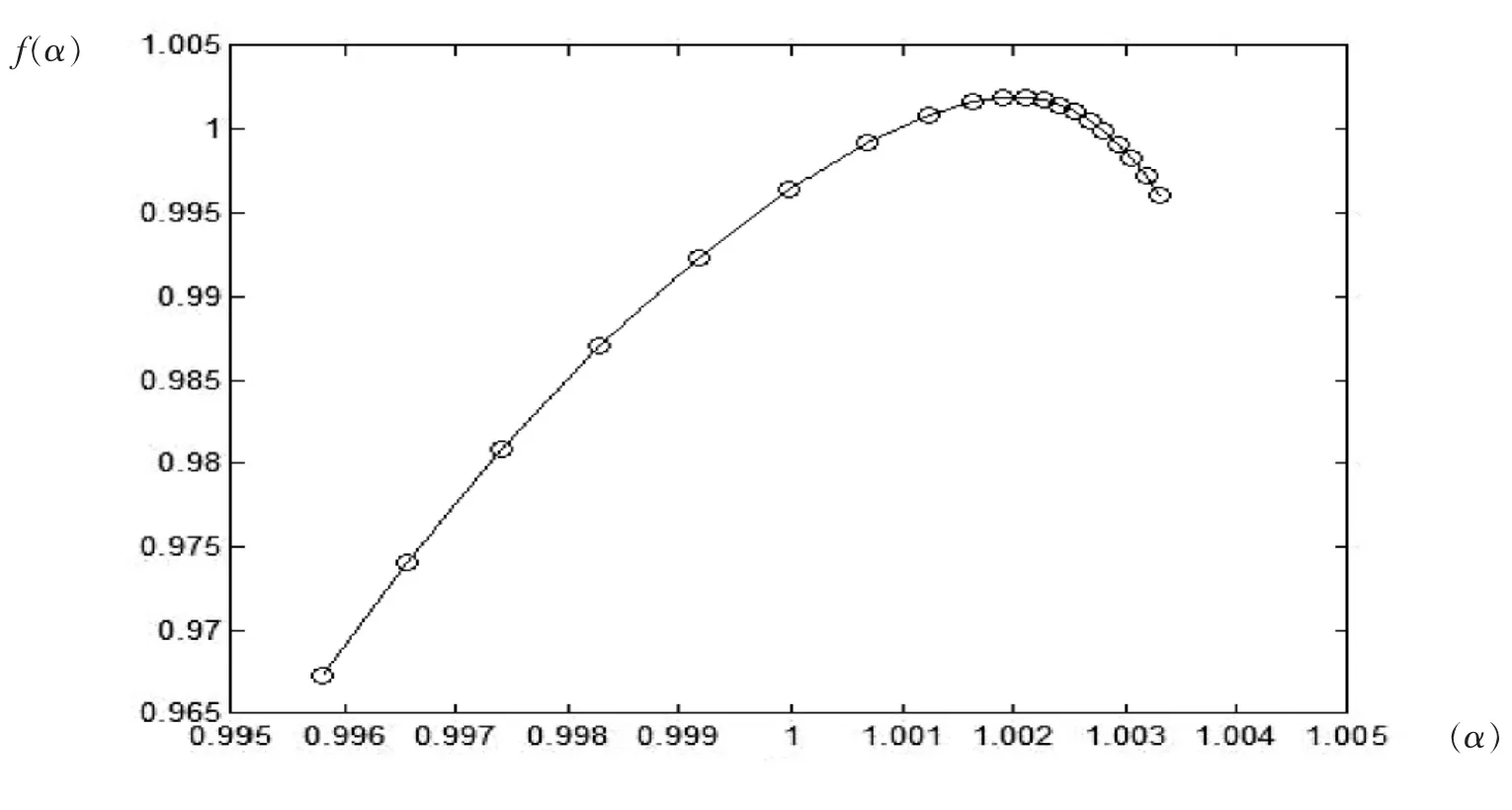
图2　τ=1时收益率Rt（τ）的MF-DFA分析

图2是沪深300股指期货序列的多重分形谱，可以看出：第一，分形谱是不对称的，呈现右偏状。τ=1时，α∈（0.9962，1.0033），说明α在不断的变化。第二，α范围随着时间标度的增加逐渐增大，f（α）的取值变化为（0.9672，1.0019），且当约q=0时取得最大值，因此f（α）是一条光滑的曲线，所以收益率序列的标度指数也将不同。

由于分形谱的宽度△α=αmax-αmin，运用matlab做出股指期货合约走势图3和△α的趋势图4，如下：

图3　股指期货合约走势图

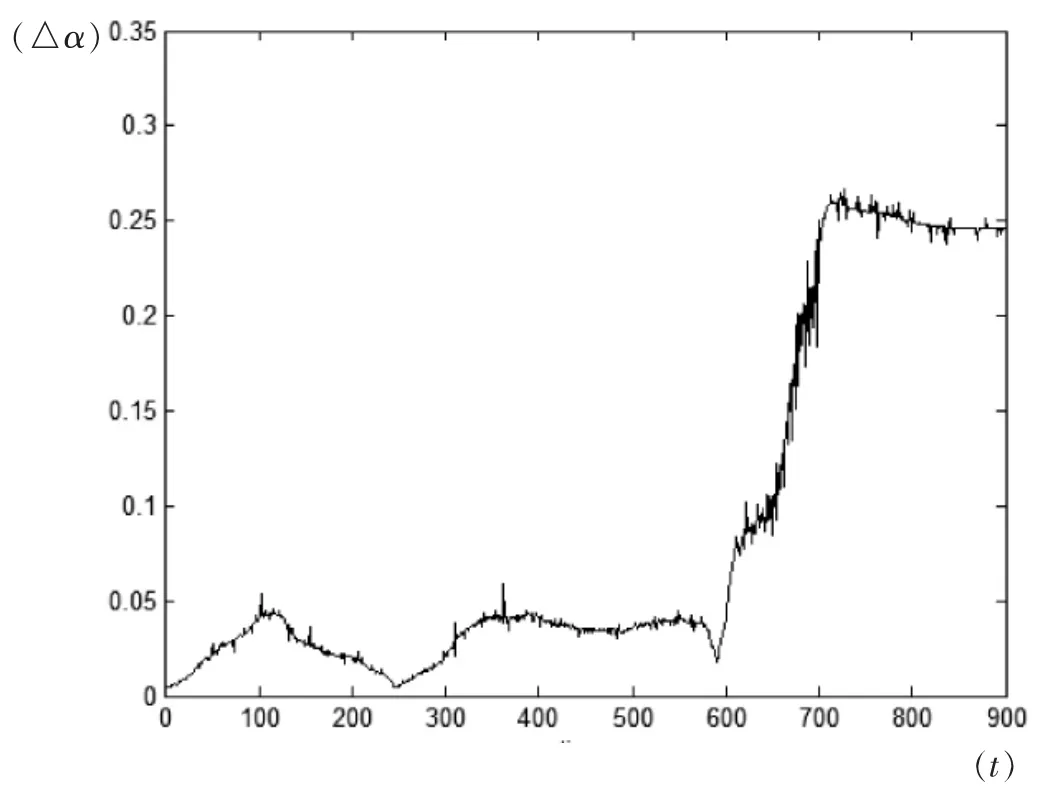
图4　△α的趋势图

图3为沪深300股指期货合约走势,图4是根据移动窗口求出的沪深300股指期货合约的多重分形参数△α的走势。对比可知，多重分形谱参数△α与沪深300股指期货合约价格走势大体上吻合，说明两者之间有一定的相关性。因此可以粗略地用△α来预测股指期货合约价格的变化趋势。

三、结论

综上对沪深300股指期货合约走势的Hurst指数分析，知其市场存在多重分形特征。运用MF-DFA法，结合matlab软件，观察出沪深300股指期货收益率序列的 f（α）与 α的关系图，可知收益率序列的标度指数也将不同，进而通过多重分形参数△α来初步预测股指期货合约价格走势，因此具有一定的指导意义和价值。

参考文献：

[1]B Mandelbrot.The variation of certain speculative prices[J]. Journal of business,1963（36）.

[2]EE Peters．Fractal market analysis：applying chaos theory to in鄄vestment and economics[M].New York:John Wiley＆Son Lnc.,1994.

[3]SR Hurst,E Platen,ST Rachev.Option pricing for a log sta鄄ble asset price model[J].Mathematical and Computer Modelling, 1999（29）.

[4]MKP So.Long-term memory in stock market volatility.Ap鄄plied Financial Economics,2000（10）.

[5]T.Henry.Long memory in stock returns:some international evidence[J].Applied Financial Economics,2002（12）.

[6]邹新月,许涤龙.H指数估计方法的有效性检验[J],统计研究, 2004（08）.

[7]黄诒蓉.中国股市分形结构的 R/S实证分析[J],现代管理科学,2005（02）.

[8]Sun X,Chen H P,et al.Multifractal analysis of Hang Seng in鄄dex in Hong Kong stock market[J].Physica A,2001（09）.

[9]Lu Fangyuan.The multifractal analysis on stock market returns in China[J].Systems Engineering-Theory&Practice,2004 （06）.

[10]郝冰,陈付彬,禹旺勋.多重分形谱主要系数在股票预测问题中的研究[J].价值工程,2016（03）.

[11]张羽.中国股市分形特征及其应用研究[D].合肥：安徽大学, 2014.

[12]CK Peng,SV Buldyrev,et al.Mosaic organization of DNA nucleotides[J].Physical Review E,1994（02）.

[13]JW Kantelhardt,SA Zschiegner,et al.Multifractal detrended fluctuation analysis of nonstationary time series[J].Physica A,2002 （16）.

基金项目：茂名市软科学项目（20140340）。

作者单位：（广东石油化工学院理学院）