应用FP树快速生成无关集算法

许普乐，纪　允，张　勤

(1.芜湖职业技术学院 教务处，安徽 芜湖 241006；2. 中国移动通信集团安徽有限公司 铜陵分公司，安徽 铜陵 244000；3. 安徽林业职业技术学院 信息与艺术系，安徽 合肥 230031)



应用FP树快速生成无关集算法

许普乐1，纪允2，张勤3

(1.芜湖职业技术学院 教务处，安徽 芜湖 241006；2. 中国移动通信集团安徽有限公司 铜陵分公司，安徽 铜陵 244000；3. 安徽林业职业技术学院 信息与艺术系，安徽 合肥 230031)

摘要：δ无关集的引入可解决数据挖掘领域中挖掘出来的频繁项集数量过大以及在实际应用中获取准确项集支持度代价过大的问题。针对传统方法生成无关集生成效率过低等问题，本文提出了一种在FP树上快速生成、结合一定的剪枝策略的快速挖掘算法FMINEX。实验效果证明，该算法在挖掘过程中，时间和空间性能都比较好。

关键词：数据挖掘；频繁项集；δ无关集；FP树；剪枝策略

DOI：10.13757/j.cnki.cn34-1150/n.2016.02.015

对一个数据库而言，一个重要的数据挖掘目标就是频繁项集的抽取。而抽取出来的频繁项集主要用处就是提供一个项集的支持度。这在很多应用领域非常重要，例如在关联规则的使用过程中，必须知道规则的支持度，才能计算规则的置信度。然而，在实际使用的过程中，抽取出来的频繁项集数量非常庞大，需要耗费大量的存储空间。同时在使用之前必须进行检索才能得到一个任意项集的支持度，非常耗时，增加了CPU的代价[1-2]。

在实际使用过程中，很多数据挖掘问题，例如关联规则[3-5]，就是查询一个模式或者项集的出现频率，这其实是频繁项集频繁度查询问题。一个重要但很困难的问题是，频繁项集的组合呈爆炸式增长，这样对于海量的频繁项集的支持度查询计算变得很不切实际。在实际过程中，对于一个频繁项集的支持度查询，其实只需知道其大致支持度即可，即一个项集的支持度是用其真正的支持度在一定允许范围内的变动结果代替。文献[6]提出使用大致近似支持度查询结果概念，称之为ε适当表示。适当表示模型[6]是一些数据表现模式，可以替代原有精确的查询模型，但是最终会损失一些精度，损失的精度以ε表示。

将这种ε适当表示引入到频繁项集领域中，转化成一种频繁项集的有损精简表示模型，称之为δ无关集[7]，例如在数据库D中，项集ABC的支持度为998，项集AB的支持度为1 000，那么规则AB⟹C几乎在数据库D中是正确的。因为规则除了两个例外，AB出现的交易记录中几乎都出现了C。那么规则AB⟹C的支持度其实近似和项集AB的支持度是相等的，则项集ABC的支持度可以近似地由项集AB代替。项集ABC是冗余的，因为规则AB⟹C是成立的，除了很少的部分外。

一个项集X是无关的，X中的项不能构成一个近似精确规则。文献[7]挖掘δ无关集使用的是广度优先策略，这样的策略导致δ无关集的生成效率并不高。因此，本文提出基于FP树上快速挖掘δ无关集中元素的算法FMINEX，该算法使用FP树结构代替传统的数据库，并且结合一定的剪枝策略，从而实现快速生成。

1相关概念

定义1数据库D，R集合是项的集合，一条记录r是R的子集，数据库是多条r的组合。

定义2支持度，项集X的支持度是在数据库D中出现X的交易记录个数，记为Freq(X)。

定义3频繁项集，项集X的支持度大于最小支持度σ，则成为频繁项集，记为Freq(X，σ)。

定义4关联规则，设R是所有项的集合，基于R的关联规则的表现形式是X⟹Y，其中X，Y属于R，Y≠Ø，X∩Y=Ø。

定义5δ强规则，一个δ强规则是在数据库D中，关联规则X⟹Y，其中Freq(X)-Freq(X∪Y)<=δ。说明X和X∪Y的支持度不相差δ行。

定义6δ无关集， 设项集X为δ无关集，当且仅当基于项集X没有δ强规则，则记为Free(X，δ)。

定义7频繁无关集， 如果δ无关集是频繁的，大于等于最小支持度σ，则δ无关集是频繁无关集，记为FreqFree(X，σ，δ)。

定义8频繁无关集的负边界， 无关集的负向边界记为Bd-(r,σ,δ)={X|X⊆R,X∉FreqFree(X，σ，δ)∧

[∀Y⊂X,Y∈FreqFree(r，σ，δ)]}如果项集是频繁的，则为频繁无关集的负向边界，记为FreeBd-(r,σ,δ)。

2无关集精简表示模型和FP树

2.1无关集精简表示模型

无关集精简表示模型主要有两部分组成，δ无关集和其对应的支持度FreqFree(r，σ，δ)，以及频繁无关集负边界FreeBd-(r,σ,δ)所组成。

设项集X，如果∃Y∈FreeBd-(r,σ,δ),Y⊆X，则Freq(X)=0，否则Freq(X)=min{Y|Y⊆X,Y∈FreqFree(r，σ，δ)}。

在文献[7]中，BoulicautJF等人提出算法MINEX挖掘无关集所需要的元素，δ无关集以及频繁负向边界，其主要算法如下：

FreqFreei;={X|X∈Ci,andXisaσfrequentδfreesetindatabase}

Ci+1:={X|X⊆Rand∀Y⊂X,Y∈Yj≤iFreqFreej}Yj≤iCj

i:=i+1

从这里可以看出，算法MINEX的过程主要采用类似于Apriori算法的广度优先策略，为了得到每个候选项集的支持度需要扫描数据库一次，同时对于每个候选项集存在重复生成的问题。这两个缺点导致了该算法的生成效率不高。

无关集也有类似于Apriori性质[8-11]，即无关集的所有直接子集都是无关的，非无关集的超集都非无关集。但是判断X是否是无关集，需要遍历X的直接子集。如果X不是无关集，则存在一个项集A∈X，Y=XA，如果Y不是无关集，或者Y是无关集并且Y⟹A是一个δ强规则。简而言之，就是在第i次迭代过程中，首先计算δ强规则X⟹{A}，其中X是无关集，A∈RX，其中R是全部项。这样就可以利用X∪A删除i+1次生成的候选项集中不是δ无关集。

2.2FP树

FP树[12]主要为了快速生成频繁项集。在实际数据库中有很多交易记录是相同的，反复扫描会增加I/O代价。FP树的主要思想就是将数据库中的交易记录压缩成一棵树，将交易记录尽可能的压缩在一起，从而减少搜索时间。同时在生成的过程中使用剪枝策略，进一步加快生成速度。生成的FP树有足够的信息生成所有的频繁项集。

FP树的生成主要分为两步：先扫描数据库，得到所有项的出现次数，并且进行降序排序；然后将数据库中的每条记录严格按照降序的次序进行排序，同时将其插入到FP树中，最终生成FP树。在交易记录排序和插入过程中，如果某一项的支持度小于最小支持度，则将其删除。

FP树的主要组成为FP树上的节点和头表节点。树上的节点主要由项和项在该处出现的次数组成。头表节点只要包括项和项在数据库中出现的次数以及指向树中第一个项的节点。

3FMINEX算法

针对无关集需要反复扫描数据库和存储重复生成的两个问题，FMINEX算法提出在FP树上解决。该算法主要在FP树上反复迭代的过程中得到项集，对于每一个项集进行判断，同时在生成新的FP树的时候根据无关集的反单调性质对FP树进行剪枝，使得生成的新FP树更小。

3.1理论基础

由数据库生成的FP树，可以有完整的信息生成所有的频繁项集。因为频繁项集具有反单调性质，所以如果一个项集不是频繁的，则其超集必定不是频繁的。在FP树中的表现就是如果一个项集不是频繁的，则不需生成其条件数据库。FP树是不断的迭代生成频繁项集的条件数据库，从而挖掘出所有的频繁项集。

在FP树上，也可以使用类似的方法快速生成δ无关集。在本文中，提出基于FP树快速生成δ无关集频繁项集精简表示模型。在文献[7]中，δ无关集具有反单调性质，如果一个项集不是无关集，则其超集不是无关集。这种性质非常适合使用深度优先策略生成。FMINEX算法对于每一个δ无关集都生成一个条件数据库，如果该项集不是无关集，则无需生成其条件数据库。

3.2具体算法

在FP树上挖掘项集X的时候，可以采用反单调思想。设项集X的条件数据库为Dx，其中Dx是所有频繁项为F，设a∈F，则a是频繁项，如果X∪{a}是频繁无关集，则a保留；否则如果项集X∪{a}不是无关集但是频繁的，则加入带频繁负向边界中，否则将a从F中除去。如果F中的元素超过1个，则继续这个过程，生成新的FP树。

在挖掘过程中，对于一个候选项集X是否频繁的判断是非常迅速的。由于对一个项集的判断需要使用其子集，所以一个项集生成之前，其子集必须首先生成。

算法FMINEX

输入：数据库D，最小支持度σ，最大无关值δ。

输出：频繁无关集FreqFree和边界BD-

1) S是一个频繁无关集

2) Ds是S的条件数据库

3) 扫描数据库Ds，得到所有的频繁项F，并且将这些频繁项进行降序排序F={F1，F2，…,Fn}

4)forallitema∈Fdo

5)ifFreq(S∪{a})>= σand∀X⊂S∪{a},X∈FreqFree,Y=RX,Freq(X)-Freq(X∪Y)<=δand∀X⊂S∪{a},X∈FreqFree

6)FreqFree=FreqFree∪(S∪{a})

7)elseifFreq(S∪{a}) >= σand

∃X⊂S∪{a},X∈FreqFree,Y=RX,

Freq(X)-Freq(X∪Y)>δand∀X⊂S∪{a},X∈FreqFree

8)BD-=BD-∪(S∪{a})

9)F=F-a

10)else

11)F=F-a

12)endfor

13)if|F| <=1

14)return

15)foralltransactiont ∈Ds

16)t=t∩F

17)将t中的项按照F中的排序进行排序

18)将所有的t重新生成一颗FP树

19)Endfor

20)forallitema∈Fdo

21)FMINEX(S∪{a},Ds∪{a},σ,δ)

22)Endfor

23)returnFreqFree∪BD-

FMINEX主要的输入参数是数据库D、最小支持度σ以及最大无关值δ，输出是频繁无关集和其对应的支持度，以及负向边界。由于FP树的生成是反复迭代的过程，在第1到第3步，是针对一个项集S，和其对应的条件数据库Ds。首先扫描数据库得到所有项的支持度集合F，并且按照降序进行排序。在第4步到第12步都是对S和F中的每一个项a组合而生成的项集(S∪{a})进行判断，在第5和第6步中，判断项集(S∪{a})是否是无关集，如果是，则加入到无关集中。在第7步到第9步，如果项集(S∪{a})是频繁的，并且所有的直接子集是无关集，而本身不是无关集，则将其加入到负向边界中，同时将a从F中删除。这就使用到了剪枝策略，因为不是无关集的超集肯定不是无关集。对于不满足第5步要求的项a都从F中删除，也使用到了剪枝策略。第13步和第14步判断集合F中的元素，如果个数小于等于1，则停止建立新的FP树。在第15到第19步是根据集合F中的结果建立新的FP树，第20步到22步，是对新建立起来的FP树递归调用本算法。最终返回无关集所有元素。

4实验结果对比以及分析

为了研究FMINEX算法的性能，实验对比了原算法MINEX和最新利用FP树结构的算法FPASCAL[1]。这3种算法都使用C++分别进行实现，运行的平台是WIN7，I5处理器，4G内存。实验对比内容包括时间、空间消耗情况。由于FMINEX算法和FPASCAL算法使用的是FP树，因此其占用的内存大小存在变化，而MINEX算法使用的是数据库，占用的内存一直不变。在对比实验中，所使用的数据集分别为chess、connect、pumsb、pumbs_star、T10I4D100K、T40I10D100K，这些数据集都可以从http://fimi.cs.helsinki.fi/data/中下载。

在实验中，代表精度误差的δ是一个很重要的参数，它代表了在实际使用过程中可以最大容忍的项集和其超集支持度误差的值。本文考察了当δ分别等于10、20、30的情况下，FMINEX和MINEX的运行效果。挖掘出来的δ无关集和文献[7]中一样，具体结果可参看文献[7]实验部分，而算法效率结果如下所示。而需要注意的是FPASCAL算法是无损压缩，δ对其生成的结果没有任何影响。MINEX算法在运行过程中将数据集全部存储在内存中，因此占用的空间不会随着支持度或δ的变化而改变, 一直保持不变。

当δ=10时，算法FMINEX和MINEX以及FPASCAL在chess数据集上运行的结果如图1所示。在图1(a)中可以很明显地发现FMINEX比MINEX至少快3倍，并且随着支持度的降低，性能优势更加明显。这是因为随着支持度降低，MINEX需要扫描数据库的次数加多，而FMINEX生成的FP树规模虽有变大，但是压缩效果明显，所以算法整体效率很高。而FPASCAL算法虽然是无损压缩，由于使用FP树结构，所以算法整体效率依然高于MINEX算法。

在图1(b)中，在刚开始的时候，FMINEX所占的空间比MINEX要大，这是因为当支持度较低的情况下，FP树需要存储的头表节点和树中的节点的数量较多，因此占用了很多的空间，但是随着支持度的增加，FP树的规模逐渐减少，比MINEX占用的空间少。而FPASCAL是无损压缩，需要占用的存储空间比FMINEX要大。

图1当δ=10时3种算法在chess数据集上运行比较结果

(a) 时间效率对比图；(b) 空间使用对比图

当δ=10的时候，算法FMINEX和MINEX以及FPASCAL在connect数据集上运行的结果如图2所示。在图2中可以很清晰地看出，无论是时间效率还是空间效率，FMINEX算法的性能均比MINEX算法要好。在图2(a) 中FMINEX比MINEX快至少30倍，并且随着支持度的降低，性能优势进一步明显。原因和在chess数据集上运行结果是一样的。在图2(b)中FMINEX比MINEX的空间使用量少5倍以上，并且随着支持度的增加，占用的空间进一步减少。这是因为connect数据集中的数据比较密集，压缩效果比较明显。FPASCAL算法是无损压缩，挖掘出的项集数量比无关集多，但是由于使用FP树结构，所以FPASCAL的时间和空间效率在这两种算法之间。

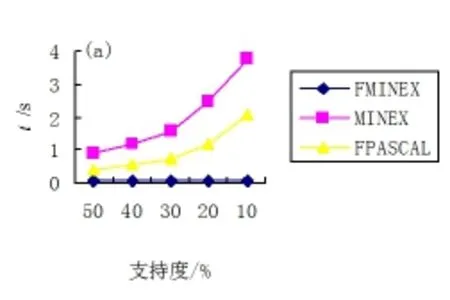
图2当δ=10时3种算法在connect数据集上运行比较结果

(a) 时间效率对比图；(b) 空间使用对比图

当δ=20时候，算法FMINEX和MINEX以及FPASCAL在pumsb数据集上运行结果如图3所示。在图3中可以很清晰地看出，FMINEX算法的时间和空间性能均比MINEX算法要好。在图3(a)中可以发现，算法FMINEX比算法MINEX的运行速度快3-6倍。在图3(b)中，可以看出FMINEX所占的空间比MINEX要少2-20倍。算法时间和空间效率优势的原因是pumsb是数据密集型数据集，FP树的压缩效果比较好。FPASCAL算法的性能表现在两种算法之间。

图3当δ=20时3种算法在pumsb数据集上运行比较结果

(a) 时间效率对比图； (b) 空间使用对比图

当δ=30的时候，算法FMINEX和MINEX以及FPASCAL在T10I4D100K和T40I10D100K数据集上运行结果如图4和图5所示。

在图4(a)和图5(a)中，算法FMINEX的运行速度比MINEX快2-3倍，PASCAL算法的速度介于两者之间。由于T10I4D100K和T40I10D100K是典型的数据稀疏型数据集，生成的FP树压缩效果不够好，和扫描数据库而得到支持度相比，FMINEX在FP树上优势并不明显。

在图4(b)和图5(b)中，算法FMINEX和FPASCAL在支持度比较低的时候，占用的空间均比MINEX大。这是因为T10I4D100K和T40I10D100K是典型的稀疏型数据集，在支持度比较低的情况下，压缩效果并不好。然而随着支持度的增加，在FP树中需要存储的头表节点和树中的节点的数量会减少，所以FMINEX和PASCAL所占的空间会小于MINEX。由于FPASCAL是无损压缩，因此所需要的存储空间比FMINEX多。

图4当δ=30时3种算法在T10I4D100K数据集上运行比较结果

(a) 时间效率对比图；(b) 空间使用对比图

5结束语

频繁项集数量过于庞大而导致的查询项集支持度的代价大的问题是频繁项集研究领域中的一个重要研究课题，无关集实现了在查询结果准确率和查询效率之间的折中，达到了以较小的支持度误差实现查询效率大幅提高的效果。针对无关集生成的效率不高的问题，本文提出在FP树快速挖掘无关集精简表示中所需要元素的算法FMINEX，实验结果证明，算法FMINEX的性能不仅比原有算法MINEX要好，而且比最新利用FP树结构的算法FPASCAL还要好。探讨如何在分布式环境下快速生成无关集精简表示成为以后研究的重点和方向。

参考文献:

[1] 许普乐, 张勤, 纪允. 基于FP树的一种快速挖掘生成器算法[J]. 安庆师范学院学报 (自然科学版), 2013，19 (1):48-53.

[2]HanJiawei，MichelineKamber．数据挖掘概念与技术[M]．范明，孟小峰，译．北京：机械工业出版社，2004：1-261.

[3] 田卫东，纪允. 一种频繁核心项集的快速挖掘算法[J]. 计算机工程, 2014, 40(6): 120-124.

[4] 纪允. 析取闭合项集的快速生成和恢复算法研究[D]. 合肥：合肥工业大学, 2013.

[5] 王创新. 关联规则提取中对Apriori算法的一种改进[J]. 计算机工程与应用, 2004, 40(34): 183-185.

[6]MannilaH,ToivonenH.Multipleusesoffrequentsetsandcondensedrepresentations:extendedabstract[C].Procofthe2ndInternationalConferenceonKnowledgeDiscoveryandDataMining(KDD’96), 1996: 189-194.

[7]BoulicautJF,BykowskiA,RigottiC.Free-sets:Acondensedrepresentationofbooleandatafortheapproximationoffrequencyqueries[J].DataMiningandKnowledgeDiscovery, 2003, 7(1): 5-22.

[8]AgrawalR,ImielińskiT,SwamiA.Miningassociationrulesbetweensetsofitemsinlargedatabases[C].ACMSIGMODRecord, 1993, 22(2): 207-216.

[9] 王艳, 李玲玲, 邵晓艳. 改进的频繁项集挖掘算法研究[J]. 计算机工程与应用, 2012, 48(19): 119-121.

[10] 张云涛, 于治楼, 张化祥. 关联规则中频繁项集高效挖掘的研究[J]. 计算机工程与应用, 2011, 47(3): 139-141.

[11] 王艳, 薛海燕, 李玲玲, 等. 一种改进的加权频繁项集挖掘算法[J]. 计算机工程与应用, 2010, 46(23): 135-137.

[12]HanJiawei,PeiJian,YinYiwen.Miningfrequentpatternswithoutcandidategeneration[C].ProcofACM-SIGMODInternationalConferenceonManagementofData,Dallas,USA:ACMPress, 2000:1-12.

AFastAlgorithmforMiningFreeSetsBasedonFPTree

XUPu-le1,JIYun2,ZHANGqin3

(1.Dean'sOffice,WuhuInstituteofTechnology,Wuhu,Anhui241006,China;2.TonglingBranch,ChinaMobileGroupAnhuiCompanyLimited，Tongling,Anhui244000,China;3SchoolofInformationandArt,AnhuiVocationalandTechnicalCollegeofForestry,Hefei,Anhui230031,China)

Abstract:Byintroducingfreesets,wesolvetheoverlargenumberofminedfrequentitemsetsindataminingandhighcostofgetexactlysupportofitemsetinspecificusingareaproblems.AnewalgorithmFMINEXisproposed,miningfreesetsfromFPtreewithapruningstrategywhichaimstosolvetheinefficientoftraditionalminingfreesetsmethod.ExperimentalresultstestifyFMINEXandshowabetterperformancebothintimeandspaceconsuminginminingprocess.

Keywords:datamining;frequentitemsets;freesets;FPtree;pruningstrategy

* 收稿日期：2014-07-09

基金项目：安徽省高等学校省级一般教学研究项目(20101264)。

作者简介：许普乐，男，安徽芜湖人，硕士，芜湖职业技术学院副教授，研究方向为数据挖掘、智能计算等。

中图分类号：TP311

文献标识码：A

文章编号：1007-4260(2016)02-0060-06

E-mial: jiyun1988@126.com

网络出版时间：2016-06-08 12:57网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160608.1257.015.html