不同糙率推求方法在引水隧洞中的对比分析
齐 英
(辽宁省沈阳水文局,辽宁沈阳110046)
不同糙率推求方法在引水隧洞中的对比分析
齐 英
(辽宁省沈阳水文局,辽宁沈阳110046)
摘要:文章以辽宁引兰入汤隧洞为研究实例,分别介绍了采用阻力系数计算方程和一维非恒定流数学方程2种方法推求引水隧道的糙率,并结合引水隧洞原型实测水位流量数据,对比分析2种糙率推求方法的适用性和计算精度。研究结果表明:一维非恒定流方程推算的糙率经反算的流量精度要好于采用阻力系数方程计算的糙率经过反推的流量精度。研究成果对于引水隧洞糙率推求和反算提供参考价值。
关键词:阻力系数;一维非恒定流;糙率推求;引水隧洞
1 概述
糙率推求的合理性对于引水隧洞的设计至关重要,因此对于引水隧洞的糙率推求也一直是国内外许多学者关注的热点问题。引水隧洞糙率推求计算较为复杂,与引水隧洞的断面形状、断面表面粗糙度以及引水渠道坡降等多种因素相关,因此引水隧洞的糙率推求一直是工程设计的一个技术难点。为此,国内外学多学者针对引水隧洞的糙率推求展开相关研究,并取得一定的研究成果[1-5]。在这些研究成果中,两种方程研究成果相对较多,分别为阻力系数计算方程和一维非恒定流数学方程。张景岳[6]运用阻力系数计算方程推算水电站引水隧洞衬砌段的糙率,研究结果表反推的糙率符合设计规范要求。张良然[7]采用阻力系数计算方程推算不同衬砌段的糙率,结论表明该方程具有较好的适用性。袁荣库[8]采用一维非恒定流数学方程结合发电隧洞水工模型试验,推求实验段的糙率,研究表明该方法较好的计算了隧洞的糙率。段琦琦[9]采用一维非恒定流数学方程计算计算了水库引水隧洞的糙率,研究表明该方法符合隧洞内水流流态的实际情况,适合于引水隧洞的糙率推求。综上研究成果表明阻力系数计算方程和一维非恒定流数学方程都可以推求隧洞的糙率,但是不同方法具有不同的适用性,为此,本文分别引入上述2种糙率推求方法,结合隧洞实测水位流量数据,对比分析不同糙率推求方法在引水隧洞糙率推求的适用性,研究成果对于引水隧洞的糙率推求提供参考价值。
2 不同糙率推求方法
2.1 阻力系数计算方程
美国陆军工程兵团在尼古拉兹试验实验基础上,通过大量实测数据进行统计对比分析,得到的阻力系数计算方程,该方程的表达式为:
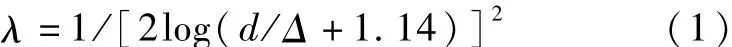
式中:Δ为隧洞的粗糙度,d为隧洞的管道直径,m。
方程(1)中需要计算隧洞粗糙度Δ,但是在实际工程设计,隧洞的粗糙度需要在引水隧洞施工完成后才可以确定。为了估算隧洞的粗糙度,在实际计算过程中,国内外许多学者大都采用经验公式进行估算,在已知隧洞直径的情况下按照以下经验方程估算隧洞的粗糙度,计算方程为:
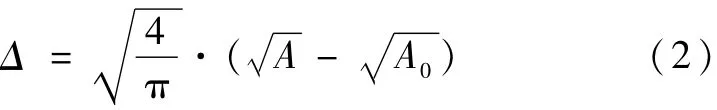
式中:A为隧洞的横断面面积,m2;A0为隧洞最小断面面积,m2。
将公式(2)代入公式(1)中,可得到糙率推求公式:
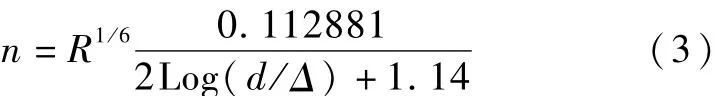
式中:R为隧洞断面水力半径,m。
2.2 一维非恒定流方程
运用一维非恒定流方程,构建引水隧洞非恒定流水力学数学模型,一维非恒定流数学模型的连续方程和运动方程分别为:

式中:A表示隧洞断面面积,m2;B表示隧洞断面水面宽,m;Q表示通过隧洞断面流量,m3/s;t表示构建模型的计算时间,h;q表示单位河长的旁侧入流,m3/s,本文设置为0;u表示隧洞断面平均流速,m/s;x表示隧洞内沿水流方向的水平距离,m;a表示隧洞断面流速分布不均匀系数;g表示重力加速度,m/s2;Z表示隧洞断面水位,m;Sf表示隧洞沿程水力比降,%。
运用有限差分方法对方程(4)进行离散,得到有限差分方程。
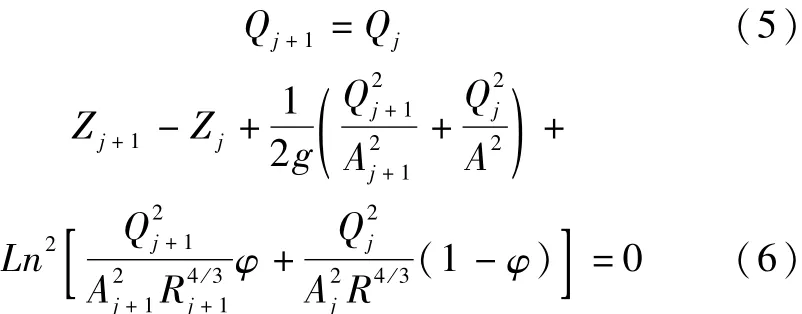
式(5)、(6)中:j表示计算断面的编号,L表示断面之间的距离,m,φ表示离散因子。
由上述方程可以得到糙率推求公式:
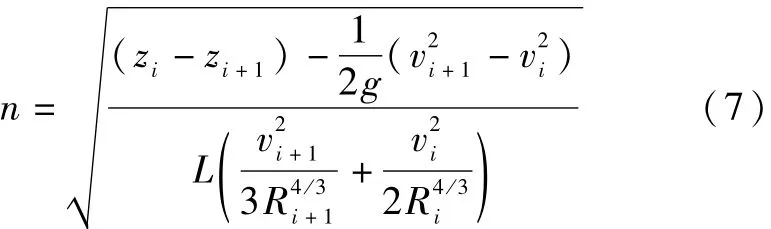
式中:Z为断面水位,m;V为断面平均流速,m3/s;R为水利半径,m;L的含义同方程(5)。
3 实例分析
3.1 引水隧洞原型观测实验布置
为分析2种糙率推求方法在引水隧洞的适用性,在引水隧洞内设置5处断面,各断面安置水位计和流量计,进行断面水位流量测定。在进行水位流量测定前,对5处断面进行了断面测量,获取断面面积、湿周以及水力半径。各断面在引水隧洞内的布置情况见图1。
3.2 不同糙率推求方法的对比分析
为对比不同糙率推求方法在引水隧洞的适用性,结合断面测量数据,分别采用阻力系数方程和一维非恒定流方程进行糙率的推求,并运用曼宁公式进行流量的推算,结合断面实测流量数据,对比不同糙率推求方法的计算精度,对比结果见表1和图2。
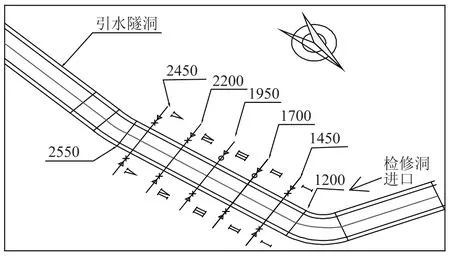
图1 断面布置示意图
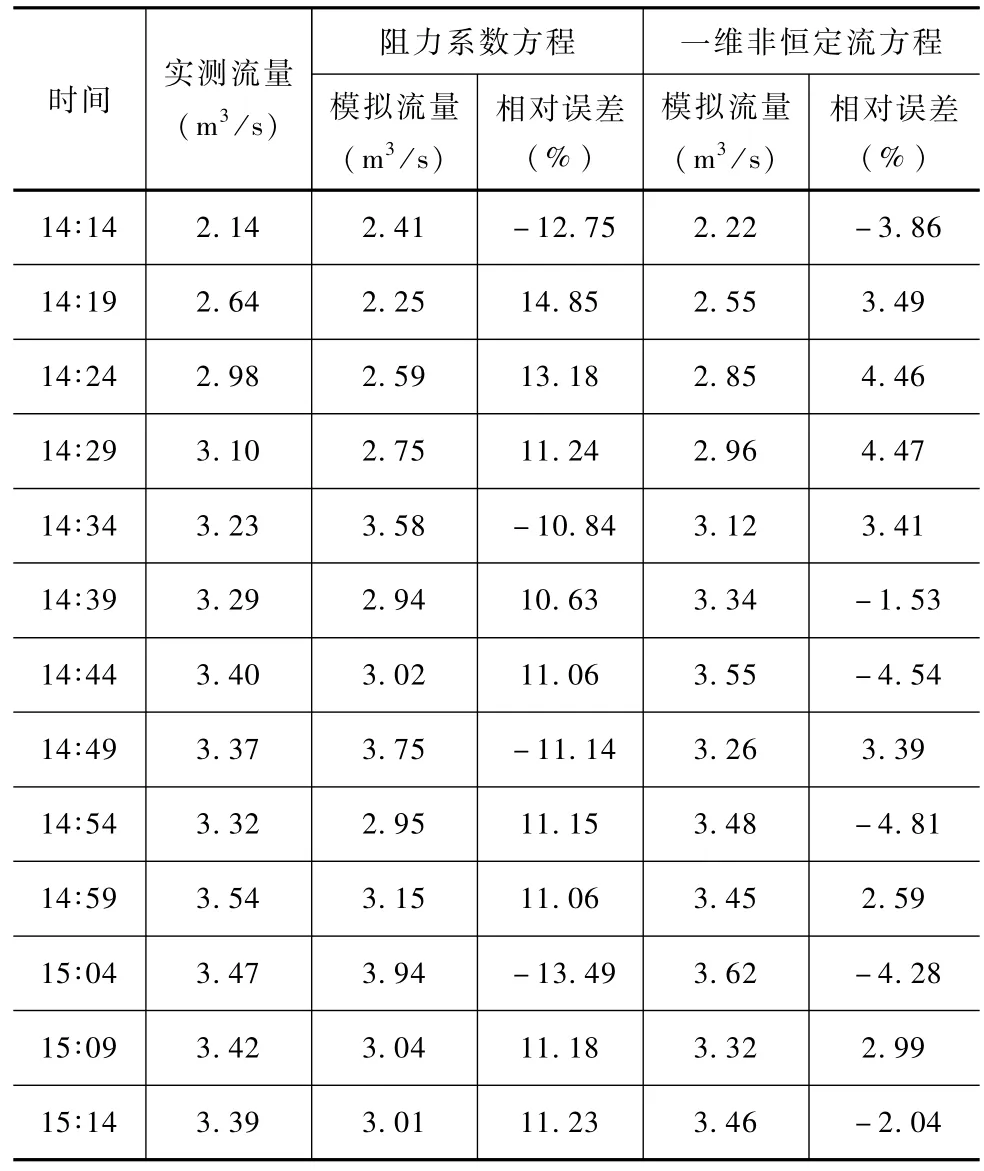
表1 不同糙率推求方法在引水隧洞中计算精度对比
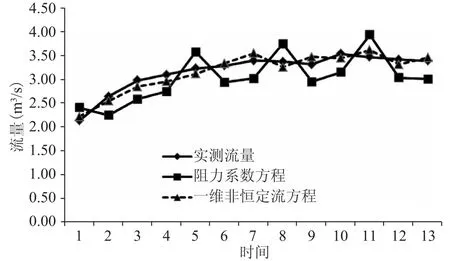
图2 不同糙率推求方法下反算流量和实测流量对比
表1为运用2种糙率推求方法推求不同水位流量下的隧洞糙率后,再结合曼宁公式反算断面流量,并和实测流量进行对比,以此来分析不同糙率推求方法在隧洞糙率推求的适用性及精度。从表1中可以看出,阻力系数方程计算的糙率经过曼宁公式反推的流量和实测的流量之间相对误差在10.63%~14.85%之间,相对误差在20%以内,符合糙率推求规范要求。一维非恒定流推算的糙率经过曼宁公式反推后的流量的实测流量之间的相对误差在-1.53%~4.81%之间,相对误差小于5%,也同样符合糙率规范推算的要求。但相比而言,一维非恒定流方程推算的糙率经反算的流量精度要好于采用阻力系数方程计算的糙率经过反推的流量精度。
图2为采用不同糙率推求方法反算的流量和实测流量对比图。从图中可以看出,一维非恒定流方程推算的糙率经反算的流量和实测流量吻合度明显好于阻力系数方程推算的糙率反推算的流量和实测流量的吻合度,这主要是因为阻力系数方程将隧洞内的水流假定为恒定流进行推算,而隧洞内的水流由于受到隧洞闸门开启高度和时间,流态基本上属于非恒定流,所以采用一维非恒定流方程推算的糙率较为符合实际情况。
综上,在引水隧洞内糙率推求中,一维非恒定流更适合于引水隧洞的糙率推求。
4 结论
本文分别采用阻力系数方程和一维非恒定流方程对引水隧洞内的糙率进行推求,并结合引水隧洞原型观测水位流量数据,对比不同糙率推求方法在引水隧洞糙率推求的适用性和推求精度,研究得出以下结论。
(1)2种方法推求的糙率经过曼宁公式反推的流量和实测流量之间的相对误差均小于20%,符合糙率推求的规范要求。一维非恒定流方程更符合引水隧洞实际水流情况,经反推的流量和实测流量相对误差明显好于阻力系数方程,更适合于引水隧洞的糙率推求。
(2)一维非恒定流方程需求断面地形数据较多,阻力系数方程需求断面地形数据相对较少,在工程实际设计时,应结合隧洞实际情况进行方法的选择。
参考文献
[1]陈文熙.基于一维非恒定流数学模型的辽宁省引水隧洞糙率推求研究[J].水利技术监督,2015(04):35-38+41.
[2]贾国华.装配式钢筋混凝土U型渠节水计量灌溉技术应用[J].水利技术监督,2011(05):62-64.
[3]沈军云,陈学林,刘涛.黑河莺落峡河段糙率分析及其计算[J].水利规划与设计,2011(04):42-45.
[4]任强.跨流域调水工程输水建筑物糙率研究[J].水利规划与设计,2010(03):43-45+65.
[5]吴疆,潘益斌.浅谈锦屏二级引水隧洞沿程糙率系数的反算方法[J].大坝与安全,2014(01):6-8.
[6]张景岳,霍吉才.水电站引水隧洞衬砌施工质量控制[J].水力发电,2009(03):77-78.
[7]张良然.不衬砌隧洞的糙率[J].水利水电科技进展,1997 (05):50-52.
[8]袁荣库,任玉平.弯弯川水电站引水发电隧洞水工模型试验研究[J].黑龙江水利科技,2012(11):4-5.
[9]段琦琦.长距离无压引水隧洞水气两相流数值模拟[D].天津大学,2008.
中图分类号:TV67
文献标识码:A
文章编号:1008-1305(2016)02-0038-03
DOI:10.3969/j.issn.1008-1305.2016.02.017
收稿日期:2015-08-14
作者简介:齐 英(1967年—),女,高级工程师。

