宽频激励下双稳态压电振动发电机供电能力分析

何青，　毛新华,2，　褚东亮

(1.华北电力大学 电站设备状态监测与控制教育部重点实验室，北京 102206；2.北京中丽制机工程技术有限公司，北京 101111)



宽频激励下双稳态压电振动发电机供电能力分析

何青1，毛新华1,2，褚东亮1

(1.华北电力大学 电站设备状态监测与控制教育部重点实验室，北京 102206；2.北京中丽制机工程技术有限公司，北京 101111)

摘要:为了探讨双稳态压电振动发电机在宽频激励下的供电能力问题，建立了宽频激励下双稳态压电振动发电机系统的动力学模型，仿真了双稳态压电振动发电机系统的输出响应特性和不同运动状态的输出电压特性，研究了双稳态压电振动发电机系统运行在高能量轨道上的激励条件，据此优化双稳态压电振动发电机结构参数，并对传感器网络节点的用电需求和双稳态压电振动发电机的供电能力进行分析。仿真和实验结果表明：双稳态压电振动发电机在宽频激励下，其输出平均功率为3.8 mW，能够满足实际振动环境下无线传感器网络节点的用电需求。

关键词:振动；宽频；能量收集；发电机；双稳态；动态响应

0引言

振动能量广泛存在于桥梁、汽车、输电导线、电厂旋转设备等各种环境中，利用振动能量采集技术将环境中的振动能量转换为电能，不仅可以为无线传感器网络节点等低功耗的电子设备供电，还可以减小振动对周围环境中结构的损伤和破坏[1-4]。但真实环境中振动的宽频特性与随机性使得传统压电振动发电机供电具有很大的局限性，当传统压电振动发电的频率与环境激励频率相差5%时，压电振动发电机几乎收集不到任何能量。双稳态压电振动发电机利用自身结构提供的非线性力，在宽频激励下的发电机系统产生跳跃现象，能极大拓展压电振动发电机的谐振带宽，提高宽频激励环境下的输出功率[5-6]。

目前，双稳态压电振动发电机因具有较宽的谐振带宽特性而成了振动能量收集领域的研究热点[7-8]。文献[9]利用一对磁铁为压电振动发电机提供非线性力，实现了宽频激励下的输出大幅响应，提高了压电振动发电机的谐振带宽；但只做了实验研究，没有对压电振动发电机运动的机理与本质特性进行分析。文献[10]建立了双稳态压电振动发电机系统的数学模型，分析了双稳态共振发生的频率条件和不同频率激励下的输出功率；但只考虑了弱周期激励下的频率变化情况，没有考虑激励幅值变化对输出电压的影响。文献[11]和[12]建立了磁力模型和压电悬臂梁发电机系统的集总参数模型,仿真了压电振动发电机的动态响应特性，并分析了频率变化和幅值变化对输出特性的影响；但文献中建立的集总参数模型有较大的模型误差，这对于输出功率原本不高的压电振动发电机在定量分析供电能力时所带来的误差将会更大。文献[13]研究了不同激励下双稳态振动发电机系统的非线性振动特性，从理论角度对压电振动发电机系统的幅值跳跃、多解现象进行了释疑；但未考虑激励的幅值阈值对输出特性的影响。振源的频率变化和幅值变化相互交织影响着双稳态压电振动发电机的输出特性和供电能力；而上述这些研究涉及这些方面的分析较少，尤其是针对实际宽频激励环境下的供电能力分析更少[14-16]。

本文建立了带有修正参数的双稳态压电振动发电机的集总参数模型，通过数值方法仿真了压电振动发电机的输出特性和不同运动状态下的输出电压特性，研究了双稳态压电振动发电机在高能量轨道上运行的激励条件，并优化了压电振动发电机的结构参数，分析了双稳态压电振动发电机在宽频激励下的供电能力，为双稳态压电振动发电机的设计与实际应用提供了理论指导。

1双稳态压电振动发电机的动力学模型

双稳态压电振动发电机的结构类型很多，其中，悬臂梁式双稳态压电振动发电机以结构简单、体积小、成本低、易于微型化等优点成为压电振动发电机主流结构，其结构如图1所示。该结构由支架A、金属悬臂梁B、压电陶瓷片P(PZT)、外部磁铁C和D组成。PZT压电陶瓷片粘贴在悬臂梁的根部，压电陶瓷片上引出的两个电极与外接负载电阻RL相连接。悬臂梁的长度、宽度、厚度分别表示为L、b、h,压电片的长度、宽度、厚度分别表示为Lp、bp、hp，磁铁C和磁铁D的间距为d，悬臂梁固定端到磁铁中心的距离为l，悬臂梁的质量为mb，压电片的质量为mp，外部磁铁质量均为mc。在振源的激励下，悬臂梁产生谐振而引起PZT压电陶瓷形变，依据压电效应而在压电陶瓷的两端产生电压，可将环境的振动能转换为电能。当两个磁铁的间距在合适位置时，悬臂梁式压电振动发电机表现为双稳态特性。

图1　双稳态压电振动发电机结构图Fig.1　Bistable piezoelectric vibration generator　　　 diagram

悬臂梁式压电振动发电机的运动形式主要是以一阶模态为主，其动力学模型可简化为集总参数模型；但集总参数模型带来的误差较大，故引入修正参数κ1，以平衡模型误差。根据双稳态压电振动发电机结构的受力分析和牛顿第二定律，双稳态压电振动发电机系统的力学方程[17-20]为

(1)

其中：X为悬臂梁末端磁铁的振动位移；V为压电陶瓷片两端产生的电压；M,c,k为压电悬臂梁的等效质量、等效阻尼和等效刚度；Fc为磁力在振动方向上的分量；α为机电耦合系数；κ1为集总参数模型的修正系数；P(t)=MAsin(Ωt)假设为正弦激励，t为时间。等效质量M、等效阻尼k、等效刚度c、磁力分量Fc、机电耦合系数α和集总参数模型的修正系数κ1分别由下列方程计算给出。

(2)

(3)

(4)

(5)

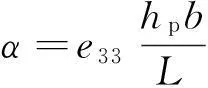
(6)

(7)

根据基尔霍夫电流定律，双稳态压电振动发电机的电学方程如下：

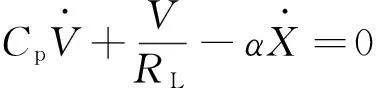
(8)

其中Cp为压电陶瓷的等效电容，其计算公式为

(9)

将式(2)～式(7)分别代入式(1)，式(9)代入式(8)中，对代入结果进行无量纲化处理，则新的动力学方程可变为：

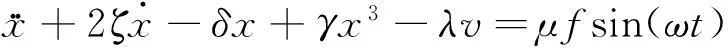
(10)

(11)

(12)

2输出性能仿真分析与结构优化

2.1输出响应特性仿真分析

仿真所需参数取值为：η=0.02，e31=-5.35 N/mV，双稳态压电振动发电机结构的参数如表1所示。为获得宽频激励下双稳态压电振动发电机的输出响应特性，分别以激励的频率变化和幅值变化为变量，采用数值方法求解状态方程式(12)，得到频率变化、幅值变化时的分岔图。

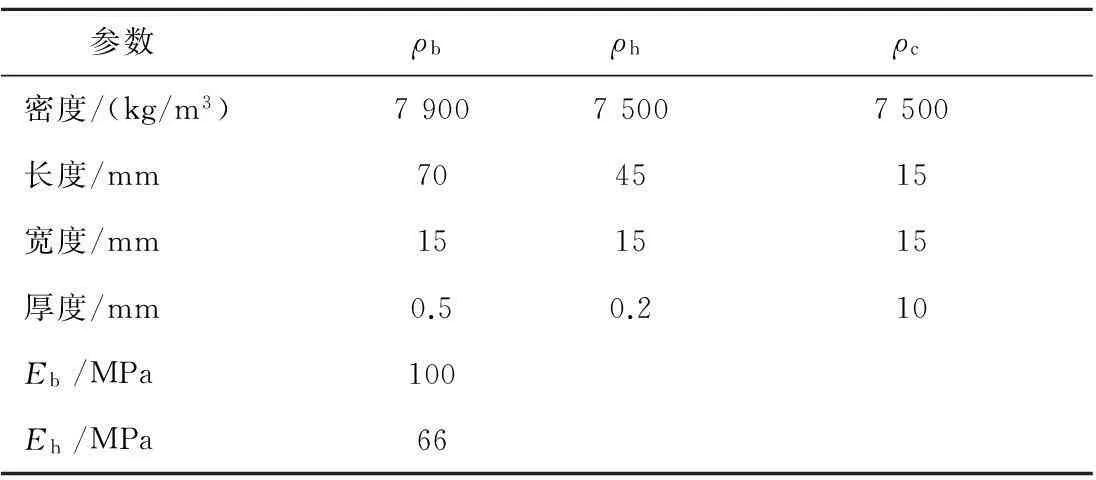
表1　压电振动发电机参数

当无量纲激励幅值大于等于0.409时，系统能够产生大幅周期运动，如图2(b)～(d)，且从单个频率分岔图看，随着激励频率的增加，系统先后经历单阱内小幅周期运动、双阱间大幅周期运动、倍周期运动、双阱间大幅混沌运动，最后又回到单阱内做小幅运动。产生这种现象的原因是当激励频率较低时，系统获得的能量也较低，不足以跨越系统的幅值阈值，而只能在某一势阱内做小幅运动，此时双稳态压电振动发电机在低能量轨道上运行。随着激励频率的增大，系统获得足够的能量越过幅值阈值而产生大幅运动，此时双稳态压电振动发电机在高能量轨道上运行。而当无量纲激励幅值小于0.409时，如图2(a)，系统不能产生大幅周期运动，从单个激励频率分岔图看，系统在经历单阱内小幅周期运动后直接进入倍周期运动，然后进入混沌运动和单阱小幅运动。

分析图2可知，不论激励幅值大小如何，随着激励频率的增加，系统最终都又回到单阱内做小幅周期运动，这是因为激励频率增大的同时，系统的幅值阈值也在增加，当激励频率增大到一定值时，系统此时的能量又将低于新的幅值阈值，双稳态压电振动发电机又只能在势阱内做小幅运动。这表明系统发生大幅响应运动不仅有下限的激励频率阈值，而且还有上限激励频率阈值。

图2　激励频率分岔图Fig.2　Excitation frequency bifurcation diagram

分析如图3所示的单个激励幅值的分岔图可知，当无量纲激励幅值大于幅值阈值时，系统在势阱间发生大幅响应运动，且随着激励幅值增加，系统一直保持大幅输出响应运动。这表明双稳态振动发电机系统只有下限激励幅值阈值没有上限激励幅值阈值。比较图3(a)与图3(b)可知，激励频率越低时，系统发生大幅运动所需要的激励幅值也越小。

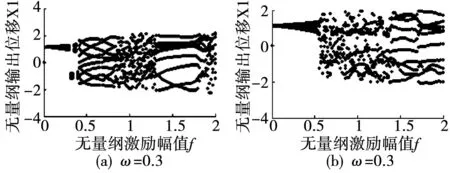
图3　激励振幅分岔图Fig.3　Excitation amplitude bifurcation diagram

2.2不同运动状态的电压输出特性

图4为无量纲激励幅值等于0.409时，压电振动发电机不同运动状态下的输出电压特性。分析图4可知：小幅周期运动和倍周期运动的输出电压都比较低，其峰值电压低于3 V，无法给无线传感器节点供电。大幅周期运动和混沌运动的输出电压较大，其峰值电压大于3 V，可以为无线传感器节点供电。根据式(13)，计算得到大幅周期运动状态下输出电压的有效值为8.7 V，混沌运动状态下输出电压的有效值为4.3 V。这说明，大幅周期运动状态的供电能力高于混沌状态下的供电能力。

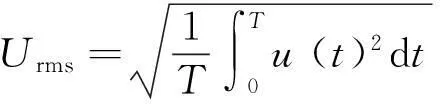
(13)

图4　f=0.409时，不同运动状态的输出电压Fig.4　System output voltage of the different　　　 behavior when f=0.409

3.3结构参数对激励幅值阈值的影响分析

双稳态压电振动发电机的势能方程可表述为式(14)所示，根据文献[21]的研究结果，振源激励的幅值阈值Ac与振源频率ω之间的关系如式(15)所示。

(14)

(15)

激励幅值分岔图仿真结果表明，只有当激励幅值大于系统要求的最低激励幅值(幅值阈值)时，双稳态压电振动发电机才能获得大幅输出响应。由式(15)知，系统结构参数恒定时，不同激励频率有着不同的幅值阈值，且幅值阈值随着激励频率的增大而增大；而在实际的振动环境下，频率较高时振幅一般往往较低，这使压电振动发电机谐振带宽变小，降低了宽频振动能量收集效率。

优化双稳态压电振动发电机结构参数，降低系统的幅值阈值，进一步扩大双稳态压电振动发电机的谐振带宽，可提高宽频振动能量收集效率。图5为不同结构参数的双稳态压电振动发电机所对应的幅值阈值随频率变化的关系。该图表明，悬臂梁的长度和刚度对激励幅值的阈值影响较大，长度越长或者刚度越小，发生大幅响应运动所需要的幅值阈值越低，越有利于收集低幅值的宽频振动能量，而悬臂梁的宽度和厚度对幅值阈值的影响较小。

图5　结构参数对幅值阈值的影响Fig.5　Influence of structure parameters on　　　 the amplitude threshold

3实验测试及供电能力分析

3.1实验测试验证

为验证仿真结果，构建了如图6所示的压电振动发电机实验测试系统。测试系统由SPF05函数信号发生器、GF-10型功率放大器、ZJY-601激振台、BVM-200测振表、加速度传感器、数据采集卡、DS1102C数字存储示波器等仪器和设备组成。实验原理为：SPF05函数信号发生器产生宽频信号，经GF-10功率放大器的输出到ZJY-601激振台进行振动控制，调节信号频率和功率放大器的输出振幅，用振动计测得激振台的频率和振幅，以模拟宽频激振环境。将能量采集器固定在激振器上，观察并记录示波器输出电压波形与数值，并计算出不同负载时的输出功率。实验结果如图8、图9所示。

图8为激励幅值变化时，双稳态压电振动发电机输出电压变化规律。结果表明：双稳态压电振动发电机系统存在幅值阈值，只有当激励幅值大于幅值阈值时，系统才能发生大幅响应，才能在高能量轨道上运行，输出电压才较大。而且激励频率越大，幅值阈值也越大，同时幅值阈值只有下限没有上限，这与3.1仿真结果相一致。

图6　实验平台Fig.6　Experimental platform

图7　实验装置与样机Fig.7　Experimental facility and prototype

图8　不同激励时系统的输出电压Fig.8　System output voltage under different　　　excitation

图9(a)为激励频率变化时双稳态压电振动发电机输出电压变化规律。结果表明：当激励频率在33～55 Hz时，压电振动发电机的输出端的峰值电压大于3 V，而在其余频段压电振动发电机几乎没有电压输出。这表明双稳态压电振动发电机系统存在频率阈值，而且该频率阈值既有下限值也有上限值。根据图9(a)的实验数据和式(13)、式(16)，可求得不同负载值的输出功率，如图9(b)所示。分析图9(b)可知，双稳态压电振动发电机的输出功率与负载大小相关，负载越大，输出平均功率越低。当激励频率在33～55 Hz范围内、负载为150 kΩ时，可计算出双稳态压电振动发电机在该频段内的平均输出功率约为3.8 mW。

(16)

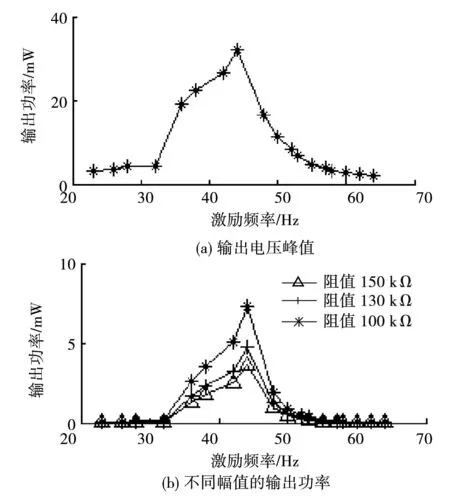
图9　双稳态压电振动发电机的输出电压和功率Fig.9　Output voltage and power of bistable　　　piezoelectric vibration generator

3.2供电能力分析

压电振动发电机输出的电压是交流电压，为了给低功耗的传感器节点提供稳定的电能，常采用能量收集电路模块LTC3588-1对压电振动发电机输出的电压进行整流、滤波、模数转换等调理，输出的稳定电能再由超级电容储存，以备供传感器节点使用。

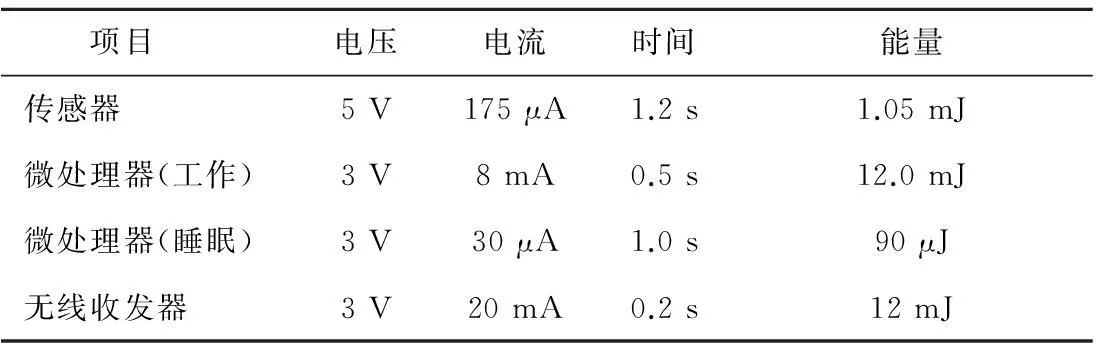
表2　传感器节点电路能量消耗情况

应用于监测系统的传感器网络节点系统主要包括加速度传感器、微处理器、射频无线收发器等器件，各器件的平均耗能情况[22-23]如表2所示。根据表2，传感器网络节点串联负载约为130 kΩ,发射一次信息需要的功耗为20 mJ。如果监测系统间隔1分钟采集发射一次信息，双稳态压电振动发电机1分钟内收集到的能量平均约为228 mJ，能够满足传感器网络节点的用电需求。

4结论

1)外界的激励条件决定着双稳态压电振动发电机的输出特性，只有当外界激励大于系统的频率阈值和幅值阈值时，双稳态压电振动发电机才能发生大幅响应运动，双稳态压电振动发电机才能在高能量轨道上运行。

2)双稳态压电振动发电机的结构参数与系统阈值的大小密切相关。对于悬臂梁式的压电振动发电机，增大悬臂梁的长度或者降低压电振动发电机的刚度，能够有效降低系统的幅值阈值，有利于收集宽频、低幅的振动能量。

3)双稳态压电振动发电机具有较大的谐振带宽和较高输出功率，能够满足传感器网络节点用电需求，解决了实际振动环境下传感器网络节点供电问题。

参 考 文 献:

[1]陈仁文．新型环境能量采集技术[M]．北京：国防工业出版社，2011:1-10．

[2]邱清泉, 肖立业, 辛守乔,等. 微型振动式压电发电机的设计与特性分析[J]. 电机与控制学报, 2011, 15(7):1-7.

QIU Qingquan,XIAO Liye，XIN Shouqiao，et al. Design and performance analysis for micro piezoelectric vibration generator [J]. Electric Machines and Control, 2011, 15(7):1-7.

[3]何青，毛新华，褚东亮．随机激励下双稳态压电振动发电机的振动特性[J]．噪声与振动控制，2015,35(2)：36-40．

HE Qing, MAO Xinhua, CHU Dongliang. Dynamic characteristics of a bistable piezoelectric vibration generator under random excitation [J]. Noise and Vibration Control, 2015,35(2):36-40．

[4]宾洋,杨东超，陈娜娜，等. 新型压电驱动机电耦合动力学系统分析与建模[J]. 电机与控制学报, 2008, 12(2):179-183.

BIN Yang, YANG Dongchao, CHEN Nana, et al. Analysis and modeling of a novel piezo-actuated electromechanical coupling dynamic system[J]. Electric Machines and Control, 2008, 12(2): 179-183.

[5]闫震,何青. 激励环境下悬臂梁式压电振动发电机性能分析[J]. 中国电机工程学报,2011,31(30): 140-145．

YAN Zhen, HE Qing. Performance analysis on incentive environment of micro cantilever piezoelectric vibration generator [J]. Proceedings of the CSEE, 2011, 31(30): 140-145.

[6]刘祥建,陈仁文. 压电振动能量收集装置研究现状及发展趋势[J]. 振动与冲击,2012,31(16): 169-175.

LIU Xiangjian，CHEN Renwen．Current situation and developing trend of piezoelectric vibration energy harvesters[J]．Journal of Vibration and Shock，2012,31(16):169-175.

[7]袁江波，谢涛，单小彪，等．复合型悬臂梁压电振子振动模型及发电试验研究[J]．机械工程学报，2010，46(9)：87-92.

YUAN Jiangbo，XIE Tao，SHAN Xiaobiao， et al．Vibrated model and experiments of multiple piezoelectric cantilevers in energy harvesting [J]. Journal of Mechanical Engineering，2010，46(9)： 87-92.

[8]HAME R L,WANG K W.A review of the recent research on vibration energy harvesting via bistable systems [J]. Smart Materials & Structures，2013,(22):1-12．

[9]TANG L, YANG Y, SOH C K. Improving functionality of vibration energy harvesters using magnets [J]. Journal of Intelligent Material Systems & Structures, 2012, 23(13): 1433-1449.

[10]ZHENG R, NAKANO K, HU H, et al. An application of stochastic resonance for energy harvesting in a bistable vibrating system [J]. Journal of Sound & Vibration, 2014, 333(12): 2568-2587.

[11]孙舒，曹树谦．稳态压电悬臂梁发电系统的动力学建模及分析[J]．物理学报，2012，60(21):103- 114．

SUN Shu，CAO Shuqian．Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system[J]．Acta Physica．Sinica，2012，60( 21) : 103-114．

[12]陈仲生，杨拥民．悬臂梁压电振子宽带低频振动能量俘获的随机共振机理研究[J]．物理学报，2011,6(7)：1-7．

CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wideband and low frequency vibration energy harvesting based on piezoelectric cantilever beams [J].Acta Physica Sinica,2011,6(7):1-7．

[13]贾尚帅，孙舒，李明高．基于谐波平衡法的双稳态压电发电系统非线性振动特性研究[J]．振动与冲击,2014,33(6):170-173.

JIA Shangshuai, SUN Shu, LI Minggao. Non-linear vibration analysis of bistable piezoelectric power generation system based on harmonic balance method [J]. Journal of Vibration and Shock, 2014, 33(6): 170-173.

[14]FOISAL A R M, HONG C, CHUNG G S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever [J]. Sensors & Actuators A Physical, 2012, 182(15): 106-113.

[15]TEHRANI M G,ELLIOTT S J.Extending the dynamic range of an energy harvester using nonlinear damping [J]. Journal of Sound & Vibration, 2014, 333(3):623-629.

[16]崔岩，王飞，董维杰，等．非线性压电式能量采集器[J]．光学精密工程，2012,20(12):2737-2743．

CUI Yan，WANG Fei，DONG Weijie，et al. Nonlinear piezoelectric energy harvester [J]. Optics and Precision Engineering，2012,20(12): 2737-2743．

[17]高毓璣，冷永刚， 范胜波，等．弹性支撑双稳压电悬臂梁振动响应及能量采集研究[J]．物理学报，2014,63(9)：1-13.

GAO Yuji， LENG Yonggang，FAN Shengbo，et al. Studies on vibration response and energy harvesting of elastic-supported bistable piezoelectric cantilever beams [J]. Acta Physica Sinica,2014,63(9):1-13.

[18]陈仲生，骆彦廷，杨拥民．非线性压电振动能量俘获行为建模及其不同参数影响机理研究[J]．国防科技大学学报，2013,35(2)：154-158．

CHEN Zhongsheng，LUO Yanting，YANG Yongmin. Modeling of nonlinear piezoelectric vibration energy harvesting behaviors and the effects of its different parameters [J]. Journal of National University of Defense Technology，2013,35(2): 154-158．

[19]李海涛，秦卫阳．双稳态压电能量获取系统的分岔混沌阈值[J]．应用数学和力学,2014,35(6):652-662.

LI Haitao，QIN Weiyang.Bifurcation and chaos thresholds of bistable piezoelectric vibration energy harvesting systems [J]. Applied Mathematics and Mechanics, 2014, 35(6): 652-662.

[20]韩研研，曹树谦，孙舒，等．考虑几何非线性时双稳态压电悬臂梁响应分析[J]．压电与声光，2014,36(1)：132-139．

HAN Yanyan，CAO Shuqian，SUN Shu，et al. Response analysis of bistable piezoelectric cantilever beam considering geometric nonlinearity [J]. Piezoelectrics & Acoustooptics，2014,36(1): 132-139．

[21]王嘉赋，刘锋，王钧义，等．随机共振系统输入阈值的频率特性[J]．物理学报，1997,46(12)：2305-2312．

WANG Jiafu，LIU Feng，WANG Junyi，et al．Frequency characteristics of the input thresholds of stochastic resonant systems[J]．Acta Physica Sinica，1997,46(12)：2305-2312．

[22]陈绍伟，王子，魏刚．基于压电能量收集技术的无线传感器节点设计[J]．计算机测量与控制,2014,22(3)：952-955．

CHEN Shaowei，WANG Zi，WEI Gang．Design of wireless sensor node based on piezoelectric energy harvesting technology[J]．Computer Measurement & Control, 2014,22(3)： 952-955．

[23]孟庆春，陈光柱．自供电无线传感网络节点设计[J]．仪表技术与传感器,2012,(7)：102-104．

MENG Qingchun,CHEN Guangzhu．Design of self-powered wireless sensor network node [J]. Instrument Technique and Sensor,2012,(7): 102-104．

(编辑：张楠)

Power supply capability analysis of piezoelectric vibration generator with bistable under wide frequency excitation

HE Qing1,MAO Xin-hua1，2,CHU Dong-liang1

(1.Key Laboratory of Condition Monitoring and Control for Power Plant Equipment,North China Electric Power University，Beijing 102206，China; 2.Beijing Chonglee Machinery Engineering Co.,Ltd,Beijing 101111,China)

Abstract:In order to explore a piezoelectric vibration generator with bistable supplying power for the wireless sensor node under wide frequency excitation, dynamical model under random vibration excitation was built. And accordingly the piezoelectric vibration generator was simulated with bistable output response and voltage under different motion state. The incentive condition of the piezoelectric vibration generator was explored with bistable running in high energy orbit.Structure parameters of the piezoelectric vibration generator with bistable were optimized.Electricity demand of sensor network nodes and power production ability of piezoelectric vibration generator with bistable were analyzed.The results of imitation and experiment indicate that the output average power of the piezoelectric vibration generator with bistable is about 3.8 mW under the specific frequency band excitation. It is able to meet the power demand of the wireless sensor network node.

Keywords:vibration; wide frequency; energy harvesting; generator;bistable; dynamic response

收稿日期:2015-06-15

基金项目：中央高校基本科研业务费专项资金资助项目(13XS13)

作者简介：何青(1962—)，男，博士，教授，博士生导师，研究方向为电力设备状态监测与故障诊断； 毛新华(1975—)，男，博士研究生，研究方向为电力设备状态监测与故障诊断、振动能量收集； 褚东亮(1984—)，男，博士研究生，研究方向为电力设备状态监测与故障诊断。

通信作者:毛新华

DOI:10.15938/j.emc.2016.07.003

中图分类号:TM 619

文献标志码:A

文章编号:1007-449X(2016)07-0017-07