水平管气液两相分层流界面剪切预测研究进展
郑平,赵梁(辽宁石油化工大学石油天然气工程学院,辽宁 抚顺 113001)
综述与专论
水平管气液两相分层流界面剪切预测研究进展
郑平,赵梁
(辽宁石油化工大学石油天然气工程学院,辽宁 抚顺 113001)
摘要:水平管气液两相分层流虽流型简单,但由于界面存在复杂的动量和能量传递,分层流的界面剪切预测至今没有一致的结论。本文从理论模型、实验模型、数值计算 3个角度出发,详细阐述水平管气液两相分层流界面剪切预测的研究现状,得出不同研究方法的优势和缺陷。针对 3种研究方法,指出理论模型通过模型简化和经验关联式来建立封闭模型,实验模型则在封闭关系上修正经验关联式,但由于简化假设和实验条件的限制,使得这两种研究方法对界面剪切应力的预测具有一定的局限性;数值计算能够弥补机理模型在流场细节等方面的不足,但能够提供界面剪切预测或封闭关系的工作很少。此外,对比了 5种不同形式的已有模型对气液两相分层流持液率和压降预测的结果。最后展望了水平管气液两相分层流界面剪切预测的研究趋势,提出理论和实验研究需要提出更详细的局部模型,并考虑工程实际工况进行研究,发展针对气液界面计算的新方法,并为分层流提供封闭关系则是数值计算研究面临的挑战。
关键词:水平管;气液两相流;分层流;界面剪切应力;持液率;压降
第一作者及联系人:郑平(1973—),女,博士,副教授,主要从事多相流体力学应用研究。E-mail zhengping0413@163.com。
水平管气液两相分层流是指存在密度差的两相流体,在质量力(如重力或其他惯性力)作用下,密度较大的相在下层流动,密度较小的相在上层流动,相界面存在清晰可辨的薄膜[1-2]。水平管气液两相分层流是化工工程和石油天然气工程中最常见的两相流流型之一,分层流的特点是流场除受到气壁和液壁的剪切作用外,还受到气液界面相互作用的影响。由于气液界面存在复杂的动量和能量传递,因此目前对分层流界面剪切应力的预测至今没有一致的结论。持液率和压降是分层流研究中最重要的两个参数,而气液界面剪切应力的计算与分层流持液率和压降的预测密切相关,对工程实际应用具有重要意义。
理论、实验和数值计算是研究水平管分层流界面剪切预测的3类基本方法。理论建模和实验的间接测量都是在尝试分析界面相互作用机理基础上提出不同的计算模型,因此也被称为机理性模型[3],机理性模型的共同特点是需要人为提供与经验关系同样数量的本构关系式。数值计算即计算流体力学(computational fluid dynamics,CFD)方法,通常依赖理论和实验的结果,在机理性模型的支持下深入观察流场细节特征,但讨论气液界面剪切应力本构关系的工作并不多。
本文从理论、实验、数值计算3类基本方法入手,对气液两相分层流界面剪切预测问题进行综述,通过对比分析5种已有模型得到的持液率和压降结果,找出各自的优势与缺陷,提出此问题的研究方向和展望。
1 气液两相分层流界面剪切预测理论
气液两相分层流的理论模型从数学模型和几何模型两方面论述。
1.1 数学模型
目前,已经建立了两类数学模型,即整体模型和与之互补的局部模型[4]。
早期的两相流模型对两相流动作了很大程度的简化假设,如最早提出水平管分层流压降和持液率的LOCKHART等[5]修正公式,此模型通过单相流模型计算两相流流动,适应性差,所以预测准确率偏低。
TAITEL等[6-7]建立了一维两流体模型,该模型假设气液界面为水平的光滑壁面,从而将气相流动假设为单相流,气壁和气液界面具有相同的摩擦因子,同时假设液相为明渠流动,相界面为一水平面,为此对气、液两相分别建立动量方程,这是整体模型的典型代表,许多理论模型及实验都建立在这一模型之上。但它忽略了流场的结构细节,对于大雷诺数湍流,通过平均速度前提下的经验关系式计算剪切应力往往偏小。因此该模型适用于层流和雷诺数较小的湍流分层流[8]。
HANSEN等[9]建立了二维移动壁面数学模型,通过双对数律速度分布假设和界面的无滑移自由移动壁面假设,按照近壁速度分布规律分析,针对界面光滑和波动两种情形,得到了平稳湍流的气液两相流流场分布规律。计算结果与实验相对比表明,二维移动壁面模型可以较好地预测光滑分层流和波状分层流,但是对后者的气液界面速度分布预测效果较差。
ULLMANN等[10-11]对层流分层流和湍流分层流(光滑与波状分层流)建立的封闭关系,是在TAITEL& DUKLER的动量方程基础上,结合已有的模型结果导出的半理论半经验分层流封闭关联式。但是,由于已有的不同模型对界面和液壁剪切应力的预测偏差很大,必然导致关联式在一定条件下(如当界面和液壁剪切应力预测同时偏高时)不能准确预测持液率。
两流体模型的缺陷在于将分层流看作叠置的两相分离的流动,其界面波动的幅度小于界面厚度,减弱了预测效果。为此,KANG等[12]将气液界面剪切应力视为附着于光滑界面的剪切和由波浪移动形成的剪切的总和,提出了剪切应力预测关联式。为了简化模型,此模型只考虑界面波附近流动分离较弱的情形,因此只适用于波动现象相对稳定的分层流。此外,对界面形状和界面速度分布形式,此模型并没有考虑。
LINÉ等[4]发展了一种局部两流体模型来计算气液界面的波动区域,他们并不预测界面形状,而是将界面假设为一已知的先验情形,该模型用于计算界面由压强和黏性剪切分布造成的动量传递。波动理论在分层流流动行为研究中的应用也是实验的重要课题之一,但对波动产生、变形、传播机理以及波动上下的湍流区域并没有进行分析。
刘夷平等[13]分析了液壁、气液间剪切应力预测的不确定度,并利用最大不确定度原理,对影响其准确度的各因素进行误差分析,修正了ANDRITSOS等[14]的实验模型。结果表明,气相摩擦因子可以用单相流的指数关系式表示,而液相摩擦因子受气液相界面剪切应力的影响较大。
1.2 几何模型
TAITEL & DUKLER模型是基于水平界面几何模型建立的数学模型,对于液相表观速度不大或弯管处的低持液率问题,由于BOND数减小,一些学者提出了非水平面几何模型,着重考察横向界面形状对分层流封闭模型的可能性。
HART等[15]将液相横截面区域处理为均匀厚度、紧贴管底的凹面,而 CHEN等[16]以及之后的VLACHOS等[17-18]将液相横截面区域处理为双圆交叉形成的月牙形,见图 1。这些非水平界面模型很大程度上弥补了早期理论模型在低持液率分层流的预测误差。
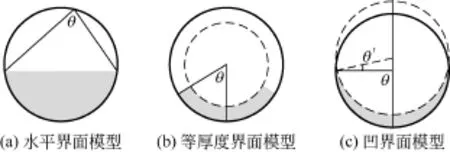
图1 分层流几何模型示意图
水平界面几何模型应用范围比较广,等厚度和凹形界面几何模型通常用于低持液率问题,凹形界面问题在讨论半环状流时非常有效,对于非牛顿流体分层流,凹形界面和与之对应的凸形界面几何模型都有广泛的研究[19]。
BRAUNER等[20]在预测界面形状时考虑了能量,并分析了液体的物性、持液率、管道尺寸、壁面附着力和重力对界面形状的影响。界面曲率预测提供了完美解决弯曲界面分层流所需的封闭关系式。后来,结合BRAUNER等[21]的流动关系式,又得到了一系列层流两流体系统界面形状和相关的局部和整体流动特性[22-23],但只准确地分析了二维层流分层流的流速情况。1998年,BRAUNER等[24]发展了一种基于弯曲气液界面的两流体模型,确定界面曲率与给定操作条件下持液率的封闭关系式。此模型能够对持液率和压降提供一种可靠的预测,对于湍流流动,此两流体模型的结果更准确。但当两流体模型在反常的高黏度环境中应用时,会发生最大的误差。
ROVINSKY等[25]对完全偏心的核心环形层流两相流进行了研究,用解析法求出持液率和压降。结果表明,当黏性相与管壁之间的连接区域增大时,润滑相面的形状就可能是凸形,这时压降减小的潜能会进一步减小。
SOLEIMANI[26]通 过 数 值 方 法 计 算 YOUNG-LAPLACE方程,确定液-液系统界面形状。结果表明,界面形状取决于接触角、BOND数和两流体当地体积分数的比率。
此外,非线性理论气液两相流界面特性(如界面波与不稳定性)的研究成果很有价值[16,27-29],这些方法不仅为建立更接近实际情况的理论模型提供依据和思路,也为实验数据处理提供了方便有效的方法。
2 气液两相分层流界面剪切预测实验
理论与实验相结合一直是研究水平管气液两相分层流界面剪切预测的主要方法,测量方法和数据处理是实验的基本内容,理论模型通常由实验对比结果得到合理解释。
KOWALSKI[30]测量了空气-水和氟利昂 12-水系统的气壁和液壁剪切应力,得出新的壁面摩擦因子关联式(称为KOWALSKI形式公式)。结果表明,BLASIUS方程预测的气壁摩擦因子与实验结果比较吻合;在得到气壁与液壁剪切应力后,通过外推界面附近的雷诺数剪切分布,分别得到了光滑和波动界面的剪切应力,建立了KOWALSKI形式表达的分层流封闭关系。
ANDRITSOS等[14]、HAGIWARA等[31]通过实验分别分析了界面行为(如界面波)对气壁和界面剪切应力的影响,并讨论了气壁和界面摩擦因子的本构关系。ANDRITSOS等[14]利用动量守恒预测了界面剪切应力,同时提出过渡气相表观速度概念,以此作为光滑与波状分层流的界限。结果表明,对于光滑分层流,界面摩擦因子等于气壁摩擦因子;当出现界面波,即气相表观速度大于过渡值,界面与气壁的摩擦因子之比为液高(实际液高/管径)和气相表观速度的本构关系式。HAGIWARA 等[31]用热膜电导探针和热线测定了充分发展的气液两相流的壁面剪切应力、液膜厚度和气体速度,并观察了气壁剪切与界面波的关系。实验结果表明,气液界面上的波幅增大时,气壁剪切应力也随之增大,为界面摩擦因子与气壁摩擦因子之比作为分层流封闭关系提供了合理依据。
TZOTZI等[32]在内径为0.025m的水平管内,以空气、二氧化碳、氦气作为气相,水、丁醇-水溶液作为液相,进行气液两相分层流动实验,并在ANDRITSOS & HANRATTY模型的基础上,着重考虑气体密度、表面张力两个因素,完善从光滑流到2D波、从2D波到大幅度波转型的半理论相关性和两类波状流界面摩擦因子的经验关系式。结果表明,转型相关性与实验数据符合良好。
STRAND[33]的实验在长度为 35m、内径为10cm的水平管道中进行,利用探针测量了空气-水分层流流场分布,得到了气壁、液壁和界面剪切应力,并通过摩擦因子与壁面粗糙度关系[34]计算了分层流界面等效的粗糙度,其结果为许多新的CFD方法提供了数据基础。
LI等[35]用两种方法测定界面剪切应力,对气相采用动量平衡法,对气-液界面采用雷诺剪切应力外推法,得到一种新的预测界面剪切应力公式。结果表明,界面摩擦因子与空隙率和气体表观雷诺数有关,预测结果与实验数据吻合较好。
3 气液两相分层流界面剪切预测数值计算
目前,数值计算方法(CFD)在预测水平管气液界面剪切应力的研究应用已经越来越普遍[36]。DOMINIQUE[37]在讨论气液两相流所有流型的CFD建模的困难时指出,由于气液两相流界面的离散性质,CFD方法受限于空间和时间的精确计算。
较早的应用 CFD研究气液两相分层流的工作主要集中于利用MARKER & CELL或Volume of Fluid(VOF)方法模拟分析2D/3D自由表面流动或气泡的生长。AKAI等[38]提出了局部一维数值分层流两方程湍流模型,预测了气液两相的压力梯度、持液率和速度,与实验数据吻合较好,但未能给出界面波动于气相雷诺数的经验关系式。
SHOHAM等[8]最早用 CFD建立了二维分层湍-湍气液两流体模型,应用涡黏理论求解液相N-S动量方程,用零方程模型计算湍流黏度,在修正界面应力时考虑了界面结构,预测出液相的速度场、压降和持液率,得到了比 LOCKHART & MARTINELLI和TAITEL & DUKLER更好的结果。
ISSA[39]对充分发展的气液两相分层流建立了二维湍流-湍流k-ε两方程模型,采用曲线正交网格和双极坐标系,得到了接近实验数据的气液两相压力梯度、速度场和界面高度。但如何指定气液界面(特别是波状分层流界面)的湍动能和湍动能耗散率边界条件,尚未得到解决。模型中,包括气液界面的所有边界都要使用壁面函数,并需要借助额外的经验公式,且只适用于内径小于或等于25mm的管道。
MEKNASSI等[40]的工作很有代表性,将气液界面处理为具有等效粗糙度的粗糙壁面,壁面函数采用低雷诺数k-ε两方程湍流模型,通过有限差分法成功地模拟了STRAND[33]和LOPEZ[41]的实验。结果表明,当考虑二次流时,模拟结果与实验结果符合良好,气相的模拟结果证实了界面粗糙度能够反映气液界面的相互作用。
NEWTON等[42]通过动量方程改进了50mm和80mm内径气液水平管流KOWALSKI形式的界面摩擦因子关联式,其思路是尽可能少地使用经验关系式,以提高结论的普适性。后来,NEWTON等[43-44]又分别对湍流气液两相和波动气液两相分层流进行了数值模拟。前者气液界面按照光滑处理,湍流模型只引用了单相流阻尼函数一个经验公式,二维轴向动量方程式在气液各相中分别求解,湍流黏度由低雷诺数k-ε模型求得;后者将界面处理为具有等效粗糙度的壁面,除阻尼函数外,还引用了粗糙度与摩擦因子经验关系式,给出了界面剪切应力经验分布函数,由k-ε湍流模型进行求解。
MOUZA等[3]利用CFX软件模拟了VLACHOS等[45]的实验,将气液两相分开进行模拟,并计算了气壁、液壁和气液界面剪切应力分布情况,发现模拟计算结果与实验数据吻合较好。
BERTHELSEN等[46-47]借助 NEWTON等[44]的界面剪切分布函数,二维稳态动量方程采用有限差分格式复合求解,在管壁和气液界面附近使用重叠网格技术进行局部加密,近壁处采用 k-l一方程模型,远离壁面时采用 k-ε两方程模型,并在气液界面处采用 Level-Set界面重构技术对水平管和微倾管分层流进行了数值模拟,讨论了剪切应力值及其分布情况,模拟结果与湍流流动的实验结果吻合较好。
GHORAI等[48]利用FLUENT软件建立VOF模型,模拟了STRAND[33]和LOPEZ[41]的实验,使用STRAND得到的界面等效粗糙度对气液界面进行了修正。采用控制体积有限元法(CVFEM)求解控制方程,CVFEM的优点在于既保留了有限单元法(FEM)网格划分的灵活性,又未牺牲控制容积有限差分法(CVFDM)的鲁棒性和经济性,网格划分采用非结构网格。通过数值计算得到了满意的模拟效果,并分析了气液界面摩擦因子和液壁摩擦因子的本构关系,给出了界面摩擦因子与气壁摩擦因子之比与表观流速的关联式。
DE SAMPAIO等[49]利用有限单元法和k-ω湍流模型对层-层分层流进行了数值模拟,迭代过程中,将液位高度和压降的估计值直接带入控制方程,并用NEWTON-RAPHSON法封闭方程,即不断循环修正液位高度和压降值,直到满足收敛精度。最后将计算的壁面剪切应力、界面剪切应力和液高预测与已有实验进行了对比,认为k-ω湍流模型能很好地模拟高含液率的光滑分层流。
SIDI-ALI等[36]的工作值得关注,利用FLUENT软件,在HANSEN等[8]二维移动壁面模型基础上,建立了三维气相的移动壁面模型,即将气液界面定义为一个无滑移的匀速移动壁面,通过对比STRAND[33]实验的气速分布,模拟得到了移动壁面的移动速度,利用粗糙速度通过有限容积法计算出界面摩擦因子和界面剪切应力。不过他们的模型存在两个明显的缺陷;第一是移动壁面的移动速度是液相速度平均速度,这与实际情况不同;二是他们计算的气壁剪切应力明显大于理论和实验结果(平均误差大于 90%),因此他们并没有进一步讨论气相封闭关系。
4 5种现有模型的压降与持液率预测对比分析
在对气壁、液壁和气液界面剪切应力的预测基础上,封闭气液两相动量方程,从而达到通过已知条件(如管径、气液两相物性值和气液两相表观速度等)实现对持液率和压降的预测,这就是对分层流封闭关系研究的主要意义,也是工程实践最关心的问题。
4.1 气壁摩擦因子关联式
分层流气壁剪切应力的计算基础是单相流气壁剪切应力的计算,早期气液两相流都采用单相流计算方法,由于分相流模型在分层流模型预测中的优势,这里只对两相流的气壁剪切作简单介绍。TAITEL等[6-7]分层流气壁剪切应力由BLASIUS形式公式计算仍然有很高精度,说明分层流气壁剪切与单相流壁面剪切非常相似。表1给出了4个具有代表性的分层流气壁摩擦因子计算公式。
4.2 液壁摩擦因子关联式
BLASIUS公式和TAITEL & DUKLER公式在较低的雷诺数或者光滑分层流下,预测的液壁剪切应力误差不大,但随着雷诺数的增加,上述两个关联式误差较大,不能满足预测精度。KOWALSKI的液壁摩擦因子关联式考虑了持液率关系,被更多研究者所使用。4个湍-湍分层流液壁摩擦因子关联式见表2。

表1 分层流气壁摩擦因子关联式

表2 分层流液壁摩擦因子关联式
4.3 界面摩擦因子关联式
早期TAITEL等认为界面摩擦因子等于气壁摩擦因子,后来的研究发现这一假设只在雷诺数较小的湍流和层流中才能较好地满足实际结果[8,52]。对于界面剪切摩擦因子关联式,大致分以下几种典型形式:
(1)常数,如SHOHAM & TAITEL[8];
(2)BLASIUS形式,如 TAITEL 等[6-7],SIDI-ALI等[36];
(3)KOWALSKI形式,如KOWALSKI[30],NEWTON等[53];
(4)fi/fG经验公式,如ANDRITSOS等[14],TZOTZI等[32]。
表3给出了7个典型的湍-湍分层流界面摩擦因子关联式。TAITEL & DUKLER模型认为气壁摩擦因子等于界面摩擦因子;SHOHAM等[8]沿用了COHEN & HANRATTY矩形管(0.305m×0.0254 m)分层流实验结果,介质为空气和水,在波状分层流下,平均界面摩擦因子为0.0142;KOWALSKI对空气-水和氟利昂12-水系统进行实验测量,管径0.051m,管口压力分别为2.25kPa和4.2kPa,在气壁和液壁的摩擦因子关联式与动力方程的本构关系基础上,提出了KOWALSKI形式的界面摩擦因子关联式;HART等使用ECK[54]单相流壁面剪切应力公式,将气液界面假设为粗糙壁面;CROWLEY等[55]在研究微倾管流型转变时发现,当界面摩擦因子使用5倍或10倍由TAITEL & DUKLER公式计算的气壁摩擦因子时,预测的流型与实验结果能很好地吻合;SIDI-ALI等[36]通过三维移动壁面的CFD模型得到的移动壁面摩擦因子关联式;TZOTZI等以空气、二氧化碳、氦气作为气相,水、丁醇-水溶液作为液相,通过波动理论完善从光滑流到2D波、从2D波到大幅度波的转型。

表3 分层流界面摩擦因子关联式
4.4 不同模型预测结果对比
选择5个具有代表意义的模型进行对比分析,它们是TAITEL & DUKLER[6-7](T-D)、SHOHAM & TAITEL[8](S-T)、KOWALSKI[30](K)、SIDI-ALI & GATIGNOL[36]( SA-G) 和TZOTZI & ANDRITSOS[32](T-A),其中,SA-G模型为半封闭模型,且气壁摩擦因子计算误差很大,没有达到改进T-D公式的目的,而并没有考虑液壁摩擦因子,因此,这里对比计算中,SA-G模型的气壁和液壁摩擦因子采用TAITEL & DUKLER公式;T-A的气壁摩擦因子直接使用TAITEL & DUKLER公式。实验数据取自ANDRITSOS[14](D=0.09525m)、ANDRITSOS[56](D=0.08m)、STRAND[33](D=0.1m)和AYATI[57](D=0.1m)等,介质为空气和水,表观雷诺数范围满足 8000≤ReSG≤90000和 5000≤ReSL≤17000。图2为5种不同模型压降和持液率预测结果与实验结果对比。
从图2(a)可以看出,T-D模型和T-A模型预测的持液率偏大,前者的误差主要来自界面剪切的过小预测,后者的误差来自对液壁剪切的过大预测;K模型预测效果较好,但预测值分布的总体趋势与实验测量结果不吻合,适用范围有限;S-T模型和由T-D壁面摩擦因子关联式封闭的SA-G模型在很大程度上修正了T-D模型的假设造成的误差,这一结果从界面剪切应力计算结果与实验结果吻合得很好可以得到解释。
从图2(b)可以看出,T-D模型和T-A模型预测的压降误差最大,前者的误差主要来自界面剪切的过小预测,后者的误差来自液壁剪切的过大预测,这与持液率预测结果相对应;S-T模型预测的压降误差较小,说明fi=0.0142在所讨论的雷诺数流动中能保证预测结果误差在20%以内,但由T-D壁面摩擦因子关联式封闭的SA-G模型误差却很大,这与SA-G界面摩擦因子预测公式在较大雷诺数下预测值明显偏低有关;K模型预测效果很好,可见基于KOWALSKI形式的封闭关联式在压降预测方面具有较高精度。
5 结语与展望
(1)理论模型、实验测量、CFD数值计算 3类不同研究方法都可以较好地预测分层流界面剪切性质,进而预测分层流的持液率和压降。其中理论模型为实验和CFD方法提供了理论依据,实验结果验证并修正了理论模型,而CFD数值计算可以通过合理假设,在较少引入已有本构关联式的前提下预测分层流,并提供更详细的流场细节。但3类研究方法都具有一定的局限性,理论模型受限于模型的简化条件和方程的封闭性,实验间接测量受限于实验测量技术与数据分析,CFD则受限于计算技术和方法。
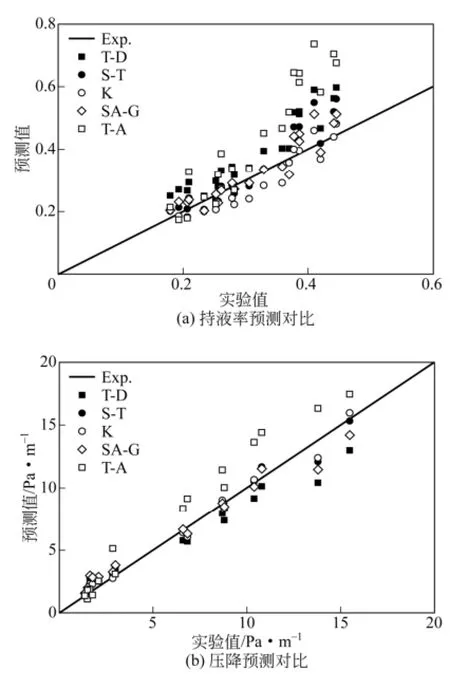
图2 5种模型预测结果与实验结果对比
(2)理论模型取得了一定的成果,并在实验和CFD仿真计算中起到了关键的指导作用。然而理论模型受到两方面限制:一是理论模型的简化假设条件,这些简化导致在实际应用中适用范围较窄;二是理论模型的封闭性。对于绝大多数的理论模型,都需要额外提供本构关系式来封闭求解方程,这些本构关系通常是基于实验的经验关系式。如何建立合理的分层流理论模型,是分层流界面剪切预测的关键。应根据工程普遍问题提出合理假设,并针对界面建立更精确的局部模型,使模型预测具有更大的适应性和准确性;同时大力开展有效的实验工作,得到更好的符合实际问题的经验关系式,使理论模型的求解更接近实际情况。
(3)由于实验条件在很大程度上影响了气液两相分层流界面剪切预测的结论,因此很有必要在实验过程中考虑更多的影响因素,但这样也会使研究难度无形加大。此外,实验室中的大部分实验与实际工况环境相差较大,因而会产生实验数据与实际工况不同程度的误差。因此,如何在实验室中得到与实际工况(特别是高温高压等特殊工况)相符的研究结论,仍需要做更多的基础工作。
(4)分层流流场细节和界面行为直接影响理论模型建立和CFD数值计算结果的正确性。应完善更加细致的分层流流场细节和界面行为的实验观察,特别是对界面波动与气泡/液滴的观察,为理论模型的合理建立和 CFD数值计算的正确求解提供更详细的科学数据。
(5)CFD数值计算仿真技术可以考虑被理论模型简化的条件,也可以观测到实验难以观测的流程细节特征。但是,CFD模型的建立离不开理论和实验得到的已知结论,并且,计算技术直接影响到计算结果,对于界面行为的模拟一直是CFD研究的难点和重点。随着CFD技术和方法的不断发展,在更精确的流场特征前提下,气液两相分层流界面行为模拟和界面剪切应力的预测是未来 CFD数值计算最主要的挑战,也是大势所趋。
参 考 文 献
[1] ULLMANN A,BRAUNER N. Closure relations for two-fluid models for two-phase stratified smooth and stratified wavy flows[J]. International Journal of Multiphase Flow,2006,32(1):82-105.
[2] 郭烈锦. 两相与多相流动力学[M]. 西安:西安交通大学出版社,2002.
[3] MOUZA A A,PARAS S V,KARABELAS A J. CFD code application to wavy stratified gas-liquid flow[J]. Chemical Engineering Research and Design,2001,79(5):561-568.
[4] LINÉ A,LOPEZ D. Two-fluid model of wavy separated two-phase flow[J]. International Journal of Multiphase Flow,1997,23(6): 1131-1146.
[5] LOCKHART R W,MARTINELLI R C. Proposed correlation of data for isothermal two phase,two component flow in pipes[J]. Chemical Engineering Progress,1949,45(1):38-48
[6] TAITEL Y,DUKLER A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal,1976,22(1):47-55.
[7] TAITEL Y,DUKLER A E. A theoretical approach to the Lockhart-Martinelli correlation for stratified flow[J]. International Journal of Multiphase Flow,1976,2(4):591-595.
[8] SHOHAM O,TAITEL Y. Stratified turbulent-turbulent gas-liquid flow in horizontal and inclined pipes[J]. AlChE Journal,1984,303 (3):377-385.
[9] HANSEN E A,VESTED H J. Liquid hold-up,pressure drop,and velocity profiles in steady uniform stratified flow[J]. Journal of Energy Resources Technology,1991,113(2):87-93.
[10] ULLMANN A,ZAMIR M,GAT S,et al. Multi-holdups in co-current stratified flow in inclined tubes[J]. International Journal of Multiphase Flow,2003,29(10):1565-1581.
[11] ULLMANN A,GOLDSTEIN A,ZAMIR M,et al. Closure relations for the shear stresses in two-fluid models for laminar stratified flow[J]. International Journal of Multiphase Flow,2004,30(7/8):877-900.
[12] KANG H C,KIM M H. The relation between the interfacial shear stress and the wave motion in a stratified flow[J]. International Journal of Multiphase Flow,1993,19(1):35- 49.
[13] 刘夷平,王茹金,陈超,等.气液两相分层流剪切应力的不确定度分析[J]. 实验流体力学,2012,26(4):43-47.
[14] ANDRITSOS N,HANRATTY T J. Influence of interfacial waves in stratified gas-liquid flows[J]. International Journal of Multiphase Flow,1987,13(5):583-603.
[15] HART J,HAMERSMA P J,FORTUIN J M H. Correlations predicting frictional pressure drop and liquid holdup during horizontal gas-liquid pipe flow with a small liquid holdup[J]. International Journal of Multiphase Flow,1989,15(6):947-964.
[16] CHEN X T,CAI X D,BRILL J P. Gas-liquid stratified-wavy flow in horizontal pipelines[J]. Journal of Energy Resources Technology,1997,119:209-216.
[17] VLACHOS N A,PARAS S V,KARABELAS A J. Prediction of holdup,axial pressure gradient and wall shear stress in wavy stratified and stratified/atomization gas/liquid flow[J]. International Journal of Multiphase Flow,1999,25(2):365-376.
[18] VLACHOS N A. Studies of stratified/atomization two-phase flow in a horizontal pipe[D]. Thessaloniki:Aristotle University of Thessaloniki,1997
[19] NG T S,LAWRENCE C J,HEWITT G F. Interface shapes for two-phase laminar stratified flow in a circular pipe[J]. International Journal of Multiphase Flow,2000,27(7):1301-1311.
[20] BRAUNER N,ROVINSKY J,MOALEM M D. Determination of the interface curvature in stratified two-phase systems by energy considerations[J]. International Journal of Multiphase Flow,1996,22(6):1167-1185.
[21] BRAUNER N,ROVINSKY J,MOALEM M D. Analytical solution for Laminar-Laminar two-phase flow in circular conduits[J]. Chemical Engineering Communication,1996,141/142(1):103-143.
[22] BRAUNER N,ROVINSKY J,MOALEM M D. Analytical solution of laminar stratified flow with curved interfaces[C]// Proceedings of the NURETH-7 Meeting,ANS 1,1995:192-211.
[23] BRAUNER N,ROVINSKY J,MOALEM M D. Characteristics of annular and stratified two-phase flow in the limit of fully eccentric core annular configuration[C]// Proc. of the ExHFT 4,Brussels,1997.
[24] BRAUNER N,MOALEM M D,ROVINSKY J. A two-fluid model for stratified flows with curved interfaces[J]. International Journal of Multiphase Flow,1998,24(6):975-1004.
[25] ROVINSKY J,BRAUNER N,MOALEM M D. Analytical solution for laminar two-phase flow in a fully eccentric core-annular configuration[J]. International Journal of Multiphase Flow,1997,23 (3):523-543.
[26] SOLEIMANI A. Phase distribution and associated phenomena in oil-water flows in horizontal tubes[D]. London:Imperial College,University of London,1999.
[27] BIRVALSKI M,TUMMERS M J,DELFOS R,et al. PIV measurements of waves and turbulence in stratified horizontal two-phase pipe flow[J]. International Journal of Multiphase Flow,2014,62:161-173.
[28] FULLMER W D,RANSOM V H,LOPEZ de Bertodano M A. Linear and nonlinear analysis of an unstable, but well-posed,one-dimensional two-fluid model for two-phase flow based on the inviscid Kelvin-Helmholtz instability[J]. Nuclear Engineering and Design,2014,268:173-184.
[29] LIU G,WANG Y S,ZANG G J,et al. Viscous Kelvin- Helmholtz instability analysis of liquid-vapor two-phase stratified flow for condensation in horizontal tubes[J]. International Journal of Heat and Mass Transfer,2015,84:592-599.
[30] KOWALSKI J E. Wall and interfacial shear stress in stratified flow in a horizontal pipe[J]. AIChE Journal,1987,32(2):274-281.
[31] HAGIWARA Y,ESMAEILZADEH E,TSUTSUI H,et al. Simultaneous measurements of liquid film thickness,wall shear stress and gas flow turbulence of horizontal wavy two-phase flow [J]. International Journal of Multiphase Flow,1989,15(3):421- 431.
[32] TZOTZI C,ANDRITSOS N. Interfacial shear stress in wavy stratifed gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow,2013,54:43-54.
[33] STRAND Ø. An experimental investigation of stratified two-phase flow in horizontal pipes[D]. Oslo:University of Oslo,1993.
[34] HAALAND S E. Simple and explicit formulas for the friction factor in turbulent pipe flow[J]. Journal of Fluids Engineering,1983,105: 89-90.
[35] LI W D,SUN K X,ZHOU F D. Interfacial shear stress of stratified flow in a horizontal pipe[J]. Chinese Journal of Chemical Engineering,1999,7(3):263-270.
[36] SIDI-ALI K,GATIGNOL R. Interfacial friction factor determination using CFD simulations in a horizontal stratified two-phase flow[J]. Chemical Engineering Science,2010,65(18):5160- 5169.
[37] DOMINIQUE B. The difficult challenge of a two-phase CFD modelling for all flow regimes[J]. Nuclear Engineering and Design,2014,279:116-125.
[38] AKAI M,INOUE A,AOKI S. The prediction of stratified two-phase flow with a two equation model of turbulence[J]. International Journal of Multiphase Flow,1981,7(1):21-39.
[39] ISSA R I. Prediction of turbulent,stratified,two-phase flow in inclined pipes and channels[J]. International Journal of Multiphase Flow,1988,14(2):141-154.
[40] MEKNASSI F,BENKIRANE R,LINÉ A,et al. Numerical modelling of wavy stratified two-phase flow in pipes[J]. Chemical Engineering Science,2000,55(20):4681-4697.
[41] LOPEZ D. Ecoulements diphasiques a phases separees a faible contenu de liquide[D]. France:I.N.P. Toulouse,1994.
[42] NEWTON C H,BEHNIA M. On the use of the stratified momentum balance for the deduction of shear stress in horizontal gas-liquid pipe flow[J]. International Journal of Multiphase Flow,1998,24(8): 1407-1423.
[43] NEWTON C H,BEHNIA M. Numerical calculation of turbulent stratified-gas-liquid pipe flows[J]. International Journal of Multiphase Flow,2000,26(2):327-337.
[44] NEWTON C H,BEHNIA M. A numerical model of stratified-wavy gas-liquid pipe flow[J].Chemical Engineering Science,2001,56 (24):6851-6861.
[45] VLACHOS N A,PARAS S V,KARABELAS A J. Liquid-to-wall shear stress distribution in stratified/atomization flow[J]. International Journal of Multiphase Flow,1997,23(5):845-863.
[46] BERTHELSEN P A,YTREHUS T. Calculations of stratified wavy two-phase flow in pipes[J]. International Journal of Multiphase Flow,2005,31(5):571-592.
[47] BERTHELSEN P A,YTREHUS T. Stratified smooth two-phase flowusing the immersed interface method[J]. Computers & Fluids,2007,36(7):1273-1289.
[48] GHORAI S,NIGAM K D P. CFD modelling of flow profiles and interfacial phenomena in two-phase flow in pipes[J]. Chemical Engineering and Processing,2006,45(1):55-65.
[49] DE SAMPAIO P A B,FACCINI J L H,SU Jian. Modelling of stratified gas-liquid two-phase flow in horizontal circular pipes[J]. International Journal of Heat and Mass Transfer,2008,51: 2752-2761.
[50] HAND N P. Gas-liquid co-current flow in a horizontal pipeline[D]. Belfast:The Queen's University of Belfast,1991.
[51] SRICHAI S. High pressure separated two-phase flow[D]. London: Imperial College,1994.
[52] BARNEA D,TAITEL Y. Structural and interfacial stability of multiple solutions for stratified flow[J]. International Journal of Multiphase Flow,1992,18(6):821-830.
[53] NEWTON C H,BEHNIA M. On the use of the stratified momentum balance for the deduction of shear stress in horizontal gas-liquid pipe flow[J]. International Journal of Multiphase Flow,1998,24(8): 1407-1423.
[54] ECK B. Technische Stromunglehre[M]. New York:Springer,1973.
[55] CROWLEY C J,WALLIS G B,BARRY J J. Validation of a one-dimensional wave model for the stratified-to-slug flow regime transition,with consequences for wave growth and slug frequency[J]. International Journal of Multiphase Flow,1992,18(2):249-271.
[56] ANDRITSOS N. Statistical analysis of waves in horizontal stratified gas-liquid flow[J]. International Journal of Multiphase Flow,1992,18(3):465-473.
[57] AYATI A J,KOLAAS A,JENSEN G W,et al. A PIV investigation of stratified gas-liquid flow in a horizontal pipe[J]. International Journal of Multiphase Flow,2014,61:129- 143.
Progress of interfacial shear stress in the gas-liquid stratified flow in horizontal pipes
ZHENG Ping,ZHAO Liang
(College of Petroleum Engineering,Liaoning Shihua University,Fushun 113001,Liaoning,China)
Abstract:The gas-liquid two-phase stratified flow has complex momentum and energy transmission phenomena at interface,although its pattern is simple. There are still no unified conclusions for interfacial shear stress in stratified flow. Current progress of interfacial shear stress in horizontal pipes were elaborated by theoretical models,experimental models and numerical simulations. As for theoretical models,closure models were established by models simplification and empirical correlations. Empirical correlations were corrected with closure relations in experiments. Due to simplifying assumptions and experimental conditions,there are some limitations in predicting the interfacial shear stress with theoretical and experimental ways. The detailed flow fields were studied by numerical simulations,but closure relations have been less obtained so far. Five existing models are compared according to liquid holdup and pressure drop. The future research trends of gas-liquid two-phase stratified flow interfacial shear stress in horizontal pipes were further discussed. More detailed local models are needed to be proposed and engineering practice should be taken into account. It is necessary to develop new methods of gas-liquid interface calculations and closure relations for numerical simulations.
Key words:horizontal pipe;gas-liquid flow;stratified flow;interfacial shear stress;liquid holdup;pressure drop
中图分类号:O 359.1
文献标志码:A
文章编号:1000-6613(2016)05-1289-09
DOI:10.16085/j.issn.1000-6613.2016.05.004
收稿日期:2015-11-09;修改稿日期:2016-02-01。
基金项目:国家自然科学基金项目(51201009)。

