以“教给解题策略”为重点的问题解决教学

四川省雅安市汉源县九襄镇第四小学 郝淑敏

《新课程标准》指出：让学生形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力和创新精神。为了实现《新课程标准》的这一精神，在小学数学教学中，我们必须重视“问题解决”的教学，从小培养小学生灵活运用所学的数学知识去解决他们面对的有关问题，是当前小学数学教育的一个显著特点，是小学数学教育面临的一项重要任务。

在教学中，教师应尊重每一个学生的个性特征，允许并鼓励学生从不同角度去认识问题，分析问题，采用不同的方式表达自己的想法，用不同的知识与方法解决问题，并进行解法优化，从中找出简捷的解法。鼓励解决问题策略的多样化，是因材施教、促进每一个学生充分发展的有效途径。

以下就下例的教学实践作一下介绍：

工程队修补一条公路，公路总长12千米，前3天修补了1.5千米。照这样计算，修补完这条公路还需要多少天？

一、教师引导学生从条件入手进行分析

可找出：“先求出每天修路长度，再求出修补完这条公路的天数，再减去已修路的天数，即可求得修补完这条公路的天数。” 从而得到：

答：修补完这条公路还需要21天。

二、教师引导学生从问题入手进行分析

就会发现：“要求得修补完这条公路还要多少天，必须知道还剩下多少千米未修和平均每天修补多少千米。”根据题目中所给条件，从而得到：

答：修补完这条公路还需要21天。

三、教师进一步引导学生进行分析

就能找到还可以用：“先求出已修补公路长的千米数占全路长的千米数的几分之几，再求得修补完这条公路所需的总天数，再减去已修天数，就可以求得修补完这条公路还需要的天数。”从而得到：

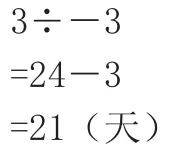
答：修补完这条公路还需要21天。

四、教师引导学生抓住这类应用题的关键词语入手分析

学生也能明白：“‘照这样计算’就是说每天修补公路的千米数（即工作效率）是一定的，所以需要修补公路的千米数（即工作总量）和修补公路的天数（即工作时间）成正比例关系。”从而得到：

1.解：设修补完这条公路还要X天。

2.解：设修补完这条公路共要X天。

答：修补完这条公路还需要21天。

五、教师引导学生用代数知识列方程来解答问题

则可以运用以下的等量关系列出方程求解：“平均每天修路的长度×修路的天数=公路总长度”“修路的总天数－还需要的天数=已修的天数”“已修路的天数+还要修路的天数=修路的总天数。”从而得到：

解：设修补完这条公路共要X天。

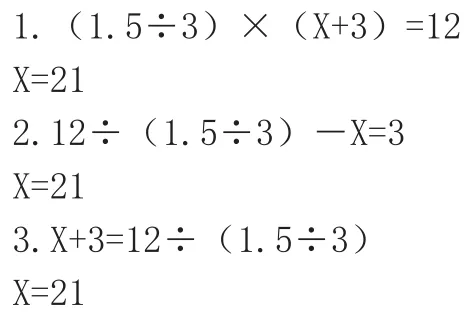
答：修补完这条公路还需要21天。

六、具有“照这样计算”特征的应用题，我们还可以运用倍比法去解答

1.求得公路总长度是已修公路长度的几倍，那么修路的总天数就是已修路天数的几倍，再减去已修路天数就得还需修路的天数。从而得：

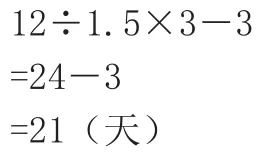
答：修补完这条公路还需要21天。

2.求得未修的公路长度是已修公路长度的几倍，那么还需修路天数就是已修路天数的几倍。从而得到：

答：修补完这条公路还需要21天。

在教学中教师能不失时机地对学生进行运用所学知识尝试用多种方法解题的强化训练，学生思维的敏捷性和灵活性就会提高，从不同角度去分析问题，合理、灵活解决问题的能力就会不断增强。