广西南宁巨尾桉DH32—28植苗林调查因子关系模型研究

黄平升　唐小诚　廖克波　杨紫龙　李婷

摘要[目的]调查广西南宁巨尾桉（DH32-28）植苗林各调查因子间的关系。[方法]对在广西南宁树木园新塘和横县林区内生长正常的巨尾桉（DH32-28）植苗林进行调查，分别测定每株树的胸径、树高、年龄等树木调查因子，并对其相关性进行分析，建立胸径与造林时间、树高与造林时间、胸径与树高等因子之间的一系列数学模型，并进行模型的实用性和精度检验。[结果]胸径、树高与造林时间的对数函数关系比较密切，树高与胸径的二次函数模型关系比较密切。胸径与造林时间的关系可以用对数函数模型y=-3.310+4.132 lnx来反映，树高与造林时间的关系可以用对数函数模型y=-15.881+8.816lnx来反映，胸径与树高的关系可以用二次函数模型y=0.635+0.822x+0.042x2来反映。[结论]模型揭示了广西南宁巨尾桉（DH32-28）植苗林各调查因子之间的生长规律性，同时还可以用于桉树人工林林分生长预估中单株树木潜在的生长分析，对桉树人工林的可持续经营利用和森林生态系统恢复具有一定的指导意义。

关键词 巨尾桉（DH32-28）；人工林；调查因子；关系模型；南宁

中图分类号 S792.39 文献标识码 A 文章编号 0517-6611（2016）05-185-04

Abstract [Objective]To investigate the relationship between survey factors of Eucalyptus （DH3228） forest planting in Nanning City of Guangxi Zhuang Autonomous Region.[Method]In Xintang and Hengxian Forest Regions of Nanning Arboretum， normal Eucalyptus （DH3228） forest planting was investigated. Survey factors were detected， such as diameter at breast height ， plant height and plant age. By fully considering the interaction between survey factors， correlation analysis was carried out. A series of mathematical model were carried out， including diameter at breast height and afforestation time， plant height and afforestation time， diameter at breast height and plant height. Practicability and accuracy test of model were detected.[Result]The logarithmic function relationships among diameter at breast height， plant height and afforestation time were relatively close， as well as the quadratic function model relation between plant height and diameter at breast height. Relationship between diameter at breast height and afforestation time could be reflected by logarithmic function model y= -3.310 + 4.132lnx； relationship between plant height and afforestation time could be reflected by logarithmic function model y= -15.881 + 8.816 lnx； relationship between diameter at breast height and plant height could be reflected by quadratic function model y=0.635 + 0.822x+ 0.042x2.[Conclusion]The model reveals the growth regularity among survey factors of Eucalyptus （DH3228） forest planting in Nanning City， can be used as the potential growth analysis of single plant in stand growth forecast of survey factors of Eucalyptus plantations， and has certain guiding significance for the sustainable management and ecosystem restoration of Eucalyptus plantations.

Key words Eucalyptus （DH3228）； Plantation； Survey factors； Relation model； Nanning

桉树（Eucalyptus）是桃金娘科（Mgrtaceae）桉属（Eucalyptus）植物的统称，天然分布于澳大利亚及华莱士线以东岛屿，种类包括变种和亚种有近1 000种之多，是世界四大速生树种之一。因其具有速生、丰产、用途广、适用性强、经济效益高等特点而成为重要的人工用材造林树种之一，在世界各地广泛种植。20世纪中后期，随着林纸一体化和林板一体化的发展，在热带和亚热带地区，桉树人工林得到了迅速的发展[1]。广西引种桉树有近百年历史，20世纪70年代先后从国外引入160 多个种源，普遍推广栽培的有窿缘桉（E. exserta）、细叶桉（E. tereticornis）、赤桉 （E. camaldulensis）（变种）等10多种。

目前，国内外对桉树人工林林分生长模型的研究并不多，均是利用传统方法探索胸径、树高、蓄积、林分密度、立地质量等之间的关系，建立相应的生长模型。曾伟生等[2]利用156块人工林样地，建立了海南省松类、桉类、木麻黄、相思、橡胶5个主要树种（组）的相对树高曲线模型。陈文友[3]调查测定了巨桉1 a中的树高、直径生长以确定最佳的施肥时间。黄从德等[4]运用Weibull分布、反Weibull分布、Logistic方程3种模型拟合了巨桉短周期工业原料人工林林分直径分布规律，结果表明Logistic方程拟合巨桉人工林的直径分布效果较好，并在此基础上分3个立地等级建立了巨桉直径分布收获模型。梁理勇等[5]对雷州林业局2002年森林二类调查的刚果12号桉W5无性系林分279块样地材料，进行了蓄积量与胸径、树高、密度及其之间关系的探讨分析。周元满等[6]以Logistic累计分布曲线方程为模型，从Logistic模型的生物学意义出发，对桉树人工林的现实最大生产潜力进行了研究，以探求最大生产潜力的计算方法，确定最佳生产力的时期。而针对广西南宁巨尾桉（DH32-28）植苗林诸调查因子之间相关性的研究报道较为少见。为此，笔者对广西南宁2010～2014年营造的巨尾桉（DH32-28）植苗林进行了调查，通过建立数学模型研究

桉树人工林植苗林样木胸径、年龄、树高等调查因子之间的关系，分析巨尾桉（DH32-28）植苗林的生长趋势，为巨尾桉（DH32-28）植苗林林分结构调整、森林经营措施制定等提供理论参考，以期促进广西南宁巨尾桉（DH32-28）植苗林的可持续经营。

1 材料与方法

1.1 研究区自然概况

试验地位于广西南宁树木园横县、新塘造林部，地处106°33′～109°36′E，21°36′～24°02′N。属南亚热带季风气候，光热资源充足，湿润多雨，年均气温20.3～22.4 ℃，年平均降雨量815～1 686 mm，年平均日照时数1 275～1 579 h。试验地为丘陵山区，最高海拔为400 m，最低为150 m，土壤为砖红性红壤。

1.2 研究方法

选择造林密度为1 425株/hm2的巨尾桉（DH32-28）植苗林林地进行调查。结合造林资料，确定造林月份。选取1、2、3、4、5年生林分中生长平均的林分作为调查固定样地，每个样地20 m×30 m，共计120个样地，对每个样地内桉树进行每木检尺。调查数据采用Excel进行整理和计算，对外业调查数据进行规范化整理，计算平均树高和胸径生长量，用SPSS 17.0 绘制散点图。将收集到的数据随机分为2组，1组用于建立数学模型，另1组用于模型实用性检验。在对测定因子的相关性进行散点图形分析的基础上，分别选用幂函数、对数函数、二次函数、三次函数等对测定因子之间的关系进行拟合，通过决定指数和方差分析，选择最优的函数关系模型建立经验方程，最后对模型的实用性进行检验。

2 结果与分析

2.1 胸径与造林时间

2.1.1 数据散点图。

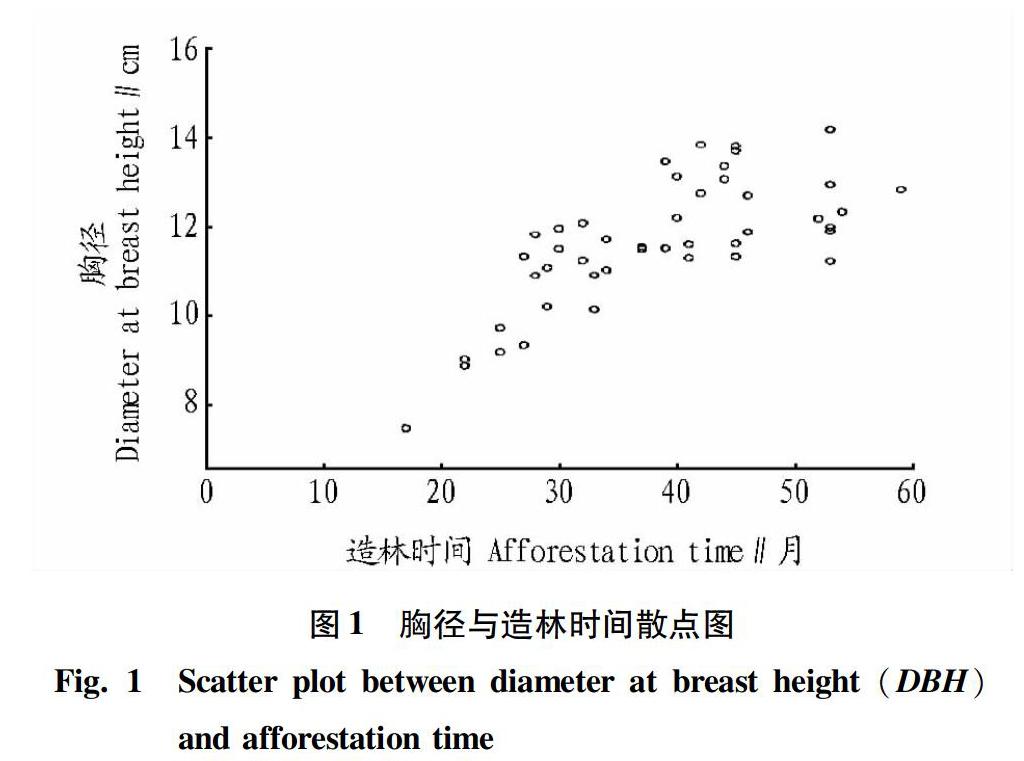
将野外调查收集的巨尾桉（DH32-28）植苗林每个林分的胸径和造林时间实测值绘制散点图，结果见图1。

由图1可知，巨尾桉（DH32-28）植苗林随着造林时间的增加，胸径变化幅度逐渐增加，反映出所收集的数据充分体现了不同立地条件下树木的生长状况。2个测定因子造林时间与胸径之间具有一定的相关性，呈一定的曲线或线性关系，可进行曲线或线性方程的拟合。

2.1.2 相关模型选择与建立。

根据上述分析，初步选择符合2个测定因子相关性趋势的函数模型，用SPSS软件进行回归分析，具体模型及参数值计算结果见表1，拟合结果图见图2。

由表1可知，对数函数曲线模型的R2值最大，为0.752，其次是S函数曲线模型的R2值，为0.751，最小为Logistic函数曲线模型的R2值，为0.563，说明胸径与造林时间的对数函数关系比较密切。

各模型的显著性概率值均小于0.001，因而均有显著性意义。其中F值最大的是对数函数模型，F=185.274。

通过以上判断可初步选定广西南宁巨尾桉（DH32-28）植苗林的胸径—造林时间关系的最佳模型为对数函数模型。采用林分每木实测数据建立的数学模型为y=-3.310+4.132lnx，其中y为胸径，x为造林时间。

2.1.3 回归模型实用性检验。

为进一步确定模型的精度和代表性，将相应的值带入回归模型，计算胸径估计值，将胸径实测值与估计值进行比较，计算相对误差，结果见表2。实用性精度检验结果显示该胸径—造林时间对数函数曲线模型的平均相对误差为3.25%，说明对数函数模型：y=-3.310+4.132lnx可以作为经验方程用于描述胸径—造林时间的关系。

2.2 树高与造林时间

2.2.1 数据散点图。将野外调查收集的巨尾桉（DH32-28）植苗林每个林分的树高和造林时间实测值绘制散点图，结果见图3。

由图2可知，随着造林时间的增加，树高变化幅度逐渐增加，反映出所收集的数据充分体现了不同立地条件下树木的生长状况。2个测定因子造林时间与树高之间具有一定的相关性，呈一定的曲线或线性关系，可进行曲线或线性方程的拟合。

2.2.2 相关模型选择与建立。

根据上述分析，初步选择符合2个测定因子相关性趋势的函数模型，用SPSS软件进行回归分析，具体模型及参数值计算结果见表3，拟合结果图见图4。

由表3可知，对数函数曲线模型的R2值最大，为0.915，其次是S函数曲线模型的R2值为0.856，最小为Logistic函数曲线模型的R2值=0.717，说明树高与造林时间的对数函数关系比较密切。 各模型的显著性概率值均小于0.001，因而均有显著性意义。其中F值最大的是对数函数模型，F=198.850。

通过以上判断可初步选定广西南宁巨尾桉（DH32-28）植苗林的树高—造林时间关系的最佳模型为对数函数模型。采用林分每木实测数据建立的数学模型为y=-15.881+8.816lnx，其中y为树高，x为造林时间。

2.2.3 回归模型实用性检验。

为进一步确定模型的精度和代表性，将相应的值带入回归模型，计算树高估计值，将树高实测值与估计值进行比较，计算相对误差，结果见表4。实用性精度检验结果显示树高—造林时间对数函数曲线模型的平均相对误差为3.13%，说明对数函数曲线模型y=-15.881+8.816lnx可以作为经验方程用于描述树高—造林时间的关系。

2.3 树高与胸径

2.3.1 数据散点图。

将野外调查收集的巨尾桉（DH32-28）植苗林每个林分的树高和胸径实测值绘制散点图，结果见图5。

由图5可知，随着胸径的增加，树高变化幅度逐渐增加，反映出所收集的数据充分体现了不同立地条件下树木的生长状况。2个测定因子胸径与树高之间具有一定的相关性，呈一定的曲线或线性关系，可进行曲线或线性方程的拟合。

2.3.2 相关模型选择与建立。

根据上述分析，初步选择符合2个测定因子相关性趋势的函数模型，用SPSS软件进行回归分析，具体模型及参数值计算结果见表5，拟合结果图见图6。

由表5可知，二次、三次函数曲线模型的R2值最大，为0.962，最小为Logistic函数曲线模型的R2值，为0.790，说明树高与胸径的二次、三次函数关系比较密切。各模型的显著性概率值均小于0.001，因而均有显著性意义。其中F值最大的是二次函数模型，F=630.703。

通过以上判断可初步选定广西南宁巨尾桉（DH32-28）植苗林的树高—胸径关系的最佳模型为二次函数模型。采用林分每木实测数据建立的数学模型为y=0.635+0.822x+0.042x2，其中y为树高，x为胸径。

2.3.3 回归模型实用性检验。

为进一步确定模型的精度和代表性，将相应的值带入回归模型，计算树高估计值，将树高实测值与估计值进行比较，计算相对误差，结果见表6。实用性精度检验结果显示该树高—胸径二次函数曲线模型的平均相对误差为3.25%，说明二次函数曲线模型y=0.635+0.822x+0.042x2可以作为经验方程用于描述树高—胸径的关系。

3 结论与讨论

（1）广西南宁巨尾桉（DH32-28）植苗林的胸径与造林时间之间存在着密切的关系。通过对不同大小的巨尾桉（DH32-28）植苗林的调查数据进行模拟，得出胸径与造林时间的关系可以用对数函数模型y=-3.310+4.132 lnx来反映。 所以在林业调查中，如果知道具体的造林时间，可以用对数函数模型推算胸径。

（2）广西南宁巨尾桉（DH32-28）植苗林的树高与造林时间之间存在着密切的关系。通过对不同大小的巨尾桉（DH32-28）植苗林的调查数据进行模拟，得出树高与造林时间的关系可以用对数函数模型y=-15.881+8.816 lnx来反映。 所以在林业调查中，如果知道具体的造林时间，可以用对数函数模型推算树高。

（3）广西南宁巨尾桉（DH32-28）植苗林的胸径与树高之间存在着密切的关系。通过对不同大小的巨尾桉（DH32-28）植苗林的调查数据进行模拟，得出胸径与树高的关系可以用二次函数模型y=0.635+0.822x+0.042x2来反映。 所以在林业调查中，可用胸径推算树高。

该试验所测数据的林分较小，仅有5 a，故模型只能应用于短期的生长预测。模型的预测结果还有待于今后在实践中检验、修正和进一步完善。

参考文献

[1]谢直兴，严代碧.桉树人工林现状及其可持续发展[J].四川林业科技，2006，7（1）：75-81.

[2]曾伟生，骆期邦，贺东北，等.海南省主要树种相对树高曲线模型应用研究[J].中南林业调查规划，1999，18（2）：1-7.

[3]陈文友.巨桉人工林树高直径年生长分析研究[J].四川林业科技，2001，22（1）：74-76.

[4]黄从德，胡庭兴，赖家明. 四川巨桉短周期工业原料人工林直径分布规律及其收获模型的研究[J].四川林业科技，2003，24（3）：25-30.

[5]梁理勇.雷州刚果12号桉W5无性系林分蓄积量与胸径树高密度及其之间关系的探讨[J].广东林业科技，2004，20（3）：25-27.

[6]周元满，谢正生，刘素青，等.Logistic模型在桉树生长过程估计中的应用[J].南京林业大学学报，2004，28（6）：107-110.