数学思想在高中化学解题中的应用

熊蕾

新课程标准中，课程目标明确要求重视化学与其他学科之间的联系，能综合运用有关的知识、技能与方法分析和解决一些化学问题。作为理科的化学和数学有着密切的联系，若巧妙利用数学思想来解决一些化学问题，会轻松很多。

一、数列

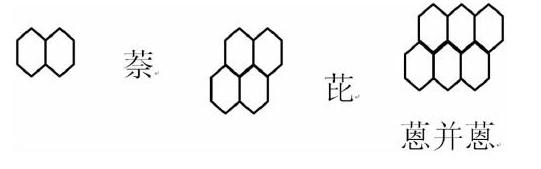
例1：沥青中存在一系列稠环芳香烃

（1）这一系列稠环芳香烃的通式为。

（2）从萘开始，这一系列稠环芳香烃中第25个的分子式为。

（3）随着n值的增大，这一系列稠环芳香烃的含碳量增加，含量以为极限。

解析：（1）首先确定以上三个物质的分子式：C10H8、C16H10、C22H12，再利用数学中等差数列知识：an=a1+（n-1）d，碳原子数an=10+6（n-1）=6n+4，氢原子数an=8+2（n-1）=2n+6，因此，这一系列稠环芳香烃的通式为：C6n+4H2n+6（n>1）。

（2）第25个稠环芳香烃的分子式为：C6×25+4H2×25+6即C154H56。

（3）利用函数法求12（6n+4）/[12（6n+4）+（2n+6）]的最大值（见下文例5）。

二、不等式

不等式法关键是根据题意，挖掘隐含条件，列出不等式。

例2：某CO、C2H4、O2混合气体，平均摩尔质量为30.4，点燃，充分反应后，混合气体中不再有CO、C2H4，试求原混合气体中各气体的体积分数范围（在同温同压下测定）。

解析：首先用“十字交叉法”求出CO、C2H4混合组分与O2的体积比为2 ∶ 3，则原混合气体中ω（O2）=60%；接着，建立不等式求出CO、C2H4的体积分数范围。

设原混合气体5L，则V（O2）=3L，设V（CO）=xL，V（C2H4）=（2-x）L。

x/2+3（2-x）≤3（O2过量），解得1.2L≤x。

又2-x>0，所以1.2L≤x<2L。

即：24%≤ω（CO）<40%，0<ω（C2H4）≤16%。

三、欧拉定律

不同的晶体具有不同的空间结构，多面体的顶点数、面数、棱边数遵循欧拉定律，即顶点数+面数-棱边数=2。

例3：晶体硼的基本结构单元是由硼原子组成的正二十面体的原子晶体，每个面为等边三角形，每个顶点有一个硼原子，请问：这个基本结构单元由个硼原子组成。

解析：根据欧拉定律，列式：硼原子数+20-20×3÷2=2。

即解得硼原子数为12。

四、极值法

例4：已知相对原子质量：Li：6.9，Na：23，K：39，Rb：85。今有某碱金属R及其氧化物R2O组成的混合物10.8g，加足量水充分反应后，溶液经蒸发和干燥得固体16g，据此可金属R是（ ）

A. Li B. Na C. K D. Rb

解析：设此碱金属的相对原子质量为M，依题意：10.8g混合物由R和R2O组成，采用极端假设法。

假设全是R，则生成的ROH为：10.8g/Mg·mol-1=16g/（M+17）g·mol-1，解得M=35.3。

假设全是R2O，则生成的ROH为：2×10.8g/（2M+16）g·mol-1=16g/（M+17）g·mol-1，解得M=10.7。但10.8g为R和R2O的混合物，所以10.7

五、函数

根据题目涉及的化学反应方程式，建立量的函数表达式解题。

例5：例1第（3）小题，求（6n+4）/[12（6n+4）+（2n+6）]的最大值。

解析：f（n）=12（6n+4）/[12（6n+4）+（2n+6）]=（72n+48）/（74n+64）

当n值为∞时，f（n）有最大值，f（n）max=72/74=97.3%。

六、分析推理

有些计算型选择题看上去数据多、计算繁琐，但可能不需计算，直接利用化学原理进行分析、推理就可解出。关键是认真审题、分析，理清思路，抓住原理，附加简单计算，即可得出正确答案。

例6：锌粉、铝粉、镁粉的混合物44g与一定量质量分数为17.25%的硫酸溶液恰好完全反应，将溶液蒸干，得无水固体140g，则放出的气体在标况下的体积为（ ）

A. 22.4L B. 33.6L

C. 6.72L D. 无法求解

解析：很多学生会考虑设三种金属的物质的量，用方程组求解而误入歧途，最后只能选D。

若从数值特征上把握，从三种金属混合物44g到无水固体140g，增加的恰是SO42-的质量，为96g，即1mol，又知恰好完全反应，则产生的H2也是1mol，所以A项正确。

责任编辑 罗 峰