Laplacian正则项半监督不平行超平面分类机

闫金花　杨志霞

摘要：本文通过引入拉普拉斯（Laplacian）正则项，针对半监督分类问题我们建立了基于拉普拉斯正则项的半监督不平行超平面分类机。和经典的双支持向量机相比，该算法不仅继承了不平行超平面决策的优点，并且将其推广到了半监督分类问题中。最后在人工数据上进行数值实验，与拉普拉斯双支持向量机和拉普拉斯支持向量机做比较，数值结果表明我们提出算法的可行性和有效性，特别是对于交叉型数据集，基于拉普拉斯正则项的半监督不平行超平面分类机具有明显较高的分类精确度。

关键词：支持向量机 半监督分类问题 拉普拉斯正则项 不平行超平面分类机

中图分类号：TP181 文献标识码：A 文章编号：1007-9416（2016）06-0221-04

Abstract：In this paper， we have proposed a novel Laplacian nonparallel hyperplanes classifier for the semi-supervised classification problem.Compared with the twin support vector machine， it has the advantage of nonparallel hyperplanes classifier and can be used for the semi-supervised classification problem. Finally， compared with the Laplacian twin support vector machine and the Laplacian support vector machine， the results of experiments on artificial dataset and UCI datasets show that our method is feasible， especially for“Cross Planes”datasets.

Key Words：Support vector machine； Semi-supervised classification problem； Laplacian regularization； Nonparallel hyperplanes classifier

1 引言

机器学习在人工智能的研究中具有非常重要的地位。支持向量机是Vapnik等在统计学习理论基础上发展起来的针对小样本的机器学习方法[1]。该方法由于具有较强的泛化能力、方便对高维的数据进行操作而得到了日益广泛的研究和应用。传统的有监督的分类方法，虽然能够有效地解决各种实际问题，但是需要事先对大量样本进行标记以获取足够的训练样本，代价高，效率低。因此，根据实际需要研究人员提出了一些半监督支持向量机分类方法。Bennett， K.，& Demiriz，A.于1999年提出了半监督支持向量机（S3VM[2]），它基于聚类假设，试图通过探索未标记数据来规范调整决策边界，从而提高运算的准确度。21世纪以来，Melacci，S.，&Belkin，M提出了拉普拉斯（Laplacian）支持向量机[3]，主要是通过图的拉普拉斯矩阵来探索数据的流形结构，通过对无标记的数据找到合适的类别，以使它们与已标记的数据和潜在的图的结构的不一致性最小化，从而提高了预测精确度。

本文将拉普拉斯（Laplacian）正则项引入到不平行超平面分类机[4]之中，建立了拉普拉斯正则项的半监督不平行超平面分类机。同时，在数值试验中，从精度和速度上，和经典的拉普拉斯正则项支持向量机和拉普拉斯正则项双支持向量机做了对比，表明了提出的算法的优良性。

2 背景知识

4 数值实验

这一节通过数值实验来检验基于拉普拉斯正则项的不平行超平面分类机（Lap-NHSVM）。具体地，主要由分类准确率和计算时间作为判别指标，与拉普拉斯支持向量分类机（Lap-SVM）、拉普拉斯双支持向量分类机（Lap-TSVM）作对比，这里考虑了线性和非线性两种情形。利用UCI数据库中的六组数据。本文中核函数定为高斯核，在实验中参数均选自于集合随机的选取30%的数据集通过十折交叉检验法[1]来确定参数。数值实验在Windows 7系统上完成，处理器为英特尔酷睿双核，主频为 2.2GHz，内存为2GB。程序代码基于Matlab R2010a平台上完成。具体的算法我们采用逐次松弛迭代算法（SOR）[4]。

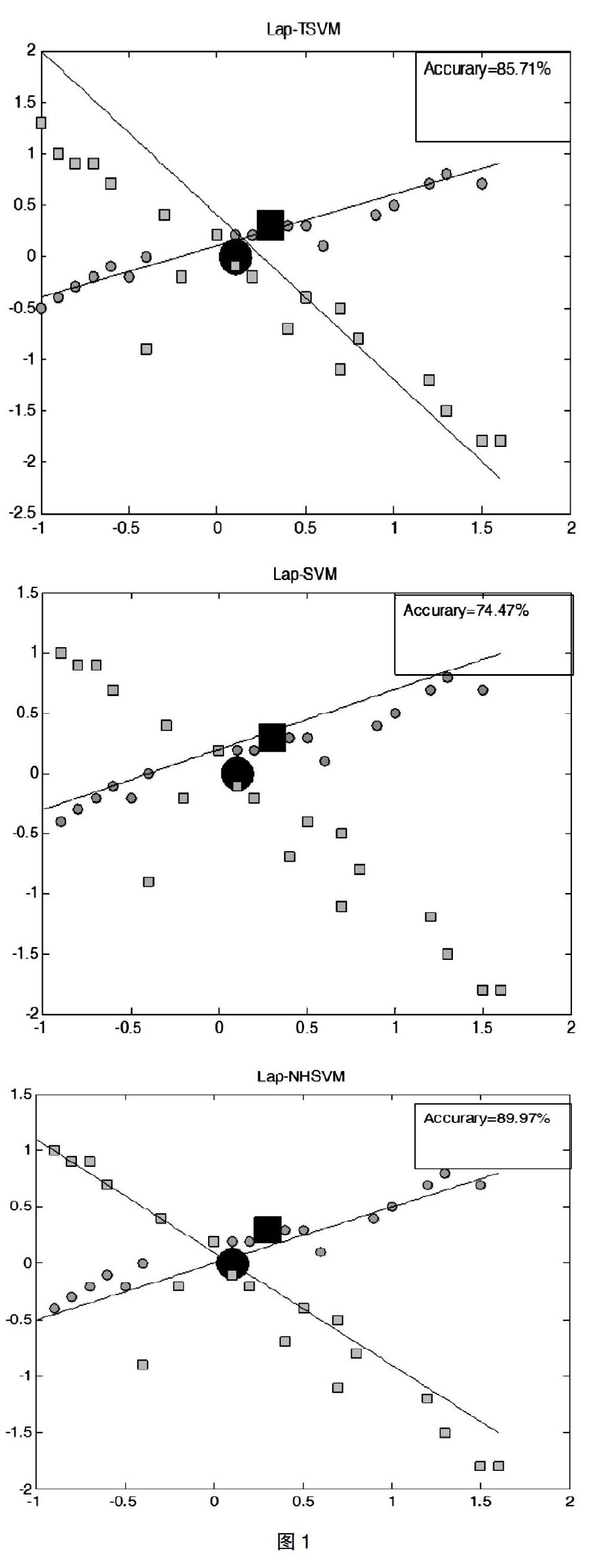
图1表示Lap-SVM，Lap-TSVM和Lap-NPSVM的分类比较，小正方形代表有标签正类样本点，大正方形代表无标签正类样本点，小圆代表有标签负类样本点，大圆代表无标签负类样本点。

Lap-TSVM和Lap-NHSVM做对比，从图1可以看出Lap-NHSVM具有明显比较好的分类精度，能够更好的利用未标签的数据，从而使分类效果更好。

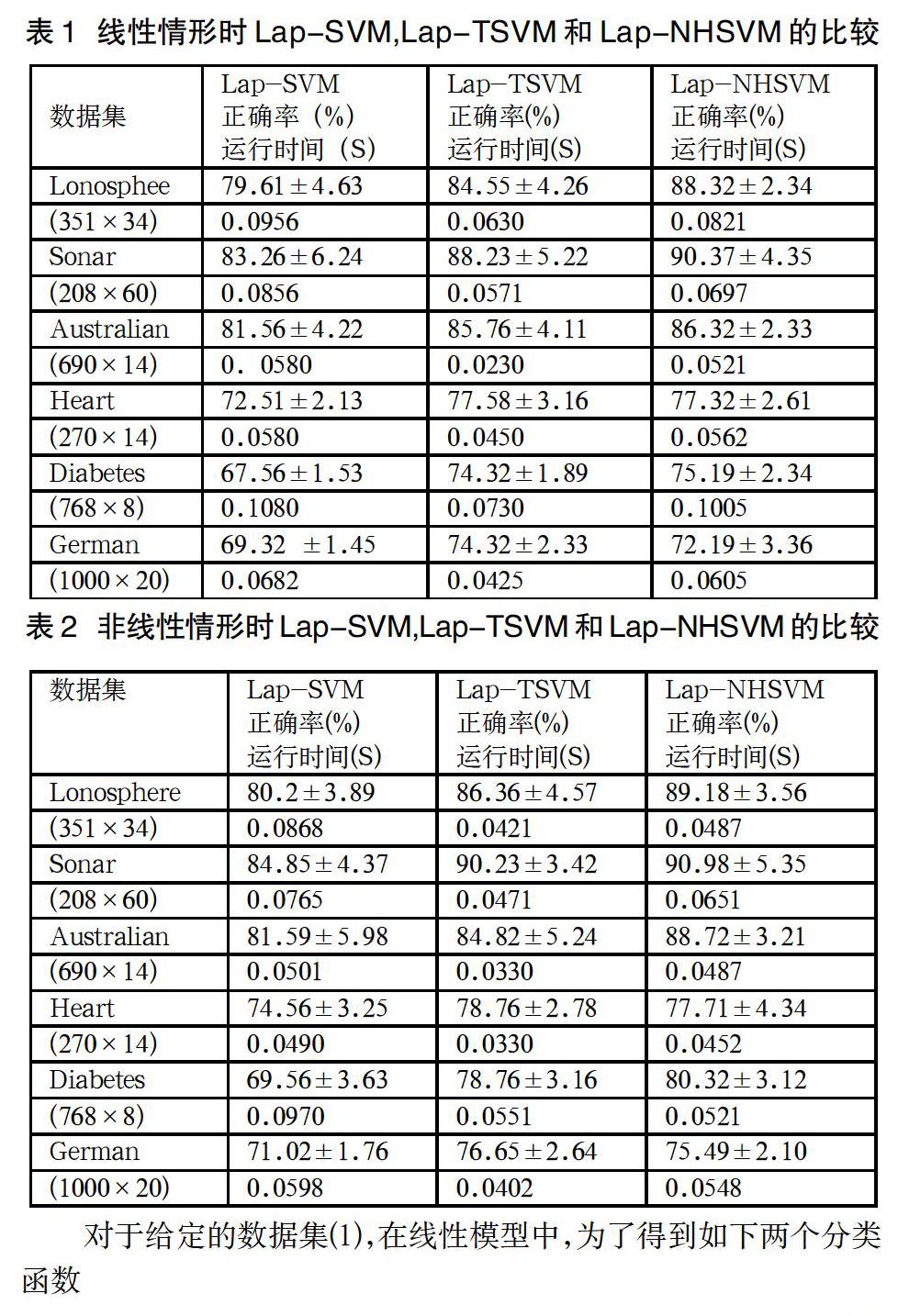
在下面表1和表2的实验中，我们利用UCI数据中的六个数据来做数值实验，包括Diabetes，German，Ionosphere，Sonar，Australian，Heart。在机器学习中，这些数据经常会被用来检测算法的优劣，在实验中，取每个数据集的40%作为有标签的样本集，30%作为无标签的样本集，进行十次试验，取十次实验结果的平均值加减方差构成。对于CPU时间，同样取十次实验结果的平均值。如图所示，黑体表示最高精确度对应的数据，表1表示线性情形时，Lap-SVM，Lap-TSVM和Lap-NHSVM的比较，表2表示非线性情形时，Lap-SVM，Lap-TSVM和Lap-NHSVM的比较，从实验结果可以明显的看出，对于大部分数据集，拉普拉斯不平行超平面分类机具有更高的分类精确度，例如，对于Lonosphere数据集，Lap-NHSVM对应的精确度为88.32%，而Lap-SVM，Lap-TSVM对应的精确度远小于它，另一方面，从下表可以看出，Lap-NHSVM对应的CPU时间要比Lap-SVM的快速，却比Lap-SVM和Lap-TSVM的精确度高。

5 结语

在本文中，提出了基于拉普拉斯正则项的半监督不平行超平面分类机，从数值实验可以看出，提出的分类方法具有较高的分类精确度，尤其对于某些数据集，例如交叉数据集，我们的算法可以得到更精准的结果，因此我们可以看出，本文提出的半监督不平行超平面分类方法值得肯定。

参考文献

[1]V.Vapnik.The Nature of Statistical Learning Theory. Springer-Verlag， 2nd edition， 1998.

[2]Bennett，K.，& Demiriz， A. （1999）. Semi-supervised support vector machines.In Advances in Neural Information Processing Systems 11， 368-374.

[3]Melacci，S.，&Belkin，M（2011）.Laplacian support vector machines trained in the primal.Journal of Machine Learning Research，12.

[4]Shao Y H， Chen W J， Deng N Y. Nonparallel hyperplane support vector machine for binary classification problems[J]. Information Sciences263（2014）22-35.

[5]Belkin et al.，（2006）.Manifold regularization；a geometric framework for learning from labeled and unlabeled examples.Journal of Machine Research，7，2399-2434.

[6]O.L. Mangasarian， E.W. Wild， Multisurface proximal support vector classification via generalize deigenvalues， IEEE Transactions on Pattern Analysisand Machine Intelligence28 （1）（2006） 69-74.

[7]邓乃扬，田英杰.数据挖掘中的新方法-支持向量机[M].2版.北京：科学出版社，2009：356-357.

[8]O.L.Mangasarian， E.W. Wild， Multisurface proximal support vector classification via generalize deigenvalues， IEEE Transactions on Pattern Analysisand Machine Intelligence 28 （1） （2006） 69-74.

[9]Y.H.Shao，C.H.Zhang，X.B.Wang， N.Y. Deng， Improvements on twin support vector machines，IEEE Transactions on Neural Networks 22（6）（2011）962-968.