多封隔器密闭环空热膨胀力学计算方法及应用
张 智 王 汉
“油气藏地质及开发工程”国家重点实验室·西南石油大学
多封隔器密闭环空热膨胀力学计算方法及应用
张智 王汉
“油气藏地质及开发工程”国家重点实验室·西南石油大学
张智等. 多封隔器密闭环空热膨胀力学计算方法及应用. 天然气工业, 2016,36(4):65-72.
摘 要环空温度压力变化对高温高产气井多封隔器管柱力学行为和安全可靠性的影响较大。为此,基于动量守恒定律、能量守恒定律及各层环空流体瞬态传热机理,建立了单层和多层环空的温度、压力场计算模型,分析全井筒环空温度和热膨胀压力的变化规律;针对多封隔器完井管柱,综合考虑密闭环空温度效应和体积变化效应,建立了多封隔器间密闭环空热膨胀压力计算模型,研究双封隔器间密闭环空的热膨胀压力变化规律;以南海西部某高温高产气井作为实例开展分析。结果表明:①环空温度效应和体积效应共同作用使全井筒A环空热膨胀压力最小,C环空热膨胀压力最大;②双封隔器间密闭环空热膨胀压力与环空温差基本上呈线性关系,温度效应引起的压力增量占主导作用,体积效应对压力增量的贡献率随环空温差的增大而增大;③确定实例井最大产气量为212×104m3/d,在产量为160×104m3/d时,双封隔器最大坐封间距为312 m。结论认为:在强度允许的前提下,选择内径较大的生产套管有利于降低密闭环空热膨胀压力。
关键词多封隔器 高温高产 气井 密闭环空 热膨胀压力 力学计算 安全评价
在高温高产气井测试及生产过程中,如果完井管柱采用双封隔器结构且未与地层连通,环空体积不变,随温差的加大,多封隔器间密闭环空内流体热膨胀压力急剧增加,可能造成油管抗挤不足和生产套管抗内压不足,引起油管断脱或封隔器破坏失效等恶性事故[1-3]。准确掌握井筒压力、温度分布,为校核油套管柱以及封隔器强度提供基础数据,对油气井动态分析和安全生产有着至关重要的意义[4]。李子丰、樊洪海、冯建华等[5-7]建立了封隔器复合管柱受力分析模型,车争安等[8]研究了全井筒环空热膨胀带压机理,张波、杨进等[9-10]结合PVT状态方程建立了深水套管环空压力预测模型。以上学者都没有分析多封隔器间完井管柱的力学行为和密闭环空的热膨胀机理,不能准确评价和分 析多封隔器间油套管安全性及环空热膨胀压力。为此,笔者根据多封隔器密闭环空所处环空层数,建立了单层和多层环空温度场和多封隔器密闭环空热膨胀压力计算模型,结合实例井分析了双封隔器密闭环空热膨胀压力及管柱安全的影响因素,以期为高温高产气井完井方法优化和确定合理生产制度提供更为可靠的理论依据。
1 环空温度场计算模型
从图1可知井筒中一般含有多个环空,随着完井管柱多封隔器坐封位置的不同,可分为单层环空传热和多层环空传热,需要分别建立单层环空和多层环空的温度场计算模型。
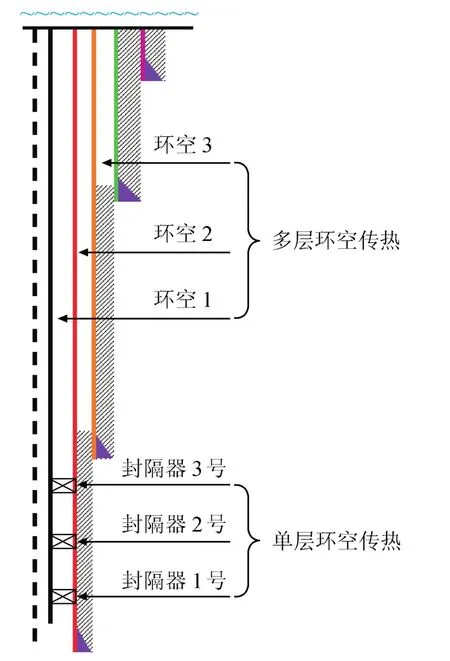
图1 环空示意图
1.1 单层环空温度计算模型
图2为单层环空传热示意图,由能量守恒定律可知,环空流体热量增量等于油管流体流入环空的热量QiA减去环空流入地层的热量QoA,单层环空传热控制方程:

图2 单层环空传热示意图

式中m表示单位长度环空流体质量,kg/m;cp表示环空流体比热容,J/(kg·℃);T1表示环空流体温度,℃;t表示生产时间,s;r1o表示环空外半径,m;rco表示套管外半径,m;Tf表示油管内流体温度,℃;Usig表示单层环空总传热系数,J/(s·m2·℃);Tei表示原始地层温度,℃;ke表示地层导热系数,J/ (s·m·℃);TD表示无因次生产时间,无量纲。详细计算见过程本文参考文献[11]。
式(1)为一阶线性微分方程,可以解得:

式中rto表示油管外半径,m;rti表示油管内半径,m;T10表示井筒开始生产前环空流体温度,℃;LR1表示单层环空松弛参数,m–1;详细计算过程见本文参考文献[12]。
1.2 多层环空温度计算模型
对于井筒来说,考虑井筒全瞬态传热模式,垂向传热相对于径向传热几乎可以忽略不计[13],建立井筒温度与时间和径向距离关系的二阶微分方程:式中α表示环空流体热扩散系数,s/m2;r表示环空半径,m;T表示环空温度,℃;t表示开采时间,s。
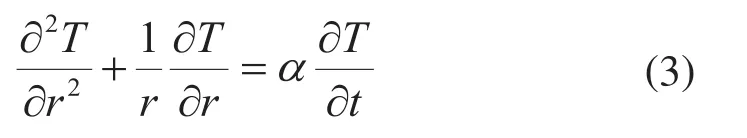
式(3)的解析解为:
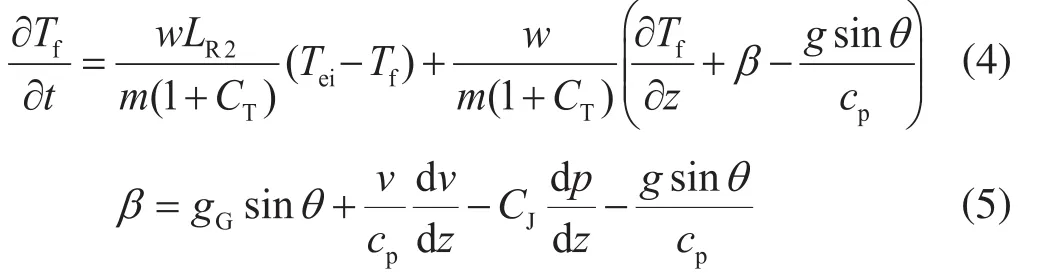
式中CT表示热量储存系数,无量纲;CJ表示焦耳—汤姆逊系数,℃/MPa;LR2表示多层环空松弛参数,m–1;w表示质量流量,kg/s;gG表示地温梯度,℃/m;θ表示井斜角,(°);v表示流体流速,m/s;β表示中间变量,℃/m;p表示流体压力,MPa。
对式(4)进行积分可得油管流体温度:

式中Umul表示多层环空总传热系数,J/(s·m2·℃);L表示井深,m;z表示从井底到井口轴线上任意深度,m。
沿井筒垂直方向作多个同心圆柱以计算开采过程中各个环空热量和质量的流动情况,沿径向划分圆柱形体积单元网格来表示热量从油管内流体传向环空流体的情况(图3),每一个网格代表一个环空,Tj表示第j个环空温度。
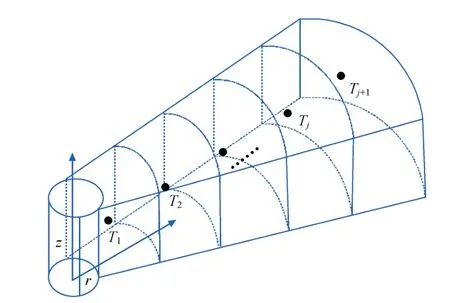
图3 多层环空体积单元网格划分图
在非稳态径向系统中,采用傅里叶法则计算每一个体积单元网格j的传热情况,即:

式中hc表示环空流体对流换热系数,J/(s·m2·℃);kj表示第j层环空流体导热系数,J/(s·m·℃);n表
示迭代计算次数;Δrj表示第j层环空外半径与第j-1层环空外半径的差值,m;ρ表示环空流体密度,g/ cm3。
令
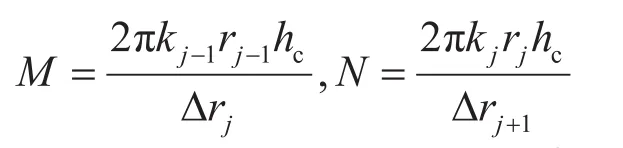

式(9)是全隐式的,可以通过矩阵形式求解,对于一个有三个网格的圆柱体井筒单元,其求解矩阵为:
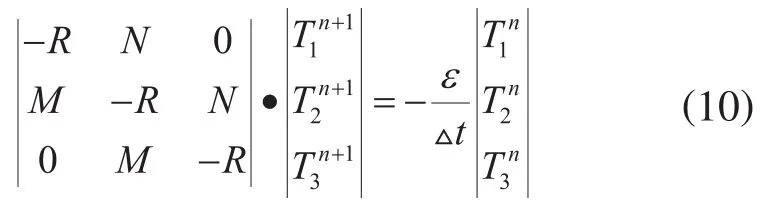
式(10)中T1的初始值用本文的解析模型求出。
1.3 环空总传热系数计算[14-18]
1.3.1 单层环空总传热系数
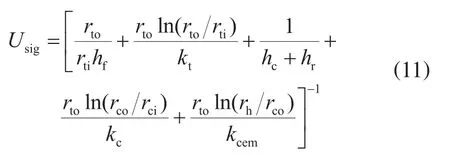
式中kt表示油管导热系数,J/(s·m·℃);kc表示套管导热系数,J/(s·m·℃),由于管材的热力学性能会随着温度变化,所以需要迭代计算;rh表示井眼半径,m;rci表示套管的内半径,m;kcem表示水泥环导热系数,J/(s·m·℃);hr表示环空流体辐射传热系数,J/(s·m2·℃);hf表示油管内流体对流换热系数,J/(s·m2·℃)。
1.3.2 多层环空总传热系数
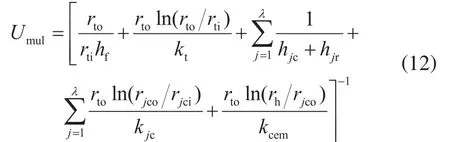
式中λ表示环空总层数(λ≥2);hjc表示第j层环空流体对流换热系数,J/(s·m2·℃);hjr表示第j层环空流体辐射传热系数,J/(s·m2·℃);rjco表示第j层环空外套管的外半径,m;rjci表示第j层环空外套管的内半径,m;kjc表示第j层环空外套管导热系数,J/(s·m·℃)。
2 双封隔器密闭环空热膨胀压力计算模型
封隔器、油管、井下安全阀及流动短节作为井筒第一安全屏障,封隔器和油管的强度和密封完整性在气井整个生命周期中显得尤为重要[19-20]。
双封隔器间油套环空完全密封,无流体渗入或泄露,环空流体质量变化引起的压力变化为零,即双封隔器间密闭环空流体热膨胀压力由环空体积变化效应和流体热膨胀效应组成,而密闭环空体积变化(ΔVann)由油管径向热膨胀导致的环空体积变化(ΔV1),油管径向压缩导致的环空体积变化(ΔV2),环空流体热膨胀导致的体积变化(ΔV3),环空流体被压缩导致的体积变化(ΔV4)组成[21]。即双封隔器密闭环空压力变化的控制方程:
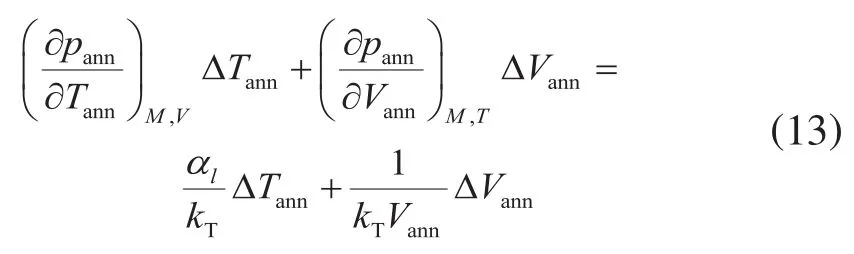
其中
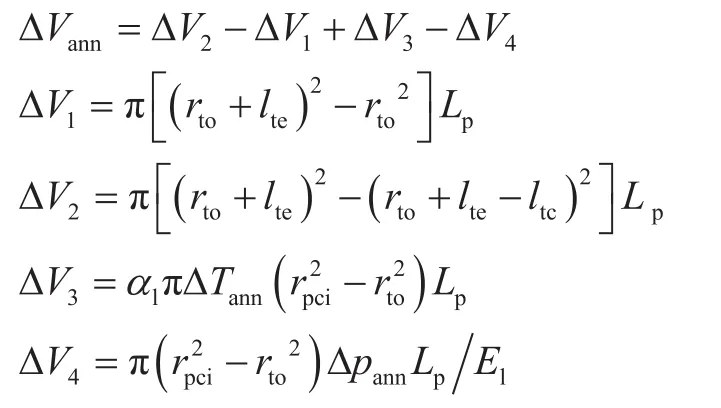
式中Δpann表示双封隔器间环空压力变化量,MPa;ΔTann表示双封隔器间环空流体温度变化量,℃;kT表示环空流体的等温压缩系数,1/MPa;αl表示环空流体热膨胀系数,1/℃;rpci表示生产套管内半径,m;El表示环空流体体积模量,MPa;Lp表示双封隔器坐封间距,m;lte、ltc分别表示环空温度变化和压力变化引起的油管径向位移,m。
在高温高产气井中,环空流体在温差作用下,由于封隔器及管壁的约束,不能自由膨胀,造成压力升高,进而挤压油管,使环空体积增大,而体积增加会降低环空压力值,使环空体积又趋于减小,环空体积减小使流体受压缩产生额外压力,该压力反过来又作用于油管,使环空体积再次发生改变,而体积的改变又使得压力发生变化。因此,它们是耦合作用的[22]。需要通过迭代法求解Δpann,具体求解步骤如图4所示。图4计算环空压力变化流程为:先假设初值并将其带入式(13),求出ΔVann,进而可求得对应的Δpann;然后将求得的Δpann带入式(13),求出新的ΔVann,继续运算得到新的Δpann,比较两次算出的Δpann,如果差值在允许范围内,则输出Δpann,否则重新迭代计算直到达到所要求的精度为止。

图4 流体热膨胀引起环空压力变化计算流程图
3 算例分析
南海西部某高温高产气井水深988.3 m,完钻井深4 503 m,地温梯度为0.03 ℃/m,井底温度为152℃,地层压力为75 MPa,产量160×104m3/d,其井身结构如图5所示。
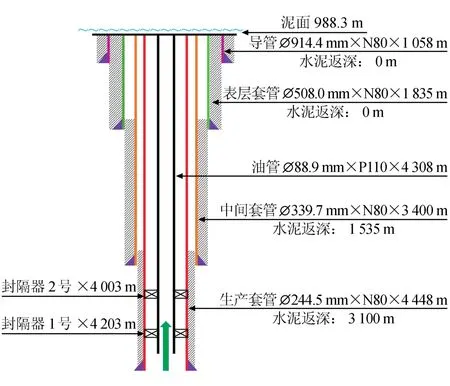
图5 南海某深水井井身结构图
该井封隔器1号坐封深度4 203 m,封隔器2号坐封深度4 003 m,油管导热系数45 J/(s·m·℃),套管导热系数55 J/(s·m·℃),环空流体热膨胀系数为0.000 45 ℃–1,流体等温压缩系数为0.000 485 MPa–1,环空流体体积模量2 200 MPa,油管热膨胀系数12.5×10–6℃–1,套管热膨胀系数12×10–6℃–1,油套管弹性模量为225 GPa,泊松比为0.35,天然气相对密度0.68,环空流体密度为1.20 g/cm3,环空流体比热容为4 235 J/(kg·℃),气体比热为4 244 J/ (kg·℃),水泥环导热系数为0.62 J/(s·m·℃),地层导热系数为2.215 J/(s·m·℃)。
3.1 全井筒环空温度及热膨胀压力
图6为全井筒的环空温度分布情况,可以看出:随着井深的增加各环空的温度逐渐增加,在同一井深处油管流体温度高于A环空(油管和生产套管环空)流体温度高于B环空(生产套管和中间套管环空)流体温度高于C环空(中间套管和表层套管环空)流体温度,从井底到井口过程中,各环空流体的温度差异越发明显,这主要是因为流体在井筒中向上流动过程中径向的环空层数增加,井下组件数增加,总传热系数减小。因此井筒径向温度梯度变大。

图6 环空温度场图
图7为全井筒环空热膨胀压力与产量的关系,可以看出:全井筒A、B、C环空的热膨胀压力随气井产量的增大而增大,且增加趋势由急变缓,当产量小于180×104m3/d时,环空热膨胀压力增加的趋势较大,当产量超过180×104m3/d时环空热膨胀压力增加趋势逐渐平缓直至稳定。这主要是因为当产量增大到一定程度时,井筒传热量和环空流体的热力学参数不会无限的增大,所以环空热膨胀效应最终趋于稳定;当产量一定时,C环空的热膨胀压力高于B环空高于A环空,虽然图6显示C环空的温度最小,A环空最大,而环空热膨胀压力由环空温度效应和体积效应产生,此时A环空的深度约为C环空深度的2.8倍,其环空温差明显小于C环空,造成C环空的热膨胀压力最大,A环空最小。因此在预测密闭环空的热膨胀压力时应该综合考虑温度效应和体积效应。
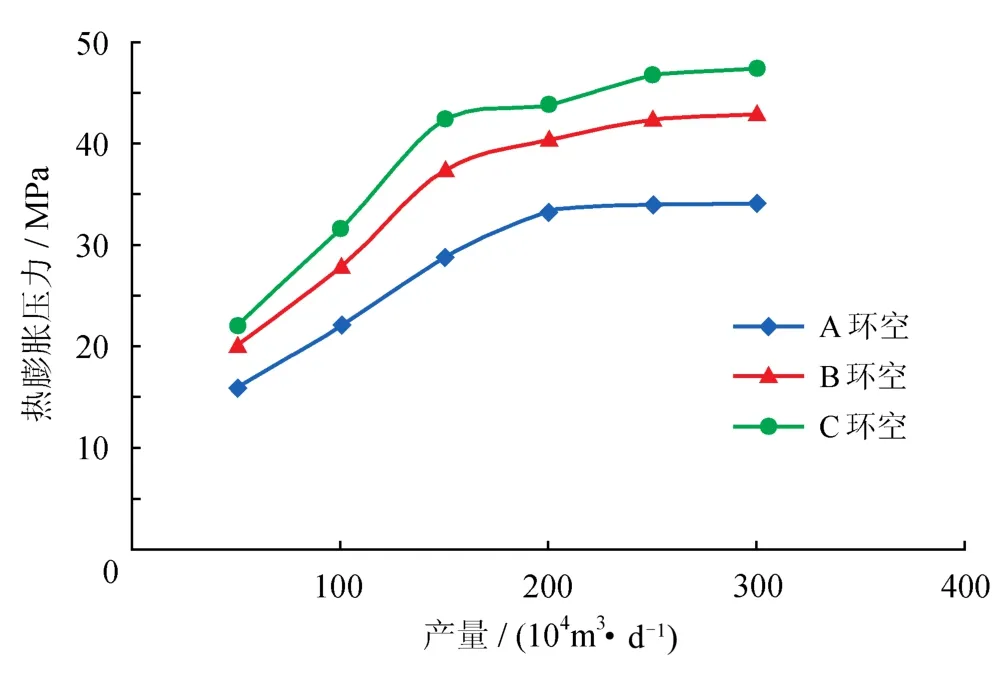
图7 全井筒环空热膨胀压力图
3.2 双封隔器密闭环空热膨胀压力
图8为A环空双封隔器密闭环空热膨胀压力与两个封隔器坐封间距以及环空流体的热膨胀系数的关系,气井产量为160×104m3/d。
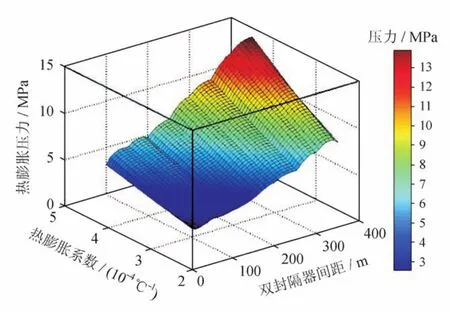
图8 双封隔器间密闭环空热膨胀压力变化规律图
从图8中可以看出:密闭环空热膨胀压力随着双封隔器坐封间距的增大而增大,这主要是由于双封隔器密闭环空始终处于A环空之中,随着其坐封间距的增大,双封隔器密闭环空的温差越大,此时环空体积优势不明显,所以其热膨胀压力越大;同一坐封间距下,环空流体的热膨胀系数越大,密闭环空的热膨胀压力越大。由于此时不考虑井筒的腐蚀情况,根据API RP90[23]标准计算得到A环空最大允许带压值为13.5 MPa,可以得出当环空流体热膨胀系数为0.000 35 ℃–1时,双封隔器的最大坐封间距为312 m;在确定了双封隔器的坐封间距时,根据流体热力学性质可合理选择环空保护液类型。
图9为只考虑密闭环空温度效应时环空压力增加值与环空温差和气井产量的关系,图10为只考虑密闭环空体积效应时环空压力增加值与环空温差和气井产量的关系。可以看出:对于该高产气井,双封隔器间环空压力增加值与环空温差和产量基本上呈线性正相关,

图9 只考虑温度效应时密闭环空压力增加值变化规律图
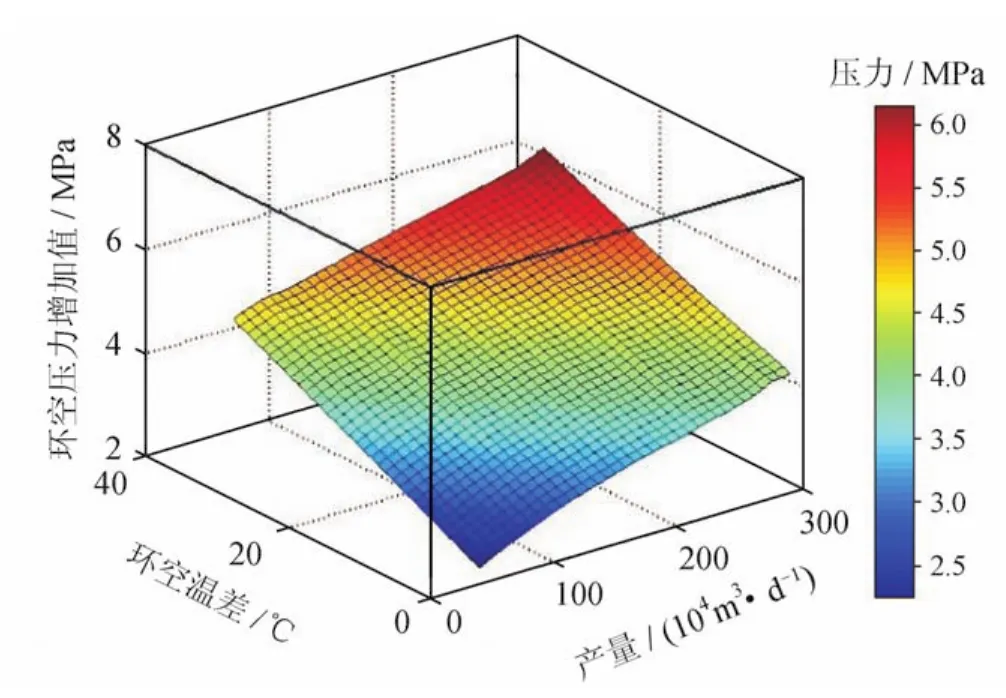
图10 只考虑体积效应时密闭环空压力增加值变化规律图
在两种效应中,环空温度效应引起的压力变化占据主导作用,当产量达到250×104m3/d时,温度效应导致的压力增加值为体积效应的4.8倍。而随着气井产量的增大,较大的温差会加剧管柱和环空流体热膨胀和压缩膨胀效应,从而导致环空体积发生较大变化,此时环空体积效应对环空压力的贡献率会逐渐增大。所以,对于特定材料的油套管,如果生产作业时密闭环空温度增加到某一阀值,环空热膨胀压力就会超过油管的抗外挤强度或生产套管的抗内压强度,发生管柱挤毁或破裂事故,尤其是封隔器1号的坐封位置如果发生泄漏,气体窜入A环空会形成严重的环空带压,存在极大的安全隐患。因此必须在生产过程中引入环空带压管理,对各环空进行放压,否则会产生严重的套损,导致环空负压数百上千米。故分析双封隔器间密闭环空热膨胀效应对油气井安全生产具有重要意义。
图11为油管抗外挤安全系数与气井产量和双封隔器密闭环空热膨胀压力的关系,图12为生产套管抗内压安全系数与气井产量和双封隔器密闭环空热膨胀压力的关系,双封隔器的坐封间距为200 m。从图11、12中可以看出:随着产量的增加密闭环空热膨胀压力增加,油管抗外挤安全系数和生产套管的抗内压安全系数降低,设定抗外挤安全系数和抗内压安全系数为1是油管和生产套管的安全工作临界值[24],气井产量增加导致密闭环空热膨胀起压,该热膨胀压力的聚集增加了油管和生产套管被破坏的可能性。对于该高温高产气井,当产量达到211×104m3/d时,油管的抗外挤安全系数为1.023,生产套管的抗内压安全系数为1.22,处于安全状态;当产量为212×104m3/d时,油管的抗外挤安全系数为0.958,生产套管的抗内压安全系数为1.20,此时油管被挤爆,生产套管安全,因此可以确定该气井的生产指标不能超过212×104m3/d。
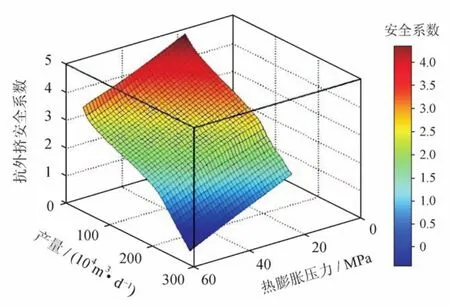
图11 油管抗外挤安全系数变化规律图
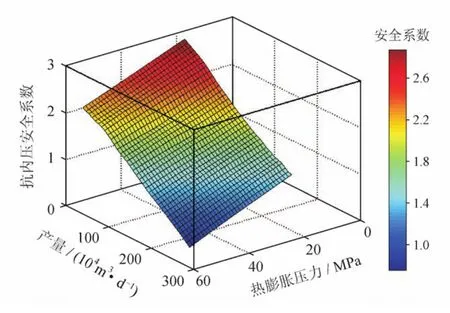
图12 生产套管抗内压安全系数变化规律图
根据现场常用的不同类型Ø244.5 mm套管的数据参数,分析Ø244.5 mm生产套管内径对密闭环空热膨胀压力的影响(图13),从图13中可以看出,随着套管内径的增大,密闭环空热膨胀压力减小,并且减小幅度随着套管内径的增大逐渐降低,这主要是由于在相同的温差下,大环空的热膨胀效果降低,密闭环空体积改变反而不明显,造成环空体积变化引起的压力增量减小。因此在强度允许条件下尽量选择内径较大的生产套管。
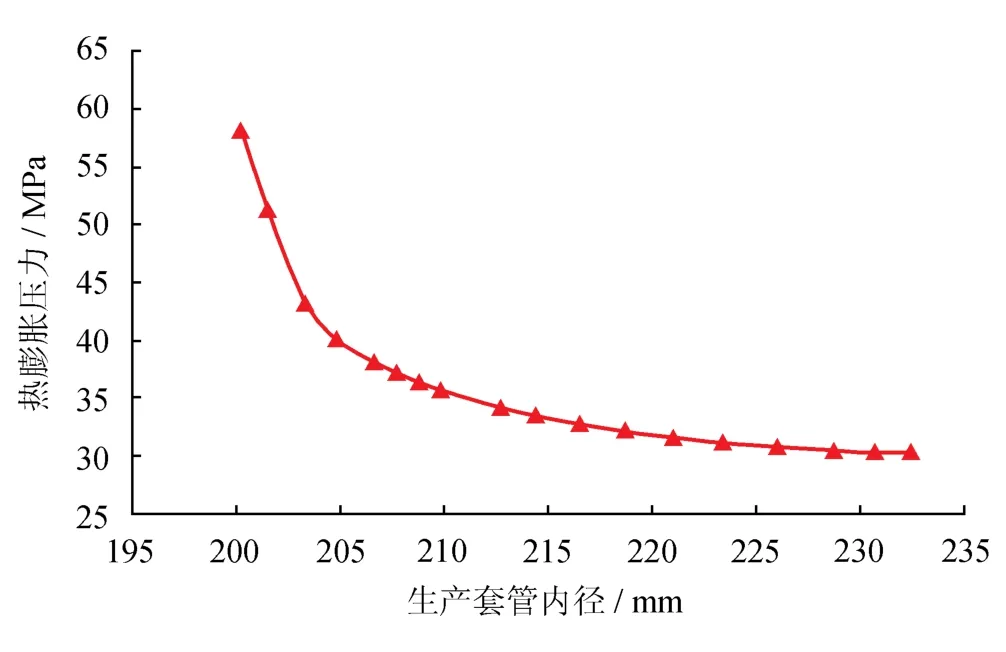
图13 密闭环空压力变化量随套管内径变化曲线图
4 结论
1)根据动量守恒定律和能量守恒定律,建立了单层环空和多层环空的温度计算模型,划分环空体积单元网格,采用矩阵分析和递推循环迭代法求解全井筒环空温度、压力场;基于双封隔器密闭环空流体和油套管的热膨胀和压缩效应,建立了多封隔器间密闭环空热膨胀压力的计算模型,采用迭代法耦合求解。
2)对于全井筒环空:A环空温度最大,C环空温度最小,综合考虑温度效应和体积效应,得出A环空热膨胀压力最小,C环空热膨胀压力最大,在投产过程中需要引入环空带压管理,合理选择环空流体类型,对各环空进行放压,否则可能导致油套管损坏。
3)对于双封隔器密闭环空,热膨胀压力随封隔器坐封间距和流体热膨胀系数的增大而增大;环空热膨胀压力与温差基本呈线性正相关,且温度效应引起的压力增量占主导地位,但环空体积效应对压力增量的贡献率随环空温差的增大而增大。
4)对于南海某高温高产气井,建议双封隔器坐封间距不超过312 m,投产产量不超过212×104m3/ d;在强度允许的前提下,选择内径较大的生产套管有利于降低密闭环空热膨胀压力。
参 考 文 献
[1] Adams AJ, MacEachran A. Impact on casing design of thermal expansion of fuids in confned annuli[J]. SPE Drilling & Completion, 1994, 9(3): 210-216.
[2] 张智, 黄熠, 李炎军, 张超, 曾春珉. 考虑腐蚀的环空带压井生产套管安全评价[J]. 西南石油大学学报: 自然科学版, 2014, 36(2): 171-177. Zhang Zhi, Huang Yi, Li Yanjun, Zhang Chao, Zeng Chunmin. Safety evaluation of production casing considering corrosion in gas well with sustained casing pressure[J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2014, 36(2): 171-177.
[3] 肖太平, 张智, 石榆帆, 周晓昱, 顾南, 蒋芸, 等. 基于井下作业载荷的A环空带压值计算研究[J]. 钻采工艺, 2012, 35(3): 65-66. Xiao Taiping, Zhang Zhi, Shi Yufan, Zhou Xiaoyu, Gu Nan, Jiang Yun, et al. Research on annulus A sustained casing pressure based on downhole work load[J]. Drilling & Production Technology, 2012, 35(3): 65-66.
[4] 王波. 高温高压完井管柱力学分析及安全评价[D]. 成都: 西南石油大学, 2014. Wang Bo. HPHT completion string mechanical analysis and safety evaluation[D]. Chengdu: Southwest Petroleum University, 2014.
[5] 李子丰, 蔡雨田, 李冬梅, 徐燕东. 地层测试管柱力学分析[J].石油学报, 2011, 32(4): 709-716. Li Zifeng, Cai Yutian, Li Dongmei, Xu Yandong. Mechanical analysis of pipe string in formation testing[J]. Acta Petrolei Sinica, 2011, 32(4): 709-716.
[6] 樊洪海, 王宇, 张丽萍, 杨行, 杨向同, 魏峰. 高压气井完井管柱的流固耦合振动模型及其应用[J]. 石油学报, 2011, 32(3): 547-550. Fan Honghai, Wang Yu, Zhang Liping, Yang Hang, Yang Xiangtong, Wei Feng. A fuid-solid coupled oscillation model for completion string and its application in high pressure gas well[J]. Acta Petrolei Sinica, 2011, 32(3): 547-550.
[7] 冯建华, 罗铁军, 金学锋. 双封隔器复合管柱受力分析方法及应用[J]. 石油钻采工艺, 1993, 15(2): 54-62. Feng Jianhua, Luo Tiejun, Jin Xuefeng. Dual packer complex string stress analysis method and its application[J]. Oil Drilling & Production Technology, 1993, 15(2): 54-62.
[8] 车争安, 张智, 施太和, 涂军军, 向亮, 刘乃震. 高温高压含硫气井环空流体热膨胀带压机理[J]. 天然气工业, 2010, 30(2): 88-90. Che Zheng'an, Zhang Zhi, Shi Taihe, Tu Junjun, Xiang Liang, Liu Naizhen. Mechanism of annular fuid thermal expansion pressure in HTHP sour gas wells[J]. Natural Gas Industry, 2010, 30(2): 88-90.
[9] 张波, 管志川, 张琦. 深水油气井开采过程环空压力预测与分析[J]. 石油学报, 2015, 36(8): 1012-1017. Zhang Bo, Guan Zhichuan, Zhang Qi. Prediction and analysis on annular pressure of deepwater well in the production stage[J]. Acta Petrolei Sinica, 2015, 36(8): 1012-1017.
[10] 杨进, 唐海雄, 刘正礼, 杨立平, 黄小龙, 严德, 等. 深水油气井套管环空压力预测模型[J]. 石油勘探与开发, 2013, 40(5): 616-619. Yang Jin, Tang Haixiong, Liu Zhengli, Yang Liping, Huang Xiaolong, Yan De, et al. Prediction model of casing annulus pressure for deepwater well drilling and completion operation[J]. Petroleum Exploration and Development, 2013, 40(5): 616-619.
[11] 毛伟, 梁政. 气井井筒压力、温度耦合分析[J]. 天然气工业, 1999, 19(6): 66-69. Mao Wei, Liang Zheng. Coupling analysis of the pressure and temperature in gas well borehole[J]. Natural Gas Industry, 1999, 19(6): 66-69.
[12] Hasan R, Izgec B, Kabir S. Sustaining production by managing annular-pressure buildup[J]. SPE Production & Operations, 2010, 25(2): 195-203.
[13] 宋洵成, 管志川. 深水钻井井筒全瞬态传热特征[J]. 石油学报, 2011, 32(4): 704-708. Song Xuncheng, Guan Zhichuan. Full transient analysis of heat transfer during drilling fluid circulation in deep-water wells[J]. Acta Petrolei Sinica, 2011, 32(4): 704-708.
[14] 郭建春, 曾冀. 超临界二氧化碳压裂井筒非稳态温度—压力耦合模型[J]. 石油学报, 2015, 36(2): 203-209. Guo Jianchun, Zeng Ji. A coupling model for wellbore transient temperature and pressure of fracturing with supercritical carbon dioxide[J]. Acta Petrolei Sinica, 2015, 36(2): 203-209.
[15] Willhite GP. Over-all heat transfer coeffcients in steam and hot water injection wells[J]. Journal of Petroleum Technology, 1967, 19(5): 607-615.
[16] Hasan AR, Kabir CS, Wang Xiaowei. Wellbore two-phase fow and heat transfer during transient testing[J]. SPE Journal, 1998, 3(2): 174-180.
[17] Ramey Jr HJ. Wellbore heat transmission[J]. Journal of Petroleum Technology, 1962, 14(4): 427-435.
[18] Williamson R, Sanders W, Jakabosky T, James M, Griffith JE. Control of contained-annulus fluid pressure buildup[C]//SPE/ IADC Drilling Conference, 19-21 February 2003, Amsterdam, The Netherlands. DOI:http://dx.doi.org/10. 2118/79875-MS.
[19] 张智, 李炎军, 张超, 黄熠, 郭永宾, 罗黎敏, 等. 高温含CO2气井的井筒完整性设计[J]. 天然气工业, 2013, 33(9): 79-86. Zhang Zhi, Li Yanjun, Zhang Chao, Huang Yi, Guo Yongbin, Luo Limin, et al. Wellbore integrity design of high-temperature gas wells containing CO2[J]. Natural Gas Industry, 2013, 33(9): 79-86.
[20] 张智, 周延军, 付建红, 陈明, 李文飞, 施太和. 含硫气井的井筒完整性设计方法[J]. 天然气工业, 2010, 30(3): 67-69. Zhang Zhi, Zhou Yanjun, Fu Jianhong, Chen Ming, Li Wenfei, Shi Taihe. A method of well integrity design for sour gas wells[J]. Natural Gas Industry, 2010, 30(3): 67-69.
[21] 邓元洲, 陈平, 张慧丽. 迭代法计算油气井密闭环空压力[J].海洋石油, 2006, 26(2): 93-96. Deng Yuanzhou, Chen Ping, Zhang Huili. Calculating the pressure in sealed annulus in oil well by iterative method[J]. Offshore Oil, 2006, 26(2): 93-96.
[22] 高宝奎. 高温引起的套管附加载荷实用计算模型[J]. 石油钻采工艺, 2002, 24(1): 8-10. Gao Baokui. Practical model for calculating the additional load on casing by high temperature[J]. Oil Drilling & Production Technology, 2002, 24(1): 8-10.
[23] American Petroleum Institute. API RP90 Annular casing pressure management for offshore wells[S]. Washington DC: API Publishing Services, 2006.
[24] 国家发展和改革委员会. SY/T 5724—2008套管柱结构与强度设计[S]. 北京: 石油工业出版社, 2008. National Development and Reform Commission. SY/T 5724-2008 Design for casing string structure and strength[S]. Beijing: Petroleum Industry Press, 2008.
(修改回稿日期 2016-01-11 编 辑 凌 忠)
A calculation method for thermal expansion mechanics of sealed annulus between multiple packers and its application
Zhang Zhi, Wang Han
(State Key Laboratory for Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China)
NATUR. GAS IND. VOLUME 36, ISSUE 4, pp.65-72, 4/25/2016. (ISSN 1000-0976; In Chinese)
Abstract:For high-temperature and high-production gas wells, the mechanical behaviors, safety and reliability of strings with multiple packers are more affected by the change of annulus temperature and pressure. In this paper, therefore, a calculation model for the temperature and pressure fields of single-layer and multi-layer annulus was established on the basis of momentum conservation law, energy conservation law and transient heat transfer mechanism of fluid in each annulus. Annulus temperature and thermal expansion pressure were analyzed through the full hole. For completion strings with multiple packers, the calculation model for thermal expansion pressure of sealed annulus between multiple packers was built after temperature and volume change effects of sealed annulus were analyzed comprehensively. And based on the calculation model, the change rules of thermal expansion pressure in sealed annulus between dual packers were studied. And finally, a case study was conducted on a high-temperature and high-production gas well in the western South China Sea. It is shown that the thermal expansion pressure of annulus A is the minimum in the full wellbore and that of annulus C is the maximum under the joint action of the annulus temperature and volume effects. As for dual packers, there is basically a linear relation between the sealed annulus thermal expansion pressure and the annulus temperature difference, with the pressure increment caused by the temperature effect playing a leading role and the contribution of the volume effect to pressure increment rising with the increase of annulus temperature difference. It is confirmed that the maximum production rate of the case well is 212×104m3/d. And at the production rate of 160×104m3/d, the maximum setting spacing of dual packers is 312 m. It is concluded that the production casing with larger internal diameters is favorable for reducing the thermal expansion pressure of sealed annulus so long as the strength is allowable.
Keywords:Multiple packers; High temperature and high production; Gas wells; Sealed annulus; Thermal expansion pressure; Mechanics calculation; Safety evaluation
DOI:10.3787/j.issn.1000-0976.2016.04.010
基金项目:国家科技支撑计项目(编号:2011BAE25B04)、国家科技重大专项“大型油气田及煤层气开发”(编号:2011ZX05023-004)、四川省省属高校科技创新团队建设计划(编号:13TD0026)。
作者简介:张智,1976年生,教授,博士,博士生导师;主要从事石油工程教学和科研工作。地址:(610500)四川省成都市新都区新都大道8号西南石油大学明辨楼B510室。电话:13981828569。ORCID:0000-0001-5089-416X。E-mail:wisezh@126.com
通信作者:王汉,1990年生,硕士研究生;从事高危油气井安全评价研究工作。地址:(610500)四川省成都市新都区新都大道8号西南石油大学明辨楼B509室。电话:15281045320。E-mail:546604043@qq.com

