稀少控制条件下的高分辨率卫星影像区域网平差

马红，周智勇

(1.重庆市勘测院，重庆　401121；　2.重庆市地理国情监测工程技术研究中心，重庆　401121)



稀少控制条件下的高分辨率卫星影像区域网平差

马红1，2，周智勇1，2

(1.重庆市勘测院，重庆401121；2.重庆市地理国情监测工程技术研究中心，重庆401121)

摘要：从高分辨率卫星影像区域网平差的模型出发，针对高分辨率卫星影像CCD线阵推扫成像的特点，研究其基于有理多项式模型RPC(Rational Polynomial Coefficient，or Rapid Position Capability)和少量控制点的区域网平差算法，并对重庆某地区的WordView-2卫星影像进行区域网平差处理试验，统计不同控制点布设方案下平差处理的精度，试验结果表明在稀少控制条件下本文方法可以实现卫星影像的正射纠正，能满足地理国情普查、地形图测绘等方面的需求。关键词：RPC模型；区域网平差；高分辨率；仿射变换

1引言

从上世纪90年代初以来，随着航天传感器地面分辨率的大幅度提高，卫星遥感作为重要的对地观测技术，在国民经济和国防建设中发挥着举足轻重的作用。从遥感影像中提取地球空间信息，需要把其投影到某一固定的参照系统中并修正原始影像中存在的几何变形，以便进行影像的几何量取、符合分析及信息提取。如何将遥感影像精确地投影到规定的参照系统中，准确消除原始影像所存在的几何变形是遥感影像处理和应用的一项关键技术。通常情况下，卫星遥感影像几何纠正主要是根据控制点采用多项式拟合方法，在地面控制点数量足够且分布均匀的前提下，该方法能够获取较高的精度。然而，在沙漠、海洋、边境外等地面特征不明显或人员难以达到地区，地面控制点获取困难，研究缺少控制点的影像几何纠正尤为重要[1～3]。

2卫星成像的有理函数模型

有理多项式模型RPC(Rational Polynomial Coefficient，或Rapid Position Capability)，就是用两组不同的多项式表达从地面坐标(φ，λ，h)到影像行列坐标(I，J)的数学关系，将地面点坐标与其对应的像点坐标用比值多项式关联起来[3]。

(1)

其中，(P，L，H)是标准化后的地面点空间坐标(φ，λ，h)，(X，Y)是标准化后的像点坐标，NumI(P，L，H)、DenI(P，L，H)、NumJ(P，L，H)、DenJ(P，L，H)为三次多项式函数。地面坐标和相点坐标标准化原理为：

(2)

其中，φ0、λ0、h0、I0、J0表示标准化平移参数，φs、λs、hs、Is、Js表示标准化比例参数，这些参数与RPC模型的4个多项式系统共同存储在对应的RPC文件中[4]。在RPC模型中，用式中的一次项表示光学投影系统产生的误差，用式中二次项表示地球曲率、大气折射和镜头畸变等产生的误差，有式中的三次项表示相机震动等具有高阶分量的误差[5]。由于受到严格成像模型本身系统误差的影响和利用RPC拟合严格模型时自身局限性带来的残余系统误差影响[6，7]，使得在利用RPC模型来代替严格成像模型进行卫星影像定位时，误差较大，很难获得较高的精度。

3卫星影像区域网平差数学模型

基于有力函数模型的卫星影像区域网平差的基本原理是利用影像质检的相互约束关系来补偿有理函数模型的系统误差，从而提高卫星影像的定位精度。

分析卫星系统参数对影像几何精度的影响，需要纠正正行方向和列方向的误差，在校正此类误差时即可以在物方空间进行，也可以再像方空间进行[8，9]，本文采用定义在像方的放射变化来校正此类误差[10，11]，可以定义其变换模型为：

FI=a0+a1I+a2J-I′FJ=b0+b1I+b2J-J′

(3)

式中，(I′，J′)表示系统误差改正后的像方坐标，a0，b0为像方平移定向参数，a1、a2、b1、b2为像方二维反射变换定向参数，a0、a1、a2三个参数将改正传感器在扫描方向上位置和姿态误差所引起的影像列方向上的误差，b0、b1、b2三个参数将改正传感器在飞行方向上位置和姿态误差所引起的影像行方向的误差。

针对有重叠区域的多景影像，在重叠区域内量测一定量的连接点，将连接点和控制点相结构，作为有理函数区域网平差模型的初始观测值，带入区域平差中进行整体平差解求[4，12]。

对测区中的每一个连接点，误差方程为：

V=Bt+CX-A

(4)

对测区中的每一个控制点，误差方程为：

V=Bt-A

(5)

其中：

假定在区域平差模型中，参与平差的影像数量为n，连接点个数为m，控制点个数为p，则可将区域网平差的误差方式表示为：

v=c·dX-A

(6)

其中，C=[CACG]，dX=[dXADXG]T，CA表示卫星影像仿射变换参数矩阵，CG表示连接点物方坐标矩阵，A为残差向量。通过建立每个控制点和连接点在相应影像上的误差方程，可将区域网平差的误差方式式化法[5，6，12，13]，求得结果为：

dX=(CTC)-1CTA

(7)

4试验及结果分析

为进一步证明上述的区域网平差方法的可行性，本文选择重庆某地区的 WorldView-2卫星影像进行区域网平差试验。

4.1试验数据情况

本文采用2014年10月获取的重庆某地区的WorldView-2卫星影像进行试验，影像地面分辨率为 0.5 m，影像质量良好，极少量云层覆盖，覆盖面积约 947 km2，覆盖情况如图1所示；试验区域内共有GPS D级控制点33个，生产于2013年～2014年，平面坐标系统为重庆市独立坐标系(中央经线为E105)，高程基准为1985国家高程基准，精度满足 1∶2 000数字地形图测绘项目需求，这为评价区域网平差精度与像控点的数量、分布等关系提供了良好的数据基础。

4.2试验结果

理论上，RPC适用于地心坐标、地理坐标等不同的坐标系统和物方坐标，考虑到数据成果应用于地理国情普查，选择国家2000大地坐标系统下的平面直角坐标作为RPC中的物方坐标。在本文的试验中设计了5中不同的定向点布点方案，并用多余的控制点作为检查点来统计平差精度。方案1，在试验区布设1个控制点其余点作为检查点进行区域网平差；方案2，在试验区布设4个控制点其余点作为检查点进行区域网平差；方案3，在试验区布设9个控制点其余点作为检查点进行区域网平差；方案4，在试验区布设16个控制点其余点作为检查点进行区域网平差；方案5，在试验区布设所有控制点进行区域网平差。试验结果如表1、表2所示。

在精度分析过程中，采用定向点计算坐标与其野外实测坐标的较差计算得到中误差，检查点精度由各检查点的计算坐标与其野外测量坐标的较差计算得到。

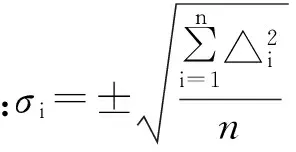
(8)

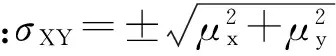
(9)

其中，△i(i=X，Y，Z)表示三个方向。

分析以上试验结果可知：在试验区中心布设一个控制点时，检查点的平面位置精度可以到达 3.07 m，高程精度可以达到 2.45 m，但是存在一定的系统误差； 随着布设的控制点逐步增多，控制点和检查点的精度逐渐趋于稳定，平面精度在 0.7 m左右，高程精度在 1 m左右，从数理统计的角度分析，不同的布点方案得到的精度没有明显差异，但最大误差会有变化。针对本文的实验区来说，利用WorldView-2卫星影像进行区域网平差，控制点在13个左右即可。

依据本文的试验结果，查阅《1∶5001∶10001∶2000地形图航空摄影测量内业规范》(GB/T 7930-2008)和《1∶50001∶100001∶50000地形图航空摄影测量内业规范》(GB/T 13990-1992)可知，本文试验结果可以满足 1∶5 000地形图基本定向残差和多余控制点不符值要求，不能满足 1∶2 000地形图的要求。本文方法可应用于地理国情普查、地形图测绘等项目中。

5结语

基于RPC模型的WorldView-2卫星影像区域网平差在布设少量控制点时即可满足一定的精度要求，利用高分辨率卫星遥感影像进行大比例尺测图将成为可能。从实验结果中控制点和检查点的数据来看，区域网平差阶段没有完全消除系统误差，在以后的研究工作中，还需要更多考虑系统误差的影响，进一步提高区域网平差的精度，降低系统误差对定向和测图的影响。

参考文献

[1]童小华，刘世杰，叶勤. 基于有理函数模型的QuickBird立体定位精度分析[J]. 同济大学学报·自然科学版，2009，37(4)：555～559.

[2]张过. 缺少控制点的高分辨率卫星遥感影像几何纠正 [D]. 2005.

[3]王红平，刘修国，罗红霞等. 基于RPC模型的IRS_P5影像正射校正 [J]. 地球科学·中国地质大学学报，2010，35(3)：485～489.

[4]代强玲，张宏伟，林宗坚. 稀少控制的多源卫星影像区域网平差研究[J]. 测绘科学，2014，39(9)：34～38.

[5]Toutin T. Review article：Geometric processing of remote sensing images：models，algorithms and methods[J]. International Journal of Remote Sensing. 2004，25(10)：1893～1924.[6]张永军，王蕾，鲁一慧. 卫星遥感影像有理函数模型优化方法[J]. 测绘学报，2011，40(6)：756～761.

[7]刘军，张永生，王冬红. 基于RPC模型的高分辨率卫星影像精确定位[J]. 测绘学报，2006，35(1)：30～35.

[8]张力，张继贤，陈向阳等. 基于有理多项式模型RFM的稀少控制SPOT_5卫星影像区域网平差[J]. 测绘学报，2009，38(4)：302～309.

[9]吴颖丹，明洋. 基于有理函数模型的多源SAR遥感影像区域网平差[J]. 测绘科学，2012，37(2)：49～51.

[10]李德仁，张过，江万寿等. 缺少控制点的SPOT_5HRS影像RPC模型区域网平差[J]. 武汉大学学报·信息科学版，31(5)：377～381.

[11]虞欣，贾光军，陈倬. 基于有理函数和像方仿射变换组合模型的高分辨率卫星影像区域网平差[J]. 测绘通报，2010(10)：4～10.

[12]叶勤，张小虎，刘世杰等. 基于直线特征的有理函数模型定位精度改善方法[J]. 同济大学学报·自然科学版，2010，38(2)：296～301.

[13]Hu Y，Tao C V. Updating solutions of the rational function model using additional control information[J]. Photogrammetric engineering and remote sensing. 2002，68(7)：715～724.

Block-Adjustment of High Spatial Resolution Satellite Images Based on Orbit-attitude Parameters

Ma Hong1，2，Zhou Zhiyong1，2

(1.Chongqing Survey Institute，Chongqing 401121，China；2.Chongqing Engineering Research Center of Geographic National Condition Monitoring，Chongqing 401121，China)

Key words：RPC Model；block-adjustment；high spatial resolution；affine transformation

Abstract：In this paper，We present a research on block-adjustment of high resolution satellite images based on Rational Function Model(RPC)with sparse GCPs，considering with the property of CCD line push-broom. We also make block-adjustment experimentation using WorldView-2 images of an area in Chongqing，and analysis the precision of block-adjustment with different control point setting projects. The results show the proposed method is effective on Ortho-calibration of satellite images with sparse GCPs，and can meet the needs of national geographical condition surveying，topographic map producing，and other applications.

文章编号：1672-8262(2016)03-76-03

中图分类号：P236

文献标识码：A

*收稿日期：2016—02—29

作者简介：马红(1987—)，女，工程师，主要从事摄影测量与遥感、地理国情监测方面技术研究与应用。

基金项目：住房和城乡建设部2015年科学技术研究开发项目课题(2015-K8-009)