产业发展与城市土地利用关系研究
——利用有约束条件的似乎不相关回归模型分析
◎ 丁成日 牛 毅 何莲娜 李 智
产业发展与城市土地利用关系研究
——利用有约束条件的似乎不相关回归模型分析
◎ 丁成日 牛 毅 何莲娜 李 智
摘 要:城市经济发展需要建筑空间作支撑,不同的经济活动有不同的建筑空间要求,而不同土地利用类型有不同的建筑容积率,因此为城市经济发展供给城市土地就比较复杂。产业与城市土地之间数量关系是实现经济规划与城市规划融合、经济规划“空间落地”的一个重要技术关键。本文利用有约束的似乎不相关模型分析经济产业与城市土地之间的关系,通过北京实证估算,该方法推算的结果比较符合实际。我们认为该方法可以广泛地应用到其它城市,在直接数据缺失的情况下,这个非调查方法的实用价值不可低估。
关键词:经济产业 城市土地利用 非住宅用地需求 似乎不相关回归模型 约束条件
根据中国规划法规,城市规划需要为市场经济服务。在法律地位上,基于宪法的城市经济和社会发展规划要高于城市总体规划和土地利用总体规划,处于主导地位,后两者不能与之相抵触(丁成日,2009)。在《城乡规划法》中,就要求城市总体规划以经济和社会发展规划为依据,与土地利用总体规划相衔接。这些都要求经济发展规划、城市总体规划和土地利用规划的融合,即“三规合一”(丁成日,2007)。
经济发展规划主要规划、预测经济和产业的发展规模、速度、结构等。城市总体规划的一项重要内容,是根据经济分析和预测结果,确定土地供给的总量、结构及其空间分布。因此,明确经济产业和城市用地之间的经济关系,是“城规”服务“经规”、使“经规”和“城规”融合的关键。经济发展与城市土地开发之间的联系是主要是通过就业来实现的,经济发展通常都与就业增长紧密相连(技术进步也能带来经济增长,但是经济发展或者萎缩一个重要指标是就业增长率)。由于就业人数不直接消费土地,而是通过消费建筑空间来间接地消费土地,因而经济发展与城市土地开发的关系就变得复杂。另外,不同经济产业对建筑空间的要求是不一样的。如制造业中自动化程度高的产业需要的建筑空间平面展开,而金融证券(总部)就业需要的建筑空间立体展开。一般地,商业办公用地的建筑容积率可以很高,而用于制造业的工业用地容积率一般都比较低。不同经济产业部门同等数量的就业增长所需求的土地利用类型和量都不同。可见,为实现经济规划与城市规划衔接和融合、经济规划空间落地的科学规划目的,首先需要解决的技术问题是如何根据经济发展(就业增长)量来决定相应的城市土地用地类型和量。解决这个问题需要利用经济产业与城市土地利用之间的数量关系。
中国城市目前还没有这样经济产业与城市土地利用类型相互匹配的详细数据。由于既缺乏数据,又没有相应的技术支持,中国城市规划主要是通过人均土地面积来供给城市发展①。丁成日等(2014)首次利用非调查方法来估计经济产业和城市土地利用之间的关系,方法是数学迭代-最小二乘法。本文发展了有约束条件的似乎不相关回归模型,来推算经济产业和城市土地利用关系。由于是非调查方法,没有真实的数据来佐证,故利用完全不同的方法来推算,以此来提高方法的可行度,这是基础应用研究惯例。 因而,本文是对丁成日等(2014)发展的方法的补充。
一、经济产业与城市土地的关系
城市经济分析和预测既涉及总量又涉及分经济产业部门,如制造业、交通运输、金融房地产、零售服务、政府管理等。城市规划和城市土地发展主要围绕五大土地利用类型:住宅、工业、商业、办公和基础设施②。一方面,城市经济与非住宅土地利用(工业、商业和办公)之间的关系非常密切,城市经济活动离不开土地;另一方面,两者关系非常复杂,同样的经济活动强度(就业量),不同经济产业有不同的城市土地利用类型和强度。第三产业基本上不需要工业用地,需要的主要是商业和办公(金融房地产业);而制造业的土地利用类型主要是工业用地。比如,美国克利夫兰郡制造业的就业人数的98.95%是在工业用地上,只有1.05%分布在办公用地;金融保险有78.75%的就业是在办公用地上,21.25%在零售用地;对建筑业而言,由于大量工人在户外/野外工作,只有一小部分就业需占用办公或工业用地,而大部分就业不产生土地需求(丁成日等,2014)。
不同产业占用的土地利用类型不同,同时不同土地利用类型的容积率也不同,故不同产业就业建筑密度不同。表1显示美国波特兰市产业就业与城市建筑面积的关系,从表1可知,不同行业的建筑空间需求是不一样的。比如,交通业每个就业要求的建筑面积是金融、保险和房地产业的9倍左右,而烟草业主要是野外作业,故每个就业要求的建筑面积为零。单位就业人数要求的建筑面积越大,说明建筑面积就业密度越低(建筑面积/就业);相反,单位就业人数上的建筑面积越小,建筑面积就业密度越高。金融、保险和房地产、机器制造、健康类服务业的建筑面积就业密度是最高的,而交通、造纸、批发、纺织等行业建筑面积就业密度是很低的,说明这些行业需要的土地面积也大。建筑面积就业密度和不同产业就业在不同土地利用类型上的分布,都反映了经济产业与城市土地利用之间的关系③。
城市经济产业与城市土地利用之间的数量关系非常重要。第一,它是城市规划能够根据市场发展安排城市土地供给的依据。比如,发展制造业需要安排工业用地(新增)并需要特别规划,一方面是因为工业用地规模相对较大,另一方面由于工业用地产生相对较大的负面外部性(环境污染、大型货车相关的交通安全问题等),使工业用地的选址和非工业用地转变为工业用地都受到许多限制和约束。如果发展第三产业,新增土地供给可能不需要,就业增长需要的建筑空间可以通过不同土地利用类型上的建筑空间之间的转变来满足,如住宅用地上的建筑空间可以转变为商业或办公用途,商业和办公之间的用途转变也是非常常见的。第二,它使城市规划能够根据未来经济发展预测和政策倾向预测城市土地供给(包括类型和强度),更重要的是能够通过城市土地供给方向指导经济发展和落实城市发展政策,如停止工业用地供给有助于产业结构向第三产业发展倾斜。第三,结合中国国情,它可以通过定量分析预测城市土地需求(非住宅用地),为城市规划决策提供科学依据。中国城市土地供给一般模式是按照人均法来规划城市土地发展,并自上向下地分解土地利用类型。这种人均法不仅缺少科学性、与市场发展脱节,同时又使城市土地供给中难以摆脱行政干预和主观人为因素、难以避免城市土地供给的随意性和不一致性④。第四,它为“三规合一”提供技术基础。“三规合一”的目的之一是落实经济发展规划的空间落地这个长期困扰中国城市规划的难题。产业与土地之间数量关系能够使城市规划落实经济发展(产业和强度)空间用地问题(用地类型和强度),从而使城市规划能够遵循市场发展规律,使土地利用效率与市场机制衔接(丁成日等,2014)。

表1 美国波特兰市单位就业人数的建筑面积(平方英尺/就业)
美国产业和土地之间的数量关系是根据调查数据统计汇总而得,而中国城市目前还没有地块上详细的产业和土地利用相互匹配数据。丁成日等(2014)利用数学迭代-最小二乘法估计了北京产业与土地利用之间的数量关系,本文应用有约束条件的似乎不相关分析模型来分析北京产业-土地之间的数量关系。由于北京经济结构以非农经济为主,且非农经济主要集中在城市核心区,故研究区是以北京六环为大致界限划定的(图1)。产业数据是分产业部门的就业人数,产业部门汇总为14个行业,分别是农业和采掘、轻纺食品、重化工、冶炼加工、设备制造通讯、其它制造业、建筑业、交通邮政信息、批发零售住餐、服务、金融房地产、科技教育、文体娱乐、和公共管理和社会组织。土地利用数据是4类土地利用类型,分别是工业、商业、办公、和其它(体育、医疗卫生、教育科研、和对外交通)⑤。数据是按照1平方千米格网组织的,故每个格网的数据包括分14个经济行业的就业人数,以及4类土地利用的建筑面积、土地面积和容积率。2592个网格中有473个网格有非住宅土地利用类型,但是就业数据为零,主要分布在五至六环。这些网格可能因为正在发展建设等原因,尚没有就业,故在分析模型中不予考虑,这样整个分析所利用的网格为2119个。

图1 北京六环以内的1平方千米网格
二、似乎不相关回归模型
由于产业就业直接消费的是建筑面积,而不是土地面积,同时在其它条件不变的假设下,行业就业人数增加,建筑面积也需要增加,即行业就业与建筑空间有着正的相关关系。根据该理论基础,构建回归分析模型如下:


方程的数量为G,Xg的维度是1×Kg,βg的维度是Kg×1。我们也可以写成如下形式:
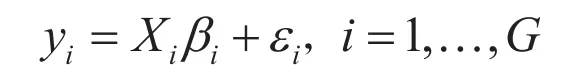
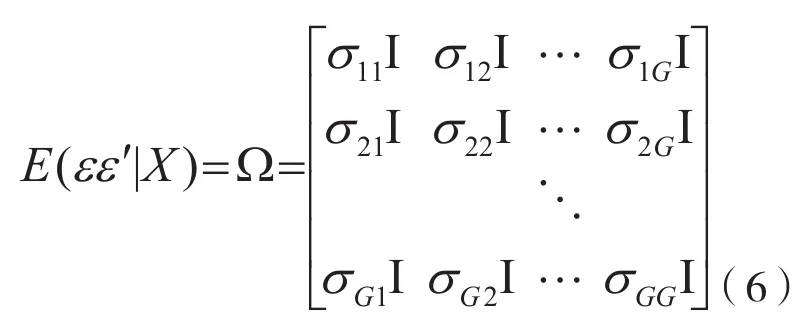
这是一个行数和列数均为G×N的方形矩阵,维度是(G×N)×(G×N)。在这种情况下,只要各方程的自变量不尽相同,OLS估计就因为没有考虑方程间的相关关系而不是有效(Efficient)的,需要使用似乎不相关回归。
此外,根据研究需要,可以对似乎不相关回归分析模型设置约束条件。设置约束条件有两种方法。第一种是对单个参数设置约束条件。对特定研究对象,回归参数不应该是任何值,而是需要被限定在一定范围,比如必需大于零,或者取值范围在(0,1)以内。第二种是有多个估计参数构成约束条件。最普遍的是“加总限制”(adding-up constraint),即几个估计参数之和满足一个约束条件。例如,如果要求方程组(5)中,则可以设定,方程组中第G个方程变为。这种约束条件要求对非线性方程组同时进行回归估计,即非线性似乎不相关回归(Nonlinear Seemingly Unrelated Regressions, NSUR)。需要指出,“加总限制”既可以对同一个回归方程内不同自变量参数设置,也可以对同方程组内同一个自变量参数设置。本文的“加总限制”是同一个自变量在式(1)-(4)中4个不同的估计参数设置约束,技术上难度较大,属于高级计量经济研究的范畴。
根据Zellner(1962)和Telser(1964)的研究成果,对方程间有相关关系的似乎不相关回归进行一致又有效的一种估计方法是广义最小二乘法(Generalized Least Squares,GLS)。在实际运用中,方程组的残差矩阵是未知的,因此在进行GLS估计时,就需要先用OLS的方程残差来估计出方程组的残差矩阵,然后再根据GLS的步骤估计β。这种方法称为可执行的广义最小二乘法(Feasible Generalized Least Squares,FGLS)。
对有约束条件的似乎不相关回归模型进行估计的一种方法是两步可执行的广义最小二乘法(Two-step Feasible Generalized Least Squares, Two-step FGLS)。该方法与线性SUR的FGLS相似,需要先对各个方程分别进行单独的非线性最小二乘估计(Nonlinear Least Squares),得出残差向量。然后估计出方程组的残差矩阵,然后根据残差平方和最小化估计出系数矩阵β。本文利用两步可执行的广义最小二乘法来估计方程(1)-(4)。
三、北京产业与土地关系回归估计
1.估计方程及其约束。利用方程组(1)-(4)来估计产业与城市土地之间的数量关系时,需要特别注意两个问题。第一,正如前文所述,产业与土地之间的逻辑关系需要给予充分考虑。有些产业对不同土地利用类型的需求是不一样的,比如,第三产业没有工业用地需求。因而,方程组(1)-(4)的自变量不尽相同。每个方程自变量的选取不仅反映产业和土地的逻辑关系,同时也会使似乎不相关回归模型得到最有效的估计结果。
根据理论和北京发展特点,我们认为表2能够反映北京产业与城市土地利用关系。表中的“强”说明产业与土地利用关系密切,“无”说明两者基本没有关系,如制造业的就业主要落在工业用地上,对文化体育、卫生医疗、教育科研和对外交通用地基本没有需求。表2中的空白说明有几种可能:一是我们对两者的关系不确定,故需要通过模型和统计分析来确定;二是两者关系弱小,或者可能是没有的。表2即指导方程组(1)-(4)的自变量选取,可以为解读回归方程估计参数提供参照。比如,工业建筑面积方程只有10个产业就业变量,4个没有包括的变量是金融房地产、科技教育、文体娱乐、和公共管理与社会组织;而办公和商业方程都是14个产业就业自变量。这种自变量选择实际上等于把相应的回归参数设置为零。
第二,设置约束条件。有两个约束条件,第一个约束条件是所有的回归参数都不能小于零,即,其中t代表产业类型,j代表用地类型。原因很简单,如果回归参数小于零,这意味着每增加一个就业人数,相应的建筑面积需求将减少,这显然不符合城市发展的基本逻辑。第二个约束条件是不同土地利用上的就业之和不能超过总就业。假设行业1在一个格网内的总就业人数为100人,这些就业人数被分配到工业、商业、办公和其它土地利用类型,因而这四个土地利用类型上行业1的就业人数之和不能超过100人,但是可以小于100人,因为有些行业中的人员是在野外作业,不需要建筑空间,如建筑业。
数量关系上,这个约束条件表达为:

其中,R代表各用地类型的就业密度(建筑面积/就业)。这样,反映办公用地上的t行业的就业人数。由于R值不知道,可以另外估计、推算。也可以在土地需求方程组中对R和进行统一估计,这需要假设不同产业在同一类用地上的就业密度都是一样的,然后将式(1)-(4)改写成如下形式,加上系数大等于零的约束条件和约束条件(7),进行参数估计:


表2 北京产业与土地利用理论或期待关系
2.初步估计结果。为便于对比,首先利用最小二乘法对方程组(1)-(4)进行单独估计。我们发现,当不设置任何约束条件时,会出现一些估计值为负的系数,显然与现实不符。当设置系数大于零的约束条件后,结果与预期更接近。办公用地的需求基本不受农业与采掘业以及各类制造业发展的影响,而主要受建筑业、各种服务业和政府公共部门就业的影响;需要工业用地的则主要是制造业,以及农业与采掘业; 影响商业用地需求的包括农业与采掘业,部分制造业,以及各种商业服务业;影响其他用地的是文体娱乐、科技教育和政府部门⑥。我们根据这些初步回归结果和表2,选择了模型的自变量,对方程组(1)-(4)进行系数大于零的似乎不相关回归。
表3显示似乎不相关回归模型结果。该表说明,前5个行业,即农业与采掘业以及所有制造业(其他制造业除外),主要产生的是对工业用地的需求,而对办公和商业用地的需求不明显。这5个行业增加1单位就业,分别会增加工业用地建筑面积4.35、15.30、16.77、22.26和20.55平方米。建筑业、交通通信、批发零售住餐、服务和金融房地产对办公和商业用地均有显著的需求。文体娱乐、科技教育和公共管理社会组织3个行业对办公和其他用地均有显著的需求。对办公用地影响显著的是文体娱乐和公共管理社会组织,每增加1单位就业会分别增加13.75和5.16平米建筑面积。对商业用地影响显著的是服务、批发零售住餐、金融房地产,每增加1单位就业会分别增加19.7、9.19、7.61平米建筑面积。对其他用地影响显著的是科技教育,每增加1单位就业会带来15.99平米建筑面积的需求。

表3 系数大于零的似乎不相关回归结果
3.最终估计结果。上述结果可以估计出各行业就业的边际土地需求,但尚不能估算出各行业就业在不同用地类型上的百分比分布。要达到此目的,需要估计出各类用地的就业密度,即每单位就业占用多少建筑面积,并假设同类土地利用上的就业密度相同。这一假设也是应用方程间约束的一个前提条件。
对方程组(1)-(4)加约束条件(7)的估计需要知道不同土地利用类型上单位就业人数的建筑面积(就业建筑密度R值)。一种计算R值的方法是将总就业对各类用地建筑面积进行回归,得到总就业和土地利用的对应关系,即当其他用地面积不变时,增加一平米某一类用地建筑面积会相应增加多少就业,从而推算各类用地的就业密度。结果如表4所示,办公用地的就业密度最高,每个工作岗位占用8.9平米建筑面积;工业用地的建筑面积最低,人均46.4平方米;商业和其他用地的人均面积为14.5和21.9平方米。
根据这些就业密度估计值和表3,可以计算出各行业就业在各类用地上的百分比分布情况(表5)。具体是,根据表3中一个行业平均每个就业占用一种用地类型的建筑面积,除以表4中该用地的人均建筑面积,即为该行业就业分布在该用地类型上的比重。例如,表3显示,建筑业每增加100人就业,会增加343平方米办公用地和89平方米商业用地的建筑面积。如果按照表4,办公用地上的就业每人占用8.9平米,商业用地上每人占用14.5平米,那么可以推算建筑业新增就业有38.39%分布在了办公用地上,有6.11%分布在商业用地上,有55.5%很可能露天作业。由表5可见,通过表3计算的产业—土地关系式,很多产业在不同土地利用类型上的就业之和或者大于100%,或者小于100%。这显然不符合现实。
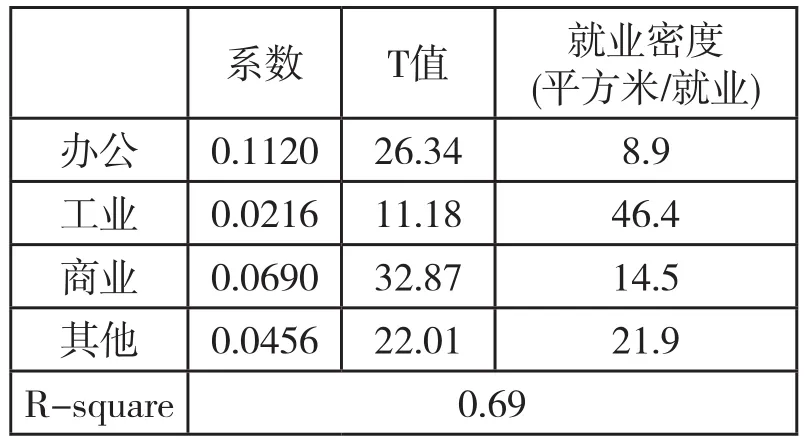
表4 对各类用地人均建筑面积的估算

表5 各行业就业的在用地上的分布(基于表3和表4)
一个产业就业在各类用地上的分布比重加总应不超过100%。为满足这一约束条件,我们将土地需求方程组写成(8)~(11)的形式,并增加方程间约束条件(7),进行SUR估计。估计结果如表6和表7所示。与表3相比,在表6中,大部分行业的办公用地需求有所增加,而工业、商业用地需求趋于近似。估计出的办公、工业、商业和其他用地的人均建筑面积分别为12.51、19.36、11.47和15.85平方米。
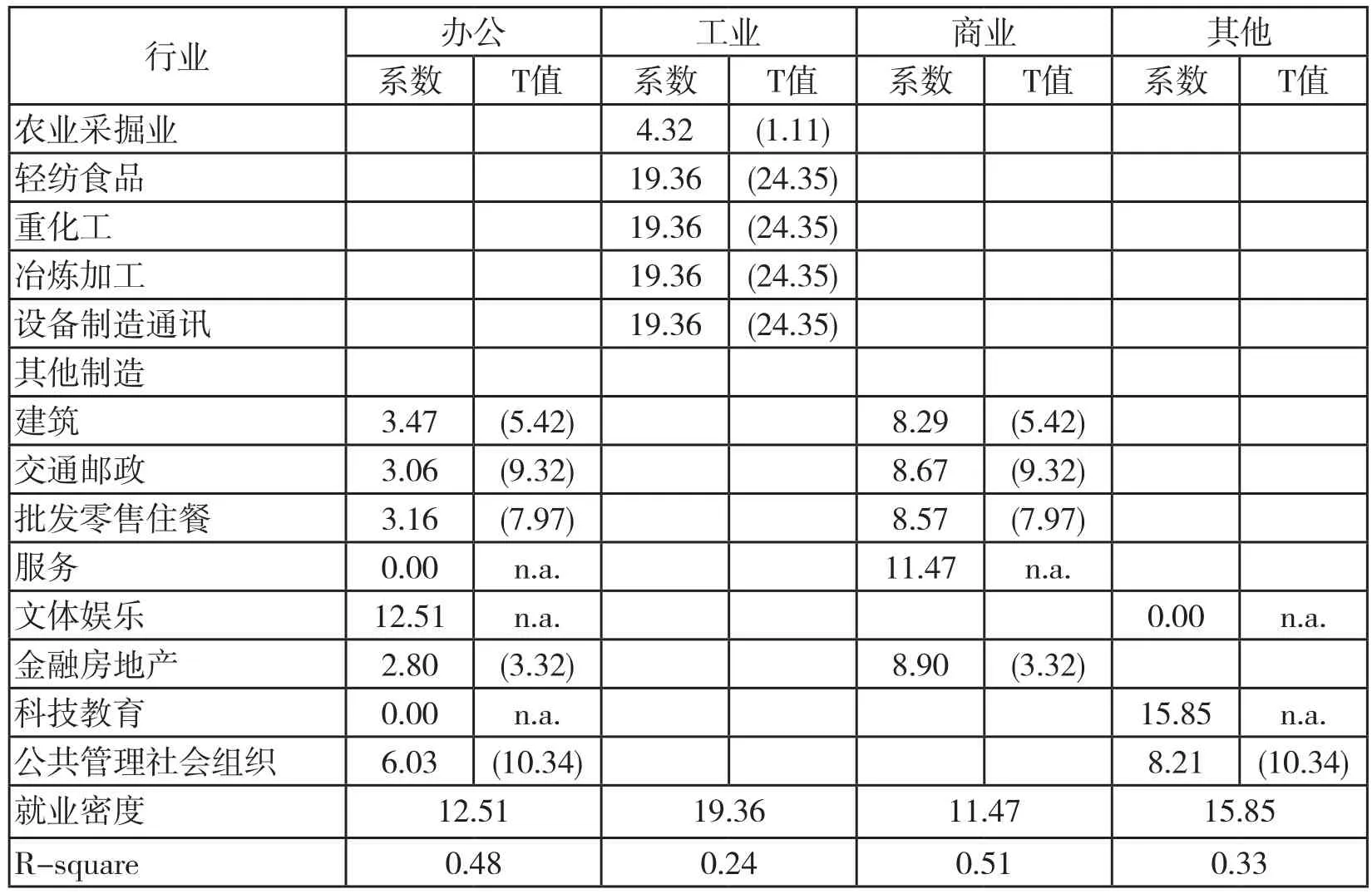
表6 约束添加的似乎不相关回归估计结果
表7是根据表6的估计参数计算而得(具体计算方法同前)。表7同表5相比,各行业的就业份额加总均为100%,只有农业和采掘业、建筑业例外,前者有22.33%的就业利用工业用地,后者有27.7%和13.53%的就业利用办公用地,而这是我们期望的。与不加方程间约束的就业分布(表5)相比,加方程间约束的就业分布(表7)有如下几点改变。第一,大部分行业的就业比重加总等于100%,只有存在露天作业的农业采掘业和建筑业的加总才会小于100%,与现实情况基本一致。第二,各个比重系数均在0-100%之间,不再出现大于100%的不符合现实的情况。第三,少数行业的就业分布有明显改变,如服务业不再占用办公用地,文体娱乐不再占用其他用地,可能与行业分类、用地分类有关。
四、结语
本文利用有约束条件的似乎不相关回归模型,分析北京产业与城市土地利用之间的关系。通过北京的案例分析说明,在没有调查数据的基础上,通过现有的数据,利用非调查方法是可以建立产业发展与城市土地利用之间的关系的。回归分析表明,产业与土地利用关系符合直观的判断,基本能够反映北京城市发展现状。本文的方法可以在其它城市推广,故应用价值是不可低估的。
由于数据和时间有限,本文的分析结果有一定的局限性。这主要是城市土地利用分类不够细,有些城市土地利用在中国城市是非常典型且相当普遍,比如,混合土地利用。还有,城市基础设施和公共用地(如高等教育、文化体育等)可能需要特殊处理。它们的特殊性可能需要不同的分析模型来推算,而不是同其他土地利用类型一并分析。

表7 各行业就业的在用地上的分布(基于表6)
本文在方法上与丁成日等(2014)不同,计算的经济发展与城市土地利用数量关系也有所区别。丁成日等(2014)利用数学迭代-最小二乘法推算的是平均关系,而本文利用有约束的似乎不相关回归模型推算的是边界值。从根据优化理论,短期内,城市土地利用优化时,土地利用的均值和边界值应该是相等的。因而,本文的方法与丁成日等(2014)的方法既相互补充,可以间接地用来判断城市土地是否是优化的:当均值与边界值相等时,土地利用是优化的,否则两者差别越大,说明城市土地利用越偏离最优值。
中国的城市规划长期侧重于形态和设计,定量分析和模型技术对规划的决策支持非常有限。造成这种现象的原因很多,通过本文的模型分析说明,科学储备和基础研究不足也是一个重要的原因。经济规划和城市规划融合,“三规合一”等需要技术上的支持。如果没有技术上的支持,这些很可能成为空洞的术语和概念,难以具体地指导城市规划和管理。
注释:
①人均土地需求法的弊端及其评价见丁成日等(2014)。
②这里基础设施包括城市公共空间和绿地。
③在平均值上,两者可以互相推导,即知道一个表即可推算出另外一个。
④有关城市土地供给的人均法问题见丁成日等(2014)。
⑤市政公用设施类型没有包括在内,原因是一个地点上这些设施可能与该地的相关就业没有联系,而与城市相关部门的总就业有关。
⑥其他制造业占用土地极少,可能占其主要部分的水、电、燃气的生产制造占用了市政用地而非工业用地。因该行业规模较小,不再专门讨论。这些初步回归结果因篇幅所限,没有列出,如读者需要可以联系作者。
参考文献:
[1]丁成日. 城乡规划法对城市总体规划的挑战及其对策[J].城市规划,2009,2:50-55.
[2]丁成日.“经规”、“土规”、“城规”规划整合的理论与方法[J].规划师,2009,3:53-58.
[3]丁成日. 城市空间规划:理论、方法与实践[M].北京:高等教育出版社,2007.
[4]Wooldridge, J. Econometric Analysis of Cross Section and Panel Data [M]. The MIT Press, 2010.
[5]Zellner, A. Estimators for Seemingly Unrelated Regression and Test of Aggregation Bias [J]. Journal of the American Statistical Association, 1962, 57: 500-509.
[6]Telser, L. Iterative Estimation of A Set of Linear Regression Equations [J]. Journal of the American Statistical Association, 1964, 59: 845-862.
[7]Yee, Dennis and Jennifer Bradford. Technical Report—1999 Employment Density Study, 1999, Metro (http://library.oregonmetro.gov/files/1999employmentdensitystudy.pdf).
(责任编辑:李钧)
Applying Seemingly Unrelated Regression with Constraints to Estimate the Relationship between Economic Sectors and Urban Land Uses
Ding Chengri, Niu Yi, He Lianna, Li Zhi
Abstract:The relationship between economic sectors and urban land uses is critical to estimate land demand based on market development. This paper develops a Seemingly Unrelated Regression Model with Constraints to estimate the relationship. Empirical analysis using Beijing Data reveals that estimated coefficients are consistent with expectation in terms of significant levels and magnitude in size. It is concluded that this non-survey method can be applied to many other Chinese cities to overcome non-availability of survey data to establish the relationship.
Keyword:economic sectors; urban land uses; non-residential land demand; seemingly unrelated regression; constraints
【中图分类号】F293.2
doi:10.3969/j.issn.1674-7178.2016.02.007
作者简介:丁成日,博士,马里兰大学城市理性增长国家研究中心教授(终身),首都经贸大学讲座教授,主要研究方向为城市经济学、城市政策、土地政策、城市规划、城市管理、政策和规划分析等;牛毅,博士,首都经济贸易大学国际经济管理学院助理教授,硕士生导师,主要研究方向为城市经济学、住房、公共财政、城市规划、应用计量;何莲娜,北京市城市规划设计研究院高级工程师; 李智,马里兰大学城市研究与规划系博士研究生。

