近年高考数列题中不等式放缩的几个常用模型
2016-07-08 09:09浙江省绍兴市鲁迅中学虞关寿陈少春邮编312000
中学数学教学 2016年3期
浙江省绍兴市鲁迅中学 虞关寿 陈少春 (邮编:312000)
近年高考数列题中不等式放缩的几个常用模型
浙江省绍兴市鲁迅中学虞关寿陈少春(邮编:312000)
数列是高中数学学习的重要知识内容,是初等数学与高等数学的重要衔接点,它在历年的高考解答题中都占有相当重要的地位.把数列与不等式结合起来历来是高考命题的热点.处理这类问题是我们不得不面临的.我们知道数列是特殊的函数,处理数列与不等式问题可以参考函数与不等式的处理方式,但数列又属于离散数学范畴,所以处理这类问题又不能照搬函数与不等式的处理方式,它具有它的特点.本文想通过近几年高考与各地高考模拟题中,考查数列与不等式所呈现出的方式,探析数列与不等式问题中不等式放缩的几个常用模型.
在解决数列和不等式的有关问题时,常用这个不等式模型达到放缩目的,具体又表现在下列几种情况:

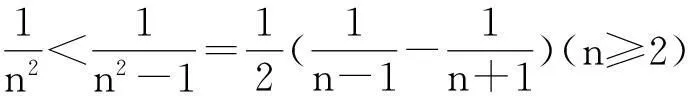
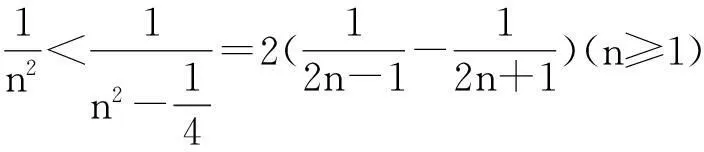
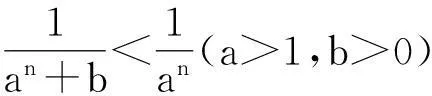

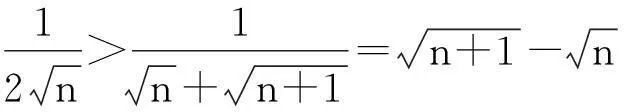
(2)证明:对一切正整数n,有
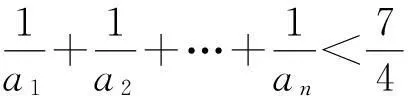


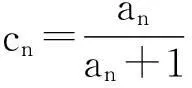

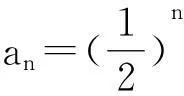
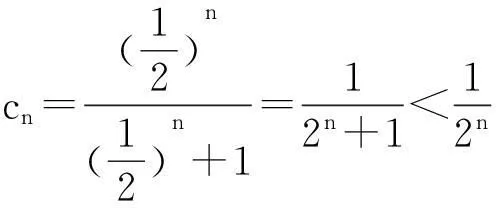

(2)试找整数M,使M 3利用一个不等式的恒成立问题 (1)求a1的值; 解析(1)可求出a1=1,a2=5; (2)由题设条件可知当n≥2时,2Sn=an+1-2n+1+1,2Sn-1=an-2n+1两式相减得:an+1=3an+2n(n≥2),即an+1+2n+1=3(an+2n),则{an+2n}是从第2项起以3为公比的等比数列,从而an+2n=(a2+22)·3n-2=3n,即an=3n-2n(n≥2),又a1=1也满足上式,故an=3n-2n(n∈N*); (收稿日期:2016-03-10)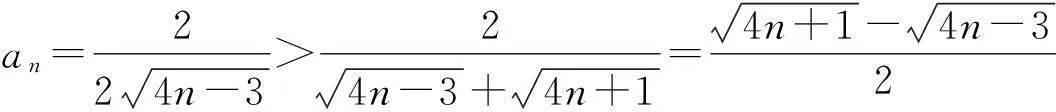





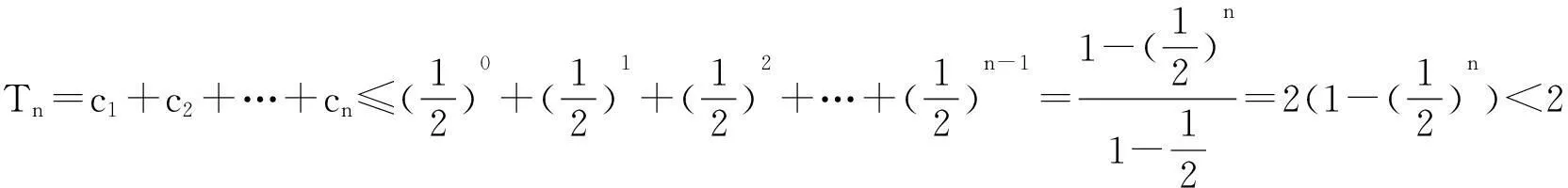
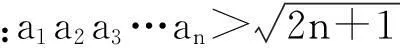
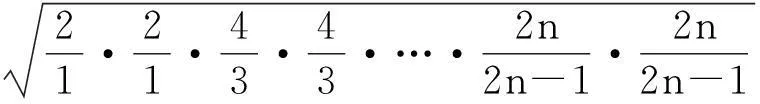

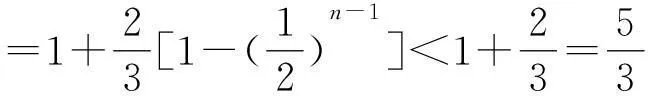
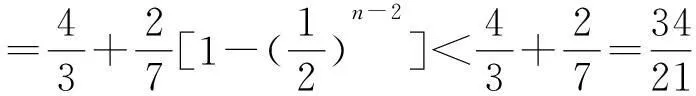
猜你喜欢
老年教育(老年大学)(2022年8期)2022-08-24
小学生作文(低年级适用)(2021年5期)2021-05-24
新农村(浙江)(2021年3期)2021-03-08
音乐天地(音乐创作版)(2020年12期)2020-12-06
非公有制企业党建(2020年8期)2020-08-26
浙江国土资源(2019年10期)2019-10-31
人物画报(2019年2期)2019-09-10
中等数学(2018年7期)2018-11-10
中等数学(2018年4期)2018-08-01
中华建设(2017年2期)2017-06-01

