法之不同 品有所异
河北省丰宁满族自治县第三中学 吕振杰 (邮编:068050)
解题
法之不同品有所异
河北省丰宁满族自治县第三中学吕振杰(邮编:068050)
解题是数学学习中最主要的活动.波利亚说过:数学就是解题,并提出问题.然而对于同一个问题,采取不同的策略处理,往往获得不同的数学训练效能,展示不同的思维精彩.教学、复习中,如何实现“法之不同,品有所异”的效果,应该成为教师教学的追求和境界.下面以题目:“若关于x的不等式acos2x+cosx≥-1恒成立,求实数a的取值范围”为例,进行阐释.
1通法万能 培养习惯
通法是一切方法的基础,高考一般是在通法、基本方法上进行考查,没有通法的熟练,就不会有巧法和妙法的悟道,更不可能有奇法的奇思妙解.一些重要的通法,学生应该牢固掌握,让通法成为解题的“利器”.
对于这个题目,观察题目中有cos2x和cosx,想到它们之间的关系是cos2x=2cos2x-1.这样原来的不等式变为a(2cos2x-1)+cosx+1≥0,就出现了“二次函数”的类型.设cosx=t,则变为:2at2+t-a+1≥0,其中-1≤t≤1.这样问题就变为当-1≤t≤1时,不等式2at2+t-a+1≥0恒成立,求a的取值范围.
记f(t)=2at2+t-a+1,其中-1≤t≤1.
(1)当a=0时,函数f(t)=t+1是一次函数,因为-1≤t≤1,所以f(t)=t+1≥0显然成立.





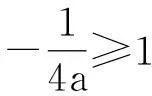
上述解法尽管过程冗长,却是解题的通法,是一般学生都应该会的解法,这种方法的价值,在于思维起步较低,容易上手,而解题过程中用到分类、数形结合的思想方法是必须要求学生掌握的,也是教学中必须加以强化和训练的,要时时注重与高考考法接轨.而在解题过程中较大运算量,正是要解决目前学生计算能力偏低的问题,现在学生有一个通病就是一看就会,一做就错,眼高手低,而这样的解题训练就是要培养学生的耐心和解题毅力,这一品质习惯的形成是高考解决解析几何题必须具备的素养,平时教学中要通过系统的训练培养学生通法上手,咬定解题不放松的品质.绝不能在奇、特、巧上过分追求,梳理出各部分知识结构中的通法、基本和根本的方法.





故an=3+2(n-1)=2n+1 .
2巧法简洁培养优化
训练学生的解题的简洁性,迅速性,缩短学生解题时间,优化解题路径,是数学教学的重要任务.解题中通法解答后,应该引导学生再思考,还有巧法吗?也就是我们经常说的一题多解,而这里追求的多法,要聚焦到“巧”上.巧法的关键在于对问题的变通——巧变形、巧构图、巧迁移,关键思维点的启动以及数学知识的迁移和重构.
上述题目如果训练到此结束,未免有些遗憾,鼓励学生展开自己的思考力,探究一下其妙法,少费时、伤神.因为 acos2x+cosx≥-1⟺a(2cos2x-1)≥-1-cosx,而-2≤-1-cosx≤0,因为对于任意 x∈R,a(2cos2x-1)≥-1-cosx恒成立.
(1)当2cos2x-1≥0,要使a(2cos2x-1)≥-1-cosx恒成立,必须使a≥0.

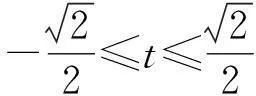



例2(2014年四川高考)平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角,等于c与b的夹角,则m等于()
A.-2B.-1C.1D.2
解答本题用纯代数法可以解答,但是计算较为繁琐.


3奇法制胜培养创新
出奇制胜,秒杀难题,于数学天地间驰骋,于解题突围中求创新,这就是数学更高、更远、更强的奥林匹克精神.这样坚持有助于培养学生创新意识和创新能力.而奇法、妙法的生成不是一蹴而就,需要不断的积累,且具有批判意识和挑战意识,最后才能融会贯通知识.“奇法”的关键在于突破固有思维模式的禁锢,在一般中找特点,在抽象中寻直观,在看似不相关中建相关,不走模式化思维.
对于本题,因为“关于x的不等式acos2x+cosx≥-1恒成立”,也就是a(2cos2x-1)≥-1-cosx恒成立.
(1)因为任意x不等式成立,所以令cosx+1=0,得到a≥0.



本题解法有三奇:奇在特值的应用;奇在变量换元为非负数;奇在变换成等价形式后,用基本不等式.


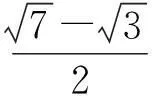

解答本题用代数法完成几乎不可能,
用构造法可以出奇制胜.

下面构造图形求解.


(收稿日期:2016-02-27)
方法

