多载波FTN系统脉冲成形滤波器的分析与设计* 1

段　昊，高媛媛，郭明喜，周智勇，聂晟昱，徐　洋

(1.解放军理工大学 通信工程学院研究生3队，江苏 南京 210007； 2.解放军理工大学 通信工程学院，江苏 南京 210007)



多载波FTN系统脉冲成形滤波器的分析与设计* 1

段昊1，高媛媛2，郭明喜2，周智勇1，聂晟昱1，徐洋1

(1.解放军理工大学 通信工程学院研究生3队，江苏 南京 210007； 2.解放军理工大学 通信工程学院，江苏 南京 210007)

摘要：多载波FTN (faster-than-Nyquist)系统会同时引入码间串扰和载波间串扰，增加了IFFT模块的实现难度。映射原理的提出很好地解决了这一问题，但同时也对成形滤波器的设计提出的更多要求。基于OFDM/OQAM系统，对多种原型滤波器的FTN映射性能进行了分析。为有效评价映射精度，推导并定义了误差能量的概念。基于多载波FTN信号的离散时间表达，进一步设计了一种基于高斯脉冲的优化数字滤波器。该滤波器满足严格的离散正交条件，且误差能量更小，映射精度更高，从而提高系统的误码性能。同时也降低了复杂度，有利于多载波FTN系统的硬件实现。

关键词：多载波FTN；成形滤波器；映射模块；误差能量；复杂度

0引言

实现数据的可靠、高效传输一直是通信发展的主要目标，众所周知，通信系统中码元的传输必须遵循Nyquist速率准则，否则会引起码间串扰，影响误码性能。为了进一步提高频带利用率，Mazo等人在1975年提出了FTN(faster than Nyquist)传输技术，指出码元传输可以在一定限度内超过Nyquist速率，不影响系统误码率，我们称之为Mazo限[1-2]。这一原理的提出也为发展多种高速传输技术提供了新的思路。近年来，以OFDM为代表的多载波通信技术得到了广泛的应用[3]，与传统的单载波通信相比，该技术在抗干扰性和高效传输等方面拥有诸多优势，将FTN的概念引入到多载波通信领域有着实际的应用价值。

2005年，Rusek等人首次将FTN原理与多载波技术相结合，提出了二维Mazo限的原理[4]，指出信号可以在时域和频域同时进行一定程度的压缩，不会影响误码性能。以此为基础，他们又提出了多流FTN的概念[5]，从理论层面上证明了多载波FTN技术的可行性。针对多载波FTN系统的具体实现方案，文献[6]进行了进一步的研究，首次提出了映射模块的概念，将FTN信号等效转化为普通的OFDM/OQAM正交符号，简化了系统设计的复杂度，但同时也提高了成形滤波器的设计要求。文献[7]比较了矩形窗和IOTA(isotropic orthogonal transform algorithm)函数作为成形脉冲时的映射性能，可以看出IOTA滤波器明显更加适用于多载波FTN映射模块。但是，考虑到IOTA滤波器自身的运算量，映射模块精度的提高实际上是以高复杂度为代价的。研究表明，除了IOTA，还有多种时频聚焦性能(TFL，time frequency localization)性能优异的滤波器能够适用于OFDM/OQAM系统[8-9]，这些脉冲的映射性能有待进一步研究。另一方面，分析过程中并没有给出映射精度的具体量化标准。在实际滤波器设计时，往往采用优化的数字滤波器，而映射系数的内积运算，本质上建立在对连续脉冲进行采样和截断的基础上的。因此，设计合适的数字滤波器，从而提高映射精度、降低模块复杂度，是一个值得研究的方向。本文着重研究了多载波FTN脉冲成形滤波器的分析和设计方案，具体的工作和章节安排如下：

(1)第一部分给出了对基于OFDM/OQAM的多载波FTN系统模型，映射模块原理进行了分析。

(2)第二部分定义了误差能量的概念，全面分析了多种经典原型滤波器的映射性能。

(3)第三部分基于离散时间下多载波FTN系统，设计了一种基于DZT(discrete Zak transform)变换的改进高斯滤波器。

(4)第四部分进行了仿真和数据分析

(5)第五部分对全文进行了总结。

1系统描述和模型分析

1.1基于OFDM/OQAM的多载波FTN系统

OFDM/OQAM系统，顾名思义，即采用偏置正交幅度调制(OQAM)的一种OFDM系统。与传统的一些多载波实现方式不同，该系统将QAM调制后的复数信号实部和虚部分开，交替延时半个周期后分别进行传输，而各子载波间也并不要求严格正交，只需满足实数域正交条件。基于OFDM/OQAM的多载波FTN信号需要在时频域同时进行压缩，系统格点分布如图1所示。

图1　多载波FTN系统时频域示意

在图1中，黑色格点代表未压缩前的OFDM/OQAM符号，称之为正交符号，交叉格点表示压缩后的非正交FTN符号。需要指出的是，本文中所有“正交”均指实数域正交。多载波FTN系统发送信号可表示为[7]：

(1)

这里ak,l即为发送的实数符号(取值为±1)，k、l是相应的时频序数，TΔ、FΔ即为时频域的压缩系数。T0是传统OFDM系统中复数符号的传输周期，K表示子载波的数目，本文假定其为偶数，即K=2N(N∈Z+)。g(t)代表高斯脉冲，考虑到其具有优异的TFL特性本文将其作为FTN信号脉冲。

1.2发送端映射模块

众所周知，多载波系统通常采用IFFT模块以降低系统复杂度，但是经过时频压缩之后，IFFT的实现难度显著增加。基于映射模块的实现方案能够很好地解决这一问题[7]，图2和图3分别给出了基于映射原理的系统框图和映射格点示意图。

(a)基于FTN映射模块的系统发送端框

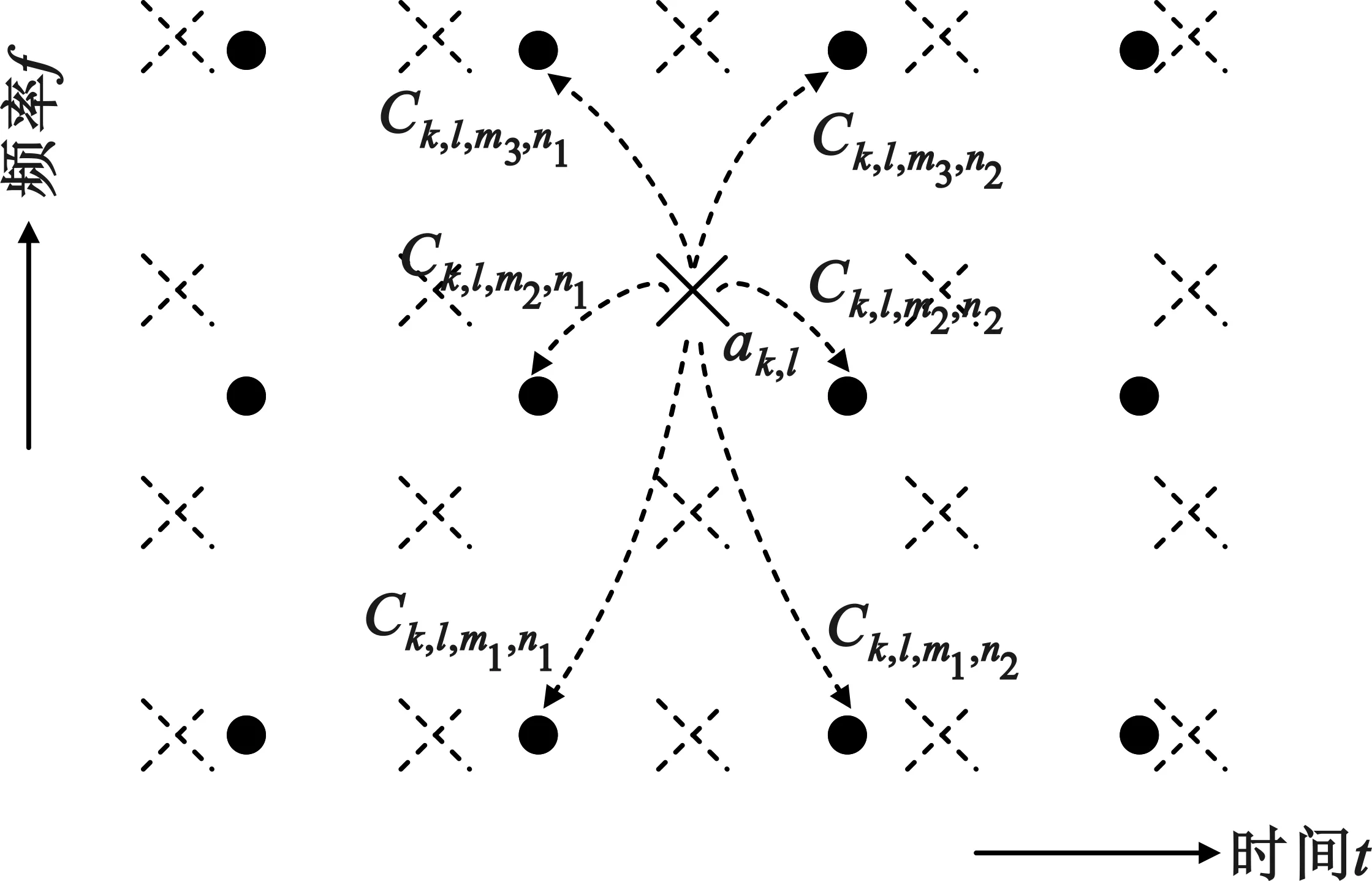
(b)多载波FTN格点映射示意

(2)

这里Ck,l,m,n即为映射系数，其基本原理如图2(b)所示，可以表示为：

Ck,l,m,n=R〈gk,l(t),ψm,n(t)〉

(3)

(4)

(5)

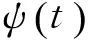
2原型滤波器映射性能分析

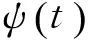
2.1映射精度评价参数

(6)

产生的误差函数定义为：

(7)

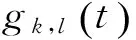
(8)

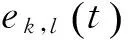
(9)

因此，我们可以得到映射过程中误差能量为：

(10)

式中，εs代表信号的能量，这里我们对滤波器脉冲能量归一化处理，可得：

(11)

误差能量可以用以衡量映射精度，它实际上反映的是重构信号相对于原信号的有效能量损失程度。显然，误差能量值越小，映射精度越高。当然，评判映射模块的性能，并不能仅仅依据误差能量，还要考虑不同脉冲下映射系数的计算复杂度。而这两个参量也正是本文用以衡量映射模块性能主要标准。

2.2原型滤波器

设计合适的成形滤波器是提高映射模块性能的核心问题。因此，下面我们对几种经典的OFDM/OQAM原型滤波器进行映射性能分析。

(1)平方根升余弦脉冲(RRC)[10]

平方根升余弦函数是一种经典的原型脉冲，广泛应用于现有的各类通信系统中。该滤波器表达式如下：

(12)

这里我们采用α=0.3的RRC脉冲。

(2)扩展高斯函数(EGF)[8]

扩展高斯函数(EGF)是基于高斯函数的改进脉冲方案，既具有良好的时频聚焦特性，也满足实数域正交的要求，其时域表达式如下：

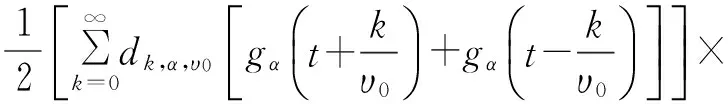
(13)

式中，gα(t)=(2α)1/4e-παt2(α>0)，即高斯函数，其系数dk,α,υ0均为实数，可以被精确计算[8]。υ0、τ0分别是时频域间隔参量，满足υ0τ0=1/2。根据本文采用的OFDM/OQAM模型，我们规定α=1，τ0=T0/2，υ0=F0=1/T0。

(3)各项同性正交变换函数(IOTA)

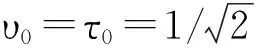
2.3映射性能分析

图3给出了三种原型滤波器的映射重构脉冲与原高斯脉冲的对比情况。从映射精度的角度来看，可以发现EGF脉冲性能最优，实际上，通过本文第四部分的能量误差数值分析可以发现，在映射精度性能方面，EGF脉冲>IOTA脉冲>RRC脉冲，这是因为RRC的TFL性能最差，在映射的过程中难以实现能量的集中，因此误差能量较高。而EGF虽然比IOTA的TFL性能略差，但采用了与系统模型相匹配的参量，反而取得了更高的映射精度。从复杂度角度来看，对单个FTN符号的映射运算量进行分析，可以发现RRC脉冲的运算复杂度最低，其他两种脉冲复杂度相当。

(a)RRC映射重构脉冲

(b)EGF映射重构脉冲

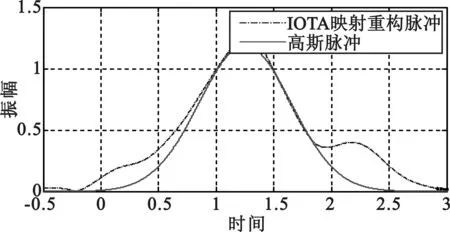
(c)IOTA映射重构脉冲

总的来讲，三种滤波器各有特点，EGF函数良好的映射精度也是以复杂度的提高为代价的。实际上，映射精度的计算都是建立在连续脉冲截短和抽样的基础之上的，这样的处理显然会牺牲一定的正交性，而密集的采样也增加的计算复杂度。因此，我们考虑设计一种离散条件下严格正交的数字滤波器，兼具良好映射精度和复杂度性能。表1给出了三种滤波器各项性能的分析与对比，其中N代表仿真计算时脉冲采样点的个数，仿真模型将在第四部分详细介绍。

表1　三种原型脉冲映射性能对比

3数字滤波器设计方案

3.1多载波FTN信号的离散时间表达

考虑到OFDM/OQAM系统在周期T0时间内传输了K=2N个复数信号，设定抽样时间为Ts=T0/2N，假设滤波器p[v]长度为L，那么需要在区间[-(L-1)/2Ts,(L-1)/2Ts]范围内对p(t)进行抽样，时延为(L-1)/2Ts，可以得到常规OFDM/OQAM离散信号的表达式[11]：

(14)

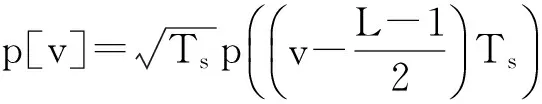
(15)

在此基础上，我们可以进一步得到离散时间的多载波FTN表达式，同样地，基于离散高斯脉冲g(v)，可以得到：

(16)

为了确保时延的精确性，我们规定TΔ=i/N(i=1,2,…,N)。则相应的FTN基函数为：

(17)

另一方面，我们将离散基函数ψm,n[v]和gk,l[v]代入到1.2节误差能量的推导过程中，假设Ck,l,m,n=〈gk,l(v),ψm,n(v)〉，将积分等效为叠加，很容易能够发现，离散系统映射精度的计算仍然可以沿用式(10)。

3.2基于高斯脉冲的正交滤波器设计

文献[12]根据DTZT变换(discrete-timeZaktransform)，提出了时频局域优化脉冲的正交条件。在此基础上，我们采用DZT变换(discreteZaktransform)的方法，提出了一种改进的高斯脉冲数字正交滤波器。该滤波器应用于多载波FTN系统后，不仅能够获得时频的正交性，而且可以保证优良的TFL特性，从而进一步地提高了映射精度，也降低了模块复杂度。

首先，我们给出DZT变换条件下滤波器p0[v]的正交条件：

(18)

这里R是任意取定的常数参量，Zp0[v,u]即为有限长脉冲p0[v]的DZT变换，其表达式如下：

(19)

式中，v=0,1,2,…,K/2-1，u=0,1,2,…,R-1。值得注意的是，DZT变换可以通过FFT模块进行实现，这样大大减少了运算复杂度。

当初始滤波器p[v]满足对称条件p[v]=p[α+(2γ+1)N-v]时，根据式(18)可以推导得出正交滤波器p0[v]的Zak域表达式：

(20)

这里α∈[0,K-1]，γ∈Z，常数α和γ使得脉冲的长度能够任意选择。

根据以上分析以及多载波映射模块的特点，我们选择TFL性能最佳的高斯脉冲作为初始原型滤波器，脉冲序列正交化的步骤如下：

第一步：根据3.1节的介绍，首先构建离散高斯脉冲序列g[v]，将其作为初始滤波器，滤波器长度为L=K/2×R=NR。

第二步：计算g[v]的DZT变换矩阵Zg[v,u]。

第三步：根据公式(20)计算正交滤波器g0[k]的DZT变换矩阵Zg0[v,u]

第四步：对Zg0[v,u]进行DZT逆变换，即能得到长度为Lg的正交数字滤波器g0[v]。

上述变换得到的正交数字滤波器波形和幅频响应如图4(a)、图4 (b)所示，图4(c)给出了其正交映射的重构脉冲与原离散高斯脉冲对比效果。

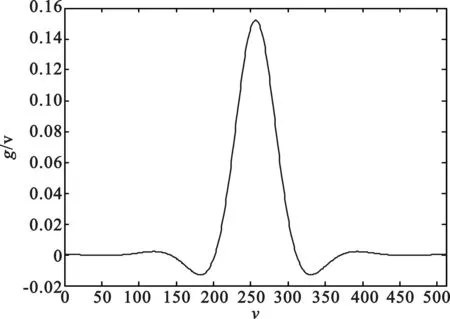
(a)数字正交滤波器波形

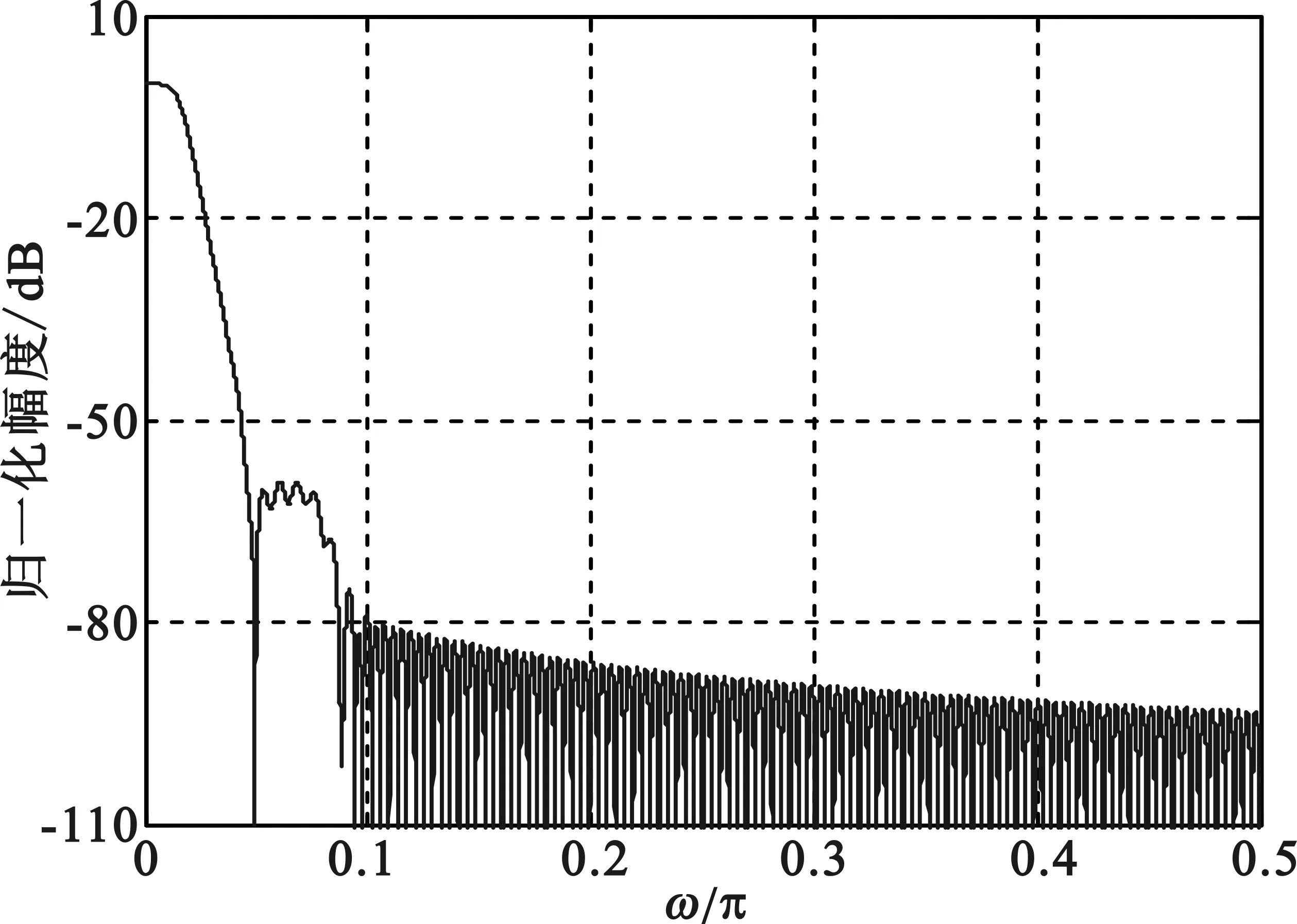
(b)幅频响应

(c) 正交基函数的映射重构信号

4仿真与数据分析

本节我们将对几种滤波器的映射性能进行系统仿真和数据分析。在仿真模型方面，设计系统子载波数K=128，时频间隔分别为T=F=1，时频压缩系数分别是TΔ=0.75，FΔ=0.9，正交基函数集元素个数Nt×Nf等于3×3。下面分别从映射精度、模块复杂度以及系统误比特率等方面进行分析和比较。

图5给出了几种正交滤波器的映射误差能量的分布情况，可以看出随着正交基数目的变化，基于高斯脉冲的离散正交滤波器始终具有最佳的映射精度。当正交基数目在8个以下时，四种滤波器的映射精度都比较差，随着基函数的增多，误差能量出现陡降，除了RRC滤波器之外，其他三种脉冲均可降至0.05以下，说明此时映射模块已经能够较好地重构信号。

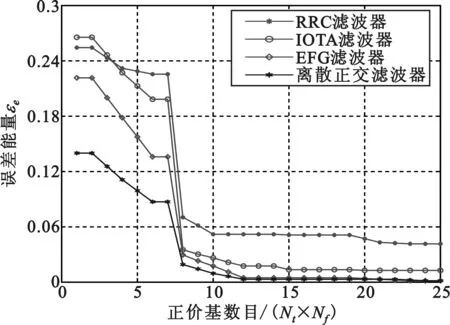
图5　不同正交滤波器的映射精度性能对比

复杂度是衡量映射模块性能的另一个重要指标，在2.3部分，我们针对三种原型滤波器，就单个FTN符号的映射计算复杂度进行了对比。引入正交数字滤波器之后，为方便比较，我们对整个映射模块的复杂度性能进行分析，结果如表2所示。可以看出EGF和IOTA滤波器的复杂度计算量最高。在仿真过程中，原型脉冲采样点数N相比子载波K一般需要高出若干数量级，达到103～104。因此很容易看出，即使相较于复杂度较低的RRC脉冲，数字正交滤波器也有着不错的优势。

表2　典型脉冲映射模块复杂度对比

文献[13]针对多载波FTN映射模块，提出了一种基于连续干扰消除(SIC)的接收方案，并结合了卷积编码和基于BCJR的迭代译码结构。利用该原理，我们建立了整个多载波FTN系统的收发机模型，并对不同成形滤波器下的系统的误比特性能进行了分析，如图6所示，可以看出，在整个信噪比范围内，离散正交滤波器性能最优。这是因为其在映射精度上的优势，更好地减轻了系统ISI和ICI。

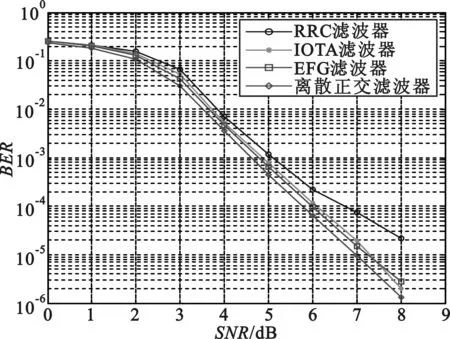
图6　采用不同滤波器的多载波FTN系统

5结语

映射模块的引入使得传统IFFT模块得以应用与多载波FTN系统，但同时也对脉冲成形滤波器提出了更高的要求。本文研究了基于OFDM/OQAM系统的多载波FTN脉冲分析与设计。定义了误差能量的概念，可以精确衡量映射精度。以此为基础，从多个角度对几种典型的原型滤波器映射性能进行了对比，分析表明EGF滤波器拥有相对较优的映射精度，但计算的复杂度较高。针对该问题，文章进一步提出了基于高斯脉冲的正交数字滤波器，将模块复杂度降低了一至两个数量级，并且提高了映射精度，从而取得了更优的系统误码性能。

参考文献：

[1]MazoJE.Faster-Than-NyquistSignaling[J].BellSystemTechnicalJournal, 1975, 54(8):1451-1462.

[2]AndersonJB,RusekF,OwallV,Faster-Than-NyquistSignaling[J].ProceedingsoftheIEEE, 2013, 101(8): 1817-1830.

[3]张雷，许飞，隋天宇. 4G移动通信技术在战术通信中的应用研究[J]. 通信技术，2015, 48(04):423-429.

ZhANGLei,XUFei,SUITian-yu.Applicationof4GMobileCommunicationTechnologyinTacticalCommunicationSystem[J].CommunicationsTechnology，2015, 48(04):423-429.

[4]RusekF,AndersonJB.TwoDimensionalMazoLimit[C]//.ProceedingsofIEEEInternationalSymposiumonInformationTheory,Adelaide:IEEEPress2005:970-974.

[5]RusekF,AndersonJB.MultistreamFasterthanNyquistSignaling[J].IEEETransactionsonCommunications, 2009, 57(5):1329-1340.

[6]DasalukunteD,RusekF,AndersonJB,etal.TransmitterArchitectureforFaster-Than-NyquistSignalingSystems[C]// 2009IEEEInternationalSymposiumonCircuitsandSystems(ISCAS2009).Taipei:IEEEPress, 2009: 1028-1031.

[7]DasalukunteD,RusekF,OWallV.MulticarrierFaster-Than-NyquistTransceivers:HardwareArchitectureandPerformanceAnalysis[J].Circuits&SystemsIRegularPapersIEEETransactionson, 2011, 58(4):827-838.

[8]RocheC,SiohanP.AFamilyofExtendedGaussianFunctionswithaNearlyOptimalLocalizationProperty[M].NewYork:SpringerUS,1997.

[9]VahlinA,HolteN.OptimalFiniteDurationPulsesforOFDM[J].IEEETransactionsonCommunications, 1996, 44(1):10-14.

[10]CHevillatP,UngerboeckG.OptimumFIRTransmitterandReceiverFiltersforDataTransmissionOverBand-LimitedChannels[J].IEEETransactionsonCommunications, 1982, 30(8):1909-1915.

[11]SiohanP,SicletC,LacailleN.AnalysisandDesignofOFDM/OQAMSystemsbasedonFilterBankTheory.[J].SignalProcessingIEEETransactionson, 2002, 50(5):1170-1183.

[12]BölcskeiH,DuhamelP,HleissR.OrthogonalizationofOFDM/OQAMPulseShapingFiltersusingtheDiscreteZakTransform[J].SignalProcessing, 2003, 83(7): 1379-1391.

[13]DasalukunteD,RusekF,AndersonJB,etal.DesignandImplementationofIterativeDecoderforFaster-than-NyquistSignalingMulticarrierSystems[C]// 2011IEEEComputerSocietyAnnualSymposiumon.VLSI(ISVLSI2011) ,Chennai:IEEEPress, 2011: 359-360.

Analysis and Design of Pulse Shaping Filters for Multicarrier FTN System

DUAN Hao1，GAO Yuan-yuan2，GUO Ming-xi2，ZHOU Zhi-yong1，NIE Sheng-yu1，XU Yang1

(1.Postgraduate Team 3,College of Communication Engineering;2.College of Communication Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

Abstract：The multicarrier FTN (faster-than-Nyquist) system would simultaneously introduced with inter-symbol interference and inter-carrier interference, thus raising the difficulty in realizing IFFT module. The concept of FTN mapper could fairly solve this problem, and however, the mapper would also pose further requirement for design of shaping filters. Based on OFDM/OQAM system, the mapping performance of various original filters is analyzed, and an evaluation parameter called error energy also deduced and defined, thus to effectively evaluated the mapping precision. An optimized digital filter from Gaussian pulse and based on the discrete-time formulation of multicarrier FTN signal is further designed. This filter could satisfy the discrete orthogonality condition strictly, and with less error energy and higher mapping precision, fairly improve the BER performance. In addition, the system complexity is reduced, being conducive to the hardware implementation of multicarrier FTN system.

Key words：multi-carrier FTN; pulse shaping filter; mapper; error energy; complexity

doi:10.3969/j.issn.1002-0802.2016.05.012

* 收稿日期：2015-12-16；修回日期：2016-03-26Received date:2015-12-16；Revised date：2016-03-26

基金项目：国家自然科学基金(No.61301157)

Foundation Item:National Natural Science Foundation of China(No.61301157)

中图分类号：TN911.7

文献标志码：A

文章编号：1002-0802(2016)05-0569-07

作者简介：

段昊(1991—)，男，硕士研究生，主要研究方向为高速无线通信技术；

高媛媛(1968—)女，博士，教授，主要研究方向为高速无线通信技术；

郭明喜(1978—)，男，博士，讲师，主要研究方向为高速无线通信技术；

周智勇(1990—)，男，硕士研究生，主要研究方向为网络信息系统工程；

聂晟昱(1990—)，男，硕士研究生，主要研究方向为高速无线通信技术；

徐洋(1990—)，男，硕士研究生，主要研究方向为高速无线通信技术。