基于预测的混和自动重传请求算法* 1

张　强，闫　斌，杨　蔚，周　辉

(1.电子科技大学 自动化工程学院，四川 成都 611731；2.四川省电力公司，四川 成都 610000)



基于预测的混和自动重传请求算法* 1

张强1，闫斌1，杨蔚2，周辉2

(1.电子科技大学 自动化工程学院，四川 成都 611731；2.四川省电力公司，四川 成都 610000)

摘要：为了解决无线传输过程中无线信道易受多径效应、抖动效应、衰落等因素的影响而使传输的有效性和可靠性得不到保障的问题，提出了一种基于预测的混和自动重传请求算法。利用隐马尔科夫模型预测传输过程中下一时刻的丢包率，根据不同时刻丢包率状态的比值关系动态调节里德-索洛蒙(Reed-Solomon)码的监督元数量。仿真结果表明,该算法与传统Ⅰ型混和自动重传请求(HARQ)算法和Ⅱ型混和自动重传请求(HARQ)算法相比，能够明显减少重传次数，降低误码率，通信可靠性明显提高。

关键词：无线传输；混和自动重传请求算法；隐马尔科夫模型；预测

0引言

无线通信环境中，无线信道常常受到噪声、多径效应、信号衰减等因素的影响，使得传输误码率较高，从而影响数据传输质量。因此，无线传输系统中采用差错控制技术具有重要意义。

差错控制的方式分为三类：前向纠错(FEC,ForwardErrorCorrection)、检错重传(ARQ,AutomaticRepeatreQuest)、 混合自动重传请求(HARQ,HybridAutomaticRepeatRequest)。前向纠错(FEC)方式是发送端编码器通过加入冗余信息的方式将所发信息编码成纠错码[1]，在接收端，若译码器有能力纠正接收到错误信息，则译码器自动对接收到的信息进行纠正。前向纠错无需将译码结果反馈给发送端，传输延迟小，但由于接收端无法完全纠正错误时不能反馈，所以其传输可靠性得不到保障，且由于纠错码冗余量恒定，无法适应时刻变化的信道。检错重传(ARQ)是发送端编码器将信息编码成可检错的码，根据接收的信息是否有错误向发送端发送反馈信号。若反馈否定信号，则将该信息重新发送；反之，则发送下一组信息。检错重传方式发送的检错码只需少许多余码元就可以使信息可靠传输，并且能够适应变化的信道，但由于反馈信道的存在，其传输延迟有所增大。Wozencraft在文献[2]中将FEC和ARQ相结合，阐述了HARQ的基本原理，首次提出HARQ算法，此算法被称为Ⅰ型HARQ。之后，Lin和Yu在1982年在文献[3]中提出了对Ⅰ型HARQ算法的改进，采用增量冗余的方式传输，被称为Ⅱ型HARQ。HARQ是FEC和ARQ的结合，信息块经过无线信道到达接收端后，如果信息块的错误数量在纠错码纠错范围内，则接收端译码器对其进行纠错；如果纠错码的纠错能力不足以纠正信息块中的错误，则通过反馈信号请求发送端重传此信息块。HARQ结合了ARQ和FEC的优点，在一定程度上减少了时延，提高了带宽利用率。但由于无线信道不稳定，随时都有可能变化，产生突发错误。

Gilbert在文献[4]中首次提出利用两状态的隐马尔科夫模型(HMM，hiddenMarkovmodel)对无线信道进行建模。目前，常用两状态的HMM即Gilbert模型作为无线传输包错误的模型[5]。但Gilbert模型不能精确的表示变化剧烈的信道特性。文献[6]利用三状态的HMM预测短波信道可用性，并根据预测结果选择接入信道，增大了信道利用时长，同时减少了切换率。Duarte在文献[7]中，利用HMM提出了一种自适应FEC算法，可以根据HMM的预测结果选择不同的FEC方案。文献[8]对HARQ系统中的自适应编码调制技术进行了研究，提出了HARQ和AMC相结合的跨层自适应传输方案。Fernando在文献[9]中提出利用Gilbert模型预测丢包率，并根据丢包率动态调节FEC参数。实验结果表明，预测模块对传输质量的提升起着重要作用。文献[10]在LDPC码的基础上提出了针对DSRC系统中IEEE802.11p协议的AMC和HARQ相结合的跨层设计，提高了频谱效率和吞吐量。文献[11]研究了基于分组码(STBC)的MIMO-HARQ系统，文章指出存在两类可快速解码的MIMO-HARQ系统：独立类型和依赖STBC结构类型。对于独立类型，提出了固定的和基于阈值的自适应方法。对于依赖STBC结构类，提出了针对HARQ算法的低计算复杂度的快速解码算法。

为了进一步增加无线传输过程中的效率及其可靠性，提出了一种基于预测的HARQ算法，利用HMM预测传输过程中下一时刻的丢包率，根据不同时刻丢包率状态的比值关系动态调节RS码的监督元数量。当下一时刻丢包率所对应的观测符号增大，则RS码监督元数随之增大，反之RS码监督元数量减小或不变。如果调整后的RS码依然不能使译码器纠正所有错误，则进一步增大监督元数量重新传输。

1无线信道丢包率预测模型

1.1隐Markov模型(HMM)

隐Markov模型(HMM)为Markov模型的扩展。HMM的状态是隐藏的，每个隐藏状态会按照一定概率产生观测符号。所以，隐含状态可以通过观测符号来反映。

一个HMM可由以下五个元素来表示：

1)隐含状态S。隐含状态是不可见的，某些情况下无实际的物理意义，但在大多数实际应用中，是有确切的物理意义的。隐含状态集合可以表示为S={S1,S2,…,SN},t时刻的状态表示为qt。

2)隐含状态所对应的观测序列O。观测序列集合可表示为O={O1,O2,…,OM}。

3)状态转移矩阵A={aij}N×N。其中，aij=p{qt+1=Sj|qt=Si},1≤i,j≤N,即从状态i转换到状态j的概率。

4)观测符号概率分布矩阵B={bjk}N×M。其中，bjk={Ok|qt=Sj}，1≤j≤N，1≤k≤M。表示状态为Sj时产生观测状态为k的概率。

5)初始状态分布π={πi}。其中，πi=p{q1=Si}，1≤i≤N。

一个HMM模型可由集合λ={A,B,π}确定。

1.2隐Markov模型对丢包率的预测

采用六状态的HMM，根据信噪比SNR划分，隐含状态与SNR的对应关系如表1所示。

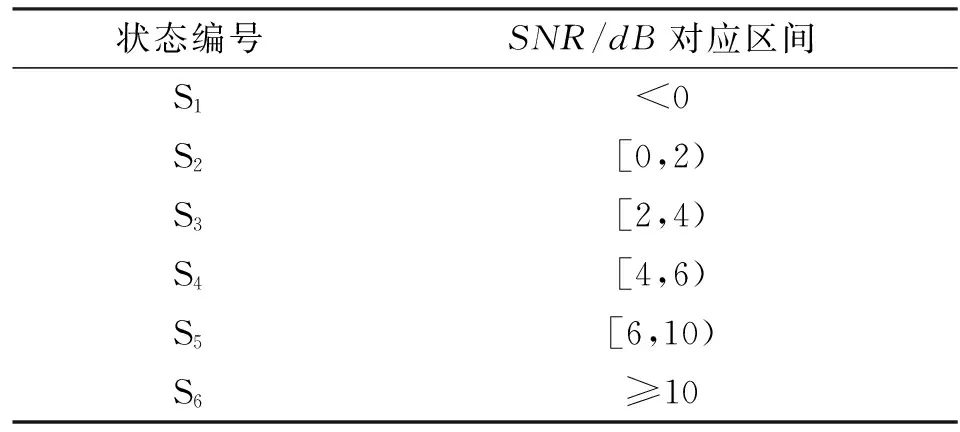
表1　隐含状态与SNR对应关系

观测序列O={O1,O2,…,O15,O16}根据每秒的丢包率划分，划分标准：[0%,1%)为O1,[1%,2%)为O2，…，[14%,15%)为O15，[15%,100%]为O16。

状态转移矩阵A和观测符号概率分布矩阵B可由Baum-Welch算法得到。首先通过初始化样本得到初始时刻隐含状态概率分布π={p{q1=Si}},1≤i≤6。

定义前向变量:

αt(i)=p(O1O2…Ot,qt=Si|λ)

(1)

为给定模型λ及t时刻状态Si，从开始到t时刻观测序列为O1,O2,…,Ot的概率。

定义后向变量:

βt(i)=p{Ot+1Ot+2…OT|qt=Si,λ}

(2)

为给定模型λ及t时刻状态Si，从t+1时刻到最后时刻观测序列为Ot+1,Ot+2,…,OT的概率。

给定观测序列和模型λ，t时刻状态为Si，t+1时刻状态为Sj的概率为：

ξt(i,j)=p{qt=Si,qt+1=Sj|O,λ}

(3)

由前向变量和后向变量可得：

(4)

于是，

(5)

在时间上对rt(i)求和，得到由状态Si转换的数学期望。类似的，在时间上对ξt(i,j)求和，可得从状态Si转换到状态Sj的数学期望。于是，得到λ={A,B,π}的重新估计值：

(6)

(7)

(8)

根据以上步骤，反复的进行重新估计，直到观测值的概率达到阈值,则得到HMM模型的最佳参数。通过Viterbi算法，可以得到一个与给定观测序列O={O1,O2,…,OT}的最佳匹配状态序列Q={q1,q2,…,qT}。则下一时刻隐含状态为：

qT+1=argmax(aqTj),1≤j≤6

(9)

于是，下一时刻所对应的观测符号为：

OT+1=argmax(bqT+1k),1≤k≤16

(10)

2基于预测的混和自动重传请求算法

丢包率为信道状态的一种反应，丢包率的变化意味着信道状态的变化，同时误码率也会随信道状态的变化而变化。所以，误码率与丢包率存在正相关关系。基于预测的HARQ算法利用隐马尔科夫模型预测传输过程中下一时刻的丢包率，根据不同时刻丢包率所对应观测符号的比值动态调节监督元数量。RS码编译码简单，且给定码长n和纠错能力m时，能直接确定一个RS码，适合预先设定码的纠错能力。对于RS码，2m个监督元，可以纠正m个错误。

第t秒与第t+1秒观测符号比值为：

(11)

式中，t秒时RS码监督元数量为ut，则t+1秒时RS码监督元数量为：

ut+1=Int(ut×dt,t+1)+1

(12)

式中，Int()表示向下取整运算。设定最大及最小监督元数目，如果ut+1超过最大监督元数目，则以最大监督元数目作为编码方案，如果ut+1小于最小监督元数目则以最小监督元数目作为编码方案。

同时，设定最大传输次数，若接收端译码失败，则由反馈信道传输否定信号，编码器下一次传输则增加一定量的监督元数目。此时，如果监督元数量超过上限，则采用最大监督元数目方案。

基于预测的HARQ算法具体步骤如下：

1)根据初始样本初始化HMM参数A、B、π。

2)通过Viterbi算法根据已知的观测序列计算出隐含状态序列。

3)根据式(9)得到下一个隐含状态。

4)根据式(10)得到下一状态所对应的观测符号。

5)通过式(11)和式(12)得到下一秒RS编码所需的监督元数量，确定编码方案。如果监督元数量达到上限，则以最大冗余量作为编码方案；如果监督元数量低于下限，则以最小冗余量作为编码方案。

6)判断译码是否成功，如果不成功且传输次数小于最大传输次数，则增加冗余量后再次传输。如果冗余量高于上限或低于下限，则以最大监督元数或最小监督元数为编码方案。

7)经过一段时间τ，利用Baum-Welch算法重新估计HMM参数A、B、π。

此算法计算代价主要集中在利用Baum-Welch算法重新估计HMM参数。文献[12]对Baum-Welch算法复杂度进行了详细叙述，利用Baum-Welch算法进行参数估计的每次迭代运算复杂度为O(N2T)，其中，N为HMM隐含状态数量，T为样本数量。其计算复杂度会随着隐含状态数量的增多而迅速增大。

3实验结果与分析

利用MATLAB仿真工具对该算法进行仿真，并与Ⅰ型HARQ算法和Ⅱ型HARQ算法进行比较。以前20s观测序列作为初始样本对HMM模型进行训练得到其参数λ={A,B,π}。RS码码长设置为n=26-1=63，由63个码字组成，每个码字含6比特数据，每个码组有378比特。设定RS码冗余度最高为(63，11)编码方案，最低为(63，51)编码方案。最大传输次数为5，当接收端译码失败，则由反馈信道传输否定信号，编码器下一次传输则增加10个监督码元，如果监督码元数量超过51则保持(63,11)码不变。每隔1s统计一次丢包率并计算出相对应的观测符号，每隔3min利用Baum-Welch算法重新估计HMM参数。

对于Ⅰ型HARQ算法，RS码始终采用(63,31)编码方案，即每个码组中存在32个监督元，可以纠正16个错误码字。最大传输次数为5次且每次重传监督元数量不变。对于Ⅱ型HARQ算法，RS编码采用增量冗余的传输方案。每次重传监督元都进一步增多，直到成功译码或传输次数超过5次。

采用改进HARQ算法与Ⅰ型HARQ算法、Ⅱ型HARQ算法进行传输的误码率仿真对比图如图1所示。从图中可以看出改进的HARQ算法能够使误码率急剧下降，在4dB时能使误码率降为0；Ⅱ型HARQ算法可以变更RS码的码率，其误码率降低速度优于Ⅰ型HARQ算法，但相对于改进的HARQ算法较差；Ⅰ型HARQ算法，不可变更RS码码率，在降低误码率方面效果最差。

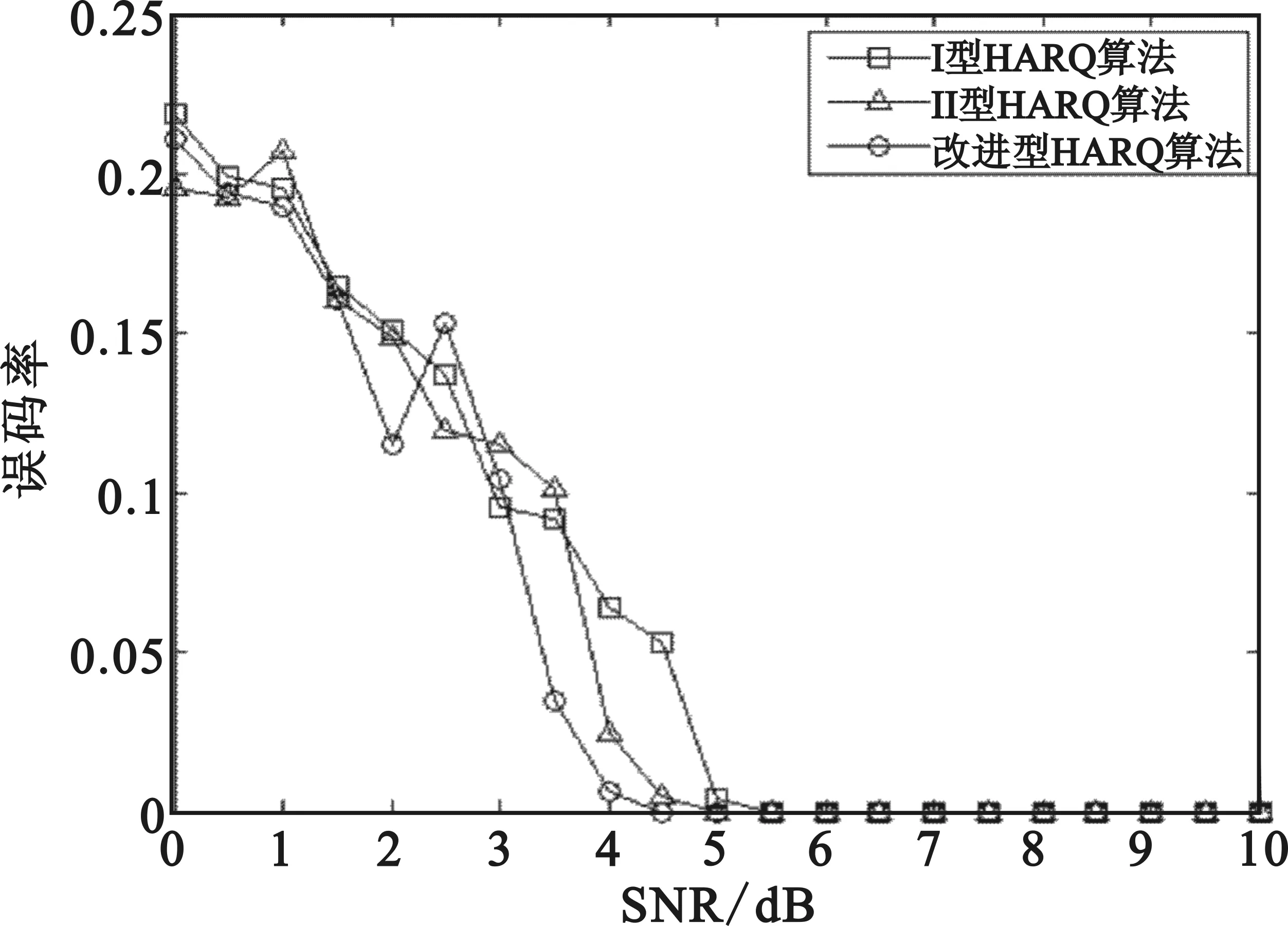
图1　改进HARQ算法与Ⅰ型HARQ算法、

三种算法传输过程中对于传输次数的仿真如图2所示。在信噪比较低时，误码较多，采用冗余度最高编码方案也无法完全纠正错误，所以SNR在3dB之前传输次数为最大传输次数。在此之后，改进的HARQ算法由于可以通过预测在传输之前确定合适的RS码率策略，所以传输次数迅速降为1次。Ⅰ型HARQ算法始终采用(63,31)编码方案，而Ⅱ型HARQ算法第一次传输采用较少监督元的方案，随着重传次数的增加接收端码率逐渐降低。所以，Ⅰ型HARQ算法传输次数略少于Ⅱ型HARQ算法。

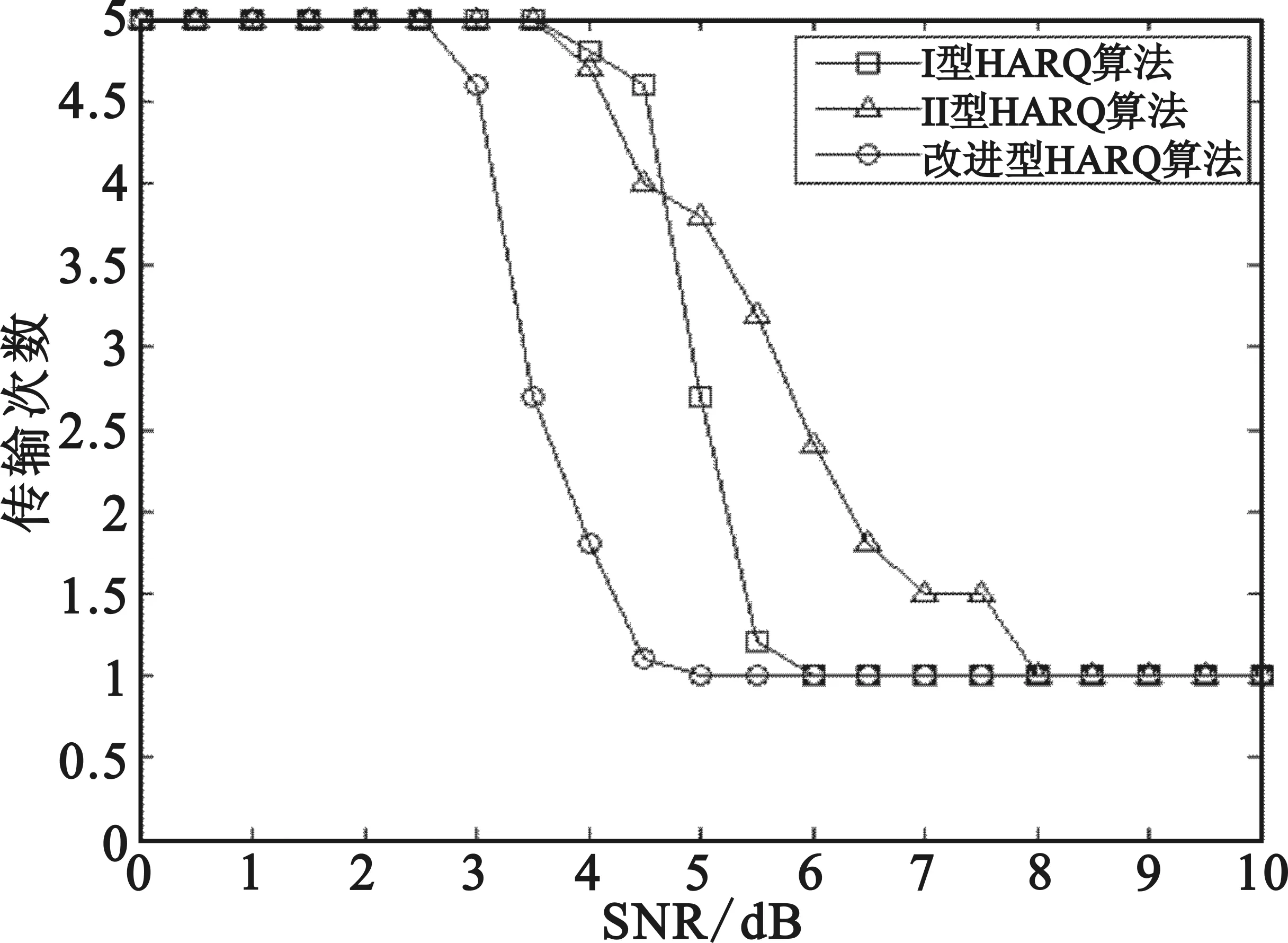
图2　改进HARQ算法与Ⅰ型HARQ算法、

定义吞吐量为正确接收的信息比特数除以为了正确传输这些信息而发送的所有比特数[13]。改进的HARQ算法与Ⅰ型HARQ算法、Ⅱ型HARQ算法传输过程中吞吐量仿真对比图如图3所示。从图3可以看出，改进的HARQ算法可以使吞吐量迅速上升，而采用Ⅰ型HARQ算法和Ⅱ型HARQ算法时，吞吐量上升较为缓慢。然而，对于改进的HARQ算法来说，信道状况较好时的观测符号1所对应的丢包率为[0%,1%),所以在观测符号为1时，所采用的RS编码方案为可以解决状态1最坏情况的编码方案，即丢包率为1%时的方案。所以，在信噪比很高的情况下，改进的HARQ算法吞吐量略低于第一次传输监督元较少的Ⅱ型HARQ算法。Ⅰ型HARQ算法始终采用编码方案(63,31)，所以其吞吐量最大为31/63。

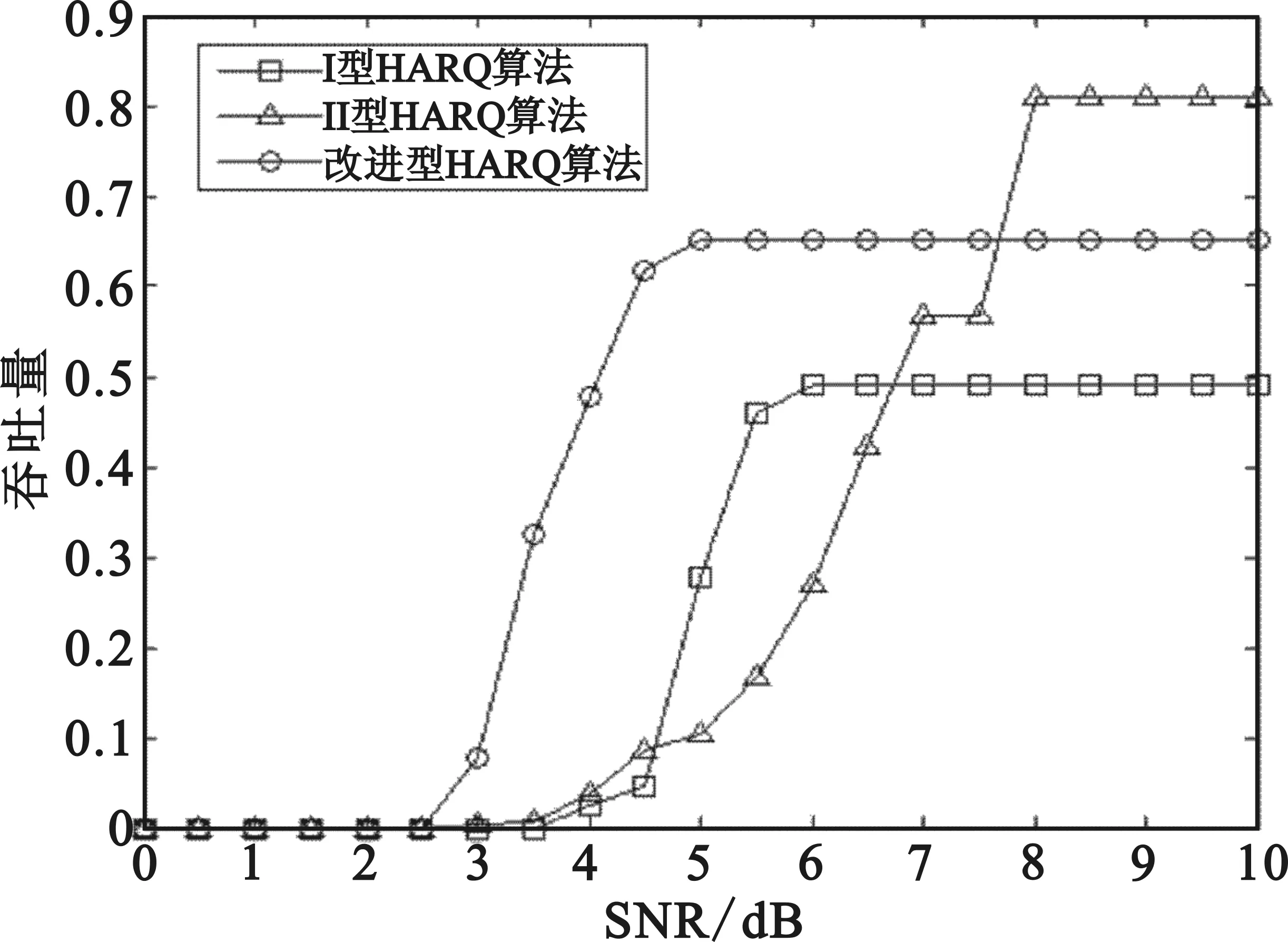
图3　改进HARQ算法与Ⅰ型HARQ算法、

改进的HARQ算法与Ⅰ型HARQ算法、Ⅱ型HARQ算法传输过程中单位时间内有效比特数仿真对比图如图4所示。

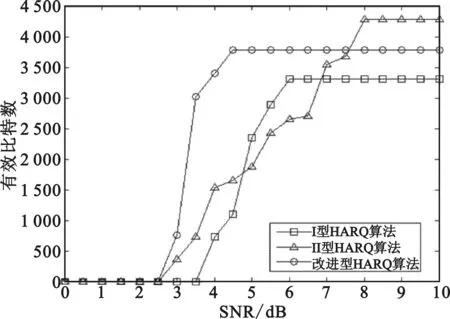
图4　改进HARQ算法与Ⅰ型HARQ算法、

从图4中可以看出，改进的HARQ算法有效比特数上升较快，而传统HARQ算法有效比特数上升缓慢。由于改进的HARQ算法吞吐量小于Ⅱ型HARQ算法，所以在信噪比较高传输次数为1时，其有效比特数略小于Ⅱ型HARQ算法。值得提出的是，代码编写方式以及仿真计算机硬件的不同会造成传输有效比特数的差异。

4结语

针对无线信道易受外界干扰而使传输质量得不到保障的问题，本文提出了一种基于HMM预测的HARQ算法。利用HMM预测传输过程中的丢包率，并通过丢包率状态的比值关系确定下一时刻所采用的RS编码方案。仿真实验表明，通过自适应调节RS编码冗余量，能够使接收信息拥有较低的误码率，信道SNR在4dB时误码率即可降为0，提高了无线传输系统的传输可靠性。并且，能够使传输次数迅速降为1次，随着重传次数的减少，传输效率随之增高。同时，吞吐量上升速度也迅速增高。对于该算法的进一步研究，可以从丢包率状态划分入手，更精细的丢包率状态划分可以得到更高的最大吞吐量。

参考文献：

[1]赵琦，刘荣科.编码理论[M].北京：北京航空航天大学出版社，2009.

ZHAOQi,LIURong-ke.CodingTheory[M].Beijing:BeihangUniversityPress,2009.

[2]Wozencraft,JohnM,Horstein,Michael.CodingforTwo-WayChannels[D].MassachusettsInstituteofTechnology,ResearchLaboratoryofElectronics.1961.

[3]LINS,YUPS.AHybridARQSchemewithParityRetransmissionforErrorControlofSatelliteChannels[J].Communications,IEEETransactionsoncommunications,1982,30(7):1701-1719.

[4]GilbertEN.CapacityofaBurst-NoiseChannel.BellSystemTechnicalJournal[J].1960,Vol.39(5):1253-1265.

[5]张珍明.无线视频传输关键技术研究[D].武汉：华中科技大学，2006.

ZHANGZhen-ming.KeyTechnologyofVideoTransmissionoverWirelessChannel[D].Wuhan:HuazhongUniversityofScienceandTechnology,2006.

[6]林刚，程云鹏，江汉.一种基于HMM预测的短波信道接入方法[J].通信技术，48(12):1377-1383.

LINGang,CHENGYun-peng,HANJiang.AShortwaveChannelAccessMethodbasedonHMMPrediction[J].CommunicationsTechnology,48(12):1377-1383

[7]DuarteFP,EAdeSouzaeSilva,DonTowsley.AnAdaptiveFECAlgorithmusingHiddenMarkovChains[J].ACMSIGMETRICSPerformanceEvaluationReview.2003.vol.31(2):11-13

[8]李长春.自适应传输关键技术与研究应用[D].济南：山东大学，2011.

LIChang-chun.ResearchonKeyTechnologiesandApplicationsofAdapativeTransmission.Jinan:ShandongUniversity,2011.

[9]FernandoS,Edmundo.PredictingPacketLossStatisticswithHiddenMarkovModelsforFECControl[J].ComputerNetworks.2012,vol.56(2):628-641.

[10]ZHANGGao-yuan,SUNLi-min,WENHong,WUBin,ZHUXi-ping,ZHOULiang-huang,LIUSheng.ACross-LayerDesignCombiningofAMCwithHARQforDSRCSystems[J].InternationalJournalofDistributedSensorNetworks,2013,Vol.15(4):2122-2122.

[11]HosseiniSS,AboueiJ,UysalM.Fast-DecodableMIMOHARQSystems[J].IEEETransactionsonWirelessCommunications,2015,Vol.14(5):2827-2840.

[12]RabinerLR.ATutorialonHiddenMarkovModelsandSelectedApplicationsinSpeechRecognition[J].ProceedingsoftheIEEE,1989,Vol.77(2):257-286.

[13]姜维.混合自动请求重传技术的性能研究[D].济南：山东大学，2008.

WEIJiang.HARQTechnologythePerformanceStudy[D].Jinan:ShandongUniversity,2008.

AHybridAutomaticRepeatRequestAlgorithmbasedonPrediction

ZHANGQiang1,YANBin1,YANGWei2,ZHOUHui2

(1.SchoolofAutomationEngineering,UniversityofElectronicScienceandTechnologyofChina,ChengduSichuan611731,China;2.SichuanElectricPowerCompany,ChengduSichuan610000,China)

Abstract：In order to solve the problem of transmission validity and reliability with the influence factors including multipath effect,jitter effect and fading,a hybrid automatic repeat request algorithm based on prediction is proposed.By using the hidden Markov model to predict the packet-loss rate of the next time during the transfer process,and in accordance with the ratio of packet-loss rate at different times,the redundancy in Reed-Solomon codes is tuned.Simulation results indicate that compared with the traditional type-Ⅰhybrid automatic repeat request algorithm and the type-Ⅱhybrid automatic repeat request algorithm,the proposed algorithm could significantly reduce the number of retransmission times,and the bit error rate,and remarkably raise the communication reliability.Key words：wireless transmission;hybrid automatic repeat request algorithm;hidden Markov model;predicting

doi:10.3969/j.issn.1002-0802.2016.05.007

* 收稿日期：2015-12-20；修回日期：2016-04-05Received date:2015-12-20；Revised date：2016-04-05

中图分类号：TP301.6

文献标志码：A

文章编号：1002-0802(2016)05-0544-05

作者简介：

张强(1990—)，男，硕士研究生，主要研究方向为无线传输；

闫斌(1974—)，男，博士，讲师，主要研究方向为无线传感器网络；

杨蔚(1978—)，男，学士，工程师，主要研究方向为物联网技术与智能电网应用；

周辉(1985—)，男，学士，助理工程师，主要研究方向为物联网技术与智能电网应用。