数形结合思想在概率论教学中的应用
李璇 王斌 鲁砚青 兰莉莉

【摘要】概率论是一门研究事情发生可能性的学科,在生活生产中应用广泛,但也是学生较难掌握的一门课程,如果在教学中运用数形结合的思想则能使很多复杂的概率问题得以直观化清晰化,从而达到提高学生学习效率的目的.
一、引 言
概率论作为一门研究随机性或者不确定现象的学科,有其广泛的应用性,为此很多高等院校的工科类及经管类专业都将其作为专业基础课程,但是,由于我们所研究的概率问题的抽象性使得这门课程成为很多学生学习的障碍,另外由于这门学科的很多内容都与高等数学的知识有很大的关联性,因此对于那些数学基础相对薄弱的学生而言,概率论是他们的弱项学科.数形结合思想是数学中常用的思想之一,它贯穿于学生的小学中学的数学学习中,使用这种方法可以起到“以行助教”的作用,可以使一些复杂抽象的数学问题变得直观化、生动化,从而使难题迎刃而解,达到事半功倍的效果.
二、数形结合方法计算几何概型的概率
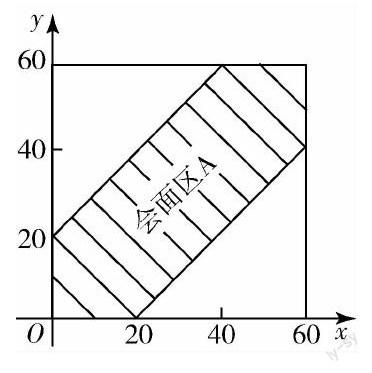
例1 甲、乙两人相约在7点到8点之间在某地会面,先到者等候另一人20分钟,过时就离开,如果没人可在指定的一小时内任意时刻到达,试计算两人能够会面的概率.
分析 根据题意,很容易看到这种概率模型应属于几何概型,因此我们可以套用计算几何概型的公式,但是由于问题的抽象性很多学生并不清楚样本空间和两人能够会面所表示的区域大小,通过结合图形讲授此类题目,很多学生便能够轻而易举地解决.
解 记7点为计算时刻的0时,以分钟为单位,x,y分别记为甲、乙到达指定地点的时刻.
第一步:在二维平面上做x轴,y轴,分别表示甲、乙到达指定地点的时刻,则整个空间为S={(x,y)|0≤x≤60,0≤y≤60}.
第二步:以事件A表示“两人能会面”,依题意,只有两人到达的时刻差小于20时可以会面,因此A={(x,y)|(x,y)∈S,|x-y|≤20},在图像上作出相应的直线.
第三步:结合图像,我们可以看到阴影部分代表“两人能会面”,而正方形的面积代表整个样本空間,根据计算几何概型概率的公式即可得到P(A)=μ(A)μ(S)=602-402602=59.
三、数形结合方法求解一维连续型随机变量函数的概率密度函数
求解一维连续型随机变量函数的概率密度函数一直是概率论学习中的难点问题,一部分学生喜欢套用课本中提到的概率密度公式,却忽略了这种方法的使用条件(函数必须是严格单调的),另一部分学生则对于具体的计算题目不知如何处理,运用数形结合的方法则能很好地解决这些问题.
例2 设随机变量X概率密度为fX(x)=2xπ2,0四、数形结合方法求解二维连续型随机变量函数的概率密度函数
二维连续型随机变量函数的概率密度函数的求解方法类似于一维的情形,但是由于二维的计算上更加困难,学生通常用卷积公式来求解这类问题,实际上通过数形结合的方法可以使这类问题的求解一目了然,易懂易学.
五、总 结
以上几个例题可以看出数形结合方法在概率论教学中的重要性,通过这一方法可以将一些复杂的概率问题变得清晰化直观化,实践也证明,在教学过程中融入数形结合的思想,可以增强学生的学习兴趣,提高学生的学习效率.

