基于分区补给物质平衡法预测致密油压裂水平井动态储量

魏漪，冉启全，李冉，袁江如，董家辛（1.国家能源致密油气研发中心；2.中国石油勘探开发研究院）



基于分区补给物质平衡法预测致密油压裂水平井动态储量

魏漪1， 2，冉启全1， 2，李冉1， 2，袁江如1， 2，董家辛1， 2
（1.国家能源致密油气研发中心；2.中国石油勘探开发研究院）

摘要：为了克服常规物质平衡法的局限，针对致密油储集层非均质性强的特点，将致密油压裂水平井的渗流区域分为高渗区和低渗区，并将其等效为径向复合渗流模型。以平行板理论为基础，将各区的多重介质等效为一种连续性介质，基于致密油多重介质的非线性渗流机理，结合积分法，提出采用两区补给物质平衡法计算致密油压裂水平井动态储量，并分区建立相应的压力分布方程和物质平衡方程。该方法结合实际生产动态规律，考虑了两类渗流区交界面处压力突变和流体交换，更符合生产实际情况。实例计算表明，应用该方法可以确定出单井控制范围内的动态储量以及不同开采时间低渗区对高渗区的补给量，为生产井产量及工作制度的确定、开发井网的部署和调整提供依据。图9参22

关键词：致密油；压裂水平井；压力分布；动态储量；分区补给；物质平衡法

0 引言

动态储量是指油气藏连通孔隙体积内，在现有开采技术水平条件和现阶段下最终能够有效流动的流体折算到标准条件的总体积量［1］。对于已经投入开发的油气藏，动态储量是评价开发状况的关键指标之一。目前，计算动态储量的方法［1-7］主要有不稳定试井法、产量递减法、产量累计法和物质平衡法，其中物质平衡法是较为有效和准确的方法。常规物质平衡法［8］假设岩石和流体性质在空间上没有变化，流体在多孔介质中的流动瞬间达到平衡，油气藏均匀动用，根据油气体积的地下平衡计算不同地层压力下的产出量。该方法适用于渗透性、连通性较好的油气藏。但对非均质性很强的复杂低渗油藏，该方法计算的储量往往难以准确反映油藏或者单井控制的动态储量［8-9］。针对此类油气藏，近年很多学者对常规物质平衡方法进行了改进［2-7］，提出分区物质平衡法的概念和思路，但研究对象多以气藏为主。

目前国内外主要采用“水平井钻井+水平井分段压裂”的开发模式实现致密油资源的有效动用。在此模式下，致密油储集层中形成不同尺度裂缝，多尺度裂缝与基质耦合，因此，其渗流机理复杂，在单口压裂水平井控制范围内，储集层的非均质性很强，常规物质平衡法无法准确预测出其动态储量。现有的分区物质平衡法也未对致密油储集层多重介质耦合下的压裂水平井动态储量进行较为准确的预测。

本文基于致密油多重介质的非线性渗流机理，考虑启动压力梯度、应力敏感效应等因素的影响，提出了两区补给物质平衡法计算致密油压裂水平井动态储量的新方法。以单井为研究对象，其渗流区域可分为高渗区和低渗区，将各区的多重介质等效为一种连续性介质，分区建立相应的非线性渗流模型，考虑两类渗流区交界面处的压力突变和流体交换，结合积分法求取各区的压力分布方程，根据地层压力判定油藏类型，对饱和与未饱和的两种油藏类型，建立各区相应的物质平衡方程，确定出各区的动态储量及不同开采时间内低渗区对高渗区的补给量，最终得到致密油压裂水平井单井动态储量。

1 压裂水平井动态储量模型

1.1 研究思路

对于致密油储集层，通常选择天然裂缝发育的甜点区进行布井，水平井分段压裂施工中天然裂缝开启，与人工水力裂缝形成复杂的裂缝网络，基质中流体以“最短距离”渗流的方式流向裂缝，再沿着裂缝网络流到井筒，提高了单井控制范围内储集层整体渗透率，极大地增加了储集层的有效动用率［10-12］。

MONGALVY等人以水力压裂措施所产生的复杂裂缝网络为基准，将单井泄油区域划分成两部分，即井筒附近包含裂缝网络的有效改造体积（ESRV）和有效改造体积周围未改造体积（UnSRV）［13］，其中，裂缝网络又可分为两套裂缝体系，即靠近井筒的具有高导流能力的裂缝网络和ESRV内的未支撑或支撑较差的裂缝网络。

在资料有限的条件下，一般很难准确得到ESRV边界。因此，本文在对单井泄油范围进行分区建立模型时，以水平井端面和人工水力裂缝尖端所形成的矩形区域为基准（见图1），矩形区内的1区主要由ESRV内靠近井筒的具有高导流能力的裂缝网络即支撑的裂缝网络和基质组成，其储集层渗透率较高，称为高渗1区；矩形区外的2区主要由ESRV内的未支撑或支撑较差的裂缝网络和相应的基质、UnSRV内的基质组成，其储集层渗透率较低，称为低渗2区。

单井整个控制范围内储集层非均质性强，两个渗流区分别发育不同的孔缝介质，其储集层参数各不相同，但在同一渗流区内其平均物性参数相同，而在两区交界面上物性参数呈跳跃式变化。单井泄油区理论上是矩形区域，难以建立相应的不稳定渗流模型，为了便于模型的建立和求解，在多重介质等效的基础上，将两个渗流区等效为径向复合渗流模型，单井泄油区也相应等效为径向渗流区（见图2），油井位于高渗1区的中心。

图1　压裂水平井泄流区域示意图

图2　单井等效径向渗流模型分区示意图

开发初期，首先动用的是高渗区的储量，随着生产的进行，压力波传播到高渗1区的边界（T0时刻），低渗2区中的流体开始流动，在压差的作用下，2区流体开始向1区进行补给，2区的储量开始动用。随着压力波的传播，2区动用的面积也在不断增加，但1区的面积保持不变。在实际典型生产动态曲线上，生产初期产量较高，高渗区流体快速产出，低渗区补给缓慢，产量快速下降；生产后期，低渗区不断补给，产量保持稳定，但流速较慢，产量较低。

开采过程中两个渗流区的地层压力有显著差别，分别针对高渗区和低渗区建立相应的渗流模型，求取各区的压力分布方程，再利用物质平衡法分别计算出高渗区和低渗区的动态储量，最终得到单井控制的总动态储量。

1.2 辅助模型

两个渗流区等效为径向复合渗流模型后，需计算等效径向渗流区大小及物性参数，另外，对于致密储集层，需考虑启动压力梯度、应力敏感效应等因素的影响。

1.2.1 渗流区范围等效

设定的高渗1区为一个矩形渗流区，长为水平段长度，宽为人工水力裂缝长度，因此高渗1区的面积固定不变，高渗1区的等效泄油半径R1也是一个定值。由面积等效原则，可得到R1的表达式：

低渗2区从水平段和水力裂缝的端面向外延伸的距离即为该区基质的泄油半径re（t），与该区域的渗透率、启动压力梯度、应力敏感效应、地层压力等因素有关，是一个随时间、压力变化的非稳态值。因此，与re（t）相关的低渗2区的等效泄油半径R2也是一个随时间、压力变化的非稳态值。由面积等效原则，可得到R2的表达式：

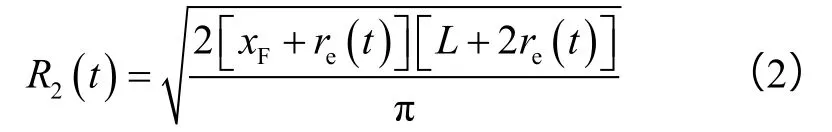
1.2.2 物性参数等效

以平行板理论为基础，利用渗流力学相关理论，建立致密油储集层的等效连续介质模型。假设各渗流区域的裂缝分布均匀，裂缝间相互平行，方向一致，且都为垂直裂缝，裂缝在平面上和纵向上完全贯通［14-18］。

高渗1区中的流动介质包括水力裂缝、天然微裂缝和基质，而低渗2区的流动介质为天然裂缝和基质。根据等值渗流阻力原理及水电相似原理得到高渗1区等效渗透率和孔隙度的表达式：

低渗2区的等效渗透率和孔隙度的表达式为：

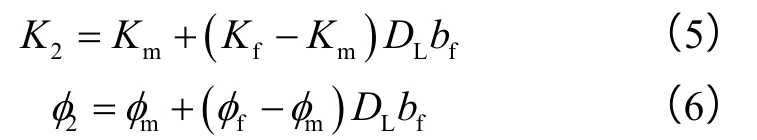
1.2.3 启动压力梯度

致密油储集层主要发育纳—微米级孔喉，表现为低速非达西渗流特征，流体渗流受启动压力梯度的影响显著，随着渗透率的降低，启动压力梯度不断增加。

通过大量的实验数据回归得到，储集层启动压力梯度与渗透率间呈幂指数关系：

分析非线性渗流实验数据发现，不同油田、不同储集层的启动压力梯度随渗透率的变化趋势相同，即都呈幂指数关系，但其各自关系式中的系数a、b值不同。在实际应用中，应根据实际储集层或者特性相近的储集层的实验数据进行回归，得到相应的关系式。

1.2.4 应力敏感性

随着地层压力的降低，基质孔隙、天然裂缝和水力裂缝均发生不同程度的变形。基质孔隙发生收缩变形；随着支撑剂破碎或失效，裂缝发生变形或者闭合。这些变形导致储集层物性发生变化，从而对流体渗流产生一定的影响。

通过大量实验数据的分析发现，戈尔布诺夫［19］提出的指数表达式对实验数据的回归相关系数最高，基质和裂缝变形引起的渗透率应力敏感关系式分别为：

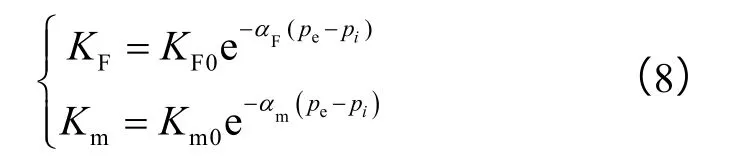
基质和裂缝均具有一定程度的应力敏感性，因此，高渗1区和低渗2区的等效渗透率也随着地层压力的变化而变化。将（8）式代入（3）式、（5）式中，即可得到各区等效渗透率随地层压力变化的关系式K1（p1）、K2（p2）。

1.3 两区压力计算模型

地层压力对动态储量的影响很大，在开采过程中，致密油压裂水平井个渗流区的地层压力有显著差别，分别针对高渗区和低渗区建立相应的非线性渗流模型，求取各区的压力分布方程。

1.3.1 压力波传播到高渗1区边界前

压力波传播到高渗1区边界前，t小于等于T0，压力波传播距离R（t）小于等于R1，此时，仅高渗1区的流体流动，低渗2区的流体不流动。其不稳定渗流方程为：

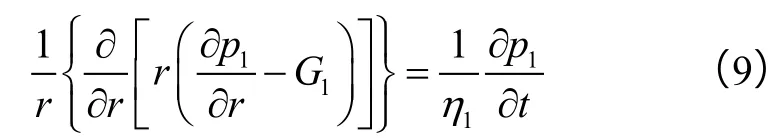
内边界条件：

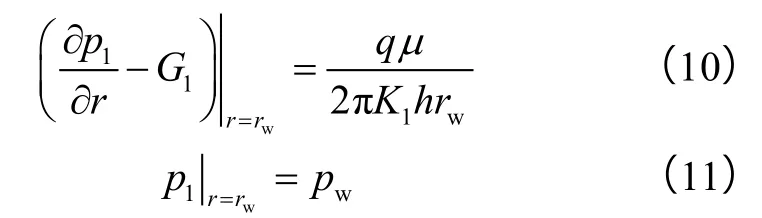
外边界条件：

为了简化不稳定渗流模型的求解过程，只能求取其近似解，假设激动区（即压力波所波及到的范围）压力分布可以由坐标的对数和指数多项式表示，采用积分法［20］求致密油平面径向不稳定渗流的近似解。考虑到计算的复杂性，根据精度要求（忽略高次项），高渗1区的压力分布表示为：

将（13）式代入（10）式—（12）式3个边界条件中，并进行求解，得到系数a0、a1、a2，即：

将a0、a1、a2代入（13）式中，可以得到地层压力方程p1（r，t）。

当r=R1时，p1（R1，T0）=pe，由（13）式可求得T0时刻的q值，根据实际生产数据或者模拟得到的产能规律，即可求得T0值。

在压力波传播到1区边界R1处前，即t小于等于T0的任意时刻，压力波传播的边界R（t）处的压力均为pe，即：由此结合实际生产数据或者模拟得到的产能规律，可以得到任意时刻t对应的产量q。将q（t）代入方程中，即可计算出t小于等于T0时间内，不同时刻的压力波传播距离R。

由地层压力方程p1（r，t），可以得到t小于等于T0时间段内任一时刻下泄油区的平均地层压力：

1.3.2 压力波传播到高渗1区边界后

压力波传播到高渗1区边界后，t大于T0，压力波传播距离R（t）大于R1，此时，低渗2区的流体开始流动，2区流体开始向1区进行补给，随着压力波的传播，2区动用的面积不断增加。

两区交界面处储集层特性和流体特性突变，存在流体交换［21-22］。开采过程中，高渗1区和低渗2区的地层压力分布有显著差别，分别建立相应的渗流模型，求取各区的压力分布方程。

①高渗1区

其不稳定渗流方程同（9）式，内边界条件同（10）式、（11）式。

其外边界条件，即交界面处的连续条件为：

高渗1区的压力分布由积分法表示为：

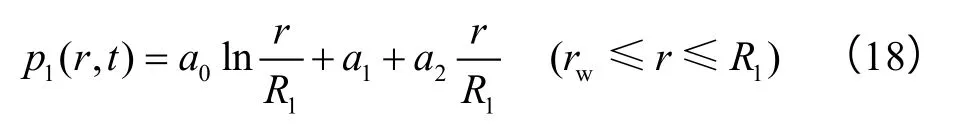
将（18）式代入（10）式、（16）式、（17）式3个边界条件中，并进行求解，得到系数a0、a1、a2，即

将a0、a1、a2代入（18）式中，可以得到高渗1区的地层压力分布方程p1（r，t）。

由地层压力方程p1（r，t），可以得到t大于T0时间段内任一时刻高渗1区的平均地层压力：

将p1（r，t）代入（11）式可以得到：

②低渗2区

其不稳定渗流方程为：

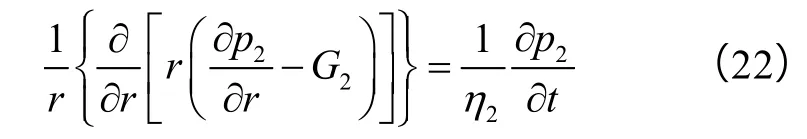
外边界条件：

内边界条件，即交界面处的连续条件：

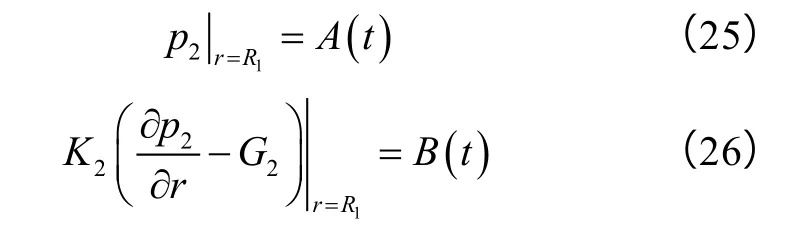
低渗2区的压力分布由积分法表示为：

将（27）式代入（23）式、（25）式、（26）式中，并进行求解，得到系数a0′、a1′、a2′，即：

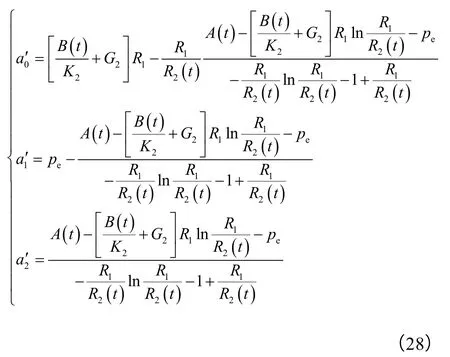
将a0′、a1′、a2′代入（27）式中，可以得到低渗2区的地层压力分布方程p2（r，t）。

由地层压力方程p2（r，t），可以得到t大于T0时间段内任一时刻低渗2区的平均地层压力：

由（2）式可以看出，低渗2区的外边界半径R2随着泄油半径re的变化而变化，利用物质平衡方程可得到re和R2随时间的变化规律。

物质平衡方程的表达式为：

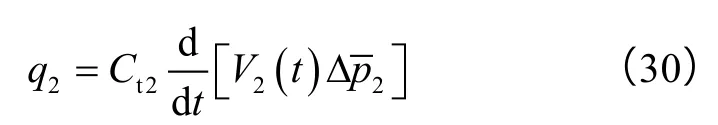
即单位时间内采出的液量等于该时间段内2区地层激动区内液体弹性储量的改变量。其中，地层激动区内的孔隙体积为：

平均压降为：

低渗2区的补给量为：

将（31）式、（32）式代入（30）式中，在t大于T0时间内，进行积分，可以得到：

将（29）式代入（34）式中，再结合（33）式，即可求得不同时刻低渗2区的外边界半径R2（t）和泄油半径re（t）值。

将p2（r，t）代入（24）式可以得到：

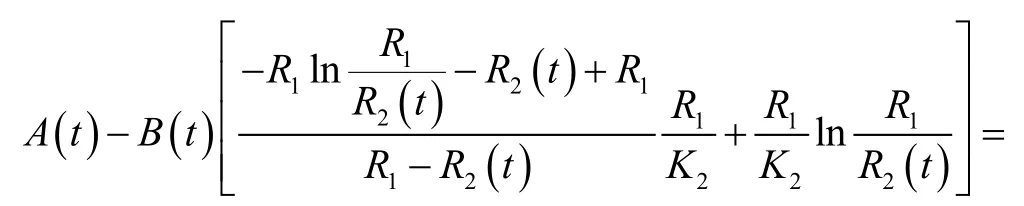
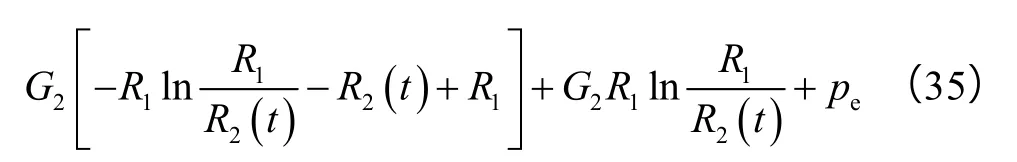
联立（21）式和（35）式可以得到A（t）和B（t）的表达式，代入（19）式和（28）式中，即可得到a0、a1、a2以及a0′、a1′、a2′的解，分别代入（18）式和（27）式中，即可得到高渗1区和低渗2区的地层压力分布方程p1（r，t）、p2（r，t）。将地层压力分布方程代入（20）式和（29）式中，可得到任一时刻各区的平均地层压力，最终用于预测各区的动态储量。

1.4 两区补给动态储量预测模型

假设压裂水平井累计产量为Np，高渗1区的动态储量为N1，低渗2区的动态储量为N2。首先由各区的平均地层压力来判定油藏类型，即是饱和还是未饱和油藏，不同类型的油藏具有不同的物质平衡方程［1，10］。

1.4.1 未饱和油藏

对于未饱和油藏，即pe大于pb或者大于pb时，只考虑弹性驱作用，高渗1区和低渗2区的物质平衡方程式分别为：

1.4.2 饱和油藏

对于饱和油藏，即pe小于等于pb或者小于等于pb时，其开发主要靠溶解气析出、膨胀所产生的驱动作用，同时考虑由于地层降压所引起的地层束缚水和地层岩石的弹性膨胀作用，高渗1区和低渗2区的物质平衡方程式分别为：

t大于T0时，低渗2区流体开始向高渗1区进行补给，其累计供给量为：

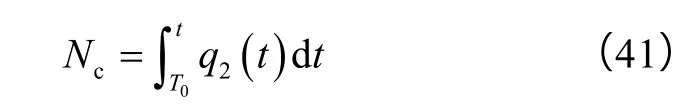
将（33）式代入（41）式中，联立前面得到的B（t）的表达式，可以得到低渗2区的累计供给量Nc的表达式。

将高渗1区和低渗2区的平均地层压力表达式代入相应的物质平衡方程中，即可得到各区的动态储量预测模型。

2 应用实例

本文以四川盆地侏罗系某致密油藏为例，进行压裂水平井单井动态储量预测。该油藏为致密灰岩油藏，储集层含油性不受构造控制，大面积含油，岩性复杂、物性差，发育多尺度孔喉系统和裂缝。受岩性、物性、裂缝影响，储集层表现出较强的非均质性。

该油藏中压裂水平井G1-H水平段长度为1 000 m，水力裂缝条数为10条，裂缝半长230 m。该井投产1年左右，初期平均日产油为19 t，目前累计产量0.36×104t。历史拟合反演参数说明，储集层为裂缝-孔隙型，天然裂缝发育，人工裂缝导流能力为0.126×10-3μm2·cm。

G1-H井储集层渗透率为0.06×10-3μm2，地层综合压缩系数1.9×10-3MPa-1，地层原油黏度0.5 mPa·s，地面原油密度0.84 g/cm3，有效厚度7.5 m，原始地层压力38 MPa，饱和压力29 MPa。

2.1 等效参数

高渗1区发育人工裂缝、天然裂缝和基质，其等效渗透率为0.93×10-3μm2，等效半径R1为382.65 m；低渗2区发育天然裂缝和基质，其等效渗透率为0.09×10-3μm2，等效半径R2是低渗2区的外边界半径，是随时间变化的非稳态值（见图3），当压力波传播到1区边界后，R2开始不断增加。

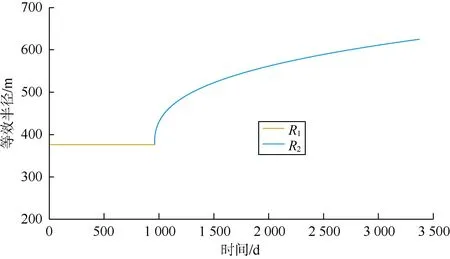
图3　G1-H井等效泄油半径随时间变化曲线

2.2 分区平均地层压力

通过历史拟合模拟产能变化规律，预测该井生产10年累产可达到1.87×104t（见图4）。结合产能变化规律，利用各区压力分布方程，得到高渗1区和低渗2区平均地层压力变化规律。由图5可见，大约生产960 d后，压力波传播到高渗1区边界，且近井的高渗1区地层压力下降较快，远井2区地层压力下降较慢。

针对G1-H井，利用其储集层、流体、压裂参数，建立双重介质单压裂水平井模型，并按照两区物质平衡法的分区标准，将单井控制范围分为两个渗流区。在对产量进行历史拟合后，模拟计算该井生产10年后的地层压力分布（见图6、图7），将数值模拟与本文模型计算结果进行对比，可见两种方法得到结果很相近。由此可见，本文将单井渗流区等效为径向渗流区的方法具有一定的可行性和准确性。

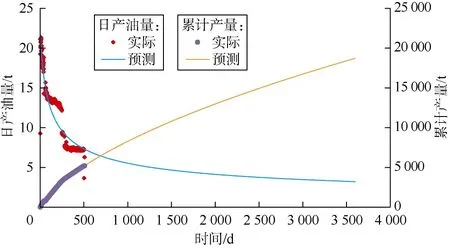
图4　G1-H井历史拟合和产能预测曲线

图5　G1-H井各渗流区平均地层压力变化曲线

图6　G1-H井生产10年后地层压力分布

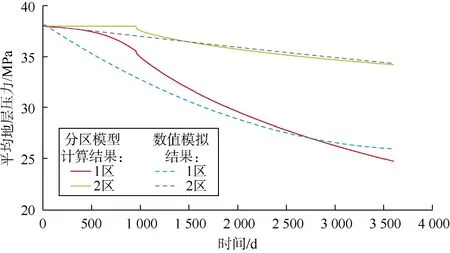
图7　本文分区模型和数值模拟计算的各区压力对比图

2.3 动态储量

根据各区每个时间步的平均地层压力判定油藏类型，利用两个渗流区在饱和与未饱和状态下的物质平衡方程，计算得到各区每个时间步下的动态储量，最终可以得出该井动态储量随时间的变化规律（见图8）及低渗2区对高渗1区的累计供给量的变化规律（见图9）。由图9可见，G1-H井生产960 d左右后，低渗2区流体向1区进行补给，其补给量不断增加，生产10年累计补给量为0.97×104t，该井生产10年动态储量预测可达到15.80×104t。

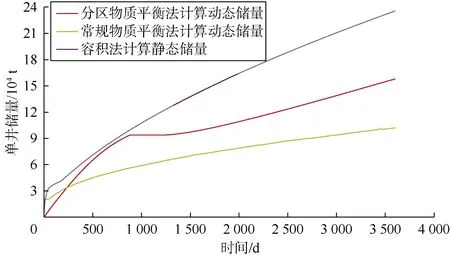
图8　G1-H井储量预测曲线对比图

图9　G1-H井低渗2区累计补给量变化曲线

本文利用常规物质平衡法计算得到G1-H井生产10年动态储量为10.20×104t。利用容积法计算单井控制范围内的静态地质储量时，G1-H井的控制面积为10条压裂缝控制的椭圆渗流区面积的叠加，且考虑了缝间干扰，由此算得该井生产10年控制储量将达到23.56×104t（见图8）。通过对比可以看出，容积法算得的是单井控制范围内的静态地质储量，而动态储量反映的是油藏中能够有效流动的原油储量，因此，容积法算得的控制储量值最大，而两区补给物质平衡法考虑了低渗区的补给和两区间的流体交换，该方法算得的动态储量比常规物质平衡法算得的值大。

综合对比可见，两区补给物质平衡法结合实际生产动态，考虑了致密油储集层的非均质性，即针对近井区和远井区储集层和渗流特征的不同，考虑了两区交界面处压力突变和流体交换，更接近实际情况，可较为准确地预测单井控制范围内的动态储量。

3 结论

针对致密油储集层非均质性强的特点，单压裂水平井的渗流区域可分为高渗1区和低渗2区，等效为径向复合渗流模型，将各区的多重介质等效为一种连续性介质，以平行板理论为基础，利用渗流力学的相关理论，建立致密储集层的等效连续介质模型，进行物性参数的等效。

基于致密油多重介质的非线性渗流机理，考虑启动压力梯度、应力敏感效应等因素的影响，分区建立相应的非线性渗流模型，考虑两类渗流区交界面处压力突变和流体交换，结合积分法，求取各区的压力分布方程，根据地层压力判定油藏类型，针对饱和与未饱和两种油藏类型，建立各区相应的物质平衡方程，联立得到致密油压裂水平井单井动态储量以及不同开采时间内低渗区对高渗区的补给量。

实例计算表明，在开发过程中，低渗区对高渗区的补给量较大，且高渗区压力比低渗区下降快。通过对比，该两区补给物质平衡法更符合致密油储集层和渗流特征，可较为准确地预测单井控制范围内的动态储量，为生产井产量及工作制度的确定、开发井网的部署和调整提供依据，实现致密油的经济有效开发。

符号注释：

a，b——实验系数；bf——天然裂缝开度，m；bF——人工裂缝开度，m；Bgi——气体体积系数；Boi——初始原油体积系数；Bo1，Bo2——1区、2区的原油体积系数；Cfi——岩石压缩系数，Pa-1；Coi——原油压缩系数，Pa-1；Cti——综合压缩系数，Pa-1；Cw——地层水的压缩系数，Pa-1；d——裂缝发育区宽度，m；DL——裂缝的线密度，m；Gi——启动压力梯度，Pa/m；h——油层有效厚度，m；Kf——天然裂缝渗透率，m2；KF——人工裂缝渗透率，m2；KF0——初始条件下裂缝渗透率，m2；Ki——渗透率，m2；Km——基质渗透率，m2；Km0——初始条件下基质渗透率，m2； L——水平段长度，m；n——裂缝条数；Nc——低渗2区对高渗1区的累计供给量，m3；Ni——动态储量，m3；Np——累计产油量，m3；pb——饱和压力，Pa；pe——原始地层压力或供给边界处压力，Pa；——低渗2区的平均压降，Pa；pi——地层压力，Pa；——平均地层压力，Pa；pw——井底流压，Pa； q——压裂水平井总流量，m3/s；q2——低渗2区对高渗1区的供给量，m3/s；r——距井轴的任意半径，m；re——供给半径，m；rw——井筒半径，m；Ri——等效泄油半径，m；Rpi——生产气油比，m3/m3；Rsi——原始溶解气油比，m3/m3；Rsi——溶解气油比，m3/m3；R（t）——压力波传播距离，m；Swi——原始含水饱和度，f；t——生产时间，s；T0——压力波传播到1区边界的时刻，s；V2（t）——2区地层激动区内的孔隙体积，m3；xF——压裂缝半长，m；αF——裂缝渗透率变形系数，Pa-1；αm——基质渗透率变形系数，Pa-1；ηi——导压系数，m2/s；μ——原油黏度，Pa·s；φf——天然裂缝孔隙度，f；φF——人工裂缝孔隙度，f；φm——基质孔隙度，f；φi——孔隙度，f。下标：i——地层分区，i=1为高渗1区，i=2为低渗2区。

参考文献：

［1］黄全华， 王富平， 尹琅， 等.低渗气藏气井产能与动态储量计算方法［M］.北京： 石油工业出版社， 2012.HUANG Quanhua， WANG Fuping， YI Lang， et al.The calculation method for gas well production and dynamic reserve of low permeability gas reservoir［M］.Beijing： Petroleum Industry Press， 2012.

［2］高承泰， 卢涛， 高炜欣， 等.分区物质平衡法在边水气藏动态预测与优化布井中的应用［J］.石油勘探与开发， 2006， 33（1）： 103-106.GAO Chengtai， LU Tao， GAO Weixin， et al.Multi-region material balance method and its use in the performance prediction and optimal well pattern design of edge water reservoir［J］.Petroleum Exploration and Development， 2006， 33（1）： 103-106.

［3］李欣， 李士伦， 刘建仪， 等.应用瞬态物质平衡法计算气藏储量［J］.天然气工业， 2002， 22（4）： 71-73.LI Xin， LI Shilun， LIU Jianyi， et al.Estimating gas reserves in a reservoir by use of transient material balance method［J］.Natural Gas Industry， 2002， 22（4）： 71-73.

［4］王卫红， 沈平平， 马新华， 等.非均质复杂低渗气藏动态储量的确定［J］.天然气工业， 2004， 24（7）： 80-82.WANG Weihong， SHEN Pingping， MA Xinhua， et al.Verification of dynamic reserves for heterogeneous complex gas reservoirs with low permeability［J］.Natural Gas Industry， 2004， 24（7）： 80-82.

［5］程时清， 杨秀祥， 谢林峰， 等.物质平衡法分区计算定容气藏动储量和压力［J］.石油钻探技术， 2007， 35（3）： 66-68.CHENG Shiqing， YANG Xiuxiang， XIE Linfeng， et al.Multi-region calculation of dynamic reserve and pressure of constant volume reservoirs using material balance［J］.Petroleum Drilling Techniques，2007， 35（3）： 66-68.

［6］陈光梅， 车雄伟.弹性驱低渗透油气藏的分区物质平衡方法［J］.新疆石油地质， 2011， 32（2）： 157-159.CHEN Guangmei， CHE Xiongwei.Domain material balance method for low permeability gas-oil reservoir by depletion drive process［J］.Xinjiang Petroleum Geology， 2011， 32（2）： 157-159.

［7］周涌沂， 车雄伟.低渗透油藏分区物质平衡方法研究［J］.西安石油大学学报（自然科学版）， 2010， 25（6）： 42-46.ZHOU Yongyi， CHE Xiongwei.Regional material balance method for low permeability reservoir［J］.Journal of Xi'an Shiyou University （Natural Science Edition）， 2010， 25（6）： 42-46.

［8］秦同洛， 李璗， 陈元千.实用油藏工程方法［M］.北京： 石油工业出版社， 1992.QIN Tongluo， LI Dang， CHEN Yuanqian.Applied reservoir engineering［M］.Beijing： Petroleum Industry Press， 1992.

［9］冯曦， 贺伟， 许清勇.非均质气藏开发早期动态储量计算问题分析［J］.天然气工业， 2002， 22（增刊）： 87-90.FENG Xi， HE Wei， XU Qingyong.Discussion on calculating dynamic reserves in the early stage of heterogeneous gas reservoir development［J］.Natural Gas Industry， 2002， 22（Supp.）： 87-90.

［10］吴奇， 胥云， 王晓泉， 等.非常规油气藏体积改造技术： 内涵、优化设计与实现［J］.石油勘探与开发， 2012， 39（3）： 352-358.WU Qi， XU Yun， WANG Xiaoquan， et al.Volume fracturing technology of unconventional reservoirs： Connotation， optimization design and implementation［J］.Petroleum Exploration and Development， 2012， 39（3）： 352-358.

［11］吴奇， 胥云， 张守良， 等.非常规油气藏体积改造技术核心理论与优化设计关键［J］.石油学报， 2014， 35（4）： 706-714.WU Qi， XU Yun， ZHANG Shouliang， et al.The core theories and key optimization designs of volume stimulation technology for unconventional reservoirs［J］.Acta Petrolei Sinica， 2014， 35（4）： 706-714.

［12］MAYERHOFER M J， LOLON E P， WARPINSKI N R， et al.What is stimulated reservoir volume （SRV）？［R］.SPE 119890， 2008.

［13］MONGALVY V， CHAPUT E， AGARWAL S， et al.A new numerical methodology for shale reservoir performance evaluation［R］.SPE 144154， 2011.

［14］付玉， 代雪梅， 李涧松， 等.等效连续介质模型在低渗透油藏的适应性分析［J］.西南石油大学学报（自然科学版）， 2010， 32（3）： 93-96.FU Yu， DAI Xuemei， LI Jiansong， et al.Adaptability analysis of the equivalent continuum media model on fractured low permeability reservoir［J］.Journal of Southwest Petroleum University（Science & Technology Edition）， 2010， 32（3）： 93-96.

［15］刘永辉.缝洞型碳酸盐岩油藏渗透率等效计算方法研究［D］.青岛：中国石油大学（华东）， 2010.LIU Yonghui.The research of equivalent permeability calculation for fractured-vuggy carbonate reservoir［D］.Qingdao： China University of Petroleum （East China）， 2010.

［16］徐轩， 杨正明， 祖立凯， 等.多重介质储层渗流的等效连续介质模型及数值模拟［J］.断块油气田， 2010， 17（6）： 733-737.XU Xuan， YANG Zhengming， ZU Likai， et al.Equivalent continuous medium model and numerical simulation of multimedia reservoir［J］.Fault-Block Oil & Gas Field， 2010， 17（6）： 733-737.

［17］徐轩， 杨正明， 刘先贵， 等.缝洞型碳酸盐岩油藏的等效连续介质模型［J］.石油钻探技术， 2010， 38（1）： 84-88.XU Xuan， YANG Zhengming， LIU Xiangui， et al.The equivalent continuum media model for fractured cavernous carbonate reservoir［J］.Petroleum Drilling Techniques， 2010， 38（1）： 84-88.

［18］冯金德， 程林松， 李春兰， 等.裂缝性低渗透油藏等效连续介质模型［J］.石油钻探技术， 2007， 35（5）： 94-97.FENG Jinde， CHENG Linsong， LI Chunlan， et al.Equivalent continuous medium model for fractured low-permeability reservoir［J］.Petroleum Drilling Techniques， 2007， 35（5）： 94-97.

［19］戈尔布诺夫 A T.异常油田的开发［M］.张树宝， 译.北京： 石油工业出版社， 1987.GORBUNOV A T.Abnormal oilfield development［M］.ZHANG Shubao， Trans.Beijing： Petroleum Industry Press， 1987.

［20］巴斯宁耶夫 K C.地下流体力学［M］.张永一， 赵碧华， 译.北京：石油工业出版社， 1992.BASNYEV K C.Underground hydrodynamics［M］.ZHANG Yongyi，ZHAO Bihua， Trans.Beijing： Petroleum Industry Press， 1992.

［21］巢华庆， 王玉普.复杂油藏试井技术［M］.北京： 石油大学出版社， 2001.CHAO Huaqing， WANG Yupu.Complex well testing technology［M］.Beijing： China University of Petroleum Press， 2001.

［22］刘能强.实用现代试井解释方法［M］.北京： 石油大学出版社， 2010.LIU Nengqiang.Practical modern well testing interpretation method［M］.Beijing： China University of Petroleum Press， 2010.

（编辑 张敏）

Determination of dynamic reserves of fractured horizontal wells in tight oil reservoirs by multi-region material balance method

WEI Yi1， 2， RAN Qiquan1， 2， LI Ran1， 2， YUAN Jiangru1， 2， DONG Jiaxin1， 2
（1.National Energy Center of Tight Oil and Gas， Beijing 100083， China； 2.PetroChina Research Institute of Petroleum Exploration & Development， Beijing 100083， China）

Abstract：To overcome the deficiencies of the material balance method， according to strong heterogeneity of tight oil reservoirs， the flow region of fractured horizontal well is divided into high permeable zone and low permeable zone， which are equivalent to radial composite percolation model.Based on parallel plane theory， multiple media of each zone are equivalent as a continuous medium， and with the integral method， the multi-region material balance to calculate the dynamic reserves for the fractured horizontal well of tight oil reservoirs is proposed base on the nonlinear seepage mechanism of tight oil reservoirs， and the corresponding pressure distribution equation and material balance equation for the two zones have been established.In view of the actual production performance， this method considers the pressure mutation and fluid exchange at the interface of two zones.The computational results of an example show that this method can work out the dynamic reserves within a single well control， the dynamic reserves of high permeable zone and low permeable zone， and the recharge rate from the low permeable zone to the high permeable zone in different production time accurately， which provides a basis for selection of well production and appropriate working system， and deployment and adjustment of development well pattern.

Key words：tight oil； fractured horizontal well； pressure distribution； dynamic reserves； multi-region； material balance method

中图分类号：TE331.1

文献标识码：A

文章编号：1000-0747（2016）03-0448-08

DOI：10.11698/PED.2016.03.16

基金项目：国家高技术研究发展计划（863计划）“致密砂岩油气藏数值模拟技术与软件（2013AA064902）；中国工程院咨询研究项目“中国致密油发展战略研究”（gg-zd-2）

第一作者简介：魏漪（1980-），女，湖北潜江人，博士，中国石油勘探开发研究院博士后，主要从事超低渗透、致密油气藏开发及渗流力学理论方面的研究工作。地址：北京市海淀区学院路20号，中国石油勘探开发研究院油气开发软件中心，邮政编码：100083。E-mail：weiyi1980@petrochina.com.cn

收稿日期：2015-06-12 修回日期：2016-03-25