西北太平洋海洋温度锋生与锋消机制的初步研究
赵 宁, 韩 震, 2, 刘贤博(. 上海海洋大学 大洋渔业资源可持续开发省部共建教育部重点实验室, 上海 20306; 2. 上海海洋大学 海洋科学学院, 上海 20306)
西北太平洋海洋温度锋生与锋消机制的初步研究
赵 宁1, 韩 震1, 2, 刘贤博1
(1. 上海海洋大学 大洋渔业资源可持续开发省部共建教育部重点实验室, 上海 201306; 2. 上海海洋大学 海洋科学学院, 上海 201306)
海洋锋面区域对气候变化以及海气耦合作用的影响非常显著, 通过分析其形成机制, 可以帮助进一步了解海洋与大气的相互作用过程以及其物理过程。利用Argo数据、NCEP/NCAR再分析数据和遥感风场数据对西北太平洋的混合层温度与温度锋面的变化机制进行了研究。基于海洋混合层的热量收支模型, 发现在北太平洋区域的海洋混合层温度主要受到净热通量控制, 同时还存在一个季节变化明显的温度锋面。9~2月为温度锋面加强时期, 3~4月温度锋面变化不明显, 而5~8月温度锋面则迅速减弱。根据研究, 该温度锋面的加强与减弱主要是由于净热通量的南北差异造成的, 而在净热通量中则以短波辐射通量与潜热通量为主要影响因子。
西北太平洋; 海洋混合层; 海洋温度锋; 锋生; 锋消
[Foundation: Satellite Based High-tech Industrialization Demonstration Project of National Development and Reform Commission, No. 2009214;National Science & Technology Pillar Program, No. 2013BAD13B00]
海气交界面的热量交换对气候变化与海气耦合作用有着至关重要的影响。早期的海洋的热量收支研究通常采用一维模型[1-2]。Qiu与Kelly[3]在研究中,建立了二维的混合层模型, 其中平流项由艾克曼平流与地转流构成。Moisan与Niiler[4]则在研究中利用连续性方程与热量守恒方程推导出了混合层垂向平均的二维热量收支方程。2004年, Dong和Kelly[5]在研究中改进了Qiu与Kelly[3]在1993年引入的二维混合层模型, 并评估了墨西哥湾流区域的热量收支情况, 结果表明在受到湾流影响的区域, 相较于净热通量, 地转流对混合层的热量收支影响更大。
海洋温度锋是海洋中不同水团之间海水温度急剧变化的区域。大面积的海洋锋面区域通常被认为是海洋表层动量与热通量驱动所致[6]。20世纪80年代早期, 研究者们利用遥感数据, 开展了对大面积海域的海洋锋研究[7-8]。锋面的判断标准通常会根据研究区域的不同而有所不同, 如Kazmin与Rienecker[6]采用的以及Park等[9]采用的等。考虑到锋面的变化通常与海表层的动量与热通量相关,Kazmin与Rienecker[6]利用了一个简化的混合层模型来分析锋面强度的变化机制。Qiu与Kawamura[10]在对北太平洋温度锋消研究中也提到了需用混合层模型来对温度锋生与锋消机制的进行定量研究。目前,对海洋温度锋的研究大多集中于锋面的时空变化,而对锋面的锋生与锋消机制研究还较少。因此, 本研究以Argo数据、NCEP/NCAR再分析数据以及遥感风速数据为基础, 建立海洋混合层热量收支方程,对西北太平洋海域内海洋混合层热量收支以及海洋温度锋变化机制进行了研究。
1 数据与方法
1.1 数据
本文选取的数据为国际太平洋研究中心/亚太数据研究中心(International Pacific Research Center/Asia-Pacific Data-Research Center)提供的2005~2012年的Argo历史数据(Climatology dataset)、美国环境预报中心(NCEP)和国家大气研究中心(NCAR)联合开发的NCEP/NCAR再分析数据以及Remote Sensing Systems组织提供的QuikScat/Ascat卫星遥感风场数据。
Argo历史数据中包含了月平均的海水温度与盐度数据(水平分辨率为1°×1°、垂向为27层)。而NCEP/NCAR再分析数据为日平均数据且采用了不等距的高斯网格。因此, 在计算时, 我们利用双样条线性插值法, 将再分析数据以及风场数据插值到1°×1°网格上。最后, 将所有数据按月进行长年平均,得到最终的月平均数据。
1.2 研究区域
我们选择的研究区域为西北太平洋开阔的大洋区域(135°~170°E, 15°~35°N)。该区域存在两股洋流系统, 分别为黑潮续流(Kuroshio Extension)与亚热带逆流(Subtropical Countercurrent), 并形成了一个存在明显季节性变化的温度、密度锋面, 称为亚热带锋(Subtropical Front)[11-12]。
混合层的判定方法有很多, 依据研究目的不同而分类众多, 可以大致分为: 梯度法、温度差法与密度差法等[13-15]。本研究采用基于动态密度差的混合层深度(Mixed Layer Depth, MLD)判别法。密度差可以通过下式给出:

其中,T=s–1000为基于温度计算的密度; T为参考深度的温度(10 m); ΔT为给定的温度差值(本研究取0.5℃); S为参考深度的盐度, P为压力(取0), ρs为海水密度。各区域的混合层所在深度的密度可通过MLD=MLD–计算得出。此外, 我们根据混合层的性质, 假设海水在混合层中处于充分混合的状态,因此混合层温度(Mixed Layer Temperature, MLT)可以由混合层内的海水温度的垂向平均值表示。
通过选取1月、4月、7月与10月作为4季的代表月份, 图1表示了研究区域的混合层温度以及混合层深度的季节性变化。我们发现该区域混合层深度较浅, 年间深度均小于100 m。冬、春两季, 研究区域的北部与南部的混合层深度均较中部区域深,夏、秋两季则显示出北浅南深的现象。
由于地处亚热带区域, 该区域的全年混合层温度都较高, 且大部分区域的温度大于20℃。冬、春两季, 在20°~30°N之间, 混合层温度随纬度的变化梯度很大(即, 温度锋面), 而在夏、秋两季并不明显。根据研究区域温度大致沿纬度变化, 南高北低, 故可利用下式计算温度锋面的强度(Gradient Magnitude, G):

图2给出了西北太平洋的温度锋面的时空分布。该温度锋面从10~11月开始, 在北部出现, 锋面强度约为0.4℃/100km。同时, 锋面存在着西低东高的空间分布状态。在之后的冬季与春季间, 该锋面逐渐加强, 强度超过0.4℃/100km的区域扩大到20°N以北的整个西北太平洋海域。6月份, 锋面面积最大, 中心强度超过0.8℃/100km; 随后迅速消失。
1.3 方法
1.3.1 混合层模型
在研究海洋上层温度变化时, 混合层温度变化模型是较为常用的研究方法之一。通过对海洋混合层的热量收支进行分析, 我们可以进一步分析海洋温度锋面的生消机制。我们所采用的模型, 可以通过下式表示[6, 16]:
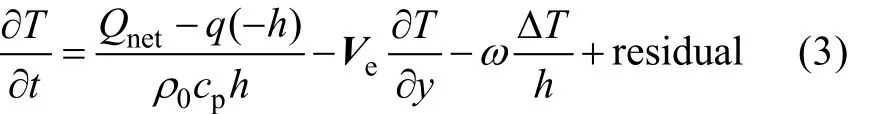
其中, T与h分别为混合层温度与混合层深度; ρ0为海水密度(1.025×103kg/m3); cp为常压下的海水比热(3 998 J/(kg·℃)); Qnet为海表面的净热通量, 可以通过下式计算:

其中, Qsw为短波辐射, Qlw为长波辐射, Qsh为显热通量, Qlh为潜热通量, 正值代表海洋获得热量。
各热通量可通过经验公式进行计算。短波辐射热通量可由公式(5)给出:
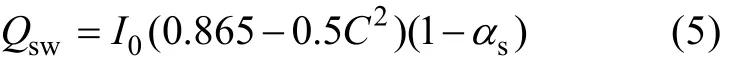
其中, I0为晴天的太阳辐射, C为云量,s为海面反射率(本文取0.06[7])。其他热通量, 我们参考了Kim[17]与Park等[18]在研究中提出的公式, 分别进行了计算:
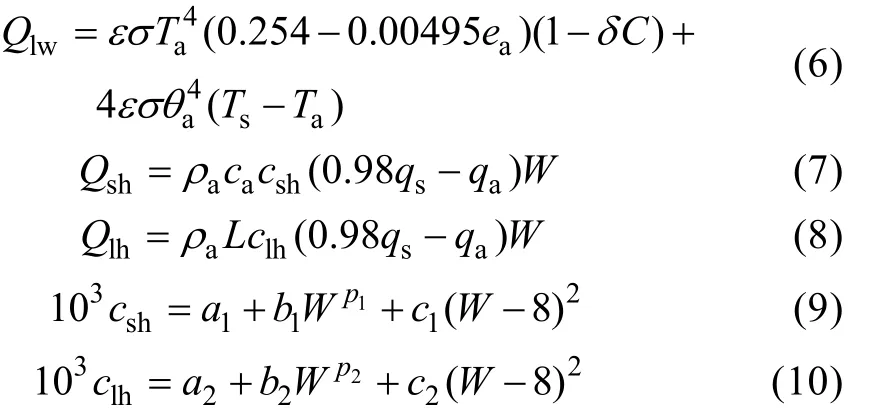
其中, 为辐射率(0.97); 为斯忒藩-波兹曼常数(5.67×10–8W/(m2·K4)); ea为水蒸汽压; 为云参数, 由式(11)计算得到[19-20];a为气温(单位为K); Ts和 Ta分别为海水温度与气温(单位为℃);a为空气密度,由式(12)计算; ca为常压下的空气比热(1 005 J/(kg·K));W为海表风速; L为蒸发潜热(2.5×106J/kg); qs为海表温度下的饱和比湿度(考虑到盐度影响, 取0.98[21]),qa为空气比湿; 其他为系数[22]。
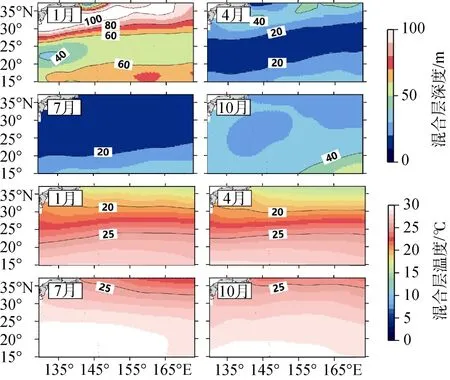
图1 西北太平洋海域的混合层深度与温度分布Fig. 1 Map of the mixed layer depth and temperature in the study region
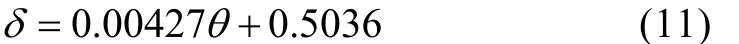
其中, 为纬度。
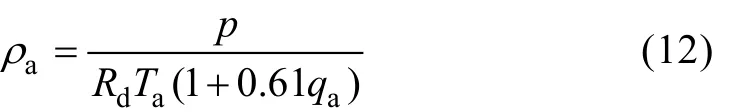
其中, p为海表气压; Rd为干燥空气气体常数(287 J/(kg·K))。
公式(1)中的q(–h)为混合层底部的穿透辐射通量, 可以通过下式计算:
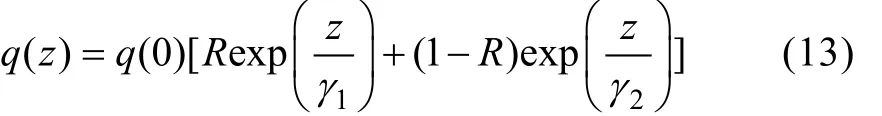
其中, q(0)为海表面的短波辐射通量; R、1和2与水质有关, 这里我们取R为0.58,1为0.35,2为23, 代表I类水体[23]。
公式(3)的右边第三项为艾克曼平流项, 艾克曼流矢量Ve可通过下式计算:
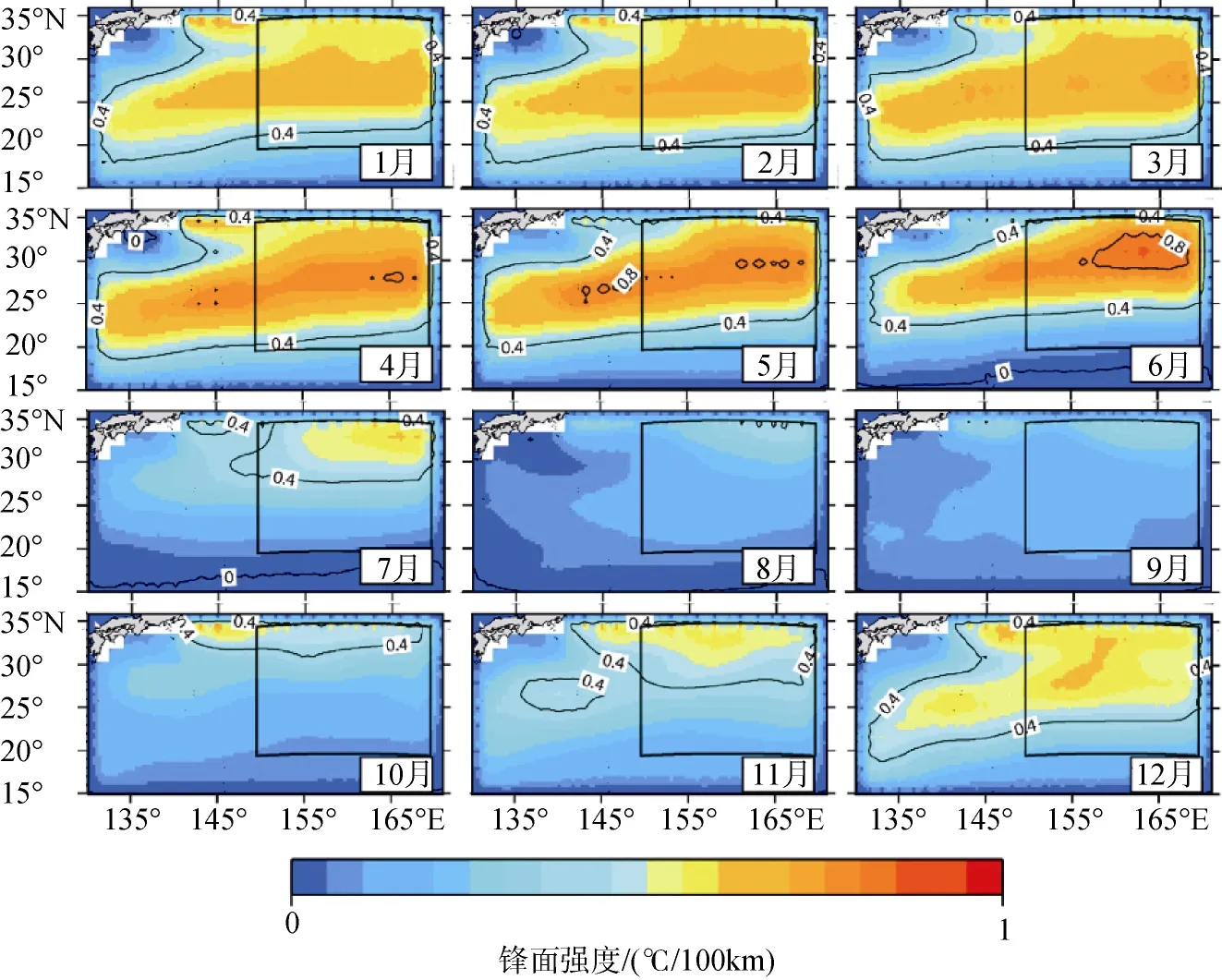
图2 研究区域的锋面强度Fig. 2 Gradient magnitude of the front in the study region

其中,x为经向风应力, f为科氏力参数。
第四项为混合层底部的卷吸项。ΔT表示混合层与混合层以下区域的温度差, 垂向速度由垂向风应力旋度curl算出:
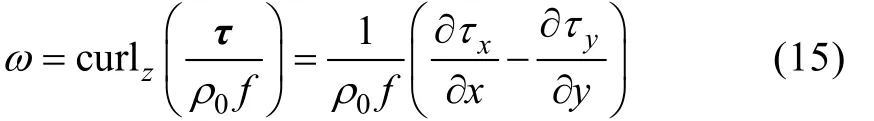

其中, U为10 m风速矢量; CD为阻力系数, 通过下式计算:
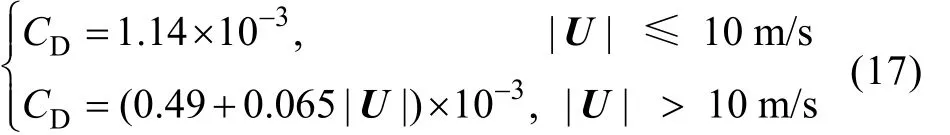
最后一项为残差项(residual), 包括方程内没有考虑到的因素, 如: 地转平流项、扩散项等。
1.3.2 锋面强度模型
由于我们定义锋面强度由公式(2)给出, 因此,锋面强度的时间变化方程可通过对公式(3)进行经向微分得到:

其中, 最后一项(residual’)为锋面强度方程本身的残差项。
2 结果
2.1 混合层模型
根据公式(3), 我们评估了研究区域内的混合层热量收支情况。图3显示了研究区域内的混合层温度时间变化趋势。
在研究区域内, 混合层温度从3月开始升高; 升温趋势在6、7月间达到最大, 且北部升温较南部明显; 8月间大部分区域混合层温度达到峰值, 同时西南区域温度开始回落; 9月至2月间, 混合层温度总体上属于降低趋势, 北部区域较南部降温更加明显。
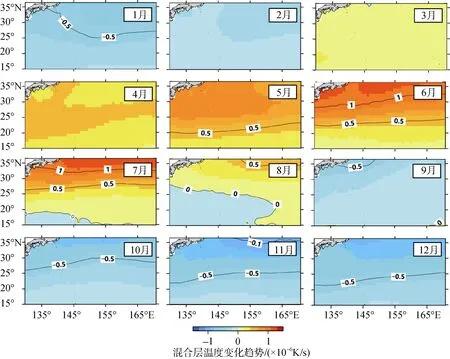
图3 研究区域的混合层温度变化趋势Fig. 3 Tendency of the mixed layer temperature in the study region
通过进一步对混合层模型中的其他项进行计算,我们得到了方程各项的贡献值。首先, 我们对方程的残差项进行了分析, 如图4。在研究区域的150°E以西区域的残差相对较大, 部分月份内该区域残差大于±0.5×10–6K/s。Hosoda[24]在研究中指出, 在受到黑潮续流影响的区域, 地转平流的贡献较净热通量多。而我们在混合层模型中仅仅考虑到了艾克曼平流项,而对地转流平流项则没有考虑。这可能是模型结果(公式(3)右边项之和)不同于实际值(公式(3)左边项)的主要原因。因此, 在以下的研究中, 我们以150°E为界, 如图2中方框所示。图5展示了方框内的各项时间变化。
根据图5, 可以看出该区域内的混合层温度变化在全年大部分时间主要受到净热通量项的影响且贡献率超过80%, 这与以往研究结果相近[4-5]。在夏季与秋季, 还受到诸如地转流等其他未知因素影响, 但净热通量贡献率依然超过60%。我们进一步分析了各热通量的贡献。结果表明, 在全年的大部分时间中, 净短波辐射贡献较大, 6月达到最大, 最大值出现在约20°~24°N, 160°~170°E区域附近, 达260 W/m2(图未给出), 而对混合层温度的影响最大超过4.3×10–6K/s。这主要是由于研究区域地处亚热带, 太阳辐射较强。净长波辐射于7月份达最大值, 对混合层温度影响最大约为–1.7×10–6K/s。相对于短波辐射与长波辐射, 潜热通量项所占比例较低, 最大值仅约为–1.1×10–6K/s。显热项与其他三项相比很小, 4月中约为–0.17×10–6K/s, 其他月份均在–0.12×10–6K/s左右。
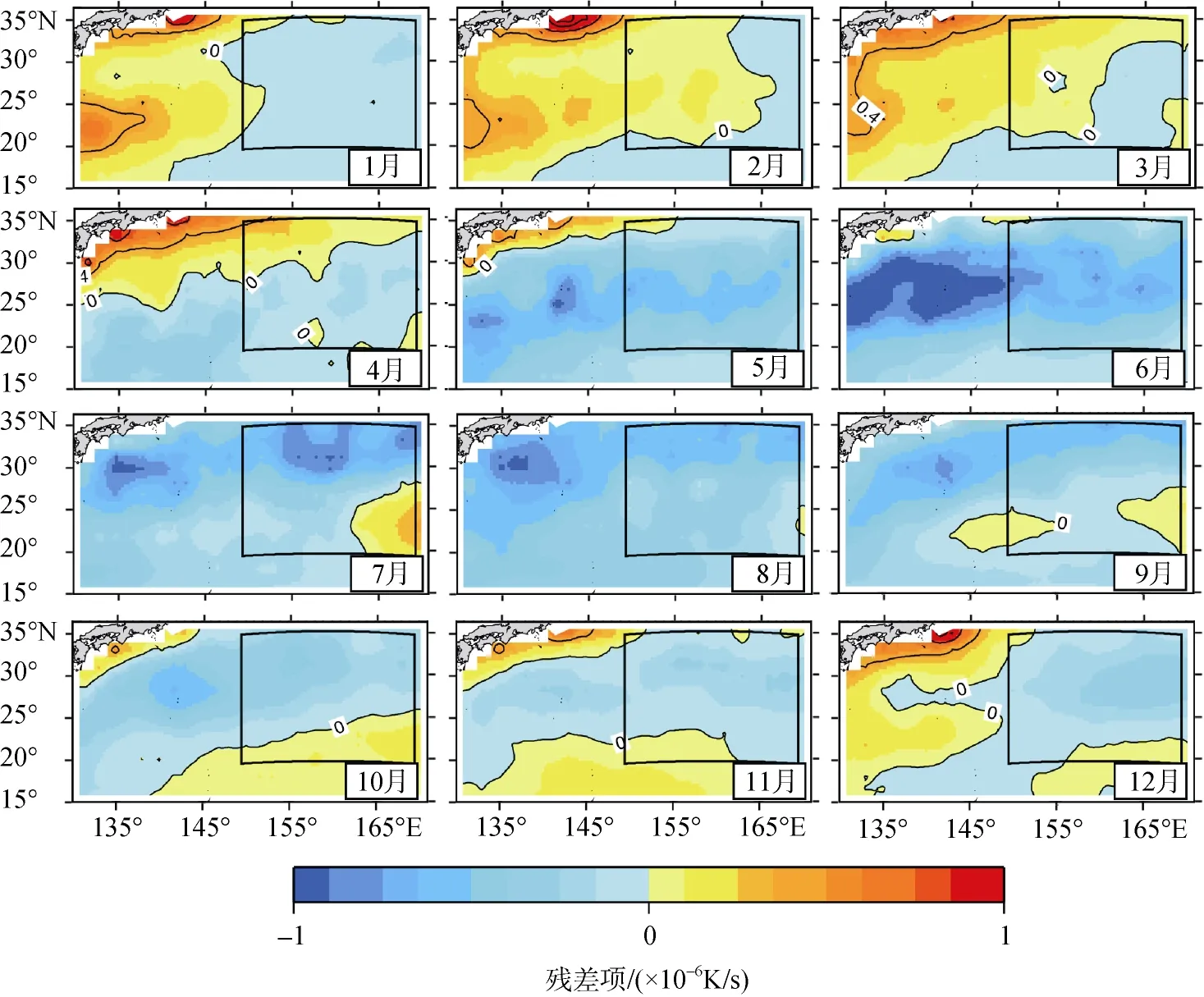
图4 公式(3)的残差项分布图Fig. 4 Horizontal map of the residual term of Equation (3) in the study region
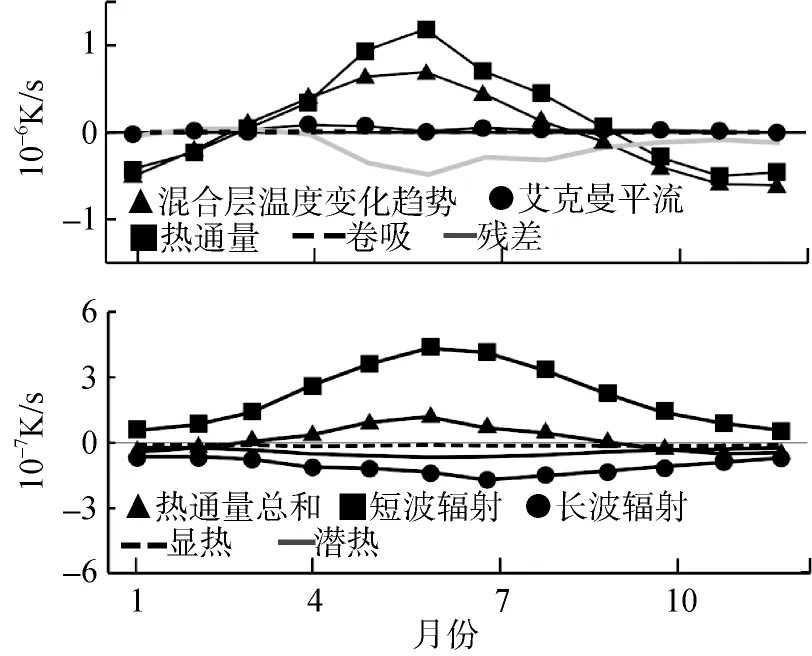
图5 混合层模型各项与净热通量各组成部分的时间变化Fig. 5 Temporal variations of the area averaged terms and heat fluxes
2.2 锋面强度模型
图6为锋面强度变化的水平分布图。我们发现, 9月开始, 锋面首先在约25°N以北160°E以西的区域开始加强; 10月向西向南扩展到几乎覆盖整个研究区域; 11月与12月锋面强度变化区域向南移动, 中心区域达到约25°N附近。其中, 10~11月锋面强度达到最高, 中心强度变化超过0.6×10–7K/(s·100km)。至1月时, 锋面有所减弱, 中心区域略向东移; 随后的2~4月, 强度变化继续降低; 5月, 南部区域锋面首先开始减弱; 6月开始, 整个海域锋面加强基本消失; 6~8月锋面迅速减弱, 直至消失。其中, 在7月间, 锋面强度减弱程度最大, 25°N附近的最大值约–1×10–7K/(s·100km)。
从总体上看, 锋面仅在5~8月减弱, 但幅度较大;9~2月, 锋面加强; 3~4月, 锋面变化较小。Qiu与kawamura[10]也在研究中提到西北太平洋区域的温度锋面在7、8月间锋面强度有大幅度减弱的现象。为了进一步了解锋面变化的具体物理机制, 我们通过公式18, 对锋面强度方程的各项进行了评估计算。
Kazmin与Rienecker[6]在对全球大洋的进行的温度锋的研究中, 曾提出影响北太平洋的温度锋生锋消的主要因素为净热通量。我们的研究结果进一步表明, 在全年的大部分时间内, 海洋温度锋面强度变化的确受到净热通量的控制, 尤其是锋面加强的9~2月与锋面减弱的5~8月。与图5不同的是, 尽管短波辐射依然占有重要的贡献比率, 然而潜热所占比重却相对提高了。从1月~5月, 短波辐射南高北低。潜热通量则北高南低, 即南部水汽蒸发较北部强。
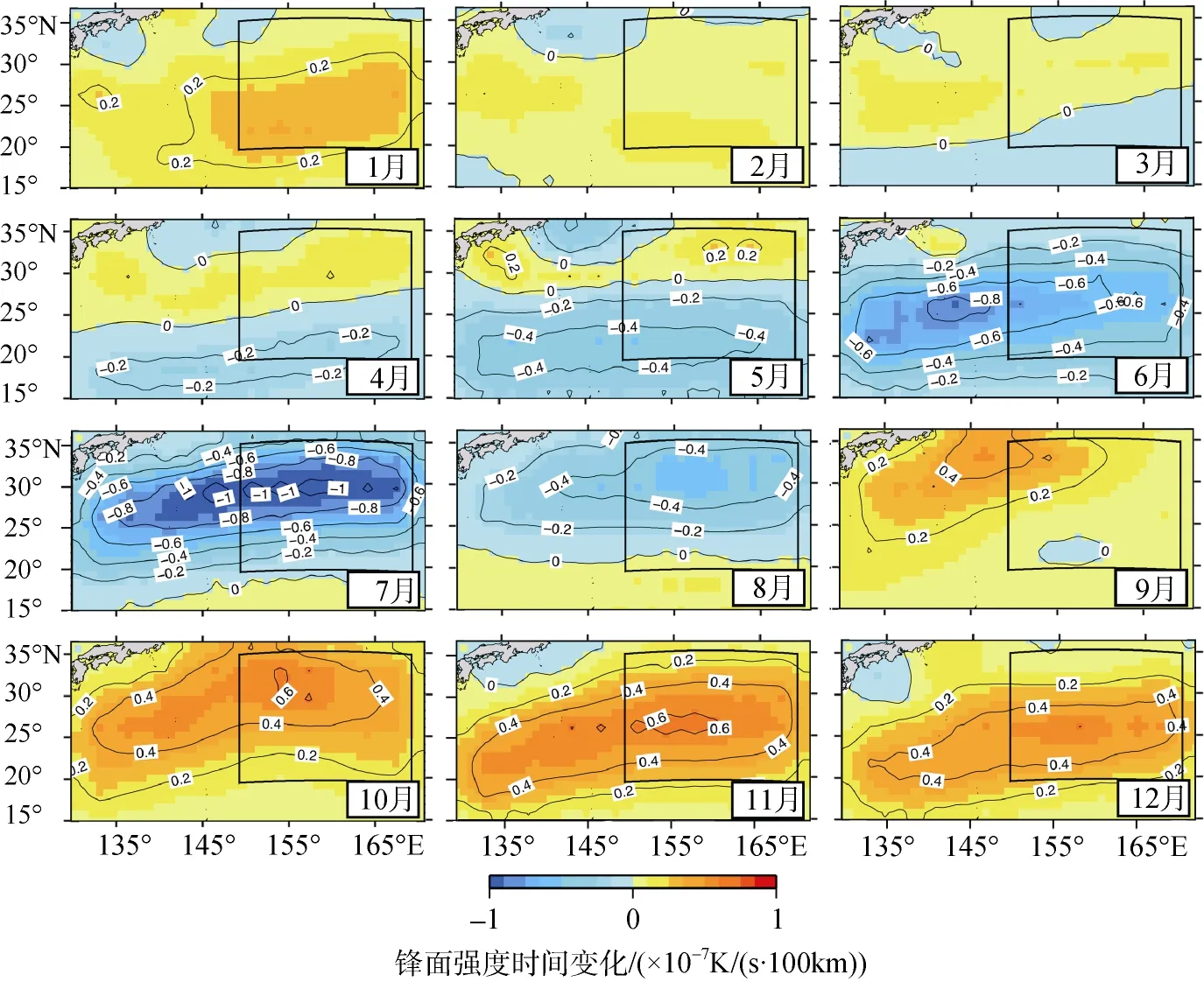
图6 锋面强度时间变化的空间分布Fig. 6 Spatial distribution of the tendency of gradient magnitude
在进入北半球的夏季以后, 短波辐射通量的南北差异开始减小, 8月份达到最低, 约–1.7×10–7K/(s·100km)。它与潜热项的共同作用在7月达到最低值(图7), 这是锋面迅速消失的主要原因。图8给出了8月份的短波辐射通量、潜热通量与混合层深度的水平分布。太阳直射点北移, 使得北部的短波辐射通量升高, 甚至高于南部, 30°N附近的短波辐射超过到230 W/m2。而潜热通量依然是北部热量损失低于南部, –100W/m2等值线在130°E区域内处在22°N左右。但是, 其随着经度向东等值线逐渐向北偏移, 至170°E区域时,等值线已位于30°N附近。根据公式(8), 我们知道潜热通量的主要影响因子为风速以及饱和比湿。而饱和比湿qs是由下式进行计算:
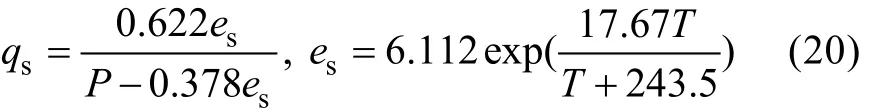
其中, es为饱和水蒸汽压, T为温度(此处为海表温度),P为海表面气压。由此, 潜热通量的水平分布实际上是受控于海气温差[12]以及西北太平洋季风[25-26]。
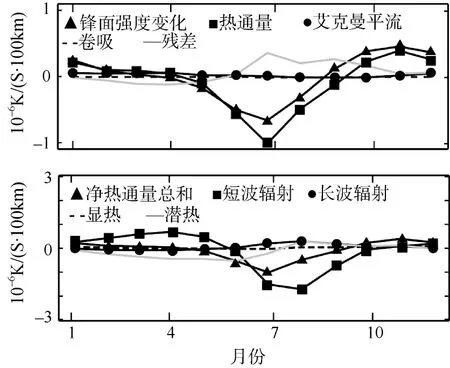
图7 锋面强度模型中各项与净热通量各组成部分的时间变化Fig. 7 Temporal variations of the terms in Eq.18 and the net heat fluxes
除了短波辐射和潜热通量, 其他热通量的影响较小。其中, 长波辐射的贡献仅在8月较大, 约为0.3×10–7K/(s·100km)。但由于8月间短波辐射的影响最为明显, 因此实际上其贡献可以忽略。
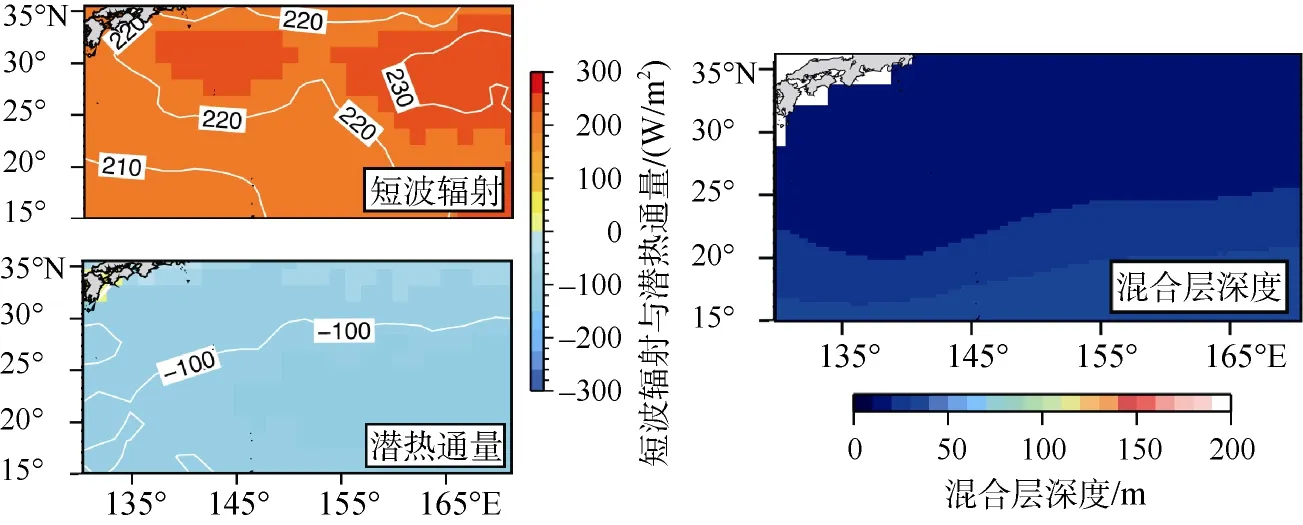
图8 8月短波辐射通量、潜热通量与混合层深度水平分布Fig. 8 Shortwave radiation flux, latent heat flux and the mixed layer depth in August
通过对区域平均结果与水平分布图的分析, 我们发现基于混合层模型的锋面强度方程评估的与实际根据混合层温度分布得到的锋面强度变化还有所差距。Kobashi等[12]与Niiler等[27]的研究表明, 在30°N以北区域, 尤其是在日本沿岸附近主要受到黑潮续流的影响, 而在120°~170°E, 20°~25°N的区域也存在着纬向地转流。同时, Kobashi等[12]在研究中提到, 该纬向地转流与区域内的海洋锋面分布具有较高的联系。因此, 我们认为在研究中忽略的地转流项是误差形成的主要原因。但考虑到误差相对于控制因子(净热通量)较小, 我们的结论仍然是可信的。
3 结论
本研究中, 我们采用基于Argo浮标的历史数据集、遥感风场数据以及再分析数据, 并应用海洋混合层模型, 重点对西北太平洋区域150°E以东内的混合层热量收支与海洋温度锋面的锋生与锋消机制进行了研究。
根据研究, 西北太平洋海域150oE以东的海域内, 混合层温度变化以及锋面的锋生与锋消现象主要是受到了热通量以及其南北差异的影响。5月开始, 太阳直射点的北移使得北部区域获得的热量开始大于南部。6月, 短波辐射总量达到最高, 最大值超过260 W/m2,而8月南北差异达到最大, 达–1.7×10–7K/(s·100km)。同时, 受夏季西南季风与洋流等的影响, 蒸发等损失的热量南北差异较小, 而北部混合层深度较南部浅,这导致北部区域混合层海水温度升温较南部快, 温度锋面逐渐减弱, 直到9月完全消失。10月开始, 伴随着北半球进入秋冬季, 并受到冬季西北季风影响,西北太平洋的北部区域热量损失相对较大, 而获得热量却较小, 北部区域降温幅度较南部更大。11月,北部部分区域的温度变化超过–1×10–6K/s, 而南部则小于–0.5×10–6K/s, 温度锋面由此形成。12月, 南北变化差异的减小, 使得锋面加强程度逐渐减弱,至2月间锋面强度趋于平稳, 其变化逐渐消失。3~4月间, 尽管南部通过短波辐射获得热量较多, 但热量损失也较北部多, 锋面变化并不明显。
在研究中, 我们发现混合层模型的解析结果仍不能完全解释实际情况。通过分析, 我们发现误差的出现主要与我们采用的混合层模型所忽略的项有关,尤其是地转流平流项[5, 12]。对于地转平流项的计算,可由地转流平衡方程推出[28], 而所需参数则可通过卫星高度计数据得到。同时, 根据以往的研究[24, 28-29],我们也发现不同的时间尺度、气候异变以及混合层的判定会对区域内的热量收支平衡造成影响。因此,在今后的研究中, 我们将针对不同时间尺度, 分别进行计算与分析, 并进一步深入地讨论气候变化与海气耦合造成的热量收支问题, 同时优化方程组成(如加入地转平流项等)。
[1] Davis R E, de Szoeke R, Niiler P. Variability in the upper ocean during MILE. Part II: Modeling the mixed layer response[J]. Deep-Sea Res, 1981, 28: 1453-1475.
[2] Niiler P P, Kraus E B. One-dimensional models of the upper ocean[C]. Kraus E B. Modelling and Prediction of the Upper Layers of the Ocean. Oxford: Pergamon Press, 1977: 152-172.
[3] Qiu Bo, Kelly K A. Upper ocean heat balance in the Kuroshio Extension region[J]. J Phys Oceanogr, 1993,23: 2027-2041.
[4] Moisan J R, Niiler P P. The seasonal heat budget of the North Pacific: net heat flux and heat storage rates (1950-1990)[J]. J Phys Oceanogr, 1998, 28: 401-421.
[5] Dong Shenfu, Kelly K A. Heat budget in the Gulf Stream region: the importance of heat storage and ad-vection[J]. J Phys Oceanogr, 2004: 34: 1214-1231.
[6] Kazmin A S, Rienecker M M. Variability and frontogenesis in the large-scale oceanic frontal zones[J]. J Geophys Res, 1996, 101: 907-921.
[7] Roden G I. On the variability of surface temperature fronts in the Western Pacific, as detected by satellite[J]. J Geophys Res, 1980, 85: 2704-2710.
[8] Kazmin A S, Legeckis R, Fedorov K N. Equatorial waves in the temperature field of the ocean surface according to shipboard and satellite measurements[J]. Sov J Remote Sens, 1985, 4: 707-714.
[9] Park K A, Ullman D S, Kim K, et al. Spatial and temporal variability of satellite-observed subpolar front in the East/Japan Sea[J]. Deep-sea Res I, 2007, 54:453-470.
[10] Qiu Chunhua, Kawamura H. Study on SST front disappearance in the subtropical North Pacific using microwave SSTs[J]. J Oceanogr , 2012, 68: 417-426.
[11] Qiu Bo, Chen Shuiming. Variability of the Kuroshio Extension jet, recirculation gyre, and mesoscale eddies on decadal time scales[J]. J Phys Oceanogr, 2005,35(11): 2090-2103.
[12] Kobashi F, Mitsudera H, Xie Shangping. Three subtropical fronts in the North Pacific: Observational evidence for mode water-induced subsurface frontogenesis[J]. J Geophys Res, 2006, 111, C09033, doi: 10.1029/ 2006JC003479.
[13] Thomson R E, Fine I V. Estimating mixed layer depth from oceanic profile data[J]. J Atmos Ocean Technol,2003, 20: 319-329.
[14] Levitus S. Climatological atlas of the world ocean [R]. NOAA Professional Paper 13, Rockville: US Gov Printing Office, 1982.
[15] Kara A B, Rochford P A, Hurlburt H E. Mixed layer depth variability over the global ocean[J]. J Geophys Res, 2003, 108, 3079, doi: 10.1029/2000JC000736, C3.
[16] de Ruijter W P M. Effects of velocity shear in advective mixed-layer models[J]. J Phys Oceanogr, 1983, 13:1589-1599.
[17] Kim Y S. Estimate of heat transport across the sea surface near Japan with bulk methods[D]. Tokyo: Univ of Tokyo, 1992.
[18] Park S, Deser C, Alexender M A. Estimation of the surface heat flux response to sea surface temperature anomalies over the global oceans[J]. J Climate, 2005,18: 4582-4599.
[19] Budyko M I. Climate and Life[M]. New York: Academic Press, 1974.
[20] Berliand M E, Berliand T G. Determining the net long-wave radiation of the earth with consideration of the effect of cloudiness[J]. Izv Akad Nauk SSSR Ser Gepfiz, 1952, 1: 64-78.
[21] Kraus E B. Atmosphere-Ocean Interaction[M]. Oxford:University Press, 1972.
[22] Kondo J. Air-sea bulk transfer coefficients in diabatic conditions[J]. Bound Layer Meteor, 1975, 9: 91-112.
[23] Paulson C A, Simpson J J. Irradiative measurements in the upper ocean[J]. J Phys Oceanogr, 1997, 16: 25-38.
[24] Hosoda K. Local phase relationship between sea surface temperature and net heat flux over weekly to annual periods in the extratropical North Pacific[J]. J Oceanogr, 2012, 68: 671-685.
[25] 王慧, 丁一汇, 何金海.西北太平洋夏季风的气候学研究[J]. 气象学报, 2005, 63(4): 418-430. Wang Hui, Ding Yihui, He Jinhai. The climate research of summer monsoon over the Western North Pacific[J]. Acta Meteorologica Sinica, 2005, 63(4): 418-430.
[26] 杨清华, 张林.西北太平洋表面风应力分布和周期特征分析[J]. 海洋预报, 2005, 22(4): 36-45. Yang Qinghua, Zhang Lin. Analysis of the distribution and period of the surface wind stress over the NW Pacific Ocean[J]. Marine Forecasts, 2005, 22(4): 36-45.
[27] Niiler P P, Maximenko N A, McWilliams J C. Dynamically balanced absolute sea level of the global ocean derived from near-surface velocity observations[J]. Geophys Res Lett, 2003, 30(22): 2164, doi: 10.1029/ 2003GL018628.
[28] Zhao Ning, Manda A, Han Zhen. Frontogenesis and frontolysis of the subpolar front in the surface mixed layer of the Japan Sea[J]. J Geophys Res: Oceans, 2014,119: 1498-1509, doi: 10.1002/2013JC009419.
[29] Dong Shenfu, Sprintall J, Gille S T, et al.. Southern Ocean mixed-layer depth from Argo float profiles[J]. J Geophys Res, 2008, 113, C06013. doi: 10.1029/ 2006JC004051.
(本文编辑: 刘珊珊)
Preliminary study on the frontogenesis and frontolysis of the oceanic temperature front in the northwest Pacific Ocean
ZHAO Ning1, HAN Zhen1, 2, LIU Xian-bo1
(1. Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education,Shanghai Ocean University, Shanghai 201306, China; 2. College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China)
Apr., 19, 2013
the northwest Pacific Ocean; ocean mixed layer; oceanic temperature front; frontolysis; frontogenesis
The mechanisms of the mixed layer temperature and temperature front in the northwest Pacific Ocean were investigated using climatology Argo, remote sensing wind, and reanalysis data from the National Center for Environmental Prediction/National Center for Atmospheric Research. Based on a mixed layer heat budget model,the net heat flux term was found to be the main controlling factor of temperature variability in the study region. Moreover, seasonal variations in the oceanic front were investigated and found to be strongest during September to February and weakest during May to August. This study determined that the strengthening and weakening of the temperature front were mainly controlled by the net heat fluxes and in particular, the net shortwave and net sensible heat fluxes.
P731.1
A
1000-3096(2016)01-0123-09
10.11759/hykx20130419002
2013-04-19;
2014-03-22
国家发改委卫星高技术产业化示范工程项目(2009214); 国家科技支撑计划(2013BAD13B00)
赵宁(1988-), 男, 江苏南京人, 硕士, 主要从事海洋遥感研究,E-mail: 343599711@qq.com; 韩震(1969-), 通信作者, 男, 教授, 博士,E-mail: zhhan@shou.edu.cn

