江西省教育支出效率空间分布特征分析

□文/李 颖（江西财经大学统计学院　江西·南昌）



江西省教育支出效率空间分布特征分析

□文/李 颖
（江西财经大学统计学院江西·南昌）

［提要］近年来，江西省的财政教育支出总量有了较大的增长，为教育事业的发展提供了有力保障。本文基于2013年江西省11个设区市教育投入和产出的相关统计数据，建立投入导向型的BCC模型，对教育支出效率进行评价，并利用Geoda软件对技术效率、纯技术效率、规模效率等进行空间分布特征分析。研究结果显示：江西省教育支出效率整体较好，其中南昌、鹰潭、新余以及赣州是DEA有效，处于规模报酬不变阶段；而其余地区非DEA有效，且处于规模报酬递增阶段；技术效率、纯技术效率、规模效率在空间分布上存在一定的相似性，且技术效率存在一定的空间负自相关性。

关键词：BCC模型；教育支出效率；空间分布特征

原标题：江西省教育支出效率的空间分布特征分析

收录日期：2016年3月22日

一、引言

近年来，江西省的经济得到了迅速发展，地区生产总值（GDP）从2005年的4，056.76亿元，增加到了2013年的14，338.5亿元，年均增长速度为17.3%。随着经济的不断发展，江西省对教育的投入总量也在逐渐增加。江西省财政教育支出由2005年的879，253万元增加到了2013年的6，645，302万元，占公共财政支出的比重由15.59%增加到了19.15%，占GDP的比重由2.17%增加到了4.63%。尽管财政教育支出总量逐年增加，但是需要在初等教育、中等教育及高等教育之间进行分配，必然会出现经费短缺的问题。由于资源具有稀缺性，有限的教育资源不能得到有效的利用，便会造成资源的浪费。如何解决教育经费不足与资源短缺的问题？一方面可以通过增加投入来解决教育经费不足的问题；另一方面可以提高教育资源的配置效率。然而，江西省处于经济欠发达的中部地区，增加教育经费投入的空间非常有限，因而提高教育支出效率显得尤为重要。

本文拟利用2013年江西省11个设区市教育的相关数据，建立DEA的BCC模型，分析教育支出效率，并尝试利用Geoda软件对其教育支出效率进行空间分布特征分析，这对优化江西省教育财政资源配置，提高财政教育支出效率具有重大意义。

二、实证分析

（一）研究方法。数据包络分析（简称DEA）是一种基于被评价对象间相对比较的非参数技术效率分析方法。DEA将效率测度的对象称为决策单元（DMU），其包含两个基本模型。第一个模型为CCR模型，假设规模报酬不变，其得出来的技术效率包含了规模效率成分。但是在现实生活中，并不是每一个DMU的生产过程都是处在规模报酬不变的状态下，鉴于此，Banker（1984）在CCR模型的基础上，提出了规模报酬可变的假设条件下的BCC模型，该模型将技术效率进一步分解为纯技术效率与规模效率，可衡量DMU在既定的生产技术情况下，是否处于最优生产规模状态。

（二）变量选取及数据来源。教育作为准公共产品，其投入包括人力投入、物力投入和财力投入，其产出包括直接产出和间接产出，而教育的直接产出主要是向社会培养学生，间接产出主要是教育对社会各个方面产生的作用。为此，结合数据的可获得性，本文选取小学、初中、高中和高等学校的专任教师数总和作为人力投入，小学、初中、高中和高等学校的学校数总和作为物力投入，财政教育支出作为财力投入；小学、初中、高中和高等学校所培养的在校学生数总和作为直接产出，人均GDP作为间接产出。本文所使用的数据均来源于《江西统计年鉴2014》，以及统计加工所得。

图1 技术效率的空间分布图

图2 纯技术效率的空间分布图

图3 规模效率的空间分布图

（三）分析结果解释。本文建立投入导向型的BCC模型，借助deap2.1软件，测算了2013年江西省11个设区市的教育支出的技术效率、纯技术效率、规模效率及规模报酬。整体上，江西省的技术效率、纯技术效率、规模效率分别为0.934，0.946，0.987，均小于1，非DEA有效。但是，3个效率值均在0.9以上，且规模效率接近于1，说明江西省教育支出效率较好。进一步，我们从江西省内部来评价纯技术效率、规模效率与技术效率。从纯技术效率来看，南昌、新余、鹰潭、赣州4个地区是纯技术有效的，其效率值为1，其他7个地区的纯技术效率均低于1，处于非有效状态。在处于非有效状态的地区中，其教育经费投入、学校投入、专任教师投入配置不合理，存在冗余较多的情况；从规模效率来看，除了南昌、鹰潭、新余、赣州4个地区是规模有效外，其余7个地区均处于非规模有效状态。在规模报酬分析中，除了南昌、鹰潭、新余、赣州4个地区是规模报酬不变外，其余7个地区均处于规模报酬递增阶段，说明这些地区教育需求还很大，教育事业任重道远。政府应该扩大这些地区的支出规模，加大投入，拉动产出的增加，促进教育事业快速发展；从技术效率来看，由于技术效率是纯技术效率与规模效率的乘积，因此各地区的技术效率与以上分析是相一致的。南昌、鹰潭、新余、赣州的技术效率为1，达到了DEA有效，即投入产出达到了最优状态，纯技术效率与规模效率都有效，而其他地区均处于非DEA有效状态。

三、空间分布特征分析

（一）三种效率的空间分布特征。根据江西省统计局的划分标准，江西省11个设区市可划分为赣北、赣中、赣南等三大地域，其中赣北地区包括南昌、景德镇、萍乡、九江、新余、鹰潭、宜春、上饶；赣中地区包括吉安和抚州；赣南地区包括赣州。为分析三种效率在空间上的分布特征，我们根据上文中三种效率的评价结果，利用Geoda软件绘制了三分位图，其结果如图1、图2、图3所示，其中颜色越深，代表效率值越高。（图1、图2、图3）

从图1、图2、图3中可以看出，南昌、鹰潭、新余、赣州颜色均最深，说明技术效率、纯技术效率、规模效率处于最优的水平；在图1、图2中，萍乡、九江、抚州的颜色最浅，说明这三个地区的技术效率与纯技术效率相对比较低；而景德镇、吉安、宜春、上饶的颜色处于两者之间，说明这些地区的技术效率与纯技术效率处于中等水平。在图3中，颜色最浅的地区与图2有所不同，减少了九江，增加了景德镇，说明九江的规模效率要好于其技术效率，而景德镇的规模效率却比其他地区低一些。

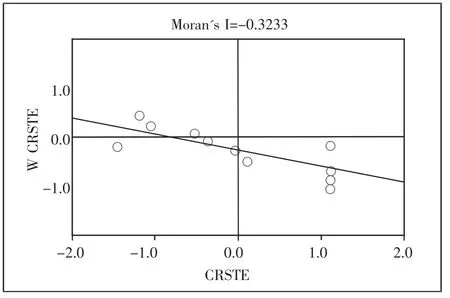
图4 技术效率的Moran’s I散点图

总体来说，技术效率、纯技术效率、规模效率的空间分布特征具有一定的相似性，赣州、南昌、鹰潭及新余，它们的技术效率、纯技术效率、规模效率均处于最优水平，而吉安、抚州以及赣北其他地区，它们的技术效率、纯技术效率、规模效率均没有达到最优水平，要不处于中等水平，要不处于较低水平，说明这些地区还有很大的发展空间，应努力达到最优水平。

（二）技术效率的Moran’s I指数分析。由于“地理学第一定律”的存在，在研究地区经济发展时，常常需要考虑空间自相关性。目前，在实际的空间自相关性研究中，测算和检验一个省份的经济行为是否存在集聚现象，通常的方法是计算Moran’s I指数。Moran’s I指数的取值范围为：大于0表示正相关，说明变量存在空间上的正相关性，值接近1时表示具有相似的变量聚集在一起（即高值与高值相邻、低值与低值相邻）；小于0表示负相关，值接近-1时表示具有相异的变量聚集在一起（即高值与低值相邻、低值与高值相邻），如果Moran’s I接近0，则表示变量是随机分布的，即不存在空间自相关性。（图4）

由于技术效率是纯技术效率与规模效率的乘积，既考虑了纯技术因素，又考虑了规模因素，是一种综合效率，因此我们运用Geoda软件，选择技术效率进行Moran’s I指数分析。从图4中可以看出，技术效率的Moran’s I为-0.3233，小于0，且利用蒙特卡洛模拟999次计算出其P值，发现未通过显著性水平为10%的检验，但通过了显著性水平为15%的检验，说明技术效率在空间分布上不存在显著的负自相关性，但是确实存在一定的负相关性，即技术效率高的地区与技术效率低的地区、技术效率低的地区与技术效率高的地区聚集在一起。

从图4中可以看出，位于第三象限的省份只有3个，只占总体的27.3%，而位于第二、第四象限的省份有8个，占总体的72.7%，可见，技术效率存在高—低和低—高的集聚特征。江西省应该利用技术效率高的地区带动技术效率低的地区，促进其发展，并赶超高水平地区，实现共同发展。

四、主要结论

本文利用2013年江西省11个设区市的教育投入和产出相关数据，建立BCC模型，测算出技术效率、纯技术效率及规模效率，并对三种效率进行空间分布特征分析。研究结果发现：从整体上来说，江西省教育支出效率非DEA有效，但从内部地区来说，有四个地区DEA有效，即南昌、赣州、鹰潭、新余，在非DEA有效的地区中，规模报酬呈现出递增状态；技术效率、纯技术效率具有相同的空间分布特征，而规模效率却有所不同，但呈现出与前两种效率相似的空间分布特征；技术效率在空间上存在一定的负自相关性，即技术效率高的地区与技术效率低的地区相邻。

主要参考文献：

［1］杨丽丽，朱卫东.地方政府教育支出效率及其影响因素分析［J］.教育财会研究，2014. 3.

［2］滕玉华，王火根.江西省教育支出效率的影响因素分析：基于11个设区市的面板数据［J］.无锡商业职业技术学院学报，2014.6.

［3］沙莎，刘鹏凌，栾敬东.基于DEA模型的我国区域教育效率评价研究［J］.安徽农业大学学报，2013.3.

［4］周凡磬，曹蓉.中国公共教育支出的效率现状及动态效率研究［J］.生产力研究，2013.9.

［5］康建英，张辉.基于DEA模型的义务教育经费支出效率评价［J］.衡水学院学报，2008.4.

［6］王世忠.民族地区义务教育财政支出状况评析———以广西壮族自治区为例［J］.中南民族大学学报，2013. 1.

中图分类号：F222

文献标识码：A