锯齿形单壁碳纳米管的穿透能研究

张　超, 潘成岭, 盛绍顶

(多尺度材料与分子催化实验室, 安徽理工大学材料科学与工程学院, 淮南 232001)



锯齿形单壁碳纳米管的穿透能研究

张超, 潘成岭, 盛绍顶

(多尺度材料与分子催化实验室, 安徽理工大学材料科学与工程学院, 淮南 232001)

摘要基于分子动力学方法, 研究了载能碳离子碰撞锯齿形单壁碳纳米管过程中初级碰撞原子(PKA)的运动过程和能量变化过程. 分析了手性指数为(2n+1,0)(n=2～9)的单壁碳纳米管中PKA的穿透能与载能碳离子入射能间的关系. 结果表明, 穿透能与入射能之间呈线性增长关系, 线性变化的斜率与碳纳米管直径有关. 通过分析PKA势能随模拟时间的变化规律, 阐述了初级碰撞原子的穿透能随入射能的增加而增加的物理机制.

关键词碳纳米管; 分子动力学; 能量转移; 穿透能; 碰撞

碳纳米管(CNT)[1]因独特的一维纳米结构, 在物理及化学等方面表现出了许多优异性能, 从而得到了广泛的研究[2～5]. 由于碳纳米管的性质强烈依赖于其结构, 所以对其结构进行调控和修饰是研究碳纳米管的一个重要方向[6,7].

采用荷能粒子束辐照碳纳米管是一种重要方法, 它能够以高度可控的方式改变材料的结构特性[8～10], 现已有许多研究通过粒子束辐照来改变碳纳米管的结构与性能[11～15]. Terrones等[16]利用电子束辐照800 ℃交叉叠放的单壁碳纳米管后, 观察到碳纳米管之间各种稳定的连接构型, 这些结构的产生主要是因为高温下电子束辐照产生的结构缺陷可以促进碳纳米管之间的连接; 他们进一步利用分子动力学模拟证实了空位和间隙原子能够诱导2个碳纳米管的连接. Gupta等[17]利用荷能粒子束对碳纳米管进行辐照后发现, 辐照时间延长可以明显增强单壁碳纳米管的导电性, 但对于多壁碳纳米管导电性的影响并不明显. Tolvanen等[18]通过低温扫描隧道显微镜并结合密度泛函理论方法, 研究了单壁碳纳米管受氩离子束辐照后电子结构的变化, 该结果对于以碳纳米管为基础的光电子器件具有潜在的应用价值. Zhao等[19]分别利用经验势分子动力学与第一性原理方法研究了低能离子辐照单壁碳纳米管过程中点缺陷的形成机制, 结果表明, 碰撞后入射离子与碳纳米管之间形成的化学键能够降低辐照阈值, 从而增强碳纳米管的辐照损伤. 这些结果对碳纳米管的材料改性, 以及对以碳纳米管为基础的电子器件的应用等方面具有重要的理论意义和应用价值. 本课题组[20～22]曾根据碳纳米管的结构特点, 在纳米管的表面分别选取不同的碰撞点, 采用分子动力学方法研究了碳纳米管中缺陷形成的入射阈能和几率分布情况. 通过对碰撞过程中原子结构的演化行为进行观察, 分析了典型缺陷的形成过程. 该研究对于了解碳纳米管中缺陷的形成机制, 操控碳纳米管中的缺陷使其向有利于工程应用方面的发展将有重要作用.

本文基于分子动力学方法(MD)研究了载能碳离子碰撞手性指数为(2n+1,0)(n=2～9)的单壁碳纳米管(CNT), 考察了初级碰撞原子(PKA)穿透碳纳米管后表面的运动规律、 穿透能与入射能间的关系, 穿透能与碳纳米管曲率半径间的关系, 并分析了该过程的物理机制.

1计算模型与方法

1.1初始结构

以手性指数为(2n+1,0)(n=2～9), 直径为0.39～1.49 nm, 原子数为120～456,z轴方向长度约为2.60 nm的锯齿形单壁碳纳米管为研究对象, 具体参数列于表1. 此外, 为了阐释当单壁碳纳米管手性指数为(2n,0)(n∈整数, 且n≥3)时, 高能离子碰撞后, 碳纳米管中PKA难以穿透碳纳米管后壁, 研究了能量为1 keV的载能碳离子轰击(8,0)单壁碳纳米管的动力学过程.

采用共轭梯度法对碳纳米管模型进行结构优化, 并在优化后的碳纳米管中间部分选择初级碰撞原子. 入射碳原子初始位置设置在PKA正上方且距离碳纳米管表面1.50 nm, 以避免初始阶段与碳纳米管发生相互作用.

1.2原子间势函数

(1)

(2)

(3)

式中: θi, θj, θk及rij, rjk, rik分别表示由i,j和k粒子组成的三角形的3个角和3条边.Z,p,h,b

和qn(n=1～5)分别为三体和两体部分参数. 这些参数均通过对碳团簇、 石墨及金刚石的键长、 键能、 弹性常数、 晶格结合能和晶格常数拟合得到, 具体参数见表2.

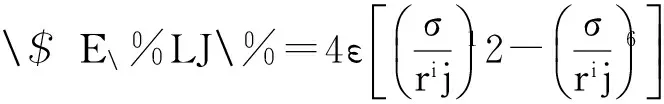
(4)

式中:ε为势阱深度, 表示2个原子间相互作用的强弱;σ表示两原子间作用势为0时原子间的距离. 对于碳原子体系,ε和σ分别取为2.86×10-3eV和0.24 nm.

1.3模拟细节

由于入射能量较低, 在碰撞过程中核阻止过程将占据主导地位, 所以电子阻止对碰撞过程的影响可忽略不计[10,13]. 为了与实验检测结果进行对比, 本文所指的入射碳原子统称为入射碳离子, 因为低电荷态对碰撞过程的影响可以忽略, 所以这种称谓是合理的[10,13]. 此外, 本文采用VMD[30]可视化软件观察原子结构的演化过程, 原子间成键距离设定为0.18 nm. 同时采用电荷自洽的密度泛函紧束缚方法[31]计算了碳纳米管的电荷密度, 以观察原子中电荷的空间分布.

2结果与讨论

2.1载能碳离子碰撞(8,0)单壁碳纳米管的动力学过程

图1给出了初始能量为1 keV载能碳离子轰击(8,0)单壁碳纳米管的动力学过程. 从图1可见, 随着演化进行, 入射离子逐渐靠近碳纳米管并碰撞PKA, 当模拟时间t=11 fs时, PKA受到入射离子的碰撞而离开原来位置. 随后, PKA逐渐靠近后壁, 并与后壁的次级碰撞原子(SKA)发生对心碰撞. 当t=15 fs时, SKA受到PKA的碰撞而离开了原来位置. 由t=10000 fs的最后演化构型图可以看出, 碳纳米管前壁由于少了一个原子, 最终演化成为5-1DB缺陷构型[32]; 碳纳米管后壁SKA位置被PKA所占据, 从而后壁变为完美的结构. 从图1还可见, 入射碳离子碰撞碳纳米管后自身受到斥力作用而反弹.

2.2载能碳离子碰撞(2n+1,0)(n=2～9)单壁碳纳米管的动力学过程

通过对(9,0)单壁碳纳米管的计算模拟发现, 当载能碳离子入射能20.0 eV≤Ein<40.0 eV时, 碰撞后PKA能够快速离开原来位置, 运行至碳纳米管后表面, 并与后表面原子发生非对心碰撞, 挤压后表面原子使其成为间隙原子, 而自身逐渐占据晶格格点位置, 这表明PKA从碰撞过程中获得的能量能够克服移位势垒而离开原来位置, 但不足以克服碳纳米管后表面的穿透势垒, 所以最终PKA停留在碳纳米管后表面. 碳纳米管前表面由于少了一个原子最终演化成为5-1DB缺陷构型[32].

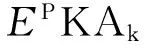
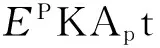
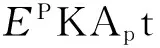
2.3PKA势能随模拟时间的变化关系及穿透能随入射能线性变化的机理

3结论

本文基于分子动力学方法, 研究了载能碳离子碰撞锯齿形单壁碳纳米管过程中PKA的运动行为. 结果发现, 载能碳离子碰撞(n,0)锯齿形单壁碳纳米管过程中, 当手性指数为(2n, 0)(n∈整数, 且n≥3)时, 碰撞后碳纳米管中PKA虽然能够离开原来的位置, 但难以穿透碳纳米管后壁, 即使采用初始能量比较高的载能碳离子轰击碳纳米管, PKA仍然难以穿透碳纳米管体系; 当手性指数为(2n+1, 0)(n∈整数, 且n≥2)时, 碰撞后碳纳米管中PKA不仅能够离开原来的位置, 而且能够相对容易地穿透碳纳米管后表面六元环而脱离体系. 研究了入射能为40.0～100.0 eV载能碳离子碰撞(2n+1, 0)(n=2～9)单壁碳纳米管过程中PKA的穿透能与载能碳离子入射能之间的关系. 结果发现, PKA穿透能随着入射能的增加而呈线性增长关系, 线性变化的斜率与碳纳米管的直径有关, 直径越大, 斜率越小. 通过对线性关系进行分析, 得到了消除热振动效应时的静态穿透能, 该能量随着碳纳米管直径的增加而增大, 最终趋于饱和值28.5 eV. 通过分析碰撞过程中PKA势能随模拟时间的变化规律, 发现PKA的势能随入射能的增加而增大, 从而解释了PKA的穿透能随着入射能的增加而增大的物理机制.

参考文献

[1]Iijima S.,Nature, 1991, 354, 56—58

[2]Perebeinos V., Tersoff J.,Phys.Rev.Lett., 2015, 114, 085501

[3]Niu L. L., Huang D., Du J. J., Wei Y., Hu C. F., Ye J. Y., Chen W. Y.,Chem.J.ChineseUniversities, 2015, 36(10), 1873—1879(牛璐璐, 黄棣, 杜晶晶, 魏延, 胡超凡, 叶家业, 陈维毅. 高等学校化学学报, 2015, 36(10), 1873—1879)

[4]Yang M. X., Ma J., Sun Y. R., Xiong X. Z., Li C. L., Li Q., Chen J. H.,Chem.J.ChineseUniversities, 2015, 35(3), 570—575(杨明轩, 马 杰, 孙怡然, 熊新竹, 李晨璐, 李强, 陈君红. 高等学校化学学报, 2015, 35(3), 570—575)

[5]Ma X. D., Roslyak O., Duque J. G., Pang X.Y., Doorn S. K., Piryatinski A., Dunlap D. H., Htoon H.,Phys.Rev.Lett., 2015, 115, 017401

[6]Ozden S., Autreto P. A. S., Tiwary C. S., Khatiwada S., Machado L., Galvao D. S., Vajtai R. V., Barrera E. V., Ajayan P. M.,NanoLett., 2014, 14(7), 4131—4137

[7]Aitkaliyeva A., Shao L.,Carbon, 2012, 50, 4680—4684

[8]Arenal R., Lopez-Bezanilla A.,ACSNano, 2014, 8(8), 8419—8425

[9]Aitkaliyeva A., Martin M. S., Harriman T. A., Hildebrand D. S., Lucca D. A., Wang J., Chen D., Shao L.,Phys.Rev.B, 2014, 89, 235437

[10]Krasheninnikov A.V., Nordlund K.,J.Appl.Phys., 2010, 107, 071301

[11]Titova L. V., Pint C. L., Zhang Q., Hauge R. H., Kono J., Hegmann F. A.,NanoLett., 2015, 15(5), 3267—3272

[12]Merrill A., Cress C. D., Rossi J. E., Cox N. D., Landi B. J.,Phys.Rev.B, 2015, 92, 075404

[13]Xu Z. J., Zhang W., Zhu Z. Y., Huai P.,Nanotechnology, 2009, 20, 125706

[14]Rossi J. E., Cress C. D., Merrill A., Soule K. J., Cox N. D., Landi B. J.,Carbon, 2015, 81, 488—496

[15]Yang J. Q., Li X. J., Ma G. L., Liu C. M., Zou M. N.,ActaPhys.Sin., 2015, 64, 136401(杨剑群, 李兴冀, 马国亮, 刘超铭, 邹梦楠. 物理学报, 2015, 64, 136401)

[16]Terrones M., Terrones H., Banhart F., Charlier J. C., Ajayan P. M.,Science, 2000, 288, 1226—1229

[17]Gupta S., Patel R. J., Smith N., Giedd R. E., Hui D.,DiamondRelat.Mater., 2007, 16, 236—242

[18]Tolvanen A., Buchs G., Ruffieux P., Gröning P., Gröning O., Krasheninnikov A. V.,Phys.Rev.B, 2009, 79, 125430

[19]Zhao S. J., Xue J. M., Wang Y. G., Yan S.,Appl.Phys.A, 2012, 108, 313—320

[20]Zhang C., Mao F., Dai J. X., Zhang F. S.,Comput.Mater.Sci., 2014, 93, 15—21

[21]Zhang C., Mao F., Zhang F. S., Zhang Y.,Chem.Phys.Lett., 2012, 541, 92—95

[22]Zhang C., Mao F., Zhang F. S.,Eur.Phys.J.Appl.Phys., 2013, 64, 10401

[23]Takai T., Lee C., Halicioglu T., Tiller W. A.,J.Phys.Chem., 1990, 94, 4480

[24]Tersoff J.,Phys.Rev.Lett., 1998, 61, 2879

[25]Brenner D. W.,Phys.Rev.B, 1990, 42, 9458

[26]Wang Z. X., Ke X. Z., Zhu Z. Y., Zhang F. S., Ruan M. L., Yang J. Q.,Phys.Rev.B, 2000, 61, R2472

[27]Mao F., Zhang C., Zhang Y., Zhang F. S.,Chin.Phys.Lett., 2012, 29(7), 076101

[28]Jones J. E.,Proc.R.Soc.Lond.A, 1924, 106(738), 463—477

[29]Swope W. C., Andersen H. C., Berens P. H. , Wilson K. R.,J.Chem.Phys., 1982, 76, 637—649

[30]Humphrey W., Dalke A., Schulten K.,J.Mol.Graphics, 1996, 14, 33—38

[31]Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., Seifert G.,Phys.Rev.B, 1998, 58, 7260—7268

[32]Lu A. J., Pan B. C.,Phys.Rev.Lett., 2004, 92, 105504

(Ed.: Y, Z, S)

† Supported by the National Natural Science Foundation of China(Nos.11505003, 21201006), the Natural Science Foundation of Anhui Province, China(No.1608085QA20) and the Introduced Doctor’s Startup Fund from the Anhui University of Science and Technology, China(No.ZX944).

Study on the Penetrating Energy of Zigzag Single-walled Carbon Nanotubes†

ZHANG Chao, PAN Chengling*, SHENG Shaoding

(LaboratoryofMultiscaleMaterialsandMolecularCatalysis,SchoolofMaterialsScienceandEngineering,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

KeywordsCarbon nanotube; Molecular dynamics; Energy transfer; Penetrating energy; Collision

AbstractThe movement process and energy change of the primary knock-on atom were investigated after an energetic carbon ion colliding with single-walled carbon nanotubesviaa molecular dynamics method. The relationship between the penetrating energy of the primary knock-on atom and the incident energy of the projectile carbon ion was analyzed for (2n+1,0)(n=2—9) zigzag single-walled carbon nanotubes. It was found that the penetrating energy increases linearly with the incident energy in the energy range under discussion. The linear slop was related to the nanotube diameter. The physical mechanism of linear increase was explained in detail by analyzing the time evolution of the potential energy of primary knock-on atom.

收稿日期:2016-02-17. 网络出版日期: 2016-05-26.

基金项目：国家自然科学基金(批准号: 11505003, 21201006)、 安徽省自然科学基金(批准号: 1608085QA20)和安徽理工大学科研启动基金(批准号: ZX944)资助.

中图分类号O644.2; O613.7

文献标志码A

联系人简介: 潘成岭, 男, 博士, 教授, 主要从事多尺度材料的性能研究. E-mail: chengling_pan@126.com