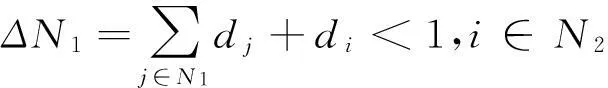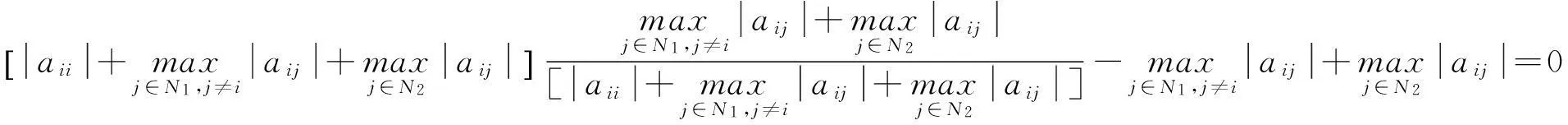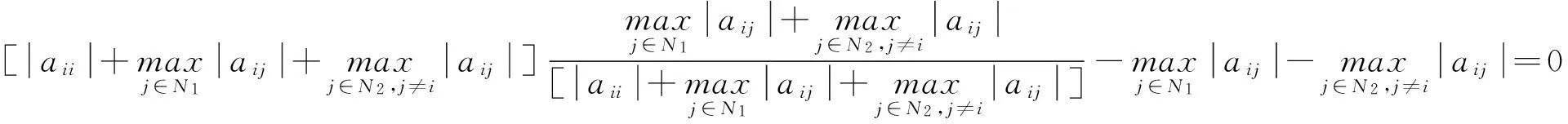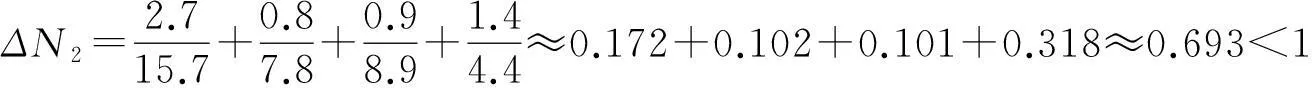H-矩阵一组新的实用判定法

邰志艳，吴　希，牛新宇

(吉林医药学院数学教研室，吉林 吉林 132013)

H-矩阵一组新的实用判定法

邰志艳，吴希，牛新宇

(吉林医药学院数学教研室，吉林 吉林 132013)

[摘要]根据严格对角占优矩阵理论，运用不等式放缩技巧，给出了非奇异H-矩阵的几个新的判定定理，改进了近期已有的判定方法，并用实际算例说明了这些判定方法的有效性及优越性.

[关键词]H-矩阵；对角占优矩阵；正对角矩阵

1预备知识

非奇异h-矩阵是一类具有很强理论研究价值和重要实际应用背景的特殊矩阵类，它在神经网络大系统稳定性、线性时滞系统稳定性的研究中有着重要的应用，但对其进行实际判别却很困难.[1-9]本文给出了非奇异h-矩阵的几个新的判定定理，改进了文献[1]的主要结果，给出了新的判定条件.

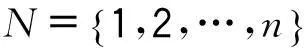
若存在N1，N2⊂N满足N1∩N2=φ，且N1∪N2=N，则称N1和N2为集合N的划分，记做N=N1⨁N2.

这里约定，当N=N1⨁N2时，N1≠∅，N2≠∅，且为了书写方便把Λi(A)简记为Λi.

2主要结果与证明

(1)

则A是非奇异h-矩阵.

综上，∀i∈N，

(2)

从而

B=AX∈D，

(3)

即A是非奇异h-矩阵.

注易见当n>2时，定理1改进了文献[1]中的部分结果.

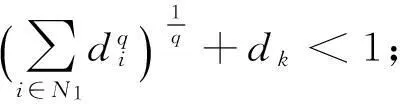
其中

则A是非奇异h-矩阵.

证明由已知条件知，∀i∈N，有0

(ⅰ)∀i∈N1，由hölder不等式有

(ⅱ)∀i∈N2，由hölder不等式有

综上可知，∀i∈N，有(2)式成立，进而(3)式成立，故A是非奇异h-矩阵.

其中

则A是非奇异h-矩阵.

(ⅰ)∀i∈N1，有

(ⅱ)∀i∈N2，有

综上可知，∀i∈N，有(2)式成立，进而得(3)式成立，故A是非奇异h-矩阵.

3数值算例

例1设

由定理2知A为非奇异h-矩阵.

而用文献[1]中定理2结果计算得

此时无法判别A是否为非奇异h-矩阵.

[参考文献]

[1]侯进军，李斌.H-矩阵的一组新判定[J].应用数学学报，2008，31(2):266-270.

[2]徐仲，路全.判定广义对角占优矩阵的一组充分条件[J].工程数学学报，2001，18(3)：11-15.

[3]孙玉祥.广义对角占优矩阵的充分条件[J].高等学校计算数学学报，1997，19(3)：216-223.

[4]苗晨.Ostrowski对角占优矩阵与非奇异H-矩阵的一个判别定理[J].东北师大学报(自然科学版)，2014，46(1)：157-160.

[5]邰志艳，李庆春.局部双对角占优矩阵及其应用[J].吉林大学学报(理学版)，2013，51(2):207-211.

[6]谢清明.关于H-矩阵的实用判定的注记[J].应用数学学报，2006(6):1080-1084.

[7]VARGA R S.On recurring theorems on diagonal dominace[J].Linear Algebra Appl，1976，13:1-9.

[8]邰志艳，李庆春，胡硕.α-对角占优矩阵的等价表征及应用[J].吉林大学学报(理学版)，2015，53(5):934-938.

[9]刘钰靖.严格α-链对角占优矩阵的等价表征及应用[J].东北师大学报(自然科学版)，2013，45(1)： 17-20.

(责任编辑：李亚军)

A set of new criteria for H-matrices

TAI Zhi-yan，WU Xi，NIU Xin-yu

(Department of Mathematics，Jilin Medical University，Jilin 132013，China)

Abstract:Based on the theory of strictly diagonally dominant matrices，using some techniques for inequalities，several new sufficient conditions to determine non-singular H-matrices are given and thus the corresponding results are improved and generalized.These conditions have improved some relate existed results for non-singular H-matrices.The validity and superiority of the results are verified by a numerical example.

Keywords:H-matrices；diagonally dominant matrices；positive diagonally matrices

[文章编号]1000-1832(2016)02-0048-04

[收稿日期]2015-10-06

[基金项目]国家自然科学基金资助项目(11171133)；吉林省教育厅科学技术研究项目(2015393).

[作者简介]邰志艳(1976—)，女，硕士，副教授，主要从事矩阵代数理论研究.

[中图分类号]O 151.21[学科代码]110·2110

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.012