Pytkeev空间与弱FU空间的几个注记

王汉锋，贺　伟

(1.山东农业大学数学系，山东 泰安 271018;2.南京师范大学数学科学学院，江苏 南京 210023)

Pytkeev空间与弱FU空间的几个注记

王汉锋1，贺伟2

(1.山东农业大学数学系，山东 泰安 271018;2.南京师范大学数学科学学院，江苏 南京 210023)

[摘要]讨论了Pytkeev空间与弱FU空间几个映射的性质，得到了两类空间被连续映射保持与逆保持的几个结论，纠正了Malykhin与Tironi的两个错误证明.

[关键词]Pytkeev空间；弱FU空间；闭映射；完全映射；可数紧度

1预备知识

弱第一可数空间是一类重要的拓扑空间，它们的出现丰富了拓扑空间中点的逼近与邻近理论，因而成为一些拓扑学家研究的热门领域.比较典型的弱第一可数空间有Fréchet空间、序列空间、子序列空间等，[1-3]近些年来许多更弱的相对序列空间被引入，如α-序列空间、β-序列空间、filter-Fréchet空间等.[4-5]弱第一可数空间对于一些拓扑公开问题的解决起到了重要作用，如在著名的Mi-空间方面(i=1，2，3)，Mizaokami与Shimane先是证明了Fréchet空间+M3-空间是M1-空间，后又证明了k-空间+M3-空间是M1-空间.[6-7]

本文所讨论的弱FU空间与Pytkeev空间是由Malykhin[8]引入的两类空间，它们界于Fréchet空间与具有可数紧度的空间之间，其中弱FU空间是Fréchet空间的直接推广，它把Fréchet空间中收敛序列中的点列弱化为互不相交有限集列，得到了一个比序列空间还弱的空间；而Pytkeev空间则将可数紧度性质中可数的点列变为由无限集组成的集列，得到了一个比可数紧度空间更强的空间.这两类空间对于进一步研究弱第一可数空间的结构关系，探索不同空间之间的联系有着重要的意义.

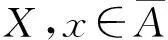
定义5[1]设x，y为拓扑空间，我们给出下面定义：

(1)称f:x→y为闭映射，是指对x的每个闭集f，f(f)是y的闭集；

(2)称f:x→y为完全映射，是指f是闭映射，且对每个y∈y，f-1(y)是紧集；

(3)称f:x→y为伪开映射，是指对每个y∈y，f-1(y)⊂u∈τ(x)，都有y∈f0(u)，其中f0(u)表示f(u)在y中的内部;

(4)称f:x→y为有限(可数)到一的，是指对每个y∈y，f-1(y)是有限(可数)的.

定义6[10]设x为拓扑空间，x∈x，Γ={Oα|α∈Λ}是由x的开集构成的集合，Υ={Pβ|β∈Δ}是x的一个集族.若对x的每个邻域u，都有Oα∈Γ使得Oα⊂u，则称Γ={Oα|α∈Λ}是x的π-邻域基；若对x的每个邻域u，都有Pβ∈Υ使得Pβ⊂u，则称Υ={Pβ|β∈Δ}是x的π-网.

2主要结论

定理1若f:x→y是闭映射，x是Pytkeev空间，则y是Pytkeev空间.

例1存在一个Pytkeev空间x及开映射f:x→y，但y不是Pytkeev空间.

证明设x={0}∪{(n，k)|k，n∈N}，βN是N的Stone-Cěch紧化[9]，p∈βNN，即p为N上的一个极大滤子，以NN表示从N到N内的全体函数构成的集合.令v(n，m)={(n，k)|k≥m}，对f⊂N，f∈NN，记h(f，f)=∪{v(n，f(n))|n∈f}.

下面证明x是Pytkeev空间.

因为在x中只有点x=0是非孤立点，所以只对x=0进行讨论.

设y=N∪{p}，p为上述极大滤子，y作为βN的子空间，具有子空间拓扑，即N中的点为孤立点，点p的邻域为形如{p}∪f的子集，其中f∈p.

下面用反证法证明y不是Pytkeev空间.

映射f:x→y定义如下：f(0)=p，对每个n∈N，f({(n，k)|k∈N})={n}，容易验证f是连续映射，下面证明f是开映射，从而Pytkeev空间性质不被连续开映射所保持.

设u∈τ(x)，若0∉u，则f(u)⊂N，由于N是y的离散开子空间，所以f(u)∈τ(y)；若0∈u，则存在f={ni|i∈N}∈p及f∈NN使得{0}∪h(f，f)⊂u，所以{0}∪f⊂f(u)，故f(u)∈τ(y)，因此f是开映射.

由于例1中的f是可数到一的，故可数到一的开映射不一定保持Pytkeev空间性质.

定理2若f:x→y是有限到一的伪开映射，x是Pytkeev空间，则y是Pytkeev空间.

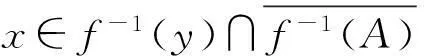
推论1若f:x→y是有限到一的开映射，x是Pytkeev空间，则y是Pytkeev空间.

定理3若f:x→y是闭映射，x是弱FU空间，则y是弱FU空间.

下面的定理4与定理5给出改正后的证明.由于文献[8]指出了紧的可数紧度空间是Pytkeev空间，Pytkeev空间是弱FU空间，故可将文献[8]中的可数紧度纤维条件改为Pytkeev纤维或弱FU纤维.

定理4设f:x→y是完全映射，y是Pytkeev空间.若对每个y∈y，f-1(y)是Pytkeev空间，则x是Pytkeev空间.

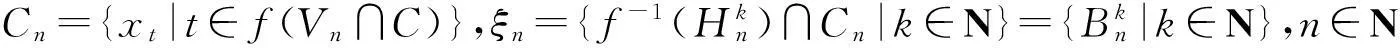
下面证明x(π)ξ.

由上述(1)、(2)知，x是Pytkeev空间.

由于下面定理5的前半部分证明与定理4完全类似，因此只证明后半部分.

定理5设f:x→y是完全映射，y是弱FU空间.若对每个y∈y，f-1(y)是弱FU空间，则x是弱FU空间.

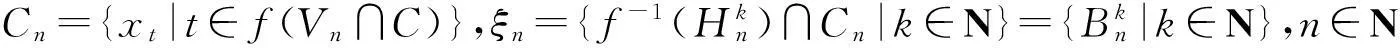
为了证明x是弱FU空间，需要证明{ξn|n∈N}满足如下两个引理.

综上，x是弱FU空间.

[参考文献]

[1]林寿.广义度量空间与映射[M].北京：科学出版社，1995：51-79.

[2]高国士.拓扑空间论[M].北京：科学出版社，2000：42-47.

[3]FRANKLIN S P，RAJAGOPALAN M.On subsequential spaces [J].Topology and its Applications，1990，35：1-19.

[4]ARHANGEL’SKII A V，NOGURA T.Relative sequentiality [J].Topology and its Applications，1998，82：49-58.

[5]ARHANGEL’SKII A V.Relative topological properties and relative topological spaces [J].Topology and its Applications，1996，70：1-13.

[6]CEDER J G.Some generalizations of metric spaces [J].Pacific J Math，1961，11：105-125.

[7]MIZAOKAMI T，SHIMANE N.On the M3versus M1problem [J].Topology and its Application，2000，105：1-13.

[8]MALYKHIN V I，TIRONI G.Weakly Frechet-Urysohn and Pytkeev spaces [J].Topology and its Applications，2000，104：181-190.

[9]儿玉之宏，永见启用.拓扑空间论[M].北京：科学出版社，2001:292-303.

[10]李琦.等边η-形式正则性的新证明[J].东北师大学报(自然科学版)，2014，46(2)：22-24.

(责任编辑：李亚军)

Several notes on Pytkeev spaces and weakly FU spaces

WANG Han-feng1，HE Wei2

(1.Department of Mathematics，Shandong Agricultural University，Taian 271018，China;2.College of Mathematics，Nanjing Normal University，Nanjing 210023，China)

Abstract:Several mapping properties about Pytkeev spaces and weakly FU spaces are investigated and some results on being preserved and adversely preserved about the two class of spaces are given by continuous mappings.Moreover，two wrong proofs by Malykhin and Tironi are corrected.

Keywords:Pytkeev spaces；weakly FU spaces；closed mapping；perfect mapping；countable tightness

[文章编号]1000-1832(2016)02-0044-04

[收稿日期]2014-12-28

[基金项目]国家自然科学基金资助项目(11171156)；山东省自然科学基金资助项目(ZR2014AL002).

[作者简介]王汉锋，男，博士，讲师，主要从事拓扑学研究.

[中图分类号]O 189.1[学科代码]110·31

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.011