几类特殊曲线的微分几何理论研究

孙建国，裴东河

(1.中国石油大学理学院，山东 青岛 266580；2.东北师范大学数学与统计学院，吉林 长春 130024)

几类特殊曲线的微分几何理论研究

孙建国1，裴东河2

(1.中国石油大学理学院，山东 青岛 266580；2.东北师范大学数学与统计学院，吉林 长春 130024)

[摘要]伪零曲线与偏零曲线在物理学研究中起着非常重要的作用.通过伪向量积与Frenet方程，可得伪零曲线与偏零曲线的微分几何性质；局部上，通过曲率等几何量可以描述子流形与伪球的切触；同时给出伪零曲线与偏零曲线的AW(k)型存在条件.

[关键词]AW(k)型曲线；偏零曲线；伪零曲线；刘维尔联络

1915年，爱因斯坦发现广义相对论实际上就是在伪欧氏空间中空间、时间和引力的形成理论，在此之后，很多科学家对伪欧氏空间进行了系统的研究.[1-10]伪欧氏空间与欧氏空间的主要不同点就是光向量的出现，因此伪欧氏空间中的子流形的几何性质与欧氏空间中子流形的几何性质有很大的区别.[3-4，9-10]当三维欧氏空间增加一个类时向量时，该空间就成了四维Minkowski空间，同时Minkowski几何对广义相对论经典理论的应用起到非常大的作用.在Minkowski空间中，光线可以看成为零向量所在的直线，因此对带有零向量标架的曲线进行研究具有一定的物理学意义.本文主要讨论在四维Minkowski空间中由类空向量所拓展的伪零曲线与偏零曲线的几何意义.

Arslan和West在1995年给出了子流形的AW(k)型概念的应用，同时Arslan等讨论了欧氏空间和Minkowski空间中部分子流形的AW(k)型性质.[1，3-4，6-9]然而，到目前为止人们对Minkowski空间曲线AW(k)型性质的研究都是在非类光Frenet标架下进行的，本文主要对Minkowski空间中带有类光标架下的类空曲线的伪零曲线与偏零曲线的AW(k)型曲线几何性质进行研究.

若无特殊说明，本文所有曲线或曲面都为光滑的.

1预备知识

设R4={(x1，x2，x3，x4)|xi∈R(i=1，2，3，4)}为四维向量空间.对于任意两个向量x=(x1，x2，x3，x4)与y=(y1，y2，y3，y4)，定义x与y的伪向量积为：

〈x，y〉=x1y1+x2y2+x3y3-x4y4，

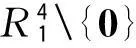
2偏零曲线的几何性质

(1)

γ′(s)=T(s)；

记：

N1(s)=k1(s)N(s)；

(2)

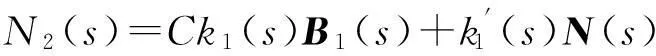
(3)

(4)

注2.1γ′(s)，γ″(s)，γ‴(s)和γ″″(s)为线性无关的，当且仅当向量N1(s)，N2(s)和N3(s)是线性无关的.

定义2.1对于一类空曲线，有如下分类：

(ⅰ)若曲线满足N3(s)=0，则称该曲线为AW(1)型曲线；

(ⅱ)若曲线满足

‖N2(s)‖2N3(s)=〈N3(s)，N2(s)〉N2(s)，

(5)

则称该曲线为AW(2)型曲线；

(ⅲ)若曲线满足

‖N1(s)‖2N3(s)=〈N3(s)，N1(s)〉N1(s)，

(6)

则称该曲线为AW(3)型曲线.

定理2.1设γ(s)为密切数为3的偏零曲线，则γ(s)为AW(1)型曲线，当且仅当

k1(s)=0.

(7)

定理2.2设γ(s)为密切数为3的偏零曲线，则γ(s)为AW(2)型曲线，当且仅当

(8)

证明设γ(s)为AW(2)型偏零曲线，将(3)—(4)式代入到方程(5)中得

因此可得方程(8).反之亦然.

定理2.3设γ(s)为密切数为3的偏零曲线，则γ(s)为AW(3)型曲线，当且仅当

k1(s)=C，

(9)

其中C为常数.

证明设γ(s)为AW(3)型偏零曲线，故该曲线满足方程(6)，将(2)与(4)式代入到方程(6)中得

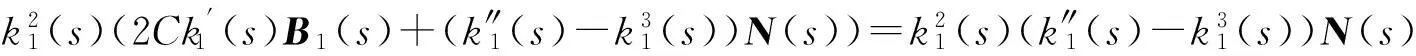
推论2.1设γ(s)为密切数为3的偏零曲线，且γ(s)为AW(1)型曲线.则γ(s)也为AW(i)(i=2，3)型曲线.

3伪零曲线的几何性质

(10)

γ′(s)=T(s)；

记：

N1(s)=N(s)；

(11)

N2(s)=k1(s)B1(s)；

(12)

(13)

注3.1γ′(s)，γ″(s)，γ‴(s)和γ″″(s)为线性无关的，当且仅当向量N1(s)，N2(s)和N3(s)是线性无关的.

定理3.1设γ(s)为密切数为3的伪零曲线，则γ(s)为AW(1)型曲线，当且仅当

k1(s)=0.

(14)

证明设γ(s)为AW(1)型伪零曲线，由方程(13)直接可得方程(14).反之显然成立.

定理3.2设γ(s)为密切数为3的伪零曲线，则γ(s)为AW(2)型曲线，当且仅当

k1(s)=0.

(15)

证明设γ(s)为AW(2)型伪零曲线，则在曲线γ(s)上方程(5)成立，将(12)—(13)式代入到方程(5)中，可得k1(s)=0.反之显然成立.

定理3.3设γ(s)为密切数为3的伪零曲线，则γ(s)为AW(3)型曲线，当且仅当k1(s)=0.

证明设γ(s)为AW(3)型伪零曲线，将(1)，(13)式代入方程(6)可知该定理正确.反之亦然.

推论3.1设γ(s)为密切数为3的伪零曲线，γ(s)为AW(i)(i=1，2)型曲线.则γ(s)定为AW(j)(i≠j，i=1，2，3)型曲线.

[参考文献]

[1]ARSLAN K，ÖZGÜ C.Curves and surfaces of AW(k)-type[M].Singapore：World Scientific，1999：21-26.

[2]DUFFAL K L，JIN D H.Null curves and hypersurfaces of semi-riemannian manifolds[M].Singapore：World Scientific，2007：87-103.

[3]KÜLAHCI M，ERGÜT M.Bertrand curves of AW(k)-type in Lorenzian space[J].Nonlinear Anal，2009，70：1725-1731.

[5]刘海明，孙伟志，苗佳晶.关于函数芽的相对通用形变和通用开折[J].东北师大学报(自然科学版)，2009，41(2):30-34.

[6]O’NEILL B.Semi-riemannian geometry with applications to relativity[M].London：Academic Press，1983：21-83.

[7]ÖZGÜR C，GEZGIN F.On some curves of AW(k)-type[J].Diff Geom Dyn Syst，2005(7):74-80.

[8]SUN J G，PEI D H.Null surfaces of null curves on 3-null cone[J].Phys Lett A，2014，378:1010-1016.

[9]SUN J G，PEI D H.Some new properties of null curves on 3-null cone and unit semi-Euclidean 3-spheres[J].J Nonlinear Sci Appl，2015(8):275-284.

[10]WAKRAVE J.Curves and surfaces in Minkowski space[M].Leuven：KU Leuven，1995：232-304.

(责任编辑：李亚军)

Differential geometry properties of some special curves

SUN Jian-guo1，PEI Dong-he2

(1.School of Science，China University of Petroleum，Qingdao 266580，China；

2.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China)

Abstract:Pseudo null curves and partially null curves have important physical meanings.Via the pseudo-scalar product and Frenet equations，the differential geometry of pseudo null curves and partially null curves is obtained.In local sense，the curvature and other geometric quantity can describe the contact of submanifolds with pseudo-spheres.On the other hand，the existence conditions of pseudo null curve and partially null curves are given.

Keywords:AW(k)curve；partially null curve；pseudo null curve；Levi-Civita connection

[文章编号]1000-1832(2016)02-0040-04

[收稿日期]2015-03-20

[基金项目]国家自然科学基金资助项目(11271063)；山东省自然科学基金(青年)资助项目(ZR2014AQ016)；中央高校创新基金资助项目(15CX02068A).

[作者简介]孙建国(1981—)，男，博士，讲师，主要从事微分几何与奇点理论研究.

[中图分类号]O 189.1[学科代码]110·3155

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.010