基于伪单输入多输出系统的子波提取研究❋

张汉羽， 刘怀山， 邢　磊❋❋, 石旭亮，雷朝阳

(1.中国海洋大学海底科学与探测技术教育部重点实验室， 山东 青岛 266100； 2.中国科学院深海科学分工程研究所， 海南 三亚 572000)



基于伪单输入多输出系统的子波提取研究❋

张汉羽1，2， 刘怀山1， 邢磊1❋❋, 石旭亮1，雷朝阳1

(1.中国海洋大学海底科学与探测技术教育部重点实验室， 山东 青岛 266100； 2.中国科学院深海科学分工程研究所， 海南 三亚 572000)

摘要：单输入多输出系统提取地震子波的方法存在要求地震道之间的反射系数相同，子波多个且相异(即假设地震记录的差异全部由子波造成，与反射系数无关)，以及对噪声敏感等缺陷。为了克服这种假设，本文利用地震数据的频率特征，运用二进正交小波变换Mallat算法的思想，讨论了两种构建伪单输入多输出系统的方法，推导了该系统下噪声子空间提取地震子波的算法,并进行了模型测试和实际资料验证工作。测试和验证结果显示该方法具有较强的抗噪能力。

关键词：PSIMO系统； 子空间； Mallat算法； 子波提取

引用格式：张汉羽，刘怀山，邢磊，等.基于伪单输入多输出系统的子波提取研究[J]. 中国海洋大学学报(自然科学版)， 2016,46(6): 74-83.

ZHANG Han-Yu, LIU Huai-Shan, XING Lei, et al. Based on the pseudo single-input multi-output system to extract seismic wavelet[J]. Periodical of Ocean University of China, 2016, 46(6): 74-83.

能否准确地估计地震子波是地震资料波阻抗反演、反褶积处理及正演模拟成败的关键因素之一[1]。目前子波提取方法主要有统计性方法和确定性方法[2]。统计性方法是指在地震子波和反射系数都未知的情况下，根据地震记录来估计子波[2]，其不需要借助测井资料，但一般需要假设地层反射系数是高斯分布的随机序列，子波相位是最小相位、零相位和最大相位，而实际的子波一般为混合相位[1]，或者需要运用高阶统计量的理论，假设反射系数是非高斯随机序列，也要求较多的资料才能获得较好的估计结果[2]，包括分形法[4-5]、倒双谱法[3]、高阶统计量FIR系统辨识[6-7]、同态法[8-10]、相位估计法[11-14]、全通子波匹配法[15]、EYW方程法[16-17]等。确定性方法则是通过测井资料结合井旁地震记录来求取子波，包括贝叶斯法[18]、循环迭代法[19]、线性反演方法等。

基于单输入多输出系统(Single-Input Multi-Output System，简称SIMO)的二阶统计量盲信道辨识方法广泛应用到通讯技术等领域[20-21]。杨培杰等[2，22]将子波提取纳入盲信号处理领域，提出了SIMO系统混合相位子波提取的算法，其不需要对反射系数分布规律和子波相位进行假设，又具有准确度高、计算量小且速度快等优点，为二阶统计量的子波提取开拓了新思路。但这种方法隐含地假设了地震道之间的反射系数相同，子波多个且相异，即地震记录的差异全部由子波造成，与反射系数无关，且对噪声敏感[22]。当只有一个地震道时，也不能照搬通讯领域的过采样技术将单输入单输出系统(Single-Input Single-Output System, 简称SISO)转化为SIMO系统，这使其难以在实际地震资料中应用。

为了继承SIMO系统估计子波方法，对子波相位和反射系数分布规律无假设的优点，避免地震道之间反射系数相同，地震道之间的差异全部由子波造成的不合理假设，笔者从褶积模型出发，利用地震数据的频率特征，运用二进正交小波变换Mallat算法的思想，讨论了两种构建伪单输入多输出系统(Pseudo Single-Input Multi-Output System,简称PSIMO)的方法，推导了PSIMO系统下噪声子空间法提取子波的算法，也测试了它的抗噪能力，还应用到实际地震资料处理中，估计出实际地震子波，并将估计子波视为已知子波，对整个剖面进行反褶积处理。反褶积处理剖面显示，同相轴变得更加精细、连续和平整，效果明显。

1PSIMO系统的构建

时间域地震记录可表示为

s=w*r+v 。

(1)

式中：*为褶积运算；s为地震记录；w为地震子波；r为地层反射系数；v为加性高斯噪声。将(1)式展开并离散：

(2)

式中：n为采样点；L+1为子波点数；T为采样间隔；J为总采样点数，则离散化地震记录的每个采样点对应的时间为t=nT。若将w视为系统函数，r视为激励函数，s视为系统激励响应，则(2)式可视为一个SISO系统[21-22](见图1)。

1.1 小波变换Mallat思想构建PSIMO系统

A*Lo_D*Lo_R+A*Hi_D*Hi_R=A*δ=A 。

(3)

式中：A为任意层信号； Lo_D为低频分解小波函数；Hi_D为高频分解小波函数；Lo_R为低频重构小波函数；Hi_R为高频重构小波函数；δ为单位脉冲函数。(3)舍去抽取与插值环节的分解重构过程，其本质是多次褶积运算，而褶积运算满足交换律，多次褶积过程可以不分先后，故对地震记录的分解重构等价于构造地震子波，不影响地层反射系数(见公式(4)～(5))。

按照Mallat算法[29]二叉树的分解重构形式，将一个地震道s(SISO系统，见图1)构造成PSIMO(见图2)系统的具体过程如下：

(1)进行p次分解

第一次分解

u1high=s*Hi_D，

第二次分解

u2high=s*Hi_D，

……。

第p次分解

(2)将每一层分解信号重构

第一层重构

第二层重构

……。

第p层低、高频重构

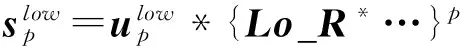
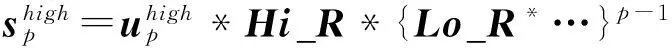
按小组进行分组训练，小组同学相互交流，并对各小组学生的任务实施过程进行全程跟踪指导，并对其出现的问题进行总结和评价，指出各组学生在程序编码过程中存在的某些共性问题。例如，程序源文件命名不规范、程序编写格式不规范、死循环、无注释或注释不清晰等问题。

综合上述分解和重构过程和公式(1)，进行p次分解时，任意层n(≤p)信号重构表达式为

(4)

设需要构造一个单输入P输出的PSIMO系统(见图2)，则需获得P个虚拟地震子道，这里称伪子道。按照Mallat二叉树形式，须进行P-1次分解重构，重构的第i个伪子道xi可简单表示为：

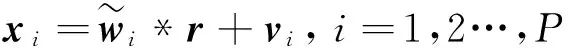
(5)

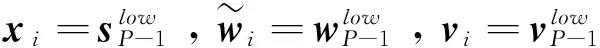
(a.db4基小波等价算子时域和频域曲线 Time domain and frequency domain curves of db4 base wavelet equivalent operator； b.中间截断等价算子时域和频域曲线 Time domain and frequency domain curves of middle truncation equivalent operator)

图3等价算子分析

Fig.3Analysis of equivalent operator

(6)

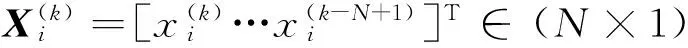
rk=[r(k),…,r(k-N-L-q+1)]T∈(N+L+q)×1，

(7)

1.2 高信噪比小波层位构建PSIMO系统

在1.1的基础上，从信噪比的角度考虑：(1)地震信号和噪声在小波层位上分布差异较大，如图4所示，在主频40Hz，延续时间2s的地震记录上，加入高斯噪声，使初始信噪比分别为50、30、20、10、0db(见图例)，选用db1和db4基小波进行7次分解，重构每一层位的信号，并求得重构信号的信噪比分布情况。从图4a、b上可以看到，不同层位上的信号和噪声相差较大，层位越低，信噪比越高，故可选择高信噪比层位重构信号；(2)SIMO系统盲辨识算法要求系统函数之间互素[25]，故在构建PSIMO系统时，也须考虑构造子波(系统函数)的差异性。由于考虑到基小波种类多样且互素，滤波强度也不一，如图4a和b所示，db1基小波4～8层位的信噪比比原来高出2～10db，db4基小波7～8层位的信噪比比原来高出6～7db，故可选取不一样的基小波分解信号，并只重构回高信噪比层位构建PSIMO系统，这样既能保证构造子波的差异性，又能提高PSIMO系统的信噪比。

这种构造的具体推导与上文1.1相似，最终得到的表达式与(6)～(7)一样，仅仅选用了多种基小波函数，此时等价算子可表示为

(8)

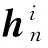
2地震子波提取

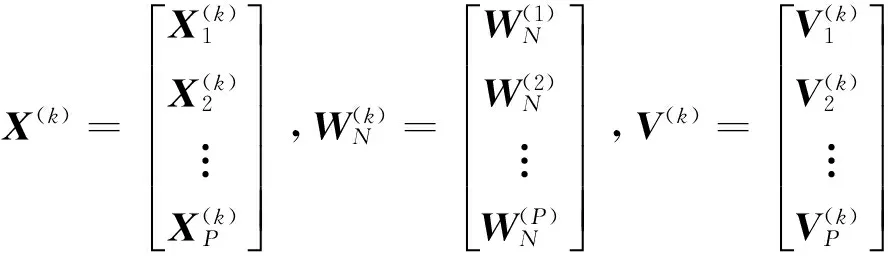
(9)

则(7)式可以写成

(10)

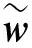
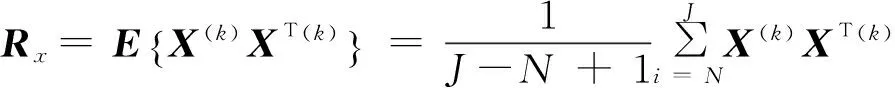
(11)

则(10)式可写成

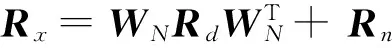
(12)

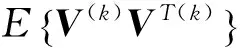
(13)

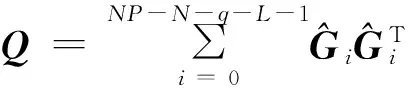
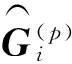
(14)

将方法一(1.1构造方法)和方法二(1.2构造方法)估计的伪子波，转化估计子波的表达式为

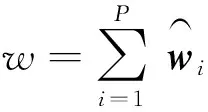
(15)

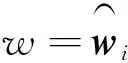
(16)

3模型验证

采用混合高斯模型，生成2000ms地层反射系数时间序列(见图5a，仅显示1 000ms)，采用30 Hz混合相位雷克子波(见图6 标号①)，两者褶积产生一道地震记录(见图5b)，再加入一定量的白噪声，生成含噪声的地震记录。

(a.地层反射系数 Reflection coefficientb.合成地震记录 Synthetic seismogram)

图5仿真模型的建立

Fig.5The establishment of simulation model

图6和图7分别是方法一(1.1构造方法)和方法二(1.2构造方法)提取子波的结果。其中，图6-7标号①为时域理论子波，图6标号②③④⑤⑥⑦⑧⑨和图7标号②③④⑤分别是按照方法一和方法二构造的理论伪子波和提取伪子波，每一个标号对应着两道数据，第一道为理论伪子波，第二道为提取伪子波；图6标号⑩和图7标号⑥⑦⑧⑨分别为方法一和方法二的理论子波和提取子波，其第一道为理论子波，第二道为提取子波(见图6a红色曲线)。

这里须要说明一下的是，只输入一道地震记录，理论子波只有一个，而这里得到4个估计子波，理论上这4个估计子波没有任何差异，都等于理论子波，但由于伪子道的噪声水平不一样，可能导致4个子波存在差异，一般认为与其它子波相似性较好的估计子波是准确的。所以，在使用估计子波时，既可以挑选一个与其它相似性较好的子波，也可以剔除估计效果差的子波后，求取平均。图6和图7的a、b、c分别为信噪比为50、10和0db时子波提取的结果，图下部分是上部分一一对应的振幅谱。

可以看出，在信噪比为50和10db时，2种方法都能获得较好的结果，当信噪比为0db时，方法一结果与理论子波差别较大，而方法二子波时域形态和振幅谱都与理论子波符合较好(见图7c红蓝线之间)，说明本文提出的第二种方法抗噪能力较强，且优于方法一。

低信噪比时，方法一提取的伪子波高频部分会有较大缺失(见图6c红线和蓝线之间)，这是由于重构信号的层位越低，相对噪声含量越大，信噪比越低(见图4)，子波提取效果也就越差。第二种方法在选取高信噪比小波层位构造伪子波时，既要注意子波之间的差异性，又要权衡伪子道的信噪比，见图7b红色曲线所示的伪子波，其与其它伪子波保持较大的差异，但主频率比真实地震信号高很多，所以，该伪子道信噪比较低，提取效果也较差。但这种方法的性能取决于伪子波两两之间的最大差异，理论上所有提取的子波都是相同的。当有个别坏道存在时，也不会影响整个子波提取的精度。

4实际地震资料应用

图8和9为某海域的叠后地震资料(见图10a，仅部分显示)采用方法一(1.1构造方法)和方法二(1.2构造方法)和井震联合提取子波的结果。图8标号①②③④⑤⑥⑦⑧是采用db1基小波，按照方法一进行7次分解，重构每一层位信号(8道)组建PSIMO系统后，估计的伪子波结果。图9标号①②③④是分别采用db1、db2、db3、db4基小波，按照方法二进行3次分解，重构第3、4、2、4层位信号(4道)组建成PSIMO系统后，估计的伪子波结果。图8标号⑨和图9标号⑤⑥⑦⑧(蓝色)分别是方法一和方法二提取的地震子波。图8标号⑩和图9标号⑨(红色)为井约束条件下，确定性方法提取的子波，图下部分为上部分一一对应的振幅谱。

通过图8和9对比可知，这两种方法与井约束确定性方法，提取子波的时域波形和振幅谱都比较一致，但高频部分，前者没有后者丰富。图9是将一个地震道，构造成一个伪单输入四输出系统，而每一个伪子道都含有一个互素的伪子波，故能估计出4个伪子波和子波，但在理论上，这4个子波是一致的，都等于实际子波。图10是方法二和井约束确定性方法提取的多个子波(图9标号⑤⑥⑦⑧⑨)与标准子波(令图9标号⑤为标准子波)相减，得到的估计子波残差。图10标号①为标准子波，标号②③④⑤⑥分别对应图9标号⑤⑥⑦⑧⑨的子波残差。可以看到，方法二提取出的4个子波，残差都很小，标号②④⑤几乎为0，说明4个提取子波几乎无差异，与理论相符合。相对地，标号③和⑥的残差稍大，③是由于构造伪子波时，重构层位较高(db3基小波，层位2)，导致主频远高于地震信号(见图9标号③)，信噪比相对较低，导致估计结果误差较大；⑥是由于确定性子波估计方法，加入了井资料，而测井资料的分辨率高，频带宽，故估计子波也更加准确，且分辨率高。

若提取的子波与实际情况符合，则对地震资料进行反褶积、反演等处理，可提高地震资料的分辨能力。图10b、c、d是分别将方法一(见图8标号⑨)、方法二(见图9标号⑧)和井震联合法(见图9标号⑨)提取的子波，作为已知子波输入，按道的顺序对原始地震数据(见图11a)进行频率域除法反褶积后的剖面。通过图像对比可以看到，这三种方法提取的子波反褶积后的结果，都提高了地震剖面的分辨能力：(1)使剖面的同相轴更加精细，可放大高清剖面进行比较；(2)在一定程度上，使不连续同相轴变得更加连续。如图11a所示，一条贯穿CDP标号1～150的不连续同相轴(见深橙色曲线)，在蓝色圆圈处存在明显两处中断，但在图11b上却只存在一处中断，图c和d上不存在中断(见放大蓝色圆圈处)；(3)使不清晰、不平整或者地层太薄无法分辨的同相轴，变得清晰、平整、可分辨。图12a、b、c、d 是图11a、b、c、d鲜橙色矩形框内部分剖面的放大显示。可以看到，三种方法的提取子波对剖面反褶积处理后，使原始资料某些区域不够平整的同相轴，变得更加清晰平整(见黑色虚线标出处)，甚至能分辨出更精细的地层(见褐色矩形框内)。

(a.地震剖面 Seismic profile； b.方法一提取子波反褶积剖面 Deconvolution profile using extracted wave of method 1； c.方法二提取子波反褶积剖面 Deconvolution profile using extracted wave of method 2； d.井震联合法提取子波反褶积剖面Deconvolution profile using extracted wave of well seismic joint method)

图11原始剖面和不同方法提取子波反褶积剖面对比

Fig.11Comparison between seismic section and deconvolution sections via different wavelets extracted by various methods

5结语

针对SIMO系统子波提取方法假设条件难满足问题，笔者利用地震信号的频域性质，运用二进正交小波分解重构理论和Mallat算法思想，初步探讨了两种构建PSIMO系统的方法，也推导了相应的子波提取算法，一定程度上补充了SIMO系统提取子波的理论，也为SISO系统向SIMO系统转化提供了方案。这两种构建PSIMO系统方法也各有一定的优势：第一种利用了Mallat算法能将信号分解且重构信号的和等于初始信号的性质，避免了反褶积运算；第二种利用信号和噪声在小波层位上的分布差异，构建高信噪比的PSIMO系统，使提取子波得更加准确。本文提出的先构建PSIMO系统，再进行子波估计算法，既不需要假设地震子波相位和反射系数分布规律，也不需要假设地震道之间反射系数的相同性，真正实现了无任何假设的二阶累积量混合相位子波盲提取。模型试验和实际应用证明了方法是有效的，且精度较高，抗噪能力强，具有较大应用价值。

参考文献：

[1]戴永寿, 王俊岭, 王伟伟，等. 基于高阶累积量ARMA模型线性非线性结合的地震子波提取方法研究 [J]. 地球物理学报, 2008, 51(6): 1851-1859.

DAI Yong-Shou, WANG Jun-Ling, WANG Wei-Wei, et al. Seismic wavelet extraction via cumulant-based ARMA model approach with linear and nonlinear combination [J]. Chinese J Geophys (in Chinese), 2008, 51(6): 1851-1859.

[2]杨培杰, 潘勇, 穆星，等. 子空间法单输入多输出系统混合相位地震子波提取 [J]. 中国石油大学学报(自然版), 2010, 34(1): 41- 45.

YANG Pei-Jie, PAN Yong, MU Xing, et al. Mix-phase seismic wavelet extraction of SIMO system by subspace method [J]. Journal of China University of Petroleum, 2010, 34(1): 41-45.

[3]李军红, 张建中, 黄忠来，等. 基于倒双谱的地震子波估计方法 [J]. 中国海洋大学学报(自然版), 2014, 44(11): 67-73.

LI Jun-Hong, ZHANG Jian-Zhong, HUANG Zhong-Lai, et al. A method for seismic wavelet estimation based on the bicepstrum of seismic data [J]. Periodical of Ocean University of China, 2014, 44(11): 67-73.

[4]乐友喜, 王才经. 任意相位子波的分形反褶积方法 [J]. 石油地球物理勘探, 1996, 31(6): 826-834.

Le Y X, Wang C J. Fractal deconvolution of any-phase wavelets [J]. Oil Geophysical Prospecting, 1996, 31(6): 826-834.

[5]赵秋亮, 李录明, 罗省贤. 基于分形方法的地震子波提取及应用 [J]. 石油物探, 2005, 44(1): 7-11.

ZHANG Qiu-Liang, LI Lu-Ming, LUO Sheng-Xian. Seismic wavelet extraction and application based on fractal technique [J]. Geophysical Prospecting for Petroleum, 2005, 44(1): 7-11.

[6]张贤达, 保铮. 通讯信号处理 [M]. 北京：国防工业出版社，2000.

ZHANG Xian-Da, BAO Zheng. Basis for communication precess [M]. BeiJing: National Defence of Industry Press, 2000.

[7]马建仓. 盲信号处理 [M]. 北京：国防工业出版社，2006.

MA Jian-Cang, Blind Signal Processing [M]. Beijing: National defence of Industry Press, 2006.

[8]Zhang X D，Zhang Y S. FIR system identification using high order cumulants alone. IEEE Trans on SP, 1994, 42(10): 2854-2858.

[9]Ulrych T J， Velis D R， Sacchi M D. Wavelet estimation revisited[J]. The Leading Edge, 1995, 14(11): 1139-1143.

[10]李国发, 彭苏萍, 高日胜，等. 复赛谱域提取混合相位子波的方法[J]. 天然气工业, 2005, 25(1): 85-87.

LI Guo-Fang, PENG Su-Ping, GAO Ri-Sheng, et al. Method of mixed phase wavelet extraction in cepstrum domain [J]. Natural Gas Industry, 2005, 25(1): 85-87.

[11]Petropulu A P et al. Phase reconstruvtion from bispectrum slices [J]. IEEE Trans on SP, 1998, 46(2): 527-530.

[12]Pan R L et al. Phase reconstruction in the trispectrum domain [J]. IEEETrans on Acoustics, Speech, andSP, 1987, 36(6): 895-897.

[13]李大卫, 尹成, 熊晓军，等. 高阶谱混合方法地震子波估计及处理 [J]. 地球物理学进展, 2005, 20(1): 29-33.

LI Da-Wei, YI Cheng, XIONG Xiao-Jun, et al. A hybrid high order spectrum method for seismic wavelet estimation and processing [J]. Progress in Geophysics, 2005, 20(1): 29-33.

[14]谢桂生, 石玉梅，魏野. 双谱地震子波估计 [J]. 西南石油学院学报, 2000, 22(3): 25-28.

XIE Gui-Sheng, SHI Yu-Mei, WEI Ye. Wavelet estimation based on bispectrum [J]. Journal of Southwest Petroleum Institute, 2000, 22(3): 25-28.

[15]Misra S, Sacchi M. Wavelet estimation by non-linear optimization of all pass operators[J]. CSEG RECORDER. 2006, 38-42.

[16]Porsani M J, Vrsin B. Mixed-phase deconvolution [J]. Geophysics, 1998, 63(2): 637-647.

[17]Ursin B, Porsani M J. Estimation of an optimal mixed-phase inverse filter [J]. Geophysical Prospecting, 2000, 48(4): 663-676.

[18]Buland Omre H. Bayesian wavelet estimation from seismic and well data [J]. Geophysics, 2003, 68(6): 2000-2009.

[19]张广智, 刘洪, 印兴耀. 井旁道地震子波精细提取方法 [J]. 石油地球物理勘探, 2005, 40(2): 158-162.

ZHANG Guang-Zhi, LIU Hong, YIN Xing-Yao. Method for fine picking up seismic wavelet at uphole trace [J]. Oil Geophysical Prospecting, 2005, 40(2): 158-162.

[20]Lang Tong. Blind identification and equalization based on second-order statistics: a time domain approach [J]. IEEE Transacticins on Information Theory, 1994, 40(2)： 340-349.

[21]蒋静. 基于子空间的二阶统计量盲信道辨识算法研究[D]. 郑州：郑州大学, 2010.

JIANG Jing. Blind Channel Identification Based on Subspace Method of Second-order Statistics[D]. Zhengzhou：Zhengzhou University, 2010.

[22]杨培杰. 地震子波盲提取与非线性反演[D]. 北京：中国石油大学, 2008.

YANG PeiJie. Seismic Wavelet Blind Extraction and Non-Liner Inversion[D]. Beijing： China University of Petroleum(East China), 2008.

[23]邱娜. 地震子波分解与重构技术研究[D]. 青岛：中国海洋大学, 2012.

QIU Na. Research on Seismic wavelet Decomposition and Reconstruction Technology[D]. Qingdao： Ocean University of China, 2012.

[24]Eric Moulines, Pierre Duhamel. Subspace Methods for the Blind Identification of Multichannel FIR Filters [J]. IEEE Transactions on Signal Processing, 1995, 43(2)： 516-525.

[25]何子苏, 夏威. 现代数字处理及其应用 [M]. 北京：清华大学出版社, 2004.

HE Zi-Su, XIA Wei. Modern digital processing and its application [M]. Beijing: Tsinghua University Press, 2004.

[26]Eric Moulines, Pierre Duhamel. Subspace methods for the blind identification of multichannel FIR filters [J]. IEEE Transactions on Signal Processing, 1995, 43(2)：516-525.

[27]Xia W, He Z H, Liu B Y, et al. Adaptive multichannel blind identification using manifold optimization [J]. Signal Processing, 2008(88): 1595-1605.

[28]周伟. 基于MATLAB的小波分析应用(第2版) [M]. 西安：西安电子科技大学出版社出版, 2010.

ZHOU Wei. Wavelet analysis applications based on MATLAB(second edition)[M]. XiAn: XiAn Electronic Science & Technology University Press, 2010.

[29]葛哲学, 沙威. 小波分析理论与MATLAB R2007实现 [M]. 北京: 电子工业出版社, 2007, 10: 76-85.

GE Zhe-Xue, SHA Wei. Wavelet analysis theory and implementation of R2007 MATLAB[M]. BeiJing: Electronic Industry Press, 2007, 10: 76-85.

责任编辑徐环

Based on the Pseudo Single-Input Multi-Output System to Extract Seismic Wavelet

ZHANG Han-Yu1,2, LIU Huai-Shan1, XING Lei1, SHI Xu-Liang1, LEI Chao-Yang1

(1.Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, China; 2.Institute of Deep-sea Science and Engineering, Chinese Academy of Sciences, Sanya 572000, China)

Abstract:The method of extracting seismic wavelet based on the Single-input Multi-output (SIMO) System, requires reflection coefficients to be the same as the others and wavelets to be different from the others. In other words, it unreasonably assumes that all the difference of seismic record is caused by multi-wavelet and has nothing to do with reflection coefficients. In order to avoid these assumptions, Aiming at the character of seismic signal and using the thinking about Mallat algorithm of the Discrete Wavelet Transform, this paper makes a preliminary discussion about two methods of building Pseudo Single-Input Multi-Output System (PSIMO), and then deduces the algorithm of extracting seismic wavelet with noise subspace method in PSIMO system. The results of simulation and application demonstrate that those methods are effective and characterized by strong stability to resist noise.

Key words:PSIMO； subspace； mallat algorithm； wavelet extraction

基金项目：❋ 国家自然科学基金项目(41176077 、41230318和41304096)；教育部博士点基金项目(20130132120014)；国家高技术研究与发展计划项目(2013AA092501)资助

收稿日期：2015-02-03；

修订日期：2015-04-05

作者简介：张汉羽(1989-)，男，硕士生，主要从事海洋地震勘探研究。E-mail: 824284715@qq.com ❋❋通讯作者：E-mail: xingleiouc@ouc.edu.cn

中图法分类号：P315.3

文献标志码：A

文章编号：1672-5174(2016)06-074-10

DOI：10.16441/j.cnki.hdxb.20150029

Supported by The National Natural Science Foundation of China(41176077、41230318、41304096)、Ph.D. Programs Foundation of Ministry of Education of China(2013132120014) and The National High Technology Research and Development Program of China(2013AA092501).