加速度计交叉耦合系数高精度标定

徐仕会

(中航工业西安飞行自动控制研究所,陕西 西安　710065)

加速度计交叉耦合系数高精度标定

徐仕会

(中航工业西安飞行自动控制研究所,陕西 西安710065)

摘要:为了在1g重力场用转台标定惯性导航系统加速度计交叉耦合系数,提出基于正交多位置递推滤波算法标定加速度计的方案,通过建立正交多位置标定模型,抑制了转台误差对标定精度的影响,设计基于马尔科夫递推估计滤波算法,克服了一般最小二乘集中估计中多维矩阵求逆算法误差。仿真结果表明通过28位置标定,加速度计交叉耦合系数标定精度可达到10-7g·g-2(RMS)量级。

关键词:加速度计标定；交叉耦合系数；递推滤波

惯性导航系统具有自主、隐蔽、导航信息全的特点,适于海、陆、空、天全天候全空间导航,是导弹、飞机、舰船的重要导航设备。惯性导航系统是基于测量载体的运动角速度和加速度,通过信息处理、导航解算、自动控制实现载体在三维空间的导航。加速度计是惯性导航系统的关键器件,惯导系统需要持续实时通过积分加速度计信号进行导航位置解算,加速度计性能直接影响惯导系统的精度,因此对加速度计的指标要求较高。加速度计的零偏、刻度系数、交叉耦合系数、二次项系数、高阶项系数对加速度计性能有直接影响,因此必须对这些参数进行精确标定和补偿,通常加速度计的零偏、刻度系数、交叉耦合系数可以在实验室1g重力场环境下标定,二次项系数、高阶项系数在离心机高加速度激励下标定。

在交叉耦合系数的标定中,转台的姿态误差、加计夹具的安装误差对加速度计交叉耦合系数的标定影响较大,对于要求10-6g的标定精度量级,其对转台和夹具的姿态精度要求在1″量级,目前的设备和工艺条件较难实现。另一方面加速度计需要标定的参数项多,通常的测试是采用多点测量集中最小二乘来估计参数的,为了提高估计精度需要增加测点数,从而使得集中最小二乘估计时需要计算高维矩阵求逆,这样会增加计算量和计算误差。因此必须研究如何通过标定方案和算法的设计解决加速度计交叉耦合系数的高精度标定问题。文献[1]提出一种无需专用转台标定惯导系统加速度计的方法,其主要研究了基于惯导系统的多位置测试标定加速度计零偏、刻度系数及安装误差,模型中忽略了加速度计交叉耦合系数项。文献[2]提出采用奇异值分解SVD(singular value decomposition)对加速度计信号作降噪处理再用总体最小二乘估计辨识加速度计参数的方案,从理论上分析了加速度计噪声信号的SVD抑制,其需构造加速度计采样序列的Hankel矩阵,随着采样点的增加Hankel矩阵维数较大计算量大。文献[3]用协方差相关性分析了加速度计零偏、刻度系数及安装误差参数的辨识特性,其模型中未包含加速度计交叉耦合系数项。文献[4]提出正交双加速度计通过D-最优信息矩阵和三角函数正交化,设计了交叉耦合系数D-最优标定试验方法,计算复杂，不便于工程化应用。文献[5]提出转台正交多位置加倾斜转台多位置方式,通过非线性模型和参数分步标定线性化,设计了交叉耦合系数标定方案,达到了较高的标定精度,其标定流程较复杂设备成本高。文献[6]提出加速度计36位置全组合测量加三角函数谐波分析的方式设计了加速度计标定方案,其集中估计计算量大。本文主要通过建立正交多位置标定模型,抑制转台误差对标定精度的影响,设计马尔科夫递推估计滤波算法,克服一般最小二乘集中估计中多维矩阵求逆算法误差,减少数据存储量,便于工程化应用。

1标定方案及模型建立

1.1加速度计模型

比较完整的加速度计模型通常包含非线性高次项和交叉耦合项[7],其模型公式为

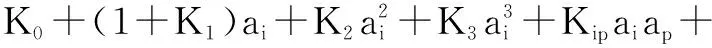
Kioaiao+Kopaoap

(1)

式中，As为加速度计输出;K0为加速度计零偏;K1为刻度系数误差;K2为二次项系数;K3为三次项系数;Kip为与摆轴向的交叉耦合项系数;Kio为与输出轴向的交叉耦合项系数;ai为加速度计输入轴方向加速度;ap为加速度计摆轴方向加速度;ao为加速度计输出轴方向加速度。

1.2加速度计交叉耦合系数标定模型

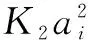
图1　正交安装加速度计相对位置关系

图2　加速度计测试位置

对A加速度计各轴向的激励加速度为

(2)

A加速度计输出为

As1=KoA-(1+K1A)gcos(θ+δθ+δ0)-

g2KipAsin(θ+δθ+δ0)cos(θ+δθ+δ0)

(3)

对B加速度计各轴向的激励加速度为

(4)

B加速度计输出，有

(5)

其中，θ为转台的姿态角,δθ为转台和夹具的水平姿态误差角,δ0为A加计对水平轴的安装误,β0为B加计对A加计的不正交安装误差角,δθ、δ0、β0均为小角度。

对式(3) 、 (5)两边分别平方,忽略二阶以上小量,可得到

(6)

(7)

由式(6)、(7)相加，得

(8)

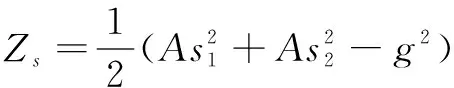
Zs=KoBgsinθ-KoAgcosθ+K1Ag2cos2θ+K1Bg2sin2θ+g3KipAsinθcos2θ+g3KipBcosθsin2θ+g2β0sinθcosθ

(9)

转动转台轴可得多个角位置测量的Zs序列[Zs1、Zs2、… Zsn],建立矩阵方程模型:

Zs=HX+W

(10)

X=[KoBKoAK1AK1BKipAKipBβ0]T,Zs=[Zs1Zs2…Zsn]T,H为n阶测量矩阵,W为量测噪声。

1.3加速度计递推滤波估计标定算法

在得到n个位置测量数据后对模型(10)作一般最小二乘估计，有

(11)

可得到两个加速度计的标定参数估计。由于待估计参数有7个,测点至少需要7个,通常情况下得到较高的估计精度,测量位置点应该在10个以上,使得矩阵H维数在10阶以上从而使集中最小二乘估计需进行高阶矩阵求逆。

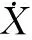
(12)

其中，X为待估参数向量;Hck为量测阵;Rc为量测噪声阵;Pc为滤波估计均方误差阵。

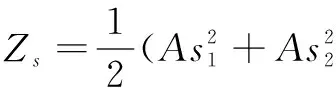
2仿真验证

仿真条件:A加速度计KoA=3×10-5g,K1A=4×10-5,KipA=5×10-5g/g2;B加速度计KoB=6×10-5g,K1B=7×10-5,KipB=8×10-5g/g2;转台和夹具的水平姿态误差角δθ=10″;初始位置A加计对水平轴的安装误差角δ0=10″;B加计对A加计的不正交安装误差角β0=5″,转台和夹具的初始位置角θ0=5°,转台测量位置角度增量13°,测量位置数28。用Matlab编制仿真软件得到以下仿真结果如表1及图3-图9。

表1　加速度计参数标定滤波估计表

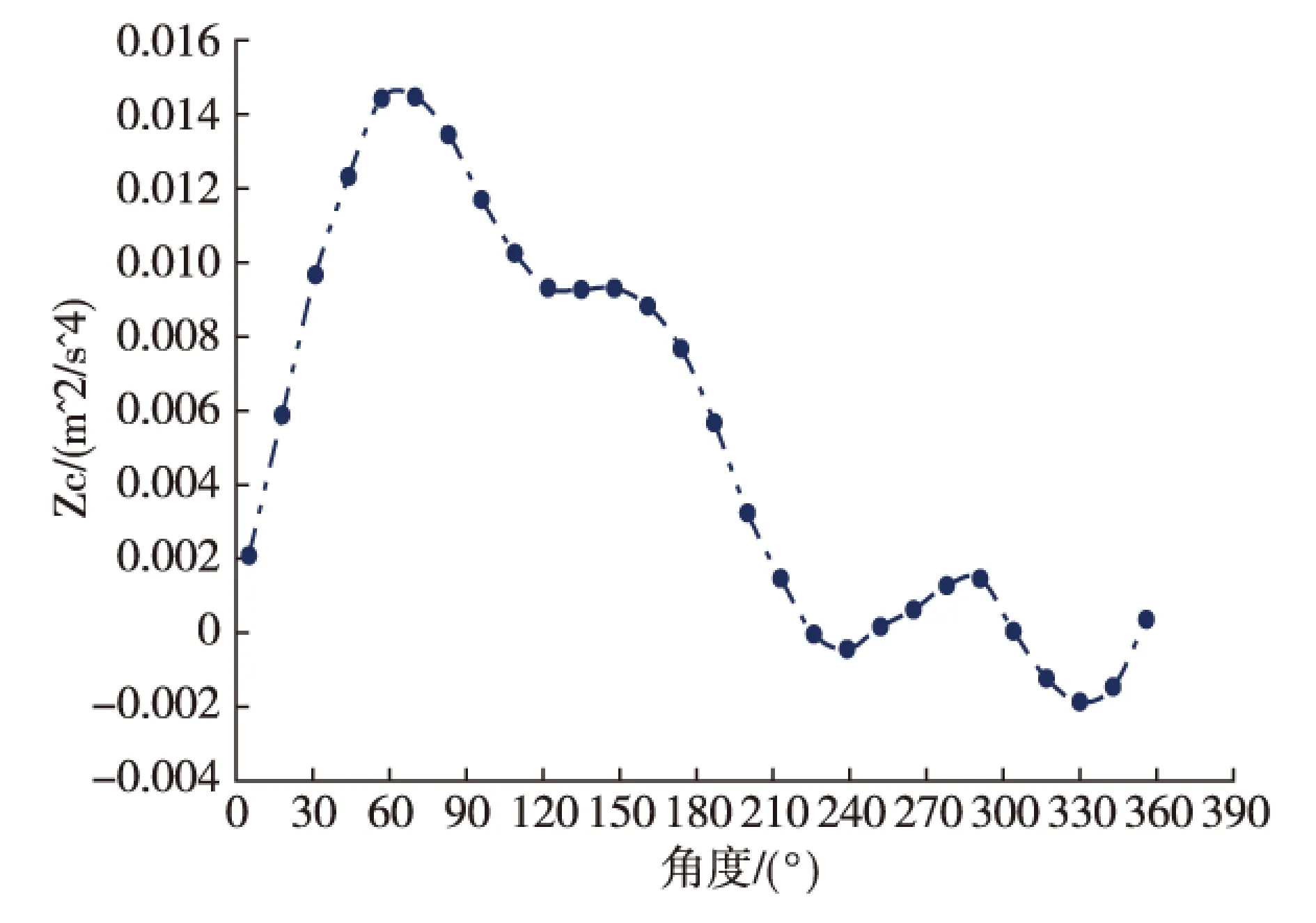
图3　观测量曲线

图4　A加速度计交叉耦合系数估计曲线

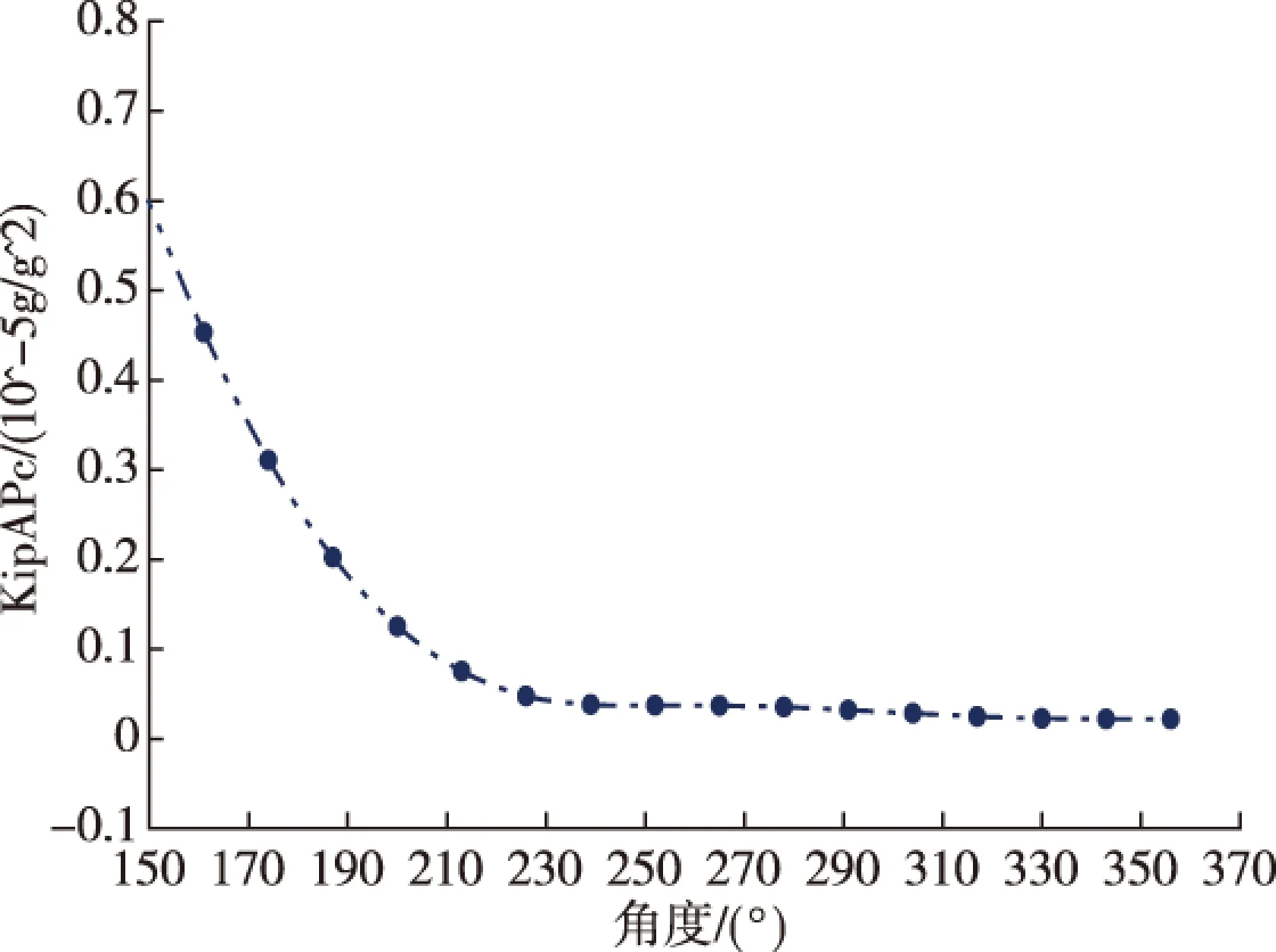
图5　A加速度计交叉耦合系数估计误差均方根曲线

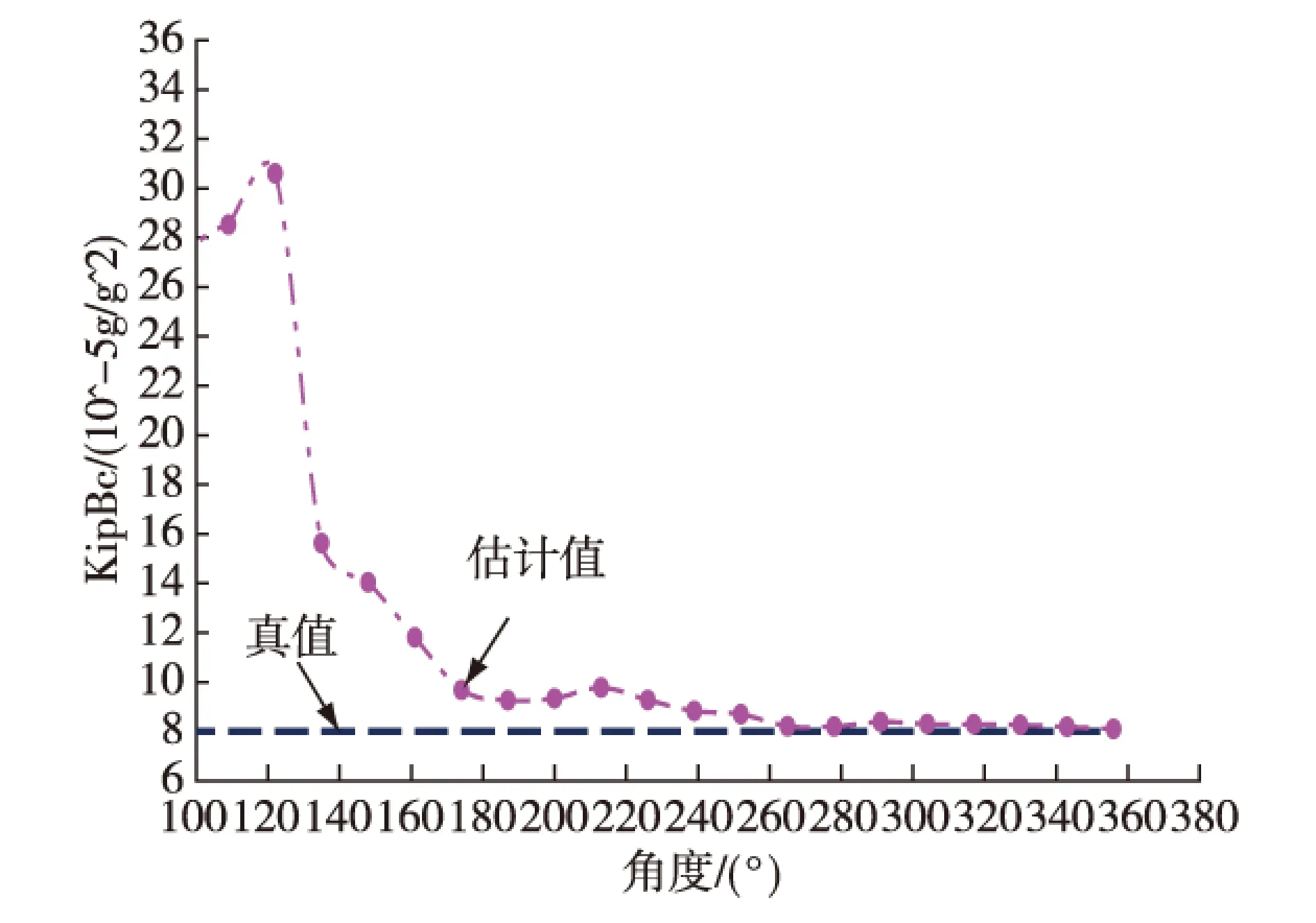
图6　B加速度计交叉耦合系数估计曲线

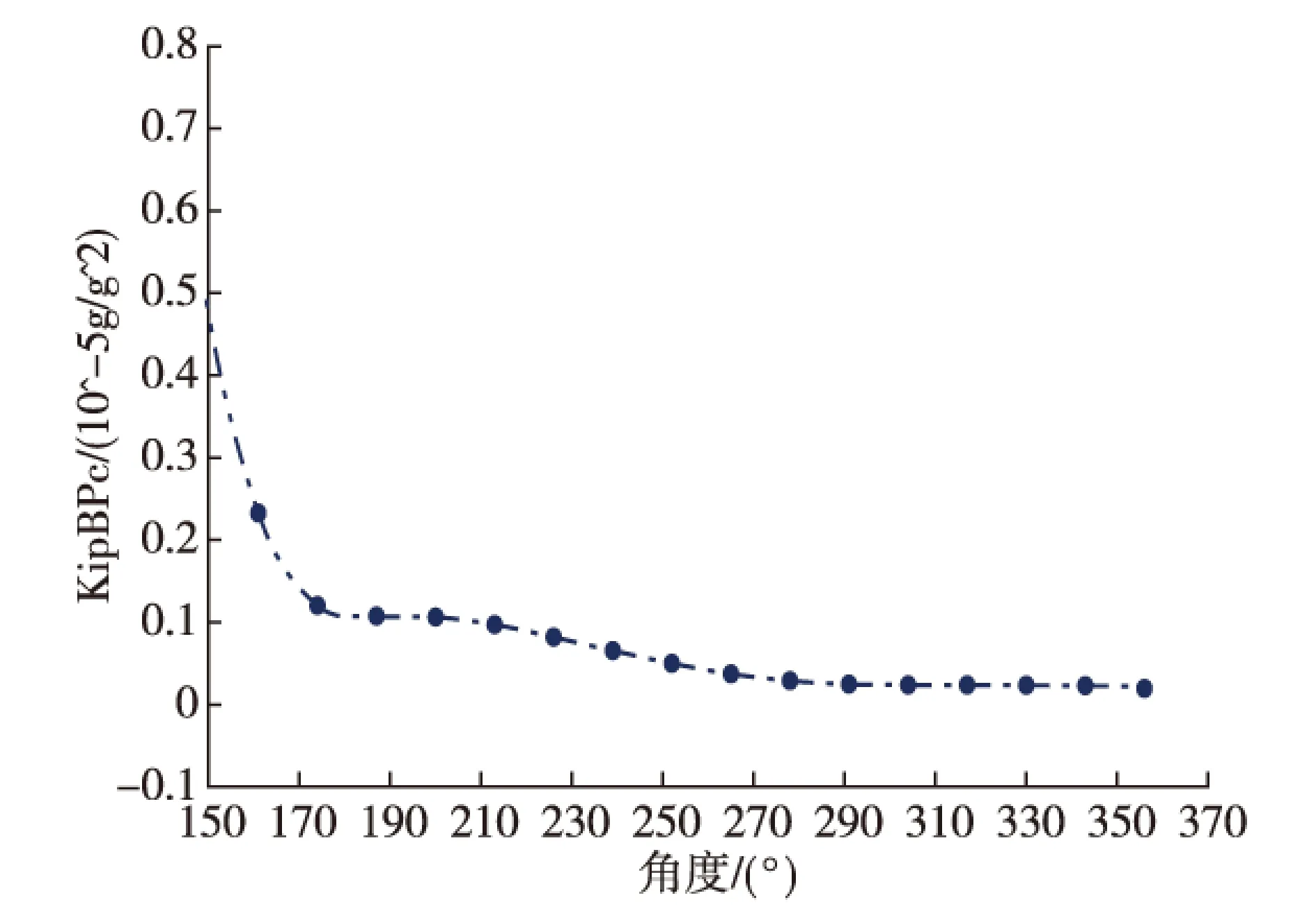
图7　B加速度计交叉耦合系数估计误差均方根曲线

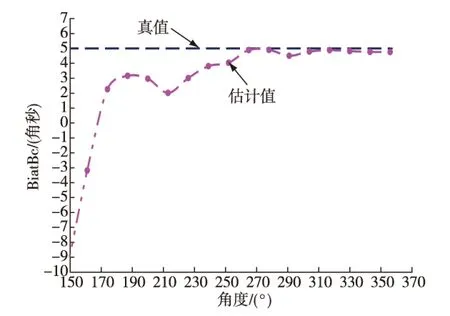
图8　A、B加速度计不正交角度估计曲线

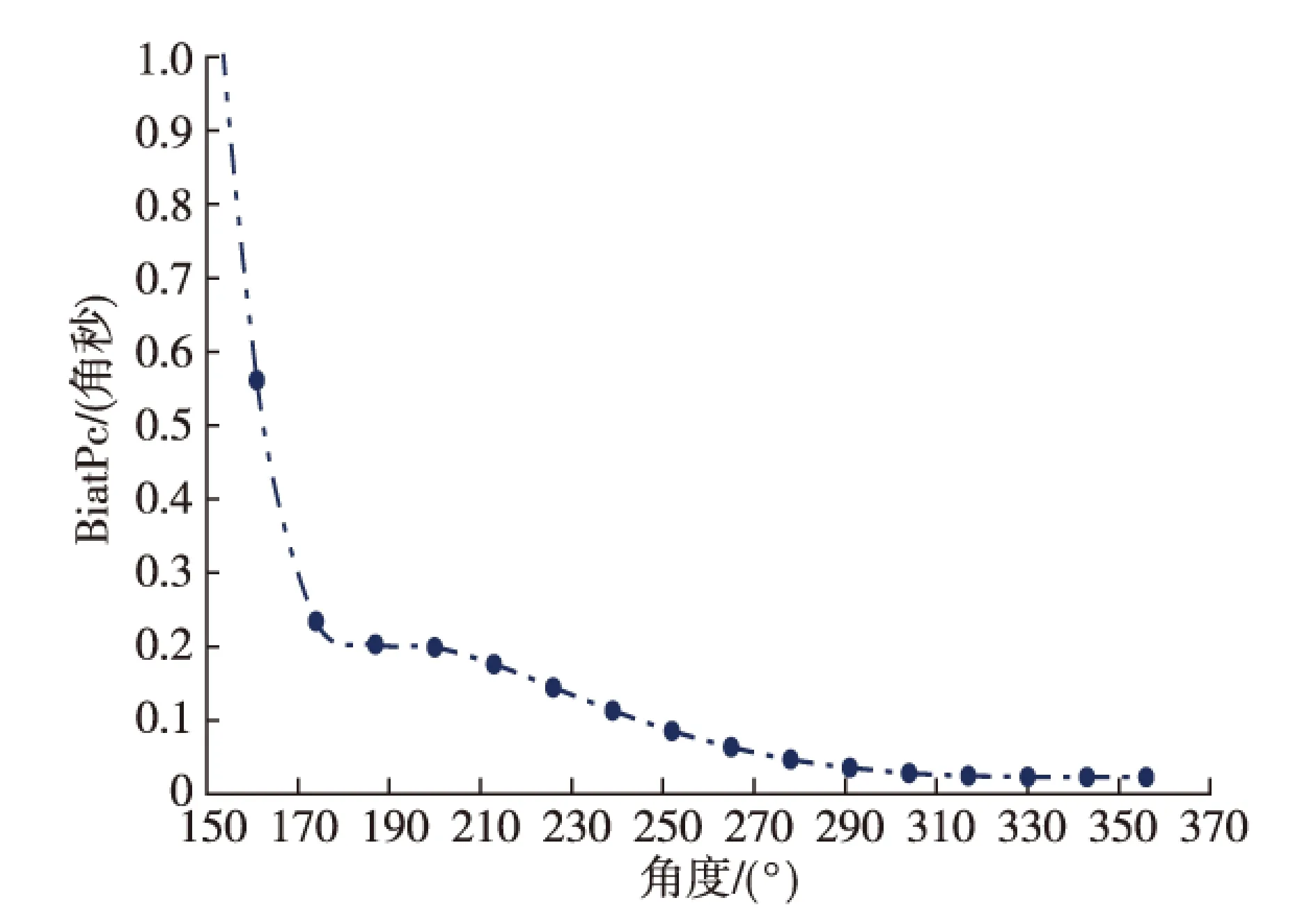
图9　A、B加速度计不正交角度估计误差均方根曲线

3结论

1) 通过建立1g重力场加速度计交叉耦合系数Kip标定模型,采用正交多位置测量,可以消除转台误差对交叉耦合系数标定精度的影响。

2) 增加观测位置对提高标定精度是有益的,设计的递推滤波估计算法,克服了一般最小二乘估计算法中的大矩阵求逆误差,减少了数据存储量及计算量,便于测控计算机在线实时递推估计和工程化实施。

3) 设计的正交多位置递推滤波估计标定模型对于加速度计间的非正交安装误差也可进行标定。

4) 对于加速度计的Kio交叉耦合系数可以通过改变安装方式采用同样的算法标定。

5) 仿真结果表明:加速度计交叉耦合系数标定滤波估计在18位置测量后收敛,28位置标定精度可以达到10-7g/g2(RMS)的量级;加速度计非正交安装误差标定滤波估计在21位置测量后收敛,28位置标定精度可以达到10-2″(RMS)的量级。

参考文献:

[1]陈剑,孙金海,李金海,等.惯性系统中加速度计标定方法研究[J].微电子学与计算机,2012,29(8):130-133.

[2]李强,陈雪冬,徐伟.加速度计信号奇异值分解滤波与参数辨识[J].自动化仪表,2014,35(9):16-20.

[3]刘璠,魏宗康.捷联惯性组合误差模型相关性分析方法[J].中国惯性技术学报,2014,22(5):567-571.

[4]蒋效雄,刘雨,苏宝库.高精度加速度计重力场标定试验方法[J].吉林大学学报,2010,40(1):287-292.

[5]杨杰,吴文启,练军想.激光陀螺捷联系统高精度加速度计非线性模型参数标定[J].中国惯性技术学报,2010,18(5):625-632.

[6]任顺清,冯士伟,马向斌.加速度计的全组合标定方法[J].中国惯性技术学报,2007,15(6):760-764.

[7]IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers[S].IEEE Std836-2001, 29-34.

[8]徐仕会,冯培德,雷宏杰.惯性导航系统扰动基座对准仿真研究[J].计算机仿真,2008,25(11):88-90.

Precise Calibration for Accelerometer Cross Coupling Coefficient

XU Shi-hui

(AVIC Xi’an Flight Automatic Control Research Institute, Xi’an 710065, China)

Abstract:For calibrating the cross coupling coefficient of inertial navigation system accelerometer in 1g gravity field by means of turntable precisely, a calibration method based on recursive filter at perpendicular multi-positions has been presented in this paper. The influence of turntable error has been restrained effectively in virtue of a perpendicular multi-positions calibration model. An algorithm filter based on Markov recursive estimation is established. The multi-dimensions matrix inverse algorithm error which is existed in least square estimation has been overcome. The simulation results show that a 10-7g/g2(RMS) calibration precision of cross coupling coefficient can be reached by dint of twenty-eight positions calibration.

Key words:accelerometer calibration； cross coupling coefficient； recursive filter

文章编号：1673-3819(2016)03-0136-04

收稿日期：2015-11-16

作者简介：徐仕会(1963-)，男，贵州思南人，博士，研究员，研究方向为导航、制导与控制。

中图分类号:TN967

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.03.027

修回日期： 2016-03-01