基于改进Markov模型软件测试策略

李泽雪,李相民,薛　亮

(1. 海军航空工程学院,山东烟台　264001; 2. 海军装备研究院，北京　100161)

基于改进Markov模型软件测试策略

李泽雪1,李相民1,薛亮2

(1. 海军航空工程学院,山东烟台264001; 2. 海军装备研究院，北京100161)

摘要:针对已有软件测试Markov模型与工程实践不符的情况,通过引入软件需求覆盖率改进Markov模型。在改进的Markov模型基础上,本文以软件测试过程中测试总代价最小为控制目标, 采用交叉熵方法修正测试剖面, 由优化测试剖面生成测试用例序列。仿真结果表明这种方法能够有效地降低软件测试总代价, 是一种有效的软件测试方法。

关键词:软件测试;交叉熵法;覆盖率

软件测试是软件生存周期中的一个重要组成部分,是保证软件质量的重要阶段之一。软件测试中,由于穷举法的工作量太大[1],成本太高,在实际操作中一般不采用穷举法。如何在对被测系统进行有效测试的基础上,通过优化测试用例的选用尽可能地减少测试成本,是软件测试领域中需要研究的一个关键性问题。

随着测试剖面和Markov模型等概念的提出,使软件测试在理论上有了一个大进步。基于测试剖面或Markov模型对测试用例进行选取,能大幅提高测试用例选取的有效性。常见选取方式有:随机选择[2],这种方式根据测试剖面随机的选择测试用例;重要性测试,根据指定的权重大小选择测试用例,测试那些用户使用可能性高的路径。

由于上述的测试方法没有明确的优化目标,成本都比较高。因此研究一种新的测试方法,对于降低软件测试的总成本具有重要意义。

文献[3]在解决测试资源分配问题时,文献[4]在采用搜索的方法测试时,文献[5]在提出改进测试模型时,文献[6]讨论Markov模型在软件测试中的应用时,都提出了明确的优化目标,证明这些测试方法在理论上十分有效,但这些测试方法与实际测试技术缺乏有效的切合点,还没有在工程实践中得到应用。

为了结合工程实践,本文将测试需求覆盖率引入到传统的Markov模型中,并在传统软件测试方法学习的基础上, 利用交叉熵法优化软件测试剖面,以软件测试过程的总费用最小为控制目标,优化整个测试过程。

1Markov决策过程

Markov决策过程是一类重要的随机过程,它最早是由俄国数学家Markov在1907年提出,Markov过程的核心是它的Markov性,即:如果系统在t0时刻所处的状态是已知的,那么系统在t0时刻后将达到的状态完全由系统在t0时刻所处的状态决定,与系统在t0时刻之前所处的状态没有关系。这种“现在”已知的条件下,“过去”和“将来”相互独立的特性叫做无后效性，也称为Markov性,具有这种性质的随机过程叫做Markov过程[7]。这种性质可以被用于模拟软件测试的过程:软件的下一状态只与软件当前的状态有关。

Markov决策过程主要包括决策时刻、状态、决策、转移概率和报酬这五个属性。可由一个五元数组表示(S,A,{A(t)|st∈S},F,W),其中用S表示系统所有可能的状态集合,即状态空间,用A表示所有可用的决策组成的决策集,A也称为决策空间,若在某一决策时刻,系统状态st∈S,这时的所有可用决策可由集合{A(t)|st}表示,并且从集合{A(t)|st}中选取决策a作为这一时刻所采用的决策。该模型是一个在t=0,1,2,…上随机可控的系统,在某一决策时刻,系统的状态为st,选取决策at∈A(t)后,会产生这样一个结果:决策者将以代价Wst(A(t))使系统状态由概率分布F(S|s,a)=P{St+1=s,At=a}转移到下一个状态,一旦系统转移到新的状态,系统将会选择新的决策继续循环决策过程。

2基于改进Markov模型的软件测试方法研究

在已有Markov模型中,测试结束的标准主要是所有缺陷都被检测到[8]。相关研究表明这种方法能够取得较好的测试效果。但是,这种测试方法还没有在测试实践中应用。因为在实际测试过程中测试人员不可能知道软件中缺陷的准确数量,所以这种已有的测试方法并不符合实际情况。

在工程实践中,测试人员通常把需求覆盖率作为测试结束的标准,实践证明达到一定覆盖率标准的软件,通常其测试结果比较充分。因此本文将需求覆盖率与软件中剩余的缺陷数一起作为被测软件的状态,并将需求覆盖率和检测到一定数量缺陷作为测试结束标准。

从缺陷数据库中可得被测软件不同版本的缺陷数量情况,由灰色模型预测理论预测软件下一版本的缺陷数。假设被测软件最初至少存在M个缺陷,测试的目标是在测试覆盖率到达100%的情况下至少发现软件中的M个缺陷。在整个测试过程中,如果把每个决策时刻t(t=0,1,2,…)时软件需求覆盖率和软件中的剩余缺陷数当作t时刻系统的状态st,决策是各个时刻t测试用例的选取,而且满足t+1时刻系统的状态st+1只与系统在t时刻所处的状态st和采取的决策at有关。

定义

为了把Markov决策模型运用到软件测试过程中,对被测软件作出如下一些假设:

1) 用Nt表示被测系统t时刻的缺陷数,初始时刻被测系统中至少含有M个缺陷;

2) 用Qt表示被测系统时刻的需求覆盖率,初始时刻需求覆盖率Q0=0;

3) 把每个决策时刻t(t=0,1,2,…)时软件中的剩余缺陷数Nt和需求覆盖率Qt作为t时刻系统的状态St=(Nt,Qt);

4) 在每个时刻只需选取一个决策,并且最多只能发现一个缺陷;

5) 当缺陷被检测到时,则认为被检测到的缺陷被剔除,即如果Nt=j,Zt=1,那么Nt+1=j-1;

6) 用qa表示测试用例a的覆盖率,每使用一个用例,那么Qt+1=Qt+qa;

7) 若没有检测到缺陷,即若Nt=j,Zt=0,则Nt+1=j;

8) 目标状态是St=(0,100%)；

9) 系统在不同状态下都有n个可选决策,用A表示可选的决策集合;

10) 时刻执行决策a后,不论是否检测到缺陷,花费的代价都为Wst,本文主要指测试时间;

11) 不考虑缺陷移除所花费的代价。若用τ表示系统状态到达目标状态时所花费的时间,则有

(1)

(12) 其中,ω表示软件测试方法,由它决定测试过程中测试用例的选取,Eω表示相对于测试方法ω求期望值,WS(At)表示执行选取的测试用例要花费的代价,Jω(N)表示测试过程中产生的总代价的期望值。

那么就可以把软件测试过程当作Markov决策过程,如图1所示。

图1　Markov决策过程

3基于交叉熵法求解测试目标

交叉熵法是一种估计复杂随机网络中小概率事件发生概率的算法,其可以很好地解决组合优化问题,因此近年来受到了广泛的关注。Rubinstein首先创造性地提出了交叉熵法。并且在小概率事件的组合优化模拟中运用了这种方法。文献[9]利用交叉熵法很好地解决了旅行商问题。文献[10]将交叉熵法用于到缓冲区分配问题中。交叉熵法在最大割问题中[11]也体现出极大的优势。交叉熵法的独特优势是定义了一个用来对算法进行快速引导的精确的数学框架。从某种意义上说,交叉熵法是一种基于先期模拟理论的优化学习算法。

用X=(X1,X2,…,Xn)表示测试用例按某个概率分布生成的序列集,其中随机变量Xi=(i=1,2,…,n)按照测试剖面进行选取,用pij表示在状态Nt=i选择决策a的概率,P=(pij)M×K是概率矩阵。定义γ*为采用不同测试方法ω生成测试用例序列X时花费代价Jω的最小值,即

γ*=minJω

(2)

用f(x,u)表示测试用例序列x的联合概率分布,f(x,u)由概率矩阵P唯一确定,那么测试问题则转化为如何使式(2)取优的问题。定义I(Jω≤γ)为测试用例X上不同γ∈R值的示性函数的集合,那么最优选择概率的确定问题可转换为概率估计问题来求解:

(3)

其中,Pu和Eu分别是概率分布f(·,u)的概率测度和期望。

当γ=γ*时,估计l(γ)最直接的方法是采用重要抽样法:根据决策集A上的概率分布g来抽取样本x1,x2,…,xn,则l(γ)的估计为

(4)

显然,当概率分布g取

(5)

时,只需要抽取一个样本,即N=1就能得到1的一个无偏估计形式:

(6)

由上式可以看出,g*(xi)的选取依赖于未知参数l,而l难以确定。所以采用在概率分布f(·,u)的概率分布簇{f(·,υ)}中选取概率分布g的方法来解决这个问题,即选择参数v使得概率分布簇f(·,υ)与概率分布g*(xi)之间差别最小。衡量两个概率分布差别大小的常用测度是Kullback-leibler距离或交叉熵。定义Kullback-leibler距离为

=∫g(x)lng(x)dx-∫g(x)lnf(x)dx

(7)

这样,最优抽样分布的确定问题就转化成确定推断参数υ,使得概率分布簇f(·,υ)与概率分布g*(xi)交叉熵最小的问,即

υ*=argmin-∫g*(x)lnf(x,υ)dx

(8)

然后有

υ*=argmaxEu[I(Jω≤γ)lnf(x,υ)]

(9)

由于测试用例序列x=(a0,a1,…)是根据概率矩阵P生成的,概率矩阵P就是推断参数υ,而测试用例序列x的联合概率分布为

(10)

满足：

(11)

其中，i为测试用例序列x在运行中经历的所有状态,j为测试用例序列x中在状态st=i时选取的决策。

由拉格朗日乘法,建立如下方程:

(12)

(13)

由拉格朗日乘法可得最优的决策选择概率为

(14)

决策选择概率估计为

(15)

在应用交叉熵法时,关键的问题是参数怎么在迭代中被修正。通常参数的修正是在一个两步迭代过程中实现的。

1)适应性修正γt。

2)适应性修正vt

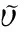
(16)

算法可如下表示:

Begin

Update(p)∥更新测试用例选择概率

pij=1/K∥初始化为均匀分布

While(γt≠γt-1)∥中止条件

{

get(X);∥模拟生成测试序列

Updata(pij)∥更新测试用例选取概率

t++

}

End

算法流程图如图2所示。

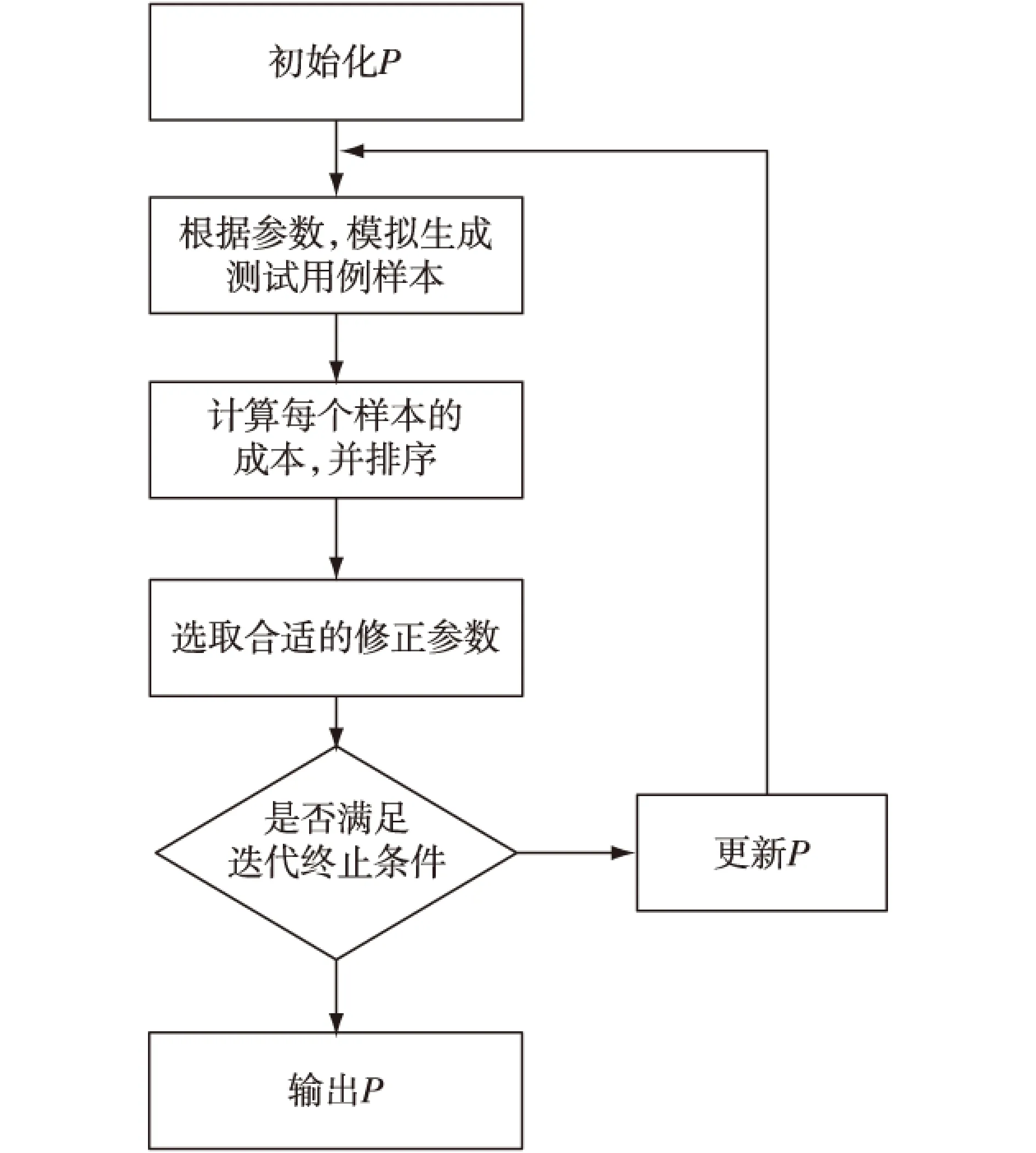
图2　求解最优选择概率流程图

4仿真分析

为验证交叉熵法测试决策选择概率的有效性,本节采用仿真的方法,比较交叉熵法与随机测试的测试总成本。

由灰色预测理论,假设开始时软件中至少含有缺陷数为M=7。决策空间A={1,2,3,4,5,6},相应的缺陷检测率为θ1=0.3,θ2=0.1,θ3=0.2,θ4=0.125,θ5=0.25,θ6=0.15,在不同状态下采用不同行动的测试代价用表1表示。

表1　不同状态s下采用不同行动a的测试成本

测试用例与需求覆盖关系如表2所示。

算法中取N=1000,ρ=0.25,α=0.4时,用交叉熵法进行迭代过程中γ的变化曲线，如图3所示。

图3　参数日γ变化曲线

从仿真结果来看,参数在迭代中不断修正,参数γ的变化趋势不断变小,并且朝着最优值的方向逼近。从生成的最优测试剖面可以看出:优化测试剖面与Ws(a)/θs的比率和测试用例覆盖情况有关,比率较小的决策会被优先选择。因此,这些决策被选择的概率要大于其它行动。这与实际情况[12]是一致的。

表2　测试用例需求覆盖情况

采用优化测试剖面Popt和随机测试分别进行10轮抽样1000次的测试模拟,两种测试方法所需要的平均测试成本如图4所示。

图4　测试成本

5结束语

软件测试的Markov模型将软件测试过程当作一个随机过程来处理。本文给出了一个软件测试的改进Markov决策模型,在原始Markov模型的基础上引入软件需求覆盖率,使模型更适用于工程实践。将软件测试的总费用最小作为控制目标,并且采用交叉熵法来搜索软件测试的最优测试剖面,以优化软件的测试过程。仿真结果表明用这种方法优化得到的测试剖面要优于随机测试方法的测试剖面,它可以显著地减少测试用成本。这种方法使优化软件测试过程研究的实践化向前迈进了一步,为“基于搜索的软件工程”[11]的研究提供了一种新尝试。由于该方法采用的交叉熵法本身具有很强的适应力,只需要处理较少的参数就可以保证算法的收敛性,它比其它方法具有更强的稳健性[13-14],因此这种方法可以在软件测试领域种广泛的运用。

参考文献:

[1]Jeya Mala D, Mohan V, Kamalapriya M. Automated software test optimisation framework Anartificial bee colony optimisation based approach[J]. Source: IET Software, 2010, 4(5): 334-348.

[2]Whittaker J A, Thomason M Q. A Markov chain model for statistical software testing[J]. IEEE Transaction on Software Engineering, 1994, 20: 812-824.

[3]Wang Zai, Ke Tang, Xin Yao. Multi-objective approaches to optimal testing resource allocation in modular software systems[J]. IEEE Transactions on Reliability, 2010,59(3):563-75.

[4]Anand Saswat, Burke Edmund K. An orchestrated survey of methodologies for automated software test case generation[J]. Journal of Systems and Software,2013,86(8):1978-2001.

[5]秦强,胡昌振. 基于马尔科夫决策过程的软件测试与仿真[J]. 数值计算与计算机应用, 2014,35(2):92-102.

[6]Bao Xiao’an, Yao Lan. Adaptive software testing based on controlled Markov chain[J]. Jisuanji Yanjiu yu Fazhan/Computer Research and Development,2012,49(6):1332-1338.

[7]刘克. 实用马尔可夫决策过程[M]. 北京:清华大学出版社, 2004:3-15.

[8]Cai KY, Chen T.Y, Li Y. C., et al. Adaptive Testing of Software Components[J]. Proceedings of The 20thAnnual ACM Symposium on Applied Computing, Santa Fe, New Mexico, 2005: 1463-1469.

[9]Boer D P T, Kroese D P, Mannor S, Rubinstein R Y. A tutorial on the Cross-Entropy Method[J]. Annals of operations Research, 2005, 134(1): 19-67.

[10]Alon G, Kroese D P, Raviv T and Rubinstein R Y. Application of the Cross-Entropy Method to the Buffer Allocation Problem in a Simulation-Based Environment[J]. Annals of operations Research, 134:19-67.

[11]Rubinstein R Y. Cross-Entropy and Rara-Events for Maximal Cut and Bisect1ition Problems[C]. ACM Transactions on Modeling and Computer Simulation,27-53.[12]Margolin L. on the convergence of the cross-entropy method[J]. Annals of Operations Research, 2005,134(1):201-214.

[13]Harman M, Jones BF. Search-Based software engineering[J]. Information and Software Technology, 2001,43(14):833-839.

[14]Cai KY, Li YC, Ning YW. optimal software testing in the setting of controlled Markov chains[J]. European Journal of Operational Research, 2005,162(2):552-579.

Software Testing Strategy Based on Improved Markov Model

LI Ze-xue1, LI Xiang-min1, XUE Liang2

(1.Naval Aeronautical and Astronautical University, Yantai 264001;2.Naval Academy of Armament, Beijing 100161, China)

Abstract:A software testing method of optimizing testing strategy based on improved Markov model is presented in this paper. This method uses a new stochastic optimization method called Cross Entropy method. By iterative correcting of the testing profile in Markov model, we consider the minimization of testing cost and try to generate testing data automatically. The experimental results show that this optimization method is a promising option for tackling this problem. It can reduce the software testing cost effectively.

Key words:software testing; cross entropy method; rate of coverage

文章编号：1673-3819(2016)03-0108-05

收稿日期：2016-03-07

作者简介：李泽雪(1991-),男,河北秦皇岛人,硕士研究生,研究方向为控制理论及应用。 李相民(1965-),男,教授,博士生导师。

中图分类号:TP311.53

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.03.021

修回日期： 2016-03-14

薛亮(1976-),男,工程师。