改进的细菌觅食优化算法的性能研究
邹汪平
(池州职业技术学院信息技术系,安徽池州247000)
改进的细菌觅食优化算法的性能研究
邹汪平
(池州职业技术学院信息技术系,安徽池州247000)
摘 要:细菌觅食算法作为一种仿生计算方法,近年来大量学者对该种算法进行研究,改善算法的性能,但却无法同时兼顾算法寻优效率与精度,文中通过分析算法趋化操作中趋化步长对算法的影响,提出一种改进的趋化步长方法,加快算法收敛速度。对算法复制操作的研究,结合遗传算法中交叉变异思想,引入交叉因子与变异因子,改进算法精度,避免算法陷入局部最优。考虑两种改进方法的优势,受双种群遗传算法思想启发,提出改进的双菌群细菌觅食优化算法,通过实验验证算法的优越性。
关键词:细菌觅食算法;双菌群;交叉因子;变异因子;遗传算法;寻优性能
随着人类社会的发展进步,国防、交通、农业、金融等领域为了提高处理系统工作效率、合理利用现有资源,都在积极寻找各种优化方法、优化理论,将其应用到处理实际问题中,从而提高工作效率。然而在实际应用中通常会遇到方程数量多、维数高且具有非线性强的问题,因此,在处理现实优化问题过程中对优化算法提出了更高的要求。然而,现在普遍采用的一些优化算法在计算速度等方面往往难以满足要求。智能优化算法作为一种新型算法为处理复杂问题提供了可能性[1-16]。典型的智能优化算法包括遗传算法、蚁群优化算法、粒子群优化算法、人工鱼群优化算法、细菌觅食优化算法(BFO)等。其中细菌觅食优化算法作为一种基于群体的搜索技术,其性能相对于遗传算法更优秀,然而由于起步较晚,没有遗传算法成熟。随着人们逐渐认识到BFO算法的优点,该算法也成为学者们的热点研究对象。
当前,针对BFO算法的研究主要从参数改善和BFO算法与其他算法相融合两个方面进行。参数改善方面:Liu Y等通过对大肠杆菌相互作用机制的改进研究,初步研究分析了BFO算法的收敛性问题[3];Datta等则依据自适应增量调制原理设计了一种具有自适应趋化步长的细菌觅食优化算法[4];Chen等则提出了自适应协同菌群觅食优化算法[5]。在算法融合设计方面:Kim等通过将BFO算法与遗传算法相结合提出了GABFO算法[8-9];Chatterjee等将卡尔曼滤波器与BFO算法相结合,扩展了卡尔曼滤波解的质量[10];Tang等通过在细菌觅食优化算法中引入PSO算法基本思想,提出了快速细菌群算法[11]。
尽管大量学者对BFO算法进行了深入研究,然而由于该算法起步较晚,仍然存在着诸如精度不够高、收敛速度慢等问题[12-16],因此,本文通过对细菌觅食优化算法的优化机制进行分析,进而对趋化步长、复制操作详细分析,受双种群遗传算法启发提出了一种基于双菌群的改进细菌觅食优化算法,并通过试验测试对比,说明了该算法相对于传统细菌觅食算法的优势。
1 基于双菌群的改进细菌觅食优化算法
1.1算法趋化步长的改进
细菌觅食优化算法的趋化步长大小对细菌觅食寻优速度有直接影响,如果BFO算法采用大趋化步长则能够较迅速地找到最优解,然而同时会牺牲解的精度,增加算法复杂性,导致算法收敛速度过慢;反之,若趋化步长过小,则会导致寻优速度过慢的问题。因此,选择合适的趋化步长对算法的优化效果改善意义重大。以Rosenbrock函数为例,选取如表1所示测试参数,其中趋化步长λ分别选择0.001、0.005和0.01,以研究其对优化效果的影响。如图1所示为不同步长下Rosenbrock函数的优化曲线图,从图中可以看出当趋化步长为0.001时,其优化收敛速度较慢,且整个曲线呈较平缓的下降趋势,说明小步长的细菌觅食算法收敛速度较慢。而趋化步长为0.005和0.01时,优化曲线则出现了震荡现象,说明采用大步长的BFO算法寻优速率较快,然而却会出现震荡现象。
通过上述分析可以发现趋化步长的改进对算法的优化能够起到至关重要的作用,传统BFO算法菌群初始化一般按式(1)进行初始化操作。

式中:Xmax和Xmin分别为细菌觅食优化算法优化区间的最大值和最小值,X为细菌初始化位置。

表1 优化参数设置
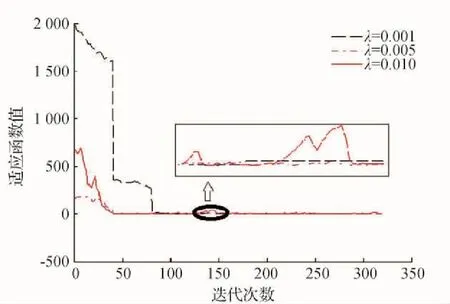
图1 不同趋化步长条件对BFO算法的影响
若种群规模S,P(I,j,k,l)为细菌i在优化空间内的一种可行解,表示细菌i在第j次趋向性操作、第k次复制操作以及第l次迁徙操作后的位置,则每次趋化操作后细菌的位置依式(2)、式(3)所示公式更新。

式中:C(i)为细菌i的趋化步长,φ(i,j)代表细菌i翻转时的单位随机向量,Δ(i)为任意产生的大小介于-1和1之间的单位随机方向向量。
通过对细菌菌群拥挤程度的分析,结合传统细菌觅食优化算法提出了一种根据平均粒子间距自适应改进的趋化步长思想。根据平均粒距思想定义细菌密度函数如下:

式中:S为菌群中细菌总数,L为细菌搜索空间的最长对角线长度,X(m,t)为序号为t的细菌在搜索空间第m维的坐标。 ̄X为当前搜索空间内第m维的所有细菌位置的平均坐标值。
当菌群中细菌数量较少时,即其密度较小时,可以通过较大趋化步长进行觅食优化,从而提高算法寻优效率;而当细菌数量多时,通过调小趋化步长从而提高寻优精度,因此,基于式(4)对传统细菌觅食算法中的趋化步长公式进行如下改进:

式中:Cmin≤C(t)≤Cmax,Dmin≤D(t)≤Dmax,Cmin为最小趋化步长,Cmax为最大趋化步长,且式(5)中A,B应满足

式中:Dmin为菌群中的细菌最小间距,Dmax为最大间距。
为验证改进趋化步长后的算法对传统细菌觅食算法在收敛性及精度方面的提高,采用表2所示参数对Rosenbrock函数进行测试,测试结果如图2所示,图中MBFO代表改进趋化步长后的细菌觅食优化算法,图中以点划线表示其优化曲线,从图2可以看出两种算法虽然都呈类似下降趋势,但改进步长后的算法在初期即开始快速收敛且不存在强烈震荡现象,相比传统细菌觅食优化算法有一定的改善。然而与传统BFO算法类似,仍然会出现局部最优现象,还需进一步研究。

表2 对比测试参数
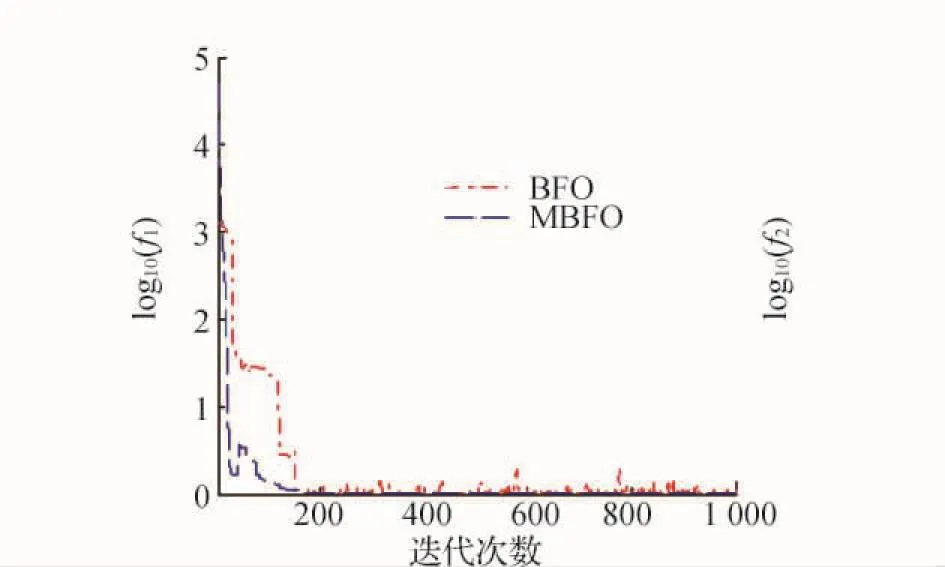
图2 改进趋化步长的Rosenbrock函数优化测试曲线对比
1.2复制操作的改进
传统细菌觅食优化算法中为使算法收敛速度更快,一般细菌在经过一定次数的迭代后,通过计算细菌的健康度函数,复制其中健康值较小的细菌而使其余细菌消亡。传统细菌算法中一般将某个趋化周期内的适应度函数之和作为衡量细菌觅食能力的依据。而实际上仅仅将单个周期内的适应度函数值作为判定依据可能会出现判断不准确的现象,导致精英细菌被误杀,同时也降低了菌群的菌种多样性。实际上,复制操作对BFO算法优化结果的影响主要在于选择策略与复制策略两方面。因此,要对其进行改进优化,则应从这两方面考虑:一方面应当考虑每个趋化周期内的最优细菌,并使其成为精英细菌,避免对其误杀;另一方面,引入遗传算法思想,对每个周期内适应度函数值好的细菌进行变异操作,同时采用交叉操作处理函数值交叉的细菌,从而增强菌群的细菌多样性,提高计算精度。
统计发现,细菌菌群中全局最优解与最优个体之间的亲和度相对于其他个体要强。因此,笔者推断与最优细菌有较大亲和度的细菌其适应函数值相对也应该较好。根据该思想,若能够使细菌觅食过程中能力较差个体不断向优秀个体学习,从而加快算法收敛速率,应能够对细菌觅食优化算法起到较大的改善作用。优化的最主要目标是在最短时间内获得搜寻目标最优值,而在细菌觅食算法复制操作中,实际起到积极引导作用的是最优细菌,结合遗传算法思想,设计一种杂交算子引导较差细菌向优秀细菌学习,从而改善算法当前的不利状态,同时定义变异算子使其能够在当前优质细菌附近产生小扰动,避免细菌停滞不前,防止算法陷入局部最优。定义杂交算子与变异算子分别如式(3)、式(4)所示。
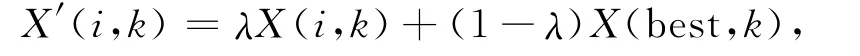

式中:λ为介于0~1的均布随机数,X(best,k)为k时刻菌群最优位置。通过改进的复制操作使当前优秀细菌与最差细菌个体杂交,并充分结合当前已获得的信息,使最差细菌逐渐向最好位置靠近,从而使算法收敛速度大大提高。
为了验证引入变异算子和杂交算子的改进复制操作的细菌觅食优化算法的优势性,仍然以Rosenbrock函数为测试函数,采用相同的参数,优化结果如图3所示,从图中可以明显看出,传统的细菌觅食算法在1 000代左右陷入了局部最优,而改进复制操作的细菌优化算法则避免出现局部最优现象,同时改进后的算法解的精度与传统BFO算法相比更高,然而算法的收敛速度及其稳定性也有所降低。这说明改进复制操作的细菌优化算法能够使得适应度函数值差的细菌不断向优质细菌学习,同时在学习过程中有目的性地对其搜索区域进行搜索,提升细菌搜索全局最优解的能力,提高算法解的精确性,避免算法的早熟,使得算法的稳定性和收敛速度降低,但算法更加复杂,因此,还需进一步研究。

图3 改进复制操作的Rosenbrock函数优化测试曲线对比
2 双菌群在细菌觅食算法中的应用
通过研究表明大肠杆菌在觅食过程中,其菌群之间保持特有的信息交换机制,通过菌群间信息交换提高对周围环境的了解。在遗传算法的改进研究中,有学者提出了双种群遗传算法得到了相对较好的优化效果。基于本文前述分析,改进趋化步长的算法其局部搜索能力较强,在不同细菌密度情况下,趋化步长会自适应发生变化,在密度较大区域,趋化步长会自适应地减小,以便提高解的精度,然而却容易导致算法陷入局部最优;而改进的复制操作细菌觅食算法,能够有利于陷入局部最优的细菌个体摆脱局部最优,同时使得适应函数较差的细菌向优质细菌学习,增强细菌多样性,提高算法解的精度,然而却会牺牲算法稳定性和收敛速度。两种改进算法优劣势恰好互补,因此,依据双菌群思想,本文提出采用两个菌群进行算法优化,其中一个菌群采用改进的趋化步长细菌觅食算法,重点改进算法局部搜索能力,另一个菌群采用改进复制操作的细菌觅食算法,重点改善菌群全局优化能力,并提高优化算法解的精确性。同时在两个菌群间建立联系机制,即在每次复制操作完成后,将菌群中优质细菌与另一菌群最差细菌进行交换,从而实现菌群相互学习的功能,促进算法收敛。鉴于细菌优化算法实际上是对自然菌群觅食机制的模拟,极有可能存在生物界常见的黄金分割点现象,因此,最优细菌与最差细菌数量选择比例上宜采用黄金分割率。
为验证双菌群思想在细菌觅食算法中的应用,采用表3所示参数Rosenbrock函数进行优化测试。测试中对测试函数独立计算50次,并将统计结果进行对比,如表4所示。其中:f1代表被测试函数,DFBFO代表双菌群细菌觅食算法,从表中可以看出,采用BFO算法,函数f1比较容易陷入局部最优值,而DFBFO算法则明显地跳出了局部最优值,且从解的精度角度考虑,DFBFO算法所求得的最优解与函数全局最优解更接近,而从表中也注意到采用DFBFO算法,由于细菌多样性提高了,因此,最终的平均值和最优值差别较大。说明本文所提出的双菌群细菌觅食算法能够取得较好的效果。

表3 优化参数设置
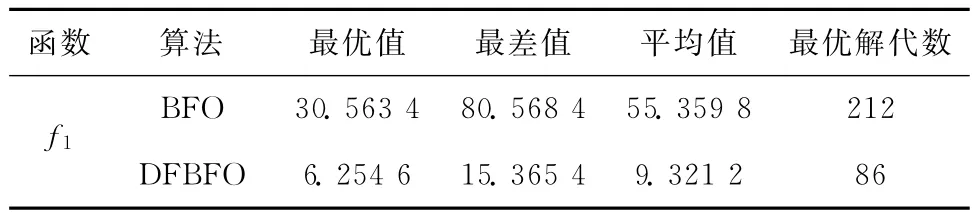
表4 优化结果对比
3 结束语
本文主要对细菌觅食优化算法进行了研究,详细分析了趋化步长、复制操作对算法的影响。根据平均粒距思想定义了细菌密度函数,改进了趋化步长,提高了细菌觅食算法的局部搜索能力和收敛速度。受遗传算法中交叉变异思想启发,在细菌复制操作中引入了变异因子与交叉因子,通过实验验证,发现改进后的算法提高了解的精确性,同时也增加了细菌多样性。然而实验验证,上述改进仍存在各自缺点,受双种群遗传算法启发,提出了两种改进算法相结合的双菌群觅食优化算法,使两种改进算法优势互补,提高了解的精度,同时也使算法跳出了局部最优,与传统细菌觅食算法相比取得较好的优化效果。
参考文献
[1] 胡洁.细菌觅食优化算法的改进及应用研究[D].武汉:武汉理工大学,2012.
[2] 周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,20:16-21.
[3] LIU Y,PASSINO K M,POLYCARPOU M M.Stability analysis of m-dimensional asynchronous swarms with a fixed communication topology[J].Automatic Control,IEEE Transactions on,2003,48(1):76-95.
[4] DATTA T,MISRA I S,MANGARAJ B B,et al. Improved adaptive bacteria foraging algorithm in optimization of antenna array for faster convergence[J]. Progress In Electromagnetics Research C,2008,1:143-157.
[5] CHEN H,ZHU Y,HU K.Self-adaptation in bacterial foraging optimization algorithm[C]//Intelligent System and Knowledge Engineering,2008.ISKE 2008. 3rd International Conference on.IEEE,2008,1:1026-1031.
[6] 刘小龙,赵奎领.基于免疫算法的细菌觅食优化算法[J].计算机应用,2012(3):634-637,653.
[7] 姜建国,周佳薇,郑迎春,等.一种自适应细菌觅食优化算法[J].西安电子科技大学学报,2015(1):75-81.
[8] KIM D H,ABRAHAM A,CHO J H.A hybrid genetic algorithm and bacterial foraging approach for global optimization[J].Information Sciences,2007,177(18):3918-3937.
[9] KIM D H,CHO J H.A biologically inspired intelligent PID controller tuning for AVR systems[J].International Journal of Control Automation and Systems,2006,4(5):624-636.
[10]CHATTERJEE A,MATSUNO F.Bacterial foraging techniques for solving EKFBased SLAM problems [C]//Proc.Int.Control Conf.2006.
[11]TANG W J,WU Q H,SAUNDERS J R.A bacterial swarming algorithm for global optimization[C]//Evolutionary Computation,2007.CEC 2007.IEEE Congress on.IEEE,2007:1207-1212.
[12]李珺,党建武,卜锋.细菌觅食优化算法的研究与改进[J].计算机仿真,2013(4):344-347,415.
[13]李娜,雷秀娟.细菌觅食优化算法的研究进展[J].计算机技术与发展,2014(8):39-44.
[14]张荣沂.一种新的集群优化方法——粒子群优化算法[J].黑龙江工程学院学报(自然科学版),2004(4):34-36,62.
[15]孟洋,田雨波.细菌觅食优化算法的边界条件[J].计算机应用,2015(S2):111-113,154.
[16]李珺,党建武.细菌觅食算法求解高维优化问题[J].计算机应用研究,2016(4):1-6.
[责任编辑:郝丽英]
On the performance of improved bacterial foraging optimization algorithm
ZOU Wangping
(Department of Information Technology,Chizhou Vocational and Technical College,Chizhou 247000,China)
Abstract:As a kind of bionic computing method,bacterial foraging optimization algorithm is studied and analyzed by a large number of scholars in order to improve its performance.But scholars can't take into account the efficiency and precision of the algorithm.This paper,analyzes the effect of the step size on the algorithm in the chemotaxis operation of algorithm,proposes a method of improved chemotaxis step,and accelerates the convergence rate of the algorithm.The research on algorithm replication operation,combining the crossover and mutation theory of genetic algorithm,introduces variation factor and interleave factor,which will enhance the precision of the algorithm and avoid the algorithm into a local optimal solution.Considering the advantages of the two methods,inspired by the idea of double population genetic algorithm,this paper puts forward an improved bacterial foraging optimization algorithm.The experimental results prove the superiority of the algorithm.
Key words:bacterial foraging algorithm;double bacteria group;interleave factor;variation factor;genetic algorithm;optimization performance
中图分类号:TP3
文献标识码:A
文章编号:1671-4679(2016)02-0029-05
收稿日期:2016-02-24
基金项目:安徽省2016年高校优秀青年人才支持计划重点项目(gxyqZD201653);安徽省2015年度省级质量工程项目(2015gxk113);安徽省2014年度省级质量工程项目(2014jyxm524);安徽省2013年度省级质量工程项目(2013jxtd065)
作者简介:邹汪平(1982-),男,副教授,研究方向:智能算法应用.

