一种改进的分布式多维定标算法的研究

邬春明，宋强欢，杨　涛

(东北电力大学 信息工程学院，吉林 吉林 132012)

一种改进的分布式多维定标算法的研究

邬春明，宋强欢，杨涛

(东北电力大学 信息工程学院，吉林 吉林 132012)

摘要:无线传感器网络中节点间通信容易受到环境因素和传输衰减因素等的影响，从而造成节点的定位不准确。为减小节点定位误差，在分布式多维定标算法基础上提出了改进的WMDS-MAP(P)算法。采用加权算法求出每个锚节点的环境影响参数和传输衰减参数对，并在构建局部空间的节点矩阵时考虑这两个因素；采用最小二乘算法选出锚节点中最优的环境影响参数和传输衰减参数对，从而使节点间的一跳距离估计值更逼近真实值。仿真结果显示改进的算法相对于经典的MDS-MAP(P)算法节点平均定位误差减少了17%左右，可以有效提高节点的定位精度。

关键词:分布式多维定标;WMDS-MAP(P)算法;加权算法;最小二乘算法

无线传感器网络具有自组网、低功耗及低成本的优点，目前广泛用于智能交通、目标跟踪、森林防火及军事领域等。在这些运用中节点的定位显得尤为重要，目前，节点定位技术的研究得到了科研工作者的广泛关注，并且也取得了丰富的成果。无线传感器网络的节点定位算法大致可以分为两大类：一种是基于测距的定位算法，例如：RSSI(singal received strength)、TOA(Time of Arrival)、AOA(Angle of Arrival)、Cooperative ranging、COLA(Complexity-reached 3D trilateration localization approach)[1-5]等。另一种是基于非测距算法，例如：DV-HOP、MCL(Monte Carlo Localization)、CDL(Color-Theory-Based Dynamic Localization)、WMCL(Weighted Monte Carlo Localization)[6-9]等。无线传感器网络中，节点定位的精度很大依靠于节点的测距精度，而由于节点与节点之间的通信过程容易受到复杂环境因素、多路径损耗及传输路径损耗等影响，使得节点间的定位误差较大。如今，考虑这些因素的定位算法已经取得了较高的定位精度，如李建坡等提出的基于RSSI值节点不规则传播模型的三维定位算法[10]、姚国提出基于RSSI值的独立目标的定位和跟踪的锐利指数模型[11]。

2003年，密苏里哥伦比亚大学的Yi Shang等人将多维标度(multidimensional scaling， MDS)的数据分析方法应用于无线传感器网络节点定位，提出了MDS-MAP算法(multidimensional scaling map algorithm)[12]，基于多维标度的定位算法是根据数据之间的相异性关系进行定位，其可以分为度量多维标度技术(metric MDS)和非度量多维标度技术(nonmetric MDS)，由于其具有矩阵维数大、计算复杂度高及不适合大规模不规则的无线传感器网络(WSN)的缺点，研究者提出了MDS-MAP(P)分布式局部定位算法[13-14]，它能够获得较好的定位精度，其定位精度也很大程度上取决于局部空间距离矩阵D中的距离值与真实值之间误差的大小。本文在MDS-MAP(P)算法基础上提出了WMDS-MAP(P)算法(Weighted multidimensional scaling map algorithm)，其在构建局部空间的距离矩阵D时采用加权算法和最小二乘算法相结合使矩阵中距离值更加接近于真实值，再使用经典的MDS-MAP(P)算法，从而获得较好的定位精度。

1MDS-MAP(P)算法的介绍

MDS-MAP(P)是在MDS-MAP的基础上改进而来，其能够克服MDS-MAP中矩阵维数大、计算复杂度高及不适合大规模不规则的无线传感器网络(WSN)的缺点。采用基于MDS的分布式局部定位算法，充分利用网络中任一节点的连通信息构建该节点的局部相对坐标图，再通过一定的拼接策略将所有的局部相对坐标图拼接成全局相对坐标图，最后通过一定的坐标转换方法将相对坐标转换成绝对坐标，具体步骤如下：

阶段1：在无线传感器网络中采用洪泛的方法使网络中的每个节点只与距其两跳通信半径范围内的节点进行通信并收集其ID及节点间距离信息，采用一定的划分策略将网络中每个节点划分为一个局部空间，即若无线传感器网络中分布着N个节点，则将该区域划分为N个局部空间。

阶段2：对于网络中任一节点构建距其两跳范围内的节点间距离矩阵D，对处于距其一跳距离的邻居节点采用的是基于RSSI(信号接收强度值)测距方法计算其距离值，而对于非邻居节点的两跳节点，采用Eucilidean与最小路径相结合的方法计算其距离值。

阶段3：当完成每个节点的局部划分及求出局部的距离矩阵D后采用经典的MDS方法计算各局部空间的相对坐标。

阶段4：当网络中所有的局部空间的相对坐标均求出时，在所有的局部相对坐标图中挑选出连通度最高、节点数量最多的局部相对坐标图作为主坐标图，并将与主坐标图具有公共节点最多的局部相对坐标图作为拼接对象，按此原则依次进行拼接直至形成全局相对坐标图。

阶段5：根据锚节点在全局相对坐标图中相对坐标与绝对坐标之间的转换关系，将网络中所有节点的相对坐标转换成绝对坐标。

2改进的WMDS-MAP(P)算法

在构建局部空间的距离矩阵D时，距离矩阵D′与真实距离矩阵D误差大小将决定最终节点的定位精度的高低，在经典的MDS-MAP(P)算法中，在计算节点的一跳距离时采用的是基于RSSI的测距方法，由于节点与节点之间通信时接收到RSSI值容易受到外界环境和信号传输衰减损耗的影响，从而造成定位误差较大。本文将充分考虑这两个参数的影响，通过改进MDS-MAP(P)算法提出WMDS-MAP(P)算法，即分别通过计算出环境影响参数和信号传输衰减参数，在构建局部空间节点间的距离矩阵时考虑这两个因素，并通过加权算法和最小二乘算法进行优化，从而使得一跳距离估计值更逼近真实值，从而获取一个较好的定位精度，具体改进步骤如2.1小节和2.2小节所示。

信号衰减模型为

(1)

式中：RSS(d)为锚节点与未知节点之间的距离为d时信号接收强度值，单位为dBm；RSS(d0)为通信距离为d0时信号接收强度值；d0为参考值，取值为1 m；δτ为服从(0，δ2)高斯分布的噪声随机变量。

将式(1)进行简化得

(2)

其中。

S=RSS(d0aa)[dBm]-δτ

(3)

假设锚节点n1，坐标为(x,y)，周围有3个一跳距离的锚节点n2,n3,n4，其坐标分别为(x1,y1),(x2,y2),(x3,y3)，并距节点n1分别为d1,d2,d3。其分布如图1所示。

图1　锚节点分布图

则根据式(2)、(3)可得

(4)

节点n1与节点n2,n3可得

(5)

由式(5)可得

(6)

2.1锚节点参数对的加权算法

由节点n1与节点n2,n3可以得到环境影响参数λ1和信号传输衰减参数S1，相应地，节点n1与节点n2,n4、节点n3,n4可得到环境影响参数和信号传输衰减参数λ2、S2和λ3、S3。

则通过加权可得

(7)

(8)

(9)

(10)

通过上述算法可知，无线传感器网络中任一锚节点都能得到一个特定的环境影响参数和信号传输衰减参数，并将其值保存起来。由于局部空间计算的节点间距离估计值与真实值之间有误差，利用胁强系数来表示估计值与真实值之间的接近程度，其定义为

STRESS=∑(d^ij-dij)2

(11)

式中：d^ij为通过测量得到的节点间距离值；dij为空间内节点的估计位置的距离值。

2.2采用最小二乘算法优化参数对

在局部空间内每个锚节点都保存着由上述算法计算出的一对环境影响参数和信号传输衰减参数(S,λ)，采用最小二乘算法从这些锚节点中选出使胁强系数最小的环境影响参数和信号传输衰减参数。

(12)

则最小胁强系数为

(13)

式中：dij为空间内估计位置的距离值。式(13)是一个最小二乘算法问题，其是根据局部空间中锚节点的环境影响参数和信号传输衰减参数对的解空间进行穷举来搜索求解，通过式(13)可以得到最优的环境影响参数和信号传输衰减参数对(Sp,λp)，未知节点保存(Sp,λp)，并在后续计算节点距离时采用其进行计算。

当局部空间内任一节点与其邻居节点进行通信时，节点接收到来自邻居节点的RSSI值，并考虑上述计算出的最优环境影响参数和信号传输衰减参数对(Sp,λp)，从而计算出一跳节点的距离。采用的上述的WMDS-MAP(P)计算出一跳节点间的距离，同时在计算二跳节点距离时采用二跳距离采用的是Eucilidean与最小路径相结合的方法，从而构建出局部空间的节点距离矩阵D′。

3实验结果与分析

实验部分采用的是MATLAB7.0软件对改进的WMDS-MAP(P)算法进行仿真验证，并且对MDS-MAP算法、MDS-MAP(P)算法分别进行仿真，根据得到的仿真结果进行对比分析，从而对改进算法的性能进行分析。

3.1仿真环境与参数设置

本文的仿真环境是在一个200m×200m的正方形区域内，区域内随机分布着200个节点，其中锚节点是随机选取，各个节点设置的通信半径相同，重复仿真实验500次，并将其实验结果的平均值作为最终的实验结果。

实验结果采用平均定位误差进行衡量算法的性能指标，平均定位误差为

(14)

归一化误差为

(15)

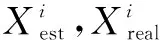
3.2算法的性能分析

图2a和图2b为通信半径分别为20 m和25 m，高斯噪声的方差δ为2时，节点的平均定位误差随锚节点数量变化的曲线，从图中可以看出：通信半径相同时，随着锚节点数量的增加，与经典的MDS-MAP算法和MDS-MAP(P)算法相比，改进的WMDS-MAP(P)算法的平均定位误差分别降低了32%和17%左右。

a　通信半径R=20 m，高斯噪声方差δ=2

b　通信半径R=25 m，高斯噪声方差δ=2

图3a和图3b为锚节点分别是8和10，δ为2时，节点的平均定位误差随网络的连通度变化的曲线关系图。从图中可以看出随着连通度的提高，节点的平均定位误差逐渐减小，当连通度为20以上时，节点的平均定位误差基本不变，这是因为连通度越高，在计算二跳距离时，最小路径更接近真实值，从而获得更好的定位精度。

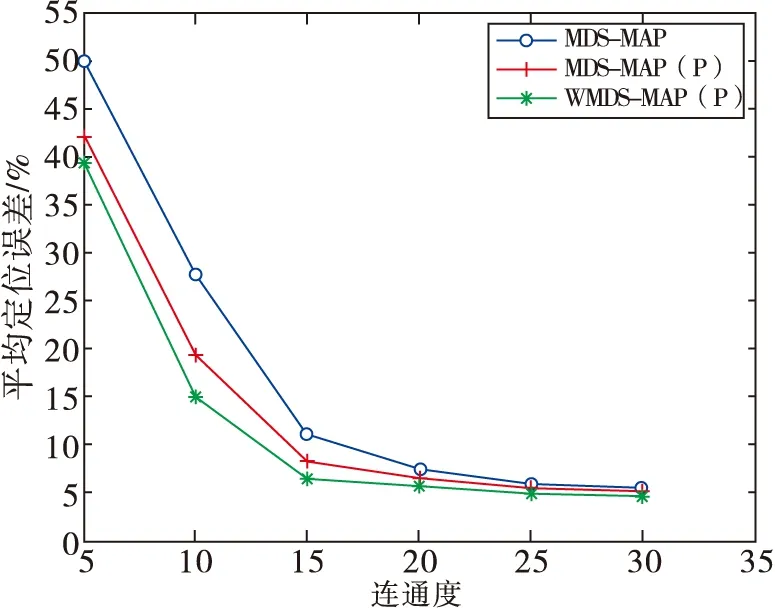
a 锚节点数量M=8，高斯噪声方差δ=2

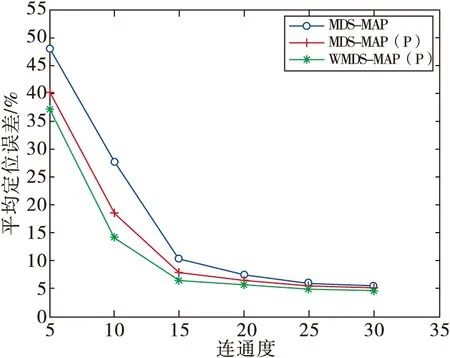
b 锚节点数量M=10，高斯噪声方差δ=2

4总结

在真实环境下，节点间通信容易受到环境因素和传输衰减因素的影响，因此，在MDS-MAP(P)算法的基础上提出了WMDS-MAP(P)算法，从仿真结果中可以看出改进的算法能够克服复杂环境的影响，且平均定位误差降低17%左右。将该算法的改进部分用于其他基于MDS-MAP(P)改进算法中，可以提高一定的节点定位精度。未来工作是将考虑无线传感器网络区域为不规则区域时，该改进算法是否依然能够获得较好的定位精度。同时，考虑在改进算法的基础上减少在局部相对坐标转换为全局绝对坐标时产生的误差，从而实现更高的定位精度。

参考文献：

[1]ABID M A, CHERKAOUI S. 3D compressive sensing for nodes localization in WNs based on RSS[C]//Proc. IEEE International Conference on Communications. Beijing：IEEE Press，2012：5195-5199.

[2]KAUNE R. Accuracy studies for TDOA and TOA localization[C]//Proc. 15th International Conference on Information Fusion. Singapore：IEEE Press，2012:408-415.

[3]HARA S, ANZAI D, YABU T. A perturbation analysis on the performance of TOA and TDOA localization in mixed LOS/NLOS environments[J]. IEEE transactions on communications, 2013,61(2):679-689.

[4]SAVARESE C, RAVAEY J M, BEUTEL J. Location in distributed ad-hoc wireless sensor networks[C]//Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing. Salt Lake City：IEEE Press，2001: 2037-2040.

[5]SHIH C Y, MARRON P J. COLA: complexity reduced trilateration approach for 3D localization in wireless sensor networks[C]//Proc. 4th International Conference on Sensor Technologies and Applications. Venice：IEEE Press, 2010:24-32.

[6]NICULESCU D, NATH B. Ad Hoc positioning system (APS) [C]//Proc. IEEE Global Telecommunications Conference. San Antonio：IEEE Press，2001: 2926-2931.

[7]HU L X, EVANS D. Localization for mobile sensor networks[C]//Proc. 10th Annual International Conference on Mobile Computing and Networking. Philadelphia：IEEE Press，2004:45-57.

[8]CHANG T, WANG K, HSIEH Y L. Color-theory-based dynamic localization in mobile wireless sensor networks[C]//Proc. 1st Workshop on Wireless Ad Hoc Sensor Networks. London：IEEE Press，2005: 73-78.

[9]ZHANG S G，CAO J N，CHEN L J. Accurate and energy-efficient range-free localization for mobile sensor networks[J]. IEEE transactions on mobile computing, 2010,6(9):897-910.

[10]LI J P, ZHONG X X, LU I T. Three-dimensional node localization algorithm for WSN basd on diferential RSS irregular transmission model[J]. Journal of communications,2014,5(9):391-397.

[11]GAO Y, HUANG K D, JIANG N Y. An exponential Rayleigh model for RSS-based device-free localization and tracking[J]. IEEE transactions on mobile computing，2015,3(15):484-494.

[12]SHANG Y, RUML W, ZHANG Y, et al. Localization from mere connectivity[C]//Proc. 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing. New York：IEEE Press，2003: 201-212.

[13]SHANG Y，RUML W. Improved MDS-based localization[J]. Twenty-third annual joint conference of the IEEE computer and communications societies，2004(4)：2640-2651.

[14]刘春平. 基于多维尺度分析的三维非均匀无线传感网定位算法研究[D].杭州：杭州电子科技大学，2014.

邬春明(1966— )，硕士，教授，硕士生导师，从事无线通信技术领域科学研究与教学工作；

宋强欢(1992— )，硕士生，主要从事无线传感网络定位；

杨涛(1991— )，硕士生，主要从事无线传感网络定位及系统硬件设计的研究。

责任编辑：薛京

Study of improved MDS-MAP (P) algorithm

WU Chunming，SONG Qianghuan, YANG Tao

(InformationEngineeringCollege,NortheastDianliUniversity，JilinJilin132012,China)

Abstract:the nodes position precision is vulnerable to the environmental factors and the influence of transmission attenuation factors in wireless sensor networks. To reduce the node positioning error, a WMDS-MAP(P) algorithm based on the distributed multi-dimensional scaling map(MDS-MAP(P)) algorithm is proposed. Using the weighted algorithm find out the environmental impact parameters and the parameters of transmission attenuation of each anchor node. And consider the two factors in computing the local space node matrix. Using the least squares algorithm to select the anchor nodes the most optimal environmental impact parameters and the parameters of transmission attenuation, and make one-jump estimate distance more close to the real value. Compared with the classical MDS-node MAP(P) algorithm, the simulation results show that the improved algorithm can reduce the average position error is about 17%, and it can effectively improve the nodes positioning precision.

Key words:multidimensional scaling map algorithm; weighted multidimensional scaling map algorithm; weighted algorithm ; the least squares algorithm

中图分类号:TN92

文献标志码：A

DOI：10.16280/j.videoe.2016.03.021

基金项目：国家自然科学基金项目(61301257)；吉林省科技发展计划资助项目(2013020605GX);吉林省教育厅“十二五”科学技术研究项目(吉教科合字[2015]第250号)

作者简介：

收稿日期：2015-07-18

文献引用格式：邬春明，宋强欢，杨涛.一种改进的分布式多维定标算法的研究[J].电视技术,2016，40(3)：98-102.

WU Chunming，SONG Qianghuan, YANG Tao.Study of improved MDS-MAP (P) algorithm[J].Video engineering,2016,40(3)：98-102.