基于结构元素分解的二值形态学并行快速算法

程　楷，程　勇

(1.上海交通大学　图像通信与信息处理研究所，上海　200240；2.南京工程学院　通信工程学院，江苏　南京　211167)

基于结构元素分解的二值形态学并行快速算法

程楷1，程勇2

(1.上海交通大学图像通信与信息处理研究所，上海200240；2.南京工程学院通信工程学院，江苏南京211167)

摘要:提出结构元素为4连通或8连通区域时数学形态学膨胀腐蚀的快速算法。首先将二维结构元素分解成不同方向的一维结构元素；然后，通过分步移位位操作实现二维形态学膨胀、腐蚀算法；最后利用二值图像的特点，将连续的若干个像素点视为一个整体并行操作，从而实现算法性能提升，相比于其他算法具有速度快、易操作等优点。

关键词:分解；并行；膨胀；腐蚀

1数学形态学处理

数学形态学用具有一定形态的结构元素去量度和提取图像中的对应形状，从而实现对图像的分析和识别。数学形态学处理在边缘检测、特征提取、图像分割、细节去除、孔洞填充等图像处理以及计算机视觉领域有着非常广泛的应用[1]。

形态学处理一般算法是将一个结构元素在二值图像上逐点移动，对每个像素点进行若干次逻辑判断从而得到处理结果。为提高形态学处理的运算效率，杨琨等提出利用结构元素在运算过程中存在的大量的重复运算区域，通过在后一次运算中使用前一次运算的结果来缩短运算时间的算法[2]。该算法具有理论基础简单，实现方便的特点，但是对于比较小的结构元素，性能提高不明显。陆宗琪等提出采用线段编码的方式，将当前线段与其相邻的上下线段之间进行逻辑运算，从而实现膨胀腐蚀运算[3]。该算法由于需要对二值图像进行额外的线段编码工作，导致对单个膨胀腐蚀操作效果的改善大打折扣，没有较为广泛的适用性。Cheng等通过检测二值图像的边缘，对边缘像素点进行操作来实现膨胀腐蚀的快速运算[4]，对于边界比较复杂的情况，该算法的优化效果不好。MatthewJ.Thurley等利用图形处理器(GPU)的并行计算优势，采用CUDA这一NVIDIA推出的并行计算架构进行性能优化[5]。该算法对于分辨率较高的图像会有较高的性能提升，但是对硬件的要求较高，适用性不强。

本文将4连通或8连通结构元素分解为不同方向上的一维结构元素，利用分步的移位操作实现形态学腐蚀膨胀。同时利用二值图像的特点，即其像素值为0或者1，采用分段的方式，将相邻的若干个像素看成一个整体，通过并行操作实现算法性能提升。算法的速度可以提高4～6倍，具有易操作适用性广泛的特点。

2膨胀与腐蚀

定义1，作为Z2中的集合A和B，B对A的膨胀定义为

A⊕B={Z|(B^Z∩A≠Φ)}

(1)

该公式可以等价表示为

A⊕B={Z|(B^Z∩A⊆A)}

(2)

式中：z表示结构元素的位移；B^表示集合B的反射集合。由定义得出的膨胀算法为将给定的结构元素在二值图像上依次平移，若该结构元素覆盖的原二值图像上有一个或多个点像素值为1，则将结构元素中心点所在的二值图像像素值赋为1，否则将该点像素值赋为0，当结构元素走完整幅图像时，便可以得到膨胀结果。

定义2，作为Z2中的集合A和B， B对A的腐蚀定义为

A⊖B={Z|(B)Z⊆A}

(3)

该公式可以等价表示为

A⊖B={Z|(B)Z∩Ac=Φ}

(4)

式中：Ac是A的补集；Ф是空集。

同理，由定义得出的腐蚀算法为当结构元素覆盖的二值图像像素值全部为1时，将结构元素中心点所在的二值图像像素值赋为1，否则赋为0。由定义得出的形态学处理算法效率较为低下，原因在于需要遍历整个图像的每个像素值，对于每个像素值，仍需要进行一系列的逻辑判断才能得到运算结果。当结构元素较为庞大或者二值图像分辨率较高时，处理速度会变得尤其慢。此外，由于结构元素在二值图像上依次滑动处理每个像素，因而会有大量重复的逻辑判断，当图像前景区域比较大时，这些重复判断会造成更加多的资源浪费。

结论1，由定义可知膨胀和腐蚀关于集合求补运算和反射运算是对偶的，即

(A⊖B)c=Ac⊕B^

(5)

(A⊕B)c=Ac⊖B^

(6)

因此，可以利用相同的结构元素，使用B膨胀图像的背景(即膨胀Ac)，并将结果求补即可得到B对该图像的腐蚀结果。

3基于分解的膨胀腐蚀快速算法

3.1基于分解的膨胀快速算法

3.1.1算法原理

对于一幅需要进行形态学操作的二值图像，不需要对每个像素进行单独处理，而是可以利用一个无符号整数(unsignedint)来表示连续的若干个像素值，这个无符号整数的每一位均代表原图中的一个像素点的像素值。因此，一幅M×N的二值图像可以按行表示为M个整数，其中每个整数都是一个N位的无符号整数。同理，也可以按列表示为N个整数，其中每个整数都是一个M位无符号整数。

本文将讨论4连通和8连通的结构元素，如图1所示。

图1结构元素

对于4连通的结构元素，可以将其分解为(1 1 1)和(1 1 1)’两个方向上的一维结构元素，其中(1 1 1)’表示矩阵(1 1 1)的转置。(1 1 1)对原始图像的膨胀结果可以表示为将图像中每个像素值为1的点的左、右像素点均赋值为1，这一步也可以通过将按行构造出的若干个整数向左按位平移一位，向右按位平移一位，将这3个整数按位取或得到。(1 1 1)’对原始图像的膨胀结果可以表示为将图像中每个像素值为1的点的下、上像素点均赋值为1，这一步也可以通过将按列构造出的若干个整数向左按位平移一位，向右按位平移一位，将这3个整数按位取或得到。最后，将上述两个步骤得到的两个整数按位取或即可得到最终膨胀结果。4连通膨胀算法流程见图2所示。

图24连通膨胀算法流程

对于8连通的结构元素，同样可以将其分解为(1 1 1)和(1 1 1)’两个方向上的一维结构元素。(1 1 1)对原始图像的膨胀结构可以表示为将图像中每个像素值为1的点的左、右像素点均赋值为1，这一步也可以通过将按行构造出的若干个整数向左按位平移一位，向右按位平移一位，将这3个整数按位取或得到。(1 1 1)’对原始图像的膨胀结构可以表示为将图像中每个像素值为1的点的下、上像素点均赋值为1，与4连通结构元素不同的是，这一步需要将(1 1 1)对原始图像膨胀的结果按列构造出的若干个整数向左按位平移一位，向右按位平移一位，将这3个整数按位取或得到。8连通膨胀算法流程见图3所示。

图38连通膨胀算法流程

3.1.2算法流程

根据上述原理，可以通过对按行或者按列构造的若干个整数进行位操作来得到最终膨胀结果。将若干个相邻像素点视为一个整体使用并行的操作方式可以提升算法的效率。

在本文中，对于一幅大小为M×N的二值图像，将每一行连续的32个像素值作为一个整数，当N/32不等于0时，即每行像素值个数不是32的整数倍时，在每行末尾补充32-N%32个值为0的像素，这样便可以将原始的M×N的二值图像分段成一幅M×⎣N%32」的新图，该图中每个“像素值”均为一个32位的无符号整数。构造过程如图4所示，图5显示了构造之前的图像和对应分段图。

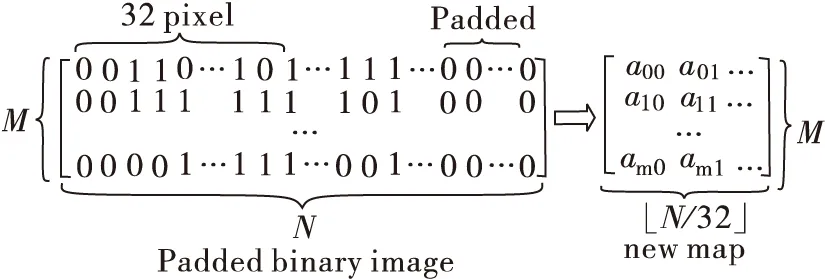
图4　分段图构造过程

同理，若将原始图像矩阵转置后进行如上操作，可以得到图像按列构造出的分段图。 构造完二值图像对应的分段图之后，形态学膨胀腐蚀便可以在分段图上进行操作。4连通和8连通的膨胀快速算法见图6和图7。在进行移位操作时，需要考虑相邻两个整数的边界位，即当x的最后一位为1，而x右边的整数y第一位为0时，若需要进行右移移位，则需要将y的第一位置为1；同理，当x的第一位为1，而x左边的整数z最后一位为0时，若需要进行左移移位，则需要将z的最后一位置为1。

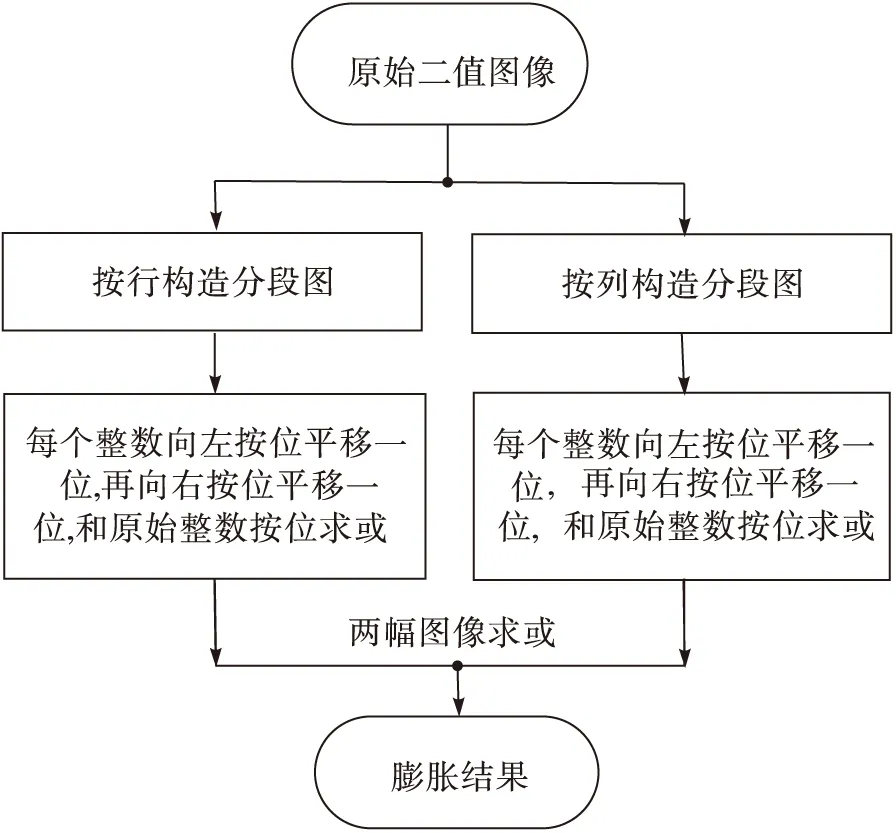
图6　4连通膨胀快速算法

3.2基于分解的腐蚀快速算法

根据结论1，可以知道形态学腐蚀和膨胀具有对偶性的特点，因此为得到4连通或者8连通结构元素对一幅二值图像的腐蚀结果，将二值图像取反，然后进行上述膨胀操作，最后将得到的结果再次取反即可。由于二值图像取反操作也可以在分段图上进行，因此腐蚀快速算法的流程仍是建立在分段图之上的。

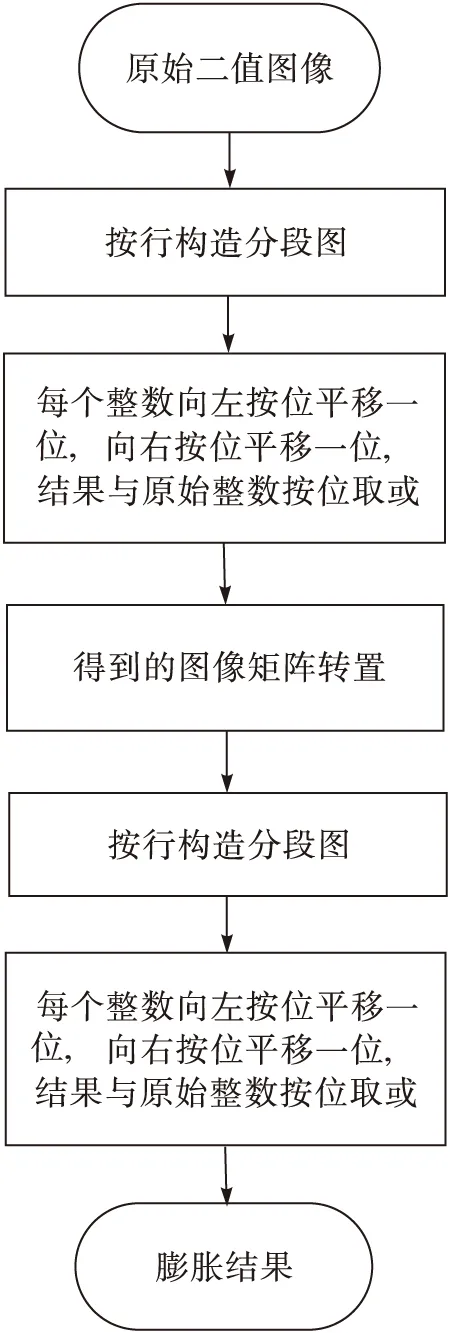
图7　8连通膨胀快速算法

3.3性能比较

在IntelCorei5-3470CPU@ 3.2GHz，4GbyteRAM，Windows8 32位操作系统的硬件环境下进行实验。对不同分辨率以及不同纹理复杂度的二值图像进行了实验，采用的结构元素为8连通结构元素，进行膨胀实验的原始图像以及最后结果见图8，性能比较见表1。由于运行时间与计算机速度、负载有关，因此本文中的数据取的是平均值。由于本文的快速算法只是对32bit整数操作，并不关心整数的具体内容，因此二值图像的纹理复杂程度并不会对本算法的性能有较大影响。

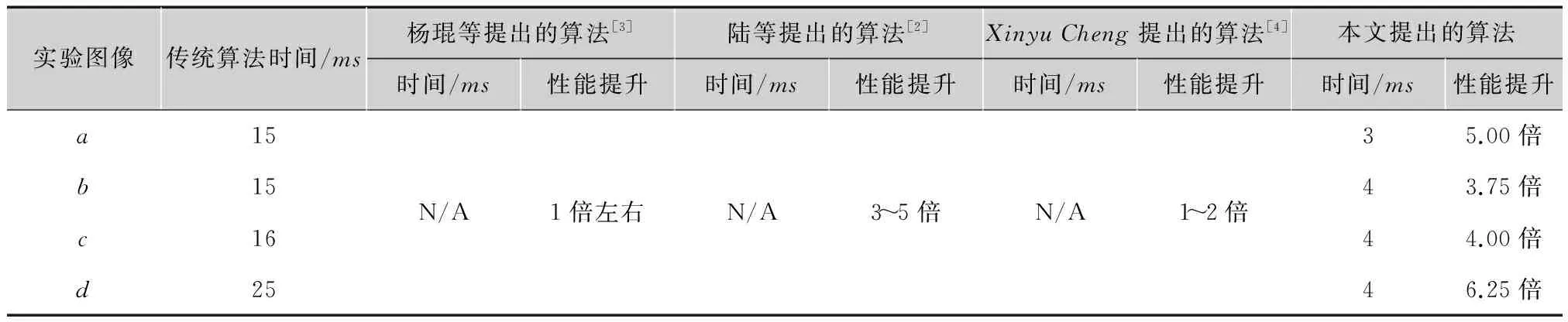
表1　性能比较

4结论

本文提出了一种基于结构元素分解的二值形态学并行快速算法。将结构元素分解为不同方向的一维结构元素，通过分步的移位操作实现形态学腐蚀膨胀。最后利用二值图像的特性，构造出32bit整数形成的分段图，在该分段图上进行并行的位操作来实现算法的性能提升。该算法相比于传统的形态学处理操作，在性能上有了大幅提升。二值图像分辨率越大，本算法的性能提升越明显。同时，由于本算法只是对整数操作，并不关心整数的具体内容，因此，二值图像本身的纹理复杂程度并不会影响本算法的性能，这也是对一些需要首先进行边界检测的形态学处理方法的提升。

参考文献：

[1]RAFAELC. 数字图像处理[M].3版.北京：电子工业出版社，2013.

[2]杨琨，曾立波，王殿成.数学形态学腐蚀膨胀运算的快速算法[J].计算机工程与应用，2005(34)：54-56.

[3]陆宗琪，朱煜.数学形态学腐蚀膨胀运算的快速算法[C]//第十三届全国图象图形学学术会议. 北京：清华大学出版社，2006：15-20.

[4]CHENGXinyu.Fastbinarydilation/erosionalgorithmusingreferencepoints[C]//Proc.InternationalConferenceonNetworkingandDigitalSociety. [S.l.]：IEEEPress，2009：87-90.

[5]MATTHEWJ.Fastmorphologicalimageprocessingopen-sourceextensionsforGPUprocessingwithCUDA[J].IEEEjournalofselectedtopicsinsignalprocessing，2012(6)：849-855.

Fastparallelalgorithmofmorphologyoperationbasedonelementsubsection

CHENGKai1，CHENGYong2

(1. Institute of Image Communication & Network Engineering， Shanghai Jiaotong University， Shanghai 200240， China2.Institute of Communication Engineering， Nanjing Institute of Technology，Nanjing 211167， China)

Abstract:In this paper， a fast algorithm of mathematical morphology dilation and erosion operation with the structuring element of 4-connectivity and 8-connectivity is presented. Decomposing the structure element into two directions， dilation and erosion are obtained through bit manipulation. Besides， utilizing the characteristic of binary image， an integer is obtained connecting several image pixels， which helps improve the performance. The new algorithm is simpler to optimizing design， convenient to realize and has higher performance.

Key words:subsection； parallel； dilation； erosion

中图分类号:TN911.73

文献标志码:A

DOI：10.16280/j.videoe.2016.03.006

基金项目：江苏省自然科学基金项目(BK20131342)

作者简介：

程楷(1991— )，硕士生，主要研究数字图像处理、计算机视觉。

责任编辑：时雯

收稿日期：2015-11-13

文献引用格式：程楷，程勇.基于结构元素分解的二值形态学并行快速算法[J].电视技术,2016，40(3)：26-29.

CHENGK，CHENGY.Fastparallelalgorithmofmorphologyoperationbasedonelementsubsection[J].Videoengineering,2016,40(3)：26-29.