基于“六步三段两分支”教学过程模式的数学课堂教学设计

姜明

【摘 要】 介绍“六步三段两分支”教学过程模式，结合《三角形中位线》一节的教学设计，阐述“六步三段两分支”教学过程模式在初中数学课堂教学设计中的应用.

【关键词】 “六步三段两分支”；三角形中位线；变式练习

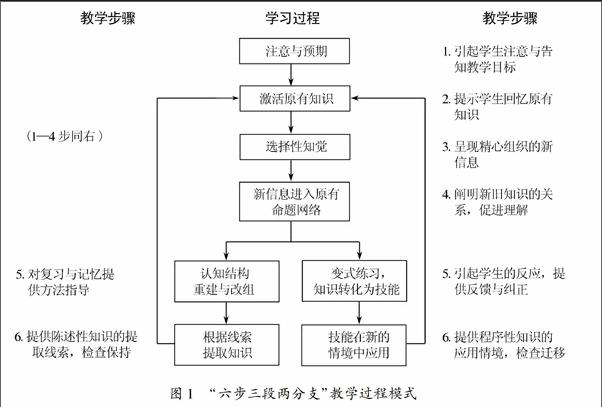
华东师范大学皮连生教授根据新型智育理论（该理论以现代认知心理学的广义知识观为核心），吸取加涅的课堂教学过程模式的优点，在《智育心理学》一书中提出了“六步三段两分支”教学过程模式[1]，如图1.

该模式示意图中间一列代表学生的学习过程，左右两侧表示针对学习过程所采取的教学步骤.其中“六步”是指：不论哪类知识，其完整的学习过程都经过图1的6个步骤，同时也就相应地有6个教学步骤.“三段”是学习和教学的6个步骤可概括为3段：1至4步为第1段，中心任务是知识的理解；第5步为第2段，中心任务是知识的巩固和转化；第6步为第3段，中心任务是知识的提取和运用.“两分支”是指：陈述性知识和程序性知识的教学过程的前4步相同，从第5步开始出现分支，右边一支表示程序性知识的变式练习和迁移，左边一支表示陈述性知识的巩固和提取.

该课堂教学模式与传统教学模式相比，最大的特点在于该模式反映了知识分类学习的思想.在数学教学中，教师可按照该模式中的各阶段和步骤进行有针对性的教学设计.对于数学中陈述性知识的教学宜采用模式中的1至4步及左侧的5、6步，而对于程序性知识应采用1至4步及右侧的5、6步.该模式能清楚地解释基本课型的结构，有利于我们依据该模式来设计课的构成、顺序和时间分配，更重要的是避免了僵硬的模式束缚，强调根据不同的知识类型设计不同的教学任务，因此，在数学课堂教学设计中具有较强的指导作用.本文以“三角形中位线”一节为例探究该模式在初中数学课堂教学设计中的应用. 1 知识的理解和掌握阶段

这一阶段主要任务是如何促进学生对新知识的理解和掌握，主要分为四个步骤，分别是引起学生注意与告知教学目标，提示学生回忆原有知识，呈现精心组织的新信息，阐明新旧知识的联系.

1.1 引起学生注意与告知教学目标

这一步对应学习过程中的注意与预期.在这一步中，教学的任务是激发学习兴趣，调动学习动机，从而引发学生的注意.注意是信息进入人脑的门户，没有注意，不可能产生有意识的学习，所以教师应根据学生的年龄特征采用各种形式吸引学生的注意.引发学生注意的方法很多，可通过设计悬念、类比联想、实验演示、使用教具等方法引发注意.教学目标可以根据需要调至合适时候再告知，不一定非要在此步中告知.

教学设计 小亮要想测量一个人工湖（见后面的图10）最宽的地方的长度，如何测量呢？

设计意图 通过这样的设计，引发学生的思考：问题应该如何解决呢？然而根据学生已有的知识是无法解决的，此时教师再告诉学生：等学完本节课的知识后就知道如何解决了.通过设置悬念的方法调动学生的学习动机，引发学生的注意.

1.2 提示学生回忆原有知识

这一步对应学习过程中的激活原有知识.在这一步中，教学的任务是帮助学生回忆与新知识有关的原有知识，否则学生只能机械的学习.认知心理学认为，决定有意义学习出现的唯一最重要条件是学生原有知识的性质，包括学生在学习新知识时，其认知结构是否具备相应的知识准备，以及原有知识是否巩固等.教师可通过复习、提问、操作或测验等方式让学生回忆起原有知识[2].

教学设计 请同学们说说平行四边形有哪些性质？判定一个四边形是平行四边形有哪些方法？

设计意图 通过回忆平行四边形的性质和判定方法，激活原有知识，同时为后续探索和证明三角形中位线的性质作铺垫，因为三角形中位线的性质主要是通过平行四边形的性质得到.

1.3 呈现精心组织的新信息

这一步对应学习过程中的选择性知觉.在这一步中，教学的任务是使学生感受新知识的信息刺激，使新知识能被学生有选择地感知.为此，教师可以根据新知识性质的不同，分别以不同的方式呈现，如教师呈现例证，教师对概念的言语界定，学生动手操作等形式.教师如能合理利用多媒体呈现教学内容，则能使学生产生良好的知觉效果[3].

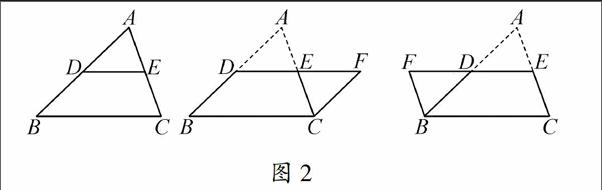
教学设计 1.同学们，请拿出一张纸画一个三角形并把它剪下来.请大家尝试：剪一刀将三角形剪成一张三角形纸片和一张梯形纸片，并将它们拼成一个平形四边形，你能做到吗？（然后请学生说说是怎么做的，教师利用多媒体演示拼接过程，如图2所示.）

图2

2.图2中线段DE是△ABC的中位线，这节课我们来学习三角形中位线.同学们能不能给三角形中位线下个定义？（学生叙述或在教师指导下叙述三角形中位线定义.）

3.三角形中位线有什么性质呢？请看图3，在△ABC中，D是AB的中点，E是AC的中点，试猜想DE和BC的关系并证明，可以小组讨论.

4.同学们能不能总结三角形中位线的性质？（学生叙述或在教师指导下叙述三角形中位线定理.）

设计意图 通过学生动手操作，感受三角形中位线与平行四边形之间的关系，为后面探索和证明三角形中位线的性质进一步作铺垫.通过学生自主探究，小组合作，既得到了三角形中位线定理，接受了新信息，又经历了数学知识的形成过程，加深了对三角形中位线定理的认识.

1.4 阐明新旧知识的联系

这一步对应学习过程中新信息进入原有命题网络.在这一步中，教学的任务是讲明新旧知识的联系，从而帮助学生理解新知识.新知识进入学习者已有知识结构的适当部位，学生认知结构中已有的图式同化新知识，使原有图式不断重新建构.例如在学习概念时，要知道新概念与其他概念间的关系，即不仅要记住新概念的定义，还要明确它的上位概念、下位概念和并列概念，明确它在概念网络中的地位.

教学设计 三角形中位线与三角形中线有何联系和区别？

设计意图 学生通过对比会很容易发现它们共同点：都与中点有关，不同点：中位线的两个端点都是中点，中线的一个端点是中点，另一个端点是三角形的顶点.通过这样的比较，使学生在原有认知结构中同化了中位线新知识，让中位线知识进入学生已有知识结构的适当部位，避免了学生以后混淆中位线和中线这两个概念，加深了对中位线概念的认识.

2 知识的巩固与转化阶段

这一阶段主要任务是如何促进知识的巩固与转化.程序性知识与陈述性知识在此阶段开始分化，掌握的新知识一部分作为陈述性知识继续贮存于原有命题网络中；另一部分通过各种变式练习转化成程序性知识.对于陈述性知识，教师要通过适当的复习，对学生的记忆进行指导，使学生掌握的知识得到巩固，常用的策略有精加工、谐音法、词头记忆法等.对于程序性知识，教师一个任务是促进学生构建知识间的联系，从而巩固新知识，另一个任务是要使学生完成由陈述性知识向学习技能的转变，常用的策略有启发式提问、变式练习等.通过启发式提问，促进学生建立新知识内部的联系；通过变式练习，促进学生在多种多样的情境中训练，加深对新知识的理解，实现对学习的控制逐渐由教师向学生转移.

3 知识的提取与应用阶段

这一阶段主要任务是如何促进知识的提取与应用，即知识的巩固与迁移.对于陈述性知识，重要任务是与遗忘作斗争，克服遗忘的常用的策略有：复习、重复、反馈.复习可以是间隔复习，可以采用游戏、竞争或应用情境等形式进行；反馈可以采用矫正性反馈，即当堂提问，若回答错误，则当堂给予矫正[2].对于程序性知识，重要任务是新知识的迁移，常用的策略是进行独立练习.在进行独立练习时教师要注意三点：一是确定何时由有指导的练习过渡到独立练习，当学生自信而又流畅地进行练习而不是犹豫不决地进行练习时，就可以过渡到独立练习了；二是安排独立练习的形式，独立练习题可以是变式练习题，防止学生将相关的技能理解成只能在特定情境中运用的倾向；三是给予反馈，如果课堂教学时间够用，可以当堂反馈，让教师及时了解学生学习的情况.

教学设计

1.同学们知道如何解决本节课开始时提出的问题吗？

2.小亮要想测量一个人工湖最宽的地方的长度，他想了这样一个办法，如图10，在湖边的岸上任意选一点C，连接AC，BC，取AC的中点E，取BC的中点F，连接EF，量得EF=20米，则湖宽AB等于多少米，为什么？

2.如图11，顺次连接四边形ABCD各边中点得到四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）.

3.如图12，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点.

4.如图13，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，连接MN，AB=5，BC=10，MN=2，求△ABC的周长.

设计意图

练习题的设计体现了由易到难、变化多样、紧扣新知识的特点.通过对这些练习题的解答，考查了学生应用新知识的能力，反馈了学生课堂学习的情况，为教师后续的教学活动的开展作准备.

参考文献

[1] 皮连生.智育心理学[M].北京：人民教育出版社，1998

[2] 皮连生.教学设计[M].北京：高等教育出版社，2000

[3] 伍慧娇.数学课程“六步三段两分支”教学过程模式探析[J].湖南工业大学学报，2007，21（3）：98-100