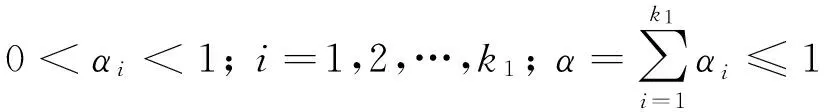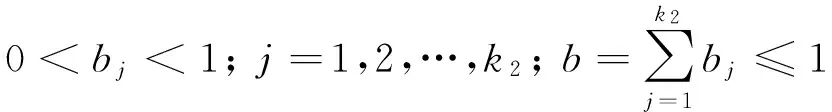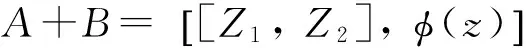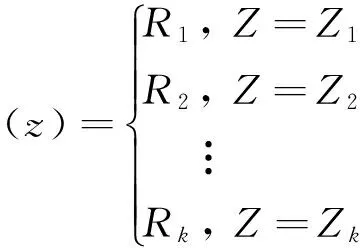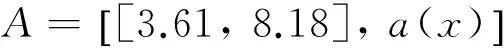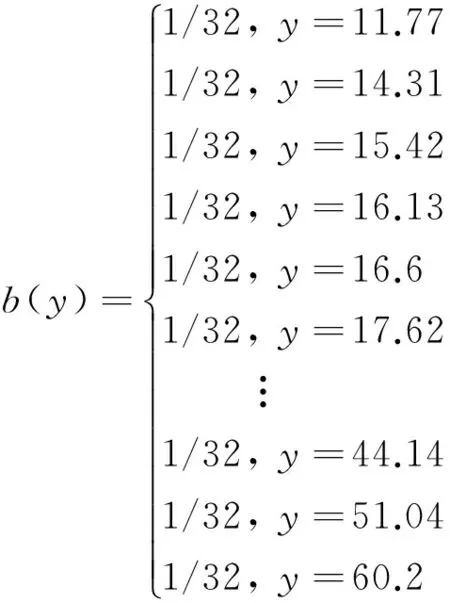未确知数学法在蚀变岩密集带综合变形模量取值中的应用

赵梓彤, 沈军辉, 徐　鹏, 祝华平, 魏　伟

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 成都 610059;2.中国电建集团 成都勘测设计研究院有限公司,成都 610072)

未确知数学法在蚀变岩密集带综合变形模量取值中的应用

赵梓彤1, 沈军辉1, 徐鹏1, 祝华平2, 魏伟1

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 成都 610059;2.中国电建集团 成都勘测设计研究院有限公司,成都 610072)

[摘要]针对雅砻江孟底沟水电站坝基中蚀变岩密集带岩体综合变形模量取值的不确定性，采用一种不确定信息的处理方法——未确知数学法来计算其综合变形模量。以典型蚀变岩密集带为例,计算结果表明其综合变形模量取值在17～18 GPa时，可信度最大，保证率为83.80%。相比非线性回归法及算术平均法等传统方法的计算值为19.40 GPa、保证率仅为61.36%而言，未确知数学法的计算结果更为合理、可靠。

[关键词]蚀变岩；变形模量；未确知性；保证率

拟建雅砻江孟底沟水电站坝基为燕山早期的花岗闪长岩，岩体中密集发育有沿一组裂隙发生热液蚀变形成的蚀变岩带，蚀变岩带与原岩花岗闪长岩呈“互层状”产出，构成蚀变岩密集带。由于蚀变岩带均具有不同程度的黏土化，使其变形模量大大低于原岩(花岗闪长岩)，从而形成了软硬相间的“互层状”组合岩体。

蚀变岩密集带的综合变形模量本身是一个确定值，但由于受蚀变岩在整个带中的所占比例、宽度及蚀变程度等不确定因素的影响，且现场只能做有限组存在一定误差的变形试验，使其综合变形模量的计算具有很多不确定性。周火明、李维树、Kayabasi、Gokceoglu等国内外学者对于这种软硬相间的“互层状”岩体综合变形模量的计算往往采用经验类比法、非线性回归法、算术平均法等[1-10]；但这些方法只能在一定程度上避免试验过程中的随机误差，不能避免由复杂地质条件(本文即蚀变岩所占比例、宽度及蚀变程度不一)引起的误差。因此，如何最大限度利用有限的实验数据来正确计算软硬相间互层状岩体的综合变形模量具有重要意义。

未确知数学法是一种不确定信息处理方法，其中未确知性是指由于条件所限，对客观存在的事物主观认识上的不确定性[11-13]，这与蚀变岩密集带的综合变形模量计算的不确定性正好吻合，故本文采用该方法对其进行求解。首先，根据未确知数学法方差、期望的性质推算出软、硬岩各自在综合变形模量中所占权重，然后运用常规的未确知数学法计算出所有的可能取值，进而对所有可能取值进行统计分析及合理分段，并计算出每段取值的置信度及保证率。成果对软硬相间“互层状”岩体的综合变形模量取值有一定理论意义，对孟底沟水电站坝基蚀变岩密集带的综合变形模量取值具有实际意义。

1未确知数学理论体系

未确知数学最早由王光远教授在1990年提出，之后经过刘开第、吴和琴教授[14]等的众多努力，建立了未确知数学的理论体系[15]。

1.1未确知有理数概念

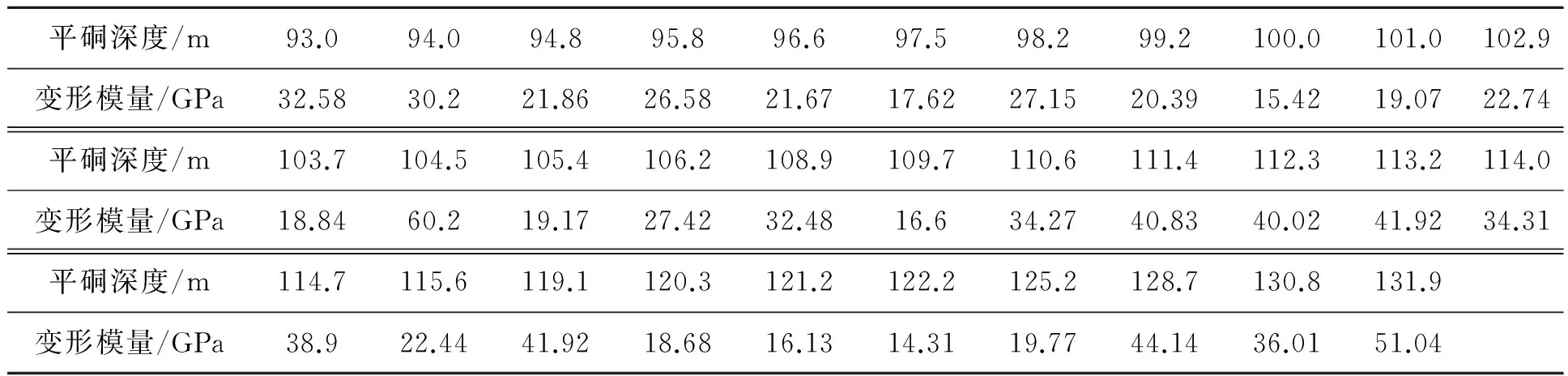
对任意闭区间[a,b],a=x1

且

则称[a,b]和φ(x)构成一个n阶未确知有理数，记作[[a,b],φ(x)]，称α、[a,b]和φ(x)分别为未确知有理数的总可信度、取值区间和可信度分布函数。

1.2未确知有理数计算

设A和B为未确知有理数，其中

A=[[a1,a2],a(x)]

则A与B的可能值带边和矩阵为

x1x1+y1x1+y2…x1+yj…x1+ymx2x2+y1x2+y2…x2+yj…x2+ym︙︙︙︙︙︙︙xixi+y1xi+y2…xi+yj…xi+ym︙︙︙︙︙︙︙xkxk+y1xk+y2…xk+yj…xk+ym+y1y2…yj…ym

1.3未确知有理数期望与方差

在前文已设未确知有理数A，其期望值公式如下

方差公式如下

2未确知有理数的工程应用

拟建雅砻江孟底沟水电站坝基局部发育有热液蚀变形成的蚀变岩密集带，本文以PD203平硐93.4～132.0 m处ACZ02蚀变岩密集带为例，对其综合变形模量进行研究。该段发育有11条蚀变程度不一的蚀变岩带，其中蚀变岩带之间未蚀变的微新花岗闪长岩占整个带宽的47%，强黏土化蚀变岩占30%，弱黏土化蚀变岩占23%。蚀变岩、围岩变形模量值分别列于表1、表2中。

运用未确知有理数来计算蚀变岩密集带的综合变形模量值。设蚀变岩为未确知有理数A，围岩为未确知有理数B，则有如下公式成立在地质工程中对未确知数学法的运用中一般取影响因素所占权重均等，但在ACZ02区内综合变形模量计算公式中，由于蚀变岩及围岩的力学性质(即变形模量)差异较大，故不能认为两者的权重均衡分布，需进一步推导求解。以下过程即是分析两者各自所占权重的方法，设蚀变岩权重为m，围岩权重为n，密集蚀变带为未确知有理数Z, 则

表1　ACZ02蚀变岩密集带内蚀变岩变形模量

平硐深度/m102.0107.2108.0116.4117.1118.0123.3124.3126.2127.5129.8变形模量/GPa8.058.184.915.504.104.573.613.885.183.615.15

表2　ACZ02蚀变岩密集带内围岩变形模量

E(Z)=mE(A)+nE(B)

(1)

由未确知期望E(A+B)=E(A)+E(B)可知

E(Z)=E(mA+nB)

(2)

式(1)及式(2)中E(Z)、E(A)、E(B)分别为密集蚀变带、蚀变岩及围岩的期望值。

为使密集蚀变带的综合变形模量接近真实值，即使D(Z)的绝对值取值最小，其计算公式为

D(Z)=D(mA+nB)

(3)

根据未确知方差的性质可知

D(Z)=m2D(A)+n2D(B)

(4)

且

(5)

(6)

将(5)和(6)两式代入(4)式可得

(7)

且m+n=1，将表1和表2中的数据代入(7)式计算可得

D(Z)=28.93m+963.90n-861.84

(8)

在式(3)～式(8)中D(Z)、D(A)、D(B)分别为密集蚀变带、蚀变岩及围岩的方差值。

当|D(Z)|的绝对值为0时，方差取最小值，此时得出m≈0.11，n≈0.89；最后将所得m和n值代入(1)式即可得出蚀变岩密集带综合变形模量可能取值共计352组。表3仅列出了其中的132组数据，其中EA、EB、E0分别表示蚀变岩、围岩及蚀变岩密集带变形模量值。将所有的可能模量取值进行分段，并将A与B的可能值带边和矩阵中的加号换成乘号，最后将可能值替换成可信度，即可得出不同分段模量对应的可信度，如表4所示。

由于大型变形试验费用高、工期长，故仅对坝址区不同蚀变程度的典型岩体做了30组刚性承压板法变形试验，并做了配套的声波测试。对实测变形资料统计得微新花岗闪长岩及蚀变岩的变形模量分别为28.90 GPa和7.02 GPa。采用传统的声波-变形模量相关性分析法与算术平均法相结合的方法，得出ACZ02蚀变岩密集带的综合变形模量值为19.40 GPa；查阅表4，得相应数据段的可信度为4.82%；计算得保证率仅为61.36%，其保证率相对较低。传统方法所采用的有限的变形试验结果仅具有测点局部的代表性，尤其是对于坝址区具有蚀变岩所占比例、宽度及蚀变程度等各不相同的蚀变岩密集带，这种根据局部的有限试验资料经相关分析得到的成果，很难代表某一特定蚀变岩密集带的变形特性，表明传统方法不能避免由复杂地质条件引起的不确定性误差。

表3　蚀变岩密集带区综合变形模量可能取值(E/GPa)

表4　变形模量不同取值可信度

根据表4可以看出，当ACZ02的综合变形模量在17～18 GPa区间时，其可信度最大，此时的保证率可达83.80%。据此，用未确知数学法得到ACZ02的综合变形模量值为17～18 GPa，相比坝址区微新花岗闪长岩的变形模量值28.90 GPa，ACZ02蚀变岩密集带由于黏土化蚀变致使岩体的变形模量值降低了37.72%～41.18%，表明岩石的蚀变对整个岩体的综合变形模量值和变形特性影响较大。

3结 论

a.根据未确知数学法的期望、方差，推算出蚀变岩、微新花岗闪长岩在典型蚀变岩密集带ACZ02综合变形模量的贡献权重分别为0.11和0.89。表明蚀变岩带的存在，对岩体变形模量的影响较大。

b.采用未确知数学法得到的典型蚀变岩密集带ACZ02的综合变形模量为17～18 GPa，其保证率为83.80%；根据传统方法得到的变形模量为19.40 GPa，其保证率仅为61.36%。表明对于这种软硬相间“互层状”岩体综合变形模量的计算取值，未确知数学法相比传统方法更加合理可靠。因黏土化蚀变致使蚀变岩密集带ACZ02岩体的变形模量值降低了37.72%～41.18%，表明蚀变对岩体的变形特性影响较大。

c.尽管未确知数学法的计算过程较复杂，但其结果稳定、精细，每一个数据段的取值都能找到对应的置信度，可以快速找出置信度最大时的取值及其相应的保证率。本项研究针对蚀变岩密集带地质条件的差异性及不确定性，采用处理各种不确定信息的未确知数学法研究其综合变形模量，是对未确知数学法在地质工程领域应用的一种探索，其在地质工程领域中的进一步应用值得期待。

[参考文献]

[1] 苗朝，沈军辉，李文纲，等.大岗山坝区辉绿岩脉蚀变泥化特征及机理研究[J].工程地质学报，2014，22(1)：130-136.

Miao Z, Shen J H, Li W G,etal. Argillization and mechanism characteristics of altered-dolerite in Dagangshan Hydropower Station [J]. Journal of Engineering Geology, 2014, 22(1): 130-136. (In Chinese)

[2] 李维树,周火明,王复兴.确定工程岩体宏观变形参数的方法探讨[J].岩石力学与工程学报，2001，20(增刊)：1758-1761.

Li W S, Zhou H M, Wang F X. Study on determination method of macroscopic deformation parameter for engineering rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(Supplement): 1758-1761. (In Chinese)

[3] 宋彦辉，巨广宏，孙苗.岩体波速与坝基岩体变形模量关系[J].岩土力学学报，2011，32(5)：1507-1512.

Song Y H, Ju G H, Sun M. Relationship between wave velocity and deformation modulus of rock masses[J]. Rock and Soil Mechanics, 2011, 32(5): 1507-1512. (In Chinese)

[4] 周火明，孔祥辉.水利水电工程岩石力学参数取值问题与对策[J].长江科学院院报，2006，23(4):37-40.

Zhou H M, Kong X H. Problem and countermeasures on parameter selection of rock mechanics in water conservancy and hydropower projects [J]. Journal of Yangtze River Scientific Research Institute, 2006, 23(4): 37-40. (In Chinese)

[5] 周火明，盛谦，陈殊伟.层状复合岩体变形试验尺寸效应的数值模拟[J].岩石力学与工程学报，2004，23(2)：289-292．

Zhou H M, Sheng Q, Chen S W. Numerical simulation of size-effect in deformation test of layer composite rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2): 289-292. (In Chinese)

[6] Gokceoglu C, Sonmez H, Kayabasi A. Predicting the deformation moduli of rock masses[J]. International Journal of Rock Mechnics and Mining Sciences, 2003, 40(5): 701-710.

[7] Zhang L Y, Einstein H H. Using RQD to estimate the deformation modulus of rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 337-341.

[8] Li C. A method for graphically presenting the deformation modulus of jointed rock masses[J]. Rock Mechanics and Rock Engineering, 2001, 34(1): 67-75.

[9] 魏玉峰，聂德新，吕生弟，等.溃曲软硬相间顺层斜坡滑移-弯曲破坏机制分析[J].成都理工大学学报(自然科学版)，2009，36(3)：287-291.

Wei Y F, Nie D X, Lyu S D,etal. The mechanism analysis of sliding-bending destruction mode of consequent bedded slop in the alternatively distributed soft and hard rock layers[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2009, 36(3): 287-291. (In Chinese)

[10] 林峰,黄润秋,严明.锦屏水电站左岸坝头边坡变形拉裂岩体稳定性评价[J].成都理工大学学报(自然科学版)，2009，36(5)：487-491.

Lin F, Huang R Q, Yan M. Stability evaluation of the deformed tension-fracture rock mass in the abutment slope on the left side bank at the Jinping hydroelectric power station in Southwest China[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2009, 36(3): 487-491. (In Chinese)

[11] 潘继斌. 未确知函数及其应用[J]. 湖北师范学院学报(自然科学版)，2002，22(3)：39-48.

Pan J B. Unascertained function and its application[J]. Journal of Hubei Normal University (Natural Science), 2002, 22(3): 39-48. (In Chinese)

[12] 岳常安，许时芬.未确知期望及其应用[J].兰州铁道学院学报，1998，17(3)：109-117.

Yue C A, Xu S F. Unascertained expectation and its applications[J]. Journal of Lanzhou Railway University, 1998, 17(3): 109-17. (In Chinese)

[13] 林建华，林泽阳.用未确知有理数确定指标主观权重方法研究[J].信息化研究学报，2014，40(3)：23-27.

Lin J H, Lin Z Y. The application of unascertained rational number to determining subjective weight of index. Electronic Engineer[J]. Journal of Information Technology Research, 2014, 40(3): 23-27. (In Chinese)

[14] 刘开第，吴和琴.不确定性信息数学处理及应用[M].北京:科学出版社，1999.

Liu K D, Wu H Q. Uncertainty Information Processing and Application of Mathematics[M]. Beijing: Science Press, 1999. (In Chinese)

[15] 宋彦辉，聂德新.用未确知数学法确定某坝址岩体变形参数[J].地质与勘探，2004，40(3)：97-100.

Song Y H, Nie D X. The determination of the rock-mass deformation parameter of a certain hydrostation by using the method of the unascertained information[J]. Geology and Prospecting, 2004, 40(3): 97-100. (In Chinese)

The application of unascertained mathematics method to the extraction of integrated deformation modulus value in intensive altered rock zone

ZHAO Zi-tong1, SHEN Jun-hui1, XU Peng1, ZHU Hua-ping2, WEI Wei1

1.StateLaboratoryofGeohazardsPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,China;2.ChinaElectricPowerConstructionSurveyandDesignInstituteGroupLtd.,Chengdu610072,China

Abstract:The extraction of integrated deformation modulus value from intensive altered rock zone in Mengdigou hydropower station of Yalong River, Southwest China has a great deal of uncertainty. Therefore, a new method of unascertained mathematics is used to deal with this kind of uncertain information process and to calculate the integrated deformation modulus value in typical intensive altered rock zone ACZ02. It shows that the maximum credibility is reached when deformation modulus in intensive altered rock zone is at a value of 17～18 GPa, with assurance rate of 83.80%. Compared with traditional methods, such as nonlinear regression method and arithmetic average method, which has a calculating value of 19.40 GPa and an assurance rate of 61.36%, the use of unascertained mathematical calculation method is more reasonable and reliable. It is enables the project to have high stability guaranteed rate.

Key words:altered rock; deformation modulus; unascertained; assurance rate

DOI:10.3969/j.issn.1671-9727.2016.03.14

[文章编号]1671-9727(2016)03-0372-06

[收稿日期]2015-09-14。

[基金项目]国家自然科学基金资助项目(41572308);高等学校博士学科点专项科研联合资助项目(20125122110005)。

[通信作者]沈军辉(1964-)，男，博士，教授，博士生导师，研究方向：工程地质、环境地质, E-mail:820747923@qq.com。

[分类号]TU452

[文献标志码]A

[第一作者] 赵梓彤(1990-)，女，硕士研究生，研究方向：岩体稳定地质工程, E-mail:546363947@qq.com。