笼型三相异步电动机振动识别与分析

庄火庚

[上海电器科学研究所(集团)有限公司，上海　200063]

笼型三相异步电动机振动识别与分析

庄火庚

[上海电器科学研究所(集团)有限公司，上海200063]

摘要：为了准确识别分析三相异步电动机振动的主要影响因素，采用降电压法测量并识别了电磁振动、轴承振动以及转子动不平衡引起的振动等主要成分。结合理论分析方法，对电磁力波引起的振动进行详细的分析，较好的识别了齿谐波电磁力、偏心以及饱和等多种因素引起的振动，为电动机振动噪声的针对性改进优化提供了具有参考意义的结论。

关键词：笼型异步电动机； 振动识别； 电磁振动

0引言

异步电机的振动特性组成部分较复杂，其振动主要由气隙磁场产生的电磁振动、轴承产生的振动、转子动不平衡引起的振动等。其中，气隙磁场产生的振动主要由齿谐波磁场相互引起的谐波电磁力产生的振动，静偏心、动偏心时产生的单边磁拉力引起的振动等。因此对其振动产生的原因的准确定位和抑制较为困难。为了较好的分析识别三相异步电动机的振动特性，并采取针对性的振动抑制措施，需要对三相异步电动机的振动加速度进行频率解耦，并对各个频率下的主要振源进行识别分析，从而达到对特定频率振动针对性的抑制目的[1-2]。

本文采用降电压法分离识别一台三相异步电动机电磁力引起的振动、轴承振动及转子动不平衡引起的振动，在此基础上，结合电磁力理论分析方法，对引起电磁振动的主要电磁力的成分及产生原因进行了识别分析。

1电磁振动的分离与识别分析

1.1电磁振动的产生原因及特点

三相异步电动机电磁振动除基波磁场外主要由气隙谐波磁场相互作用产生的电磁激振力引起的。谐波电磁激振力包括齿谐波磁场相互作用产生的谐波电磁力、饱和引起的谐波磁场与基波及齿谐波磁场相互作用产生的电磁激振力、静偏心、动偏心时隙磁导发生变化引起的电磁激振力等。产生电磁力的气隙磁密的表达式为[3]

b(θ,t)=f(θ,t)λ(θ,t)

(1)

式中：f(θ,t)——气隙磁动势；

λ(θ,t)——气隙磁导。

定子绕组三相对称分布的异步电机运行时，定、转子绕组的合成磁势为

f(θ,t)=fp(θ,t)+∑fv(θ,t)+∑fμ(θ,t)

(2)

式中：fp——基波磁势；

fv——定子谐波磁势；

v——定子谐波次数；

fμ——转子谐波磁势；

μ——转子谐波次数。

各磁势均为时间和空间的变量，具体表示为

fp(θ,t)=Fpcos(pθ-ω1t-φm)

(3)

∑fv(θ,t)=∑Fvcos(νθ-ω1t-φv)

(4)

∑fμ(θ,t)=∑Fμcos(μθ-ωμt-φμ)

(5)

式中：p——电机极对数；

θ——空间机械角度；

ω1——电源角频率，相对于定子的基波旋转角频率，ω1=2πf1；

φm、φv、φμ——相应于各磁场的初相角；

当电机结构理想情况下运行时，考虑饱和及定、转子开槽带来的齿槽效应，气隙磁导可近似表示为

(6)

式中：Λ0——气隙磁导的不变部分；

λk1——转子光滑而定子开槽引起的气隙谐波磁导；

λk2——定子光滑而转子开槽引起的气隙谐波磁导；

λk1k2——定子和转子均开槽相互作用引起的气隙谐波磁导；

λksa——饱和气隙磁导。

偏心情况下气隙磁导的近似表达式为

λε(θ,t)=λ0(θ,t)[1+εecos(θ-ωet)]

(7)

式中：εe——相对偏心率；

ωe——等于转子旋转的角频率。

根据麦克斯韦张量法，电机气隙中单位面积受到的径向电磁力的瞬时值可以表示为

(8)

式中：b(θ,t)——气隙磁密；

μ0——空气磁导率。

将式(2)和式(7)带入式(1)得到气隙磁密，再将气隙磁密带入式(8)可得到径向电磁力。

忽略阶次高、幅值小的力波分量后，电动机主要径向电磁力波如表1所示。表1中，序号1为基波电磁力波；序号2、3、4为定转子齿谐波相互作用产生的力波；序号5、6为一阶定转子齿谐波与饱和谐波相互作用产生的谐波电磁力；序号7为饱磁场与基波相互作用产生的电磁力。

表1　正常运行时主要径向电磁力波

静偏心时主要径向电磁力波如表2所示。从表2中可以发现在静偏心情况下，主要径向力波的阶数每一项都±1。

表2　静偏心主要径向电磁力波

表3为动偏心情况下主要径向电磁力波的分布，其中径向力波的阶数与静偏心情况下的阶数一致，但频率在原有力波频率基础上变化±fr。

表3　动偏心主要径向电磁力波

1.2电动机电磁振动的识别与分析

本文为了分析一台Y-200L-6/4型电动机底脚4个安装螺栓附近的振动加速度，在4极空载运行状态下测量分析了该台电动机的振动加速度。该电动机基本参数如表4所示。振动加速度级测量结果频谱分析如图2所示。该电机4极空载运行时的底脚振动加速度总振级为129.19dB(10～10kHz)。

图1　空载振动加速度测试现场

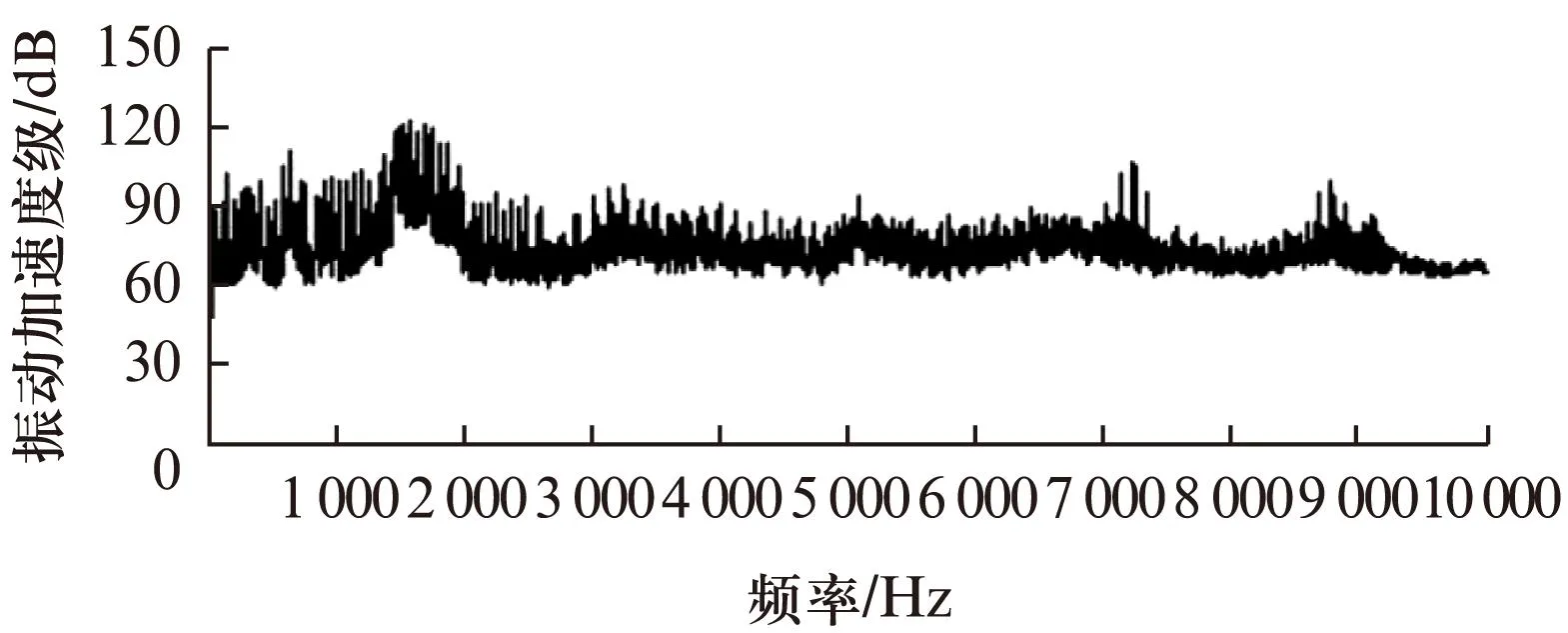
图2　空载振动加速度级测量结果

参数名称参数值额定功率/kW22额定电压/V380定子外径/mm327定子内径/mm230气隙长度/mm0.5铁心长度/mm230定/转子槽数72/58绕组联结方式Y相带60°节距15

幅值较大的主要频率点的加速度级如图3所示。

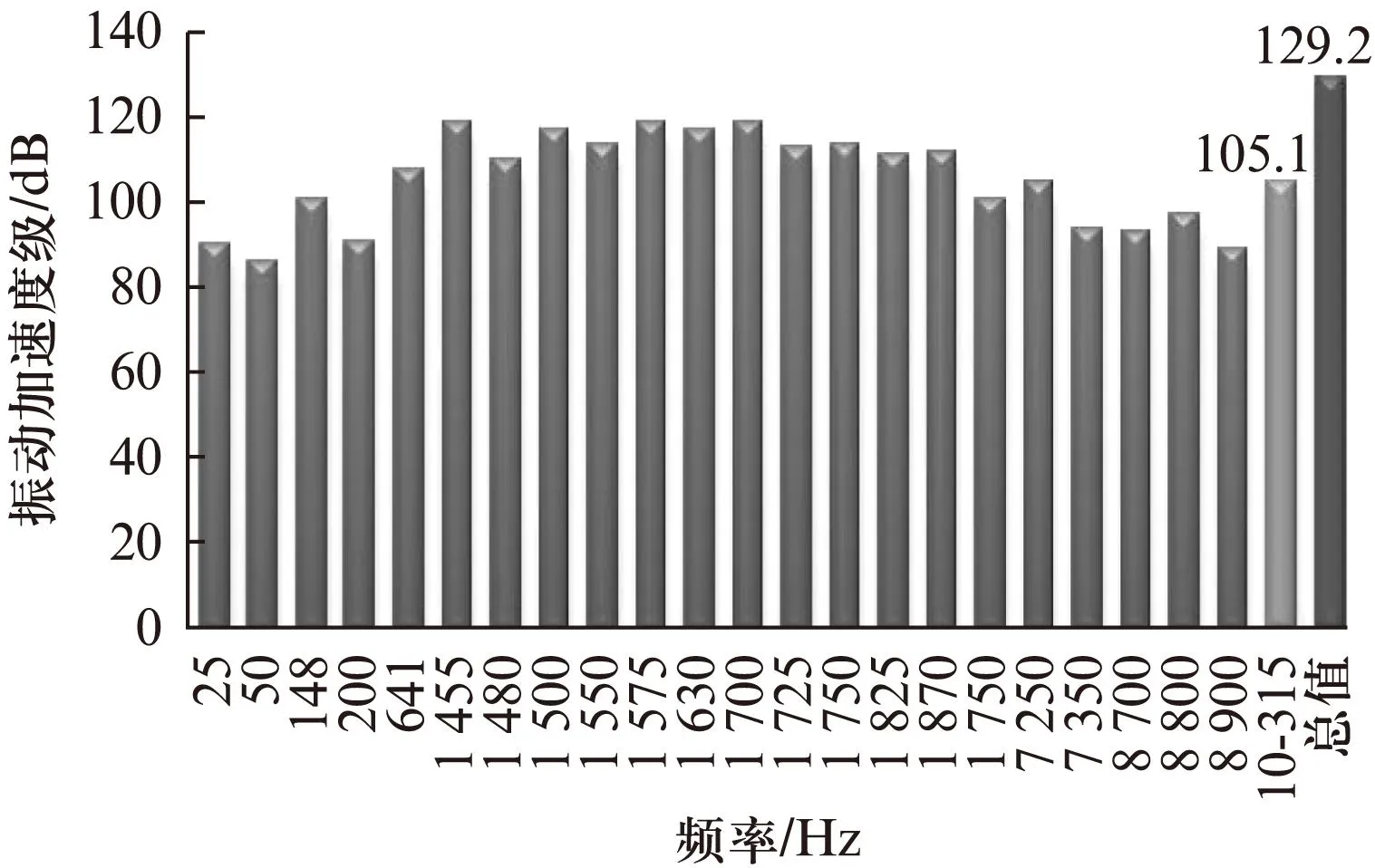
图3　底脚主要频率点的振动加速度级

为了分析造成这些频率点振动较大的原因，使用降电压法对该电机的主要振源进行了识别。

首先测量电机额定电压下稳定运行状态下的振动，然后依次测量电压降至80%和60%额定电压后稳定运行状态下的振动，最后将三者的振动频谱数据进行比较并分析振动变化规律。

将不同电压下测得的振动加速度频谱进行对比分析后可知，不同频谱曲线的峰值分布基本是一致的，只是幅值的大小会随着电压的变化而变化。

把主要频率点的振动幅值数据提取出来进行对比，如图4所示可知：50、200、1550、1725、1750、7150、7250、7350、8700、8800和8900Hz等频率处的振动值随着电压的降低而显著降低。这跟电磁力与电压之间的理论关系是相符的，故可以推断，这些频率点处的振动极有可能是由电磁力的激励而引起的。

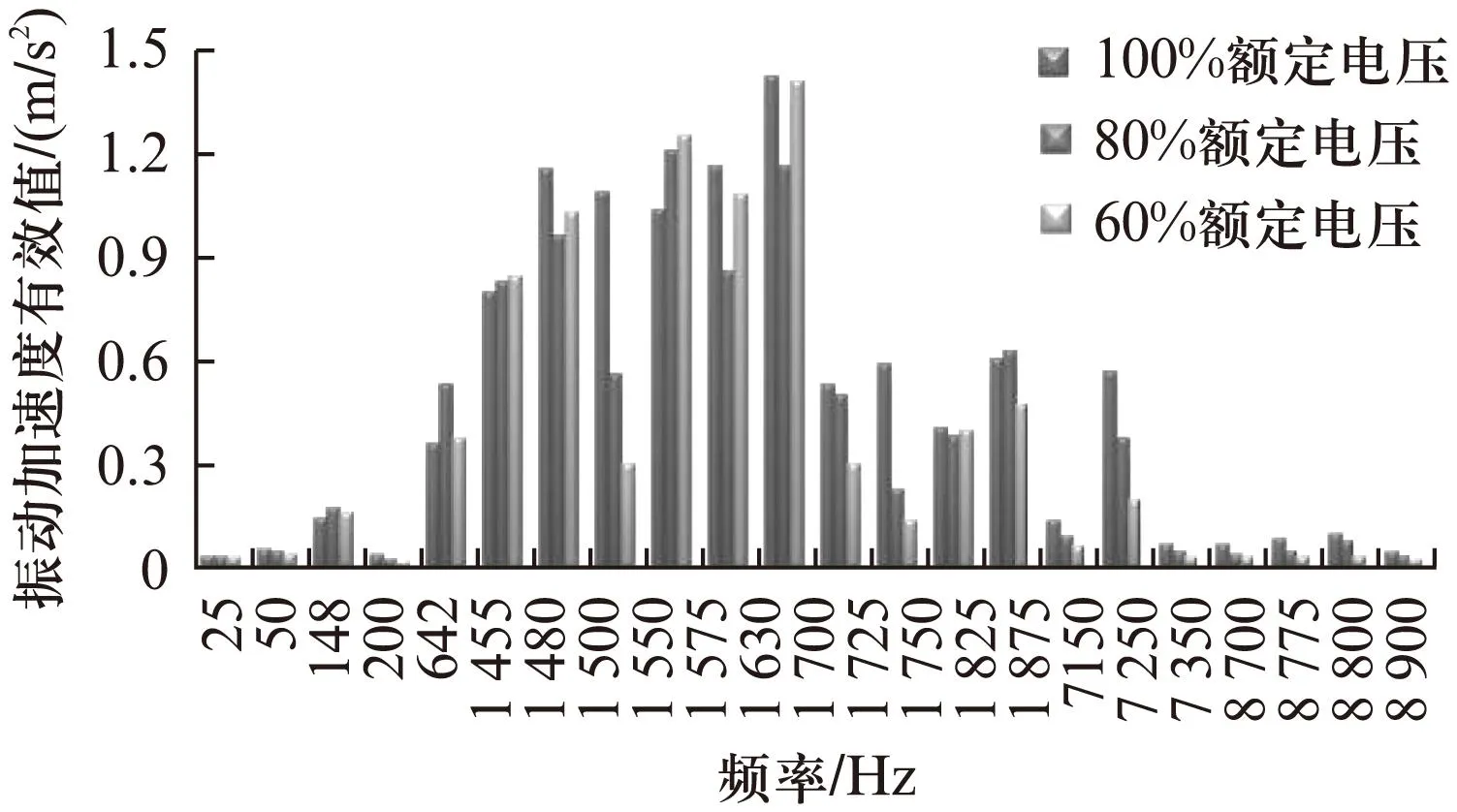
图4　主要频率点的振动加速度有效值比较

本文为了进一步分析电磁激振力引起的振动，对本台电动机进行二维场路耦合瞬态场计算后，对定子齿表面附近，在气隙处某一点的径向力进行傅里叶分析，分析结果如图5所示[4]。将图4中的主要频率振动加速度与图5中的主要力波频率对比分析后可知，1550Hz、7150Hz、7250Hz、7350Hz、8700Hz、8800Hz处的振动主要原因为齿谐波电磁力引起的。

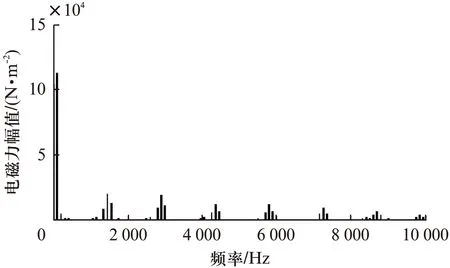
图5　气隙谐波电磁力频谱分析结果

由动偏心时的力波分析表可知，动偏心时，会在原有力波频率的基础上，增加±fr=±25Hz的力波。因此图4中的1725Hz、8775Hz的振动主要由转子动偏心引起。

由饱和引起的电磁激振力的频率特征理论分析结果可知，电机铁心饱和时会产生频率为200Hz的电磁力波。图4中的200Hz处的振动可能为饱和磁场与基波相互作用产生电磁激振力引起的振动。为了进一步明确该频率振动为饱和引起电磁激振力产生的振动，本文采用有限元分析方法，分别为铁心考虑饱和及不考虑饱和时的电动机电磁振动的计算分析。主要频率电磁力的计算结果如图6所示。从图6可看出：轭高增加或不考虑铁心饱和的情况下，气隙电磁力波中的200Hz，300Hz等谐波分量明显降低。证明该频率处的主要力波由铁心饱引起的。铁心饱和时会产生低频段的电磁激振力，从而影响低频的振动。

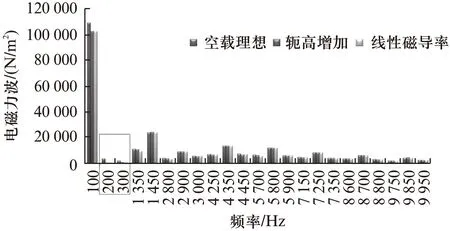
图6　气隙谐波电磁力频谱分析结果

图4中的25、1455、1500、1575、1630、1700、1875Hz等频率处的振动值不随电磁力的降低而减小，与电磁力的变化规律不相符，则极有可能与轴承等机械因素引起的振动有关。

2轴承振动的识别与分析

为了进一步判断这些频率振动是否与轴承有关，我们对电机更换新的轴承后重新做了振动加速度测量试验。更换轴承后，机脚振动加速度总振级由129.19dB降至121.1dB，降低了约8dB。

把更换新轴承前后主要频率点处的振动值进行对比，如图7所示。可以发现：1700、1455、1575、1630、1500、1870Hz等频率点处的振动都显著的得到了改善，说明更换新轴承后，轴承噪声得到了有效的抑制。

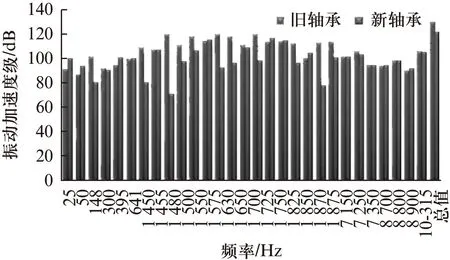
图7　换轴承前后主要频率点的结构噪声

更换轴承后的电磁振动与轴承振动的变化如图8所示。左侧为认为电磁振动的频率点，右侧为认为轴承振动的频率点。可以看到，凡是识别为轴承振动的频率点都有较为显著的改善，而识别为电磁振动的频率点则无明显变化。进一步说明了振动识别的准确性。

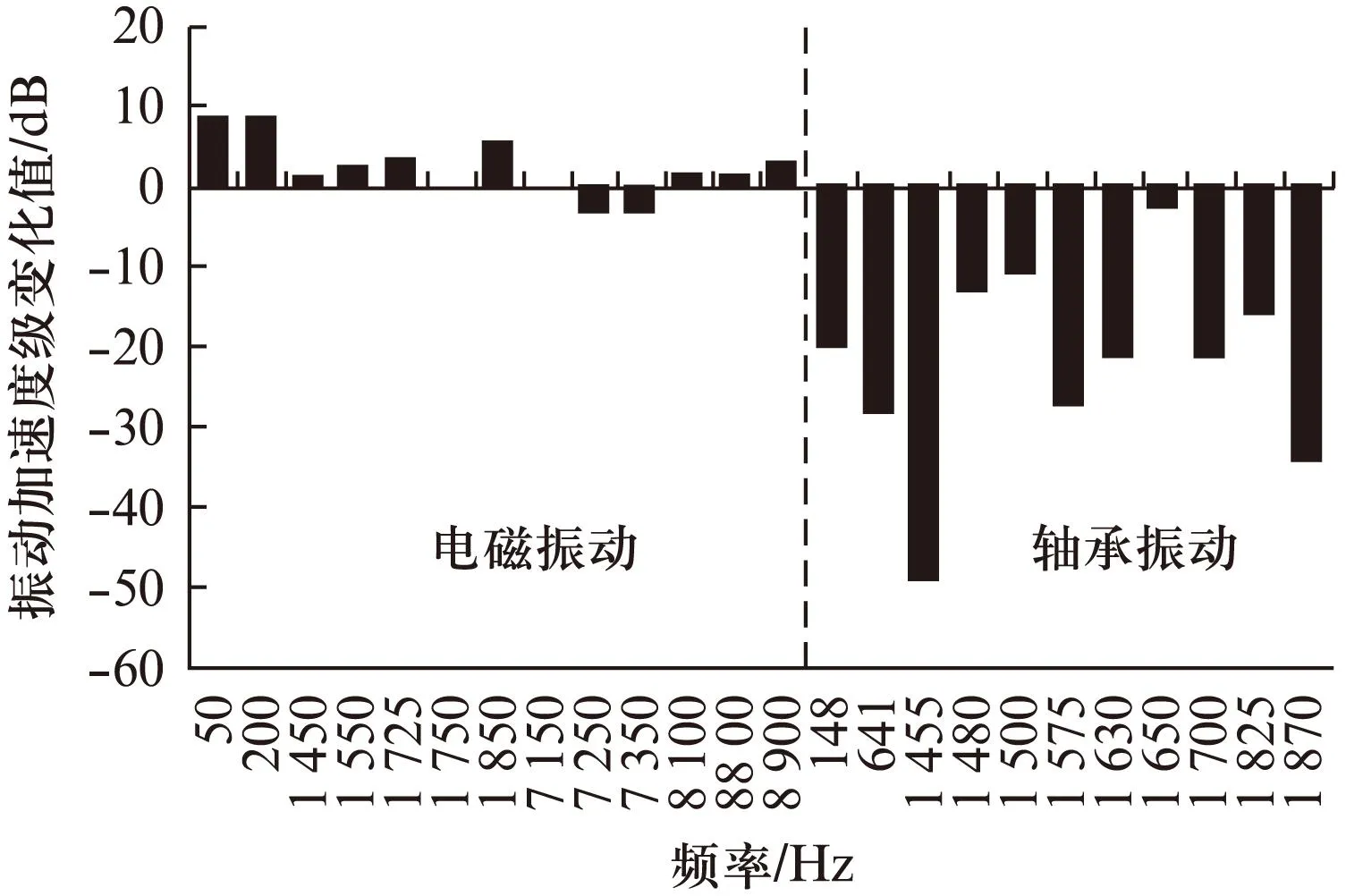
图8　换轴承前后主要频率点的振动加速度级变化量

3动平衡引起的振动的识别与分析

经过更换轴承后虽然较多频率处的振动有明显的变化，但25Hz的振动未因更换新轴承而降低，也未电磁力的变化而变化。该频率处的振动主要为动不平衡引起的振动。为了明确动平衡对电机振动的影响规律，分别对电动机转子动平衡校准和未校准动平衡情况下测量分析了一台电动机底脚振动加速度级。对比分析结果如图9所示。经过分析可知，动平衡度较差时，在转频附近(25Hz)会产生较大的振动，而在其他频率处无明显变化。通过试验验证进一步确认了25Hz处的振动为主要有转子动不平衡引起的振动。

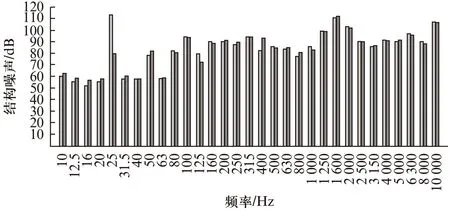
图9　动平衡对电动机底脚振动加速度的影响

4结语

降电压法对电机振动的识别起到很好的作用，可以有效的分离识别出电磁激振力引起的振动和其他机械原因的引起的振动。

在此基础上结合三相异步电动机电磁激振力产的机理分析及电磁激振力有限元分析结果可以逐一分离识别出齿谐波、偏心以及饱和等多种因素引起的电磁振动。能够为不同原因引起的振动进行针对性的改进提供明确方向。

经过更换轴承、校转子动平衡等方式可以有效的识别出了轴承或转子动不平衡引起的振动。轴承振动分布在较宽的频率范围内，而转子动不平衡量主要对其转频对应的频率的振动有显著影响。除此之外试验表明了可以经过以上方式可以达到抑制轴承引起的振动及转子动不平衡引起的振动的目的。

【参 考 文 献】

[1]陈永校，诸自强，应善成.电机噪声的分析和控制[M].杭州：浙江大学出版社，1987.

[2]朱海峰.异步电动机电磁激振力分析[D].杭州：浙江大学，2013.

[3]狄冲，鲍晓华，王汉丰，等.感应电动机混合偏心情况下径向电磁激振力的研究[J].电工技术学报，2014.29(1).138-144.

[4]王荀，邱阿瑞.笼型异步电动机径向电磁力波的有限元计算[J].电工技术学报，2012，27(7)：109-116.

Vibration Identification and Analysis of Three Phase Squirrel Cage Induction Motor

ZHUANGHuogeng

[Shanghai Electrical Apparatus Research Institute(Group)Co.， Ltd.， Shanghai 200063, China]

Abstract：In order to accurately identify the main influence factors of three-phase induction motor vibration, the electromagnetic vibration, bearing vibration and the vibration caused by rotor dynamic unbalance and other major components were analyzed by using the method of reducing the voltage. Based on the theoretical analysis method, the vibration caused by of electromagnetic force was identified and analyzed in detail, and the vibration caused by many factors, such as the electric magnetic force, the eccentricity and the saturation factor, was well recognized. It provided a reference for the further improvement and optimization of the vibration of the motor.

Key words：squirrel cage induction motor; vibration identification; electromagnetic vibration

作者简介：庄火庚(1962—)，男，高级工程师，研究方向为船用电机与电器技术。

中图分类号：TM 302

文献标志码：A

文章编号：1673-6540(2016)05- 0047- 05

收稿日期：2016-04-16