基于Laguerre模型的永磁同步电机电流预测控制*

高旭东，　许鸣珠，　栾东雪

(石家庄铁道大学 机械工程学院，河北 石家庄　050043)

基于Laguerre模型的永磁同步电机电流预测控制*

高旭东，许鸣珠，栾东雪

(石家庄铁道大学 机械工程学院，河北 石家庄050043)

摘要：提出了一种基于Laguerre模型的自适应预测控制方法。对控制算法的数学模型进行分析与优化，将该控制算法量化后，成功地应用于以DSP TMS280F2812为核心的永磁同步电机的控制平台上，并将预测控制与传统PI控制的结果进行了对比。试验结果表明，所提出的预测控制算法使永磁同步电机具有更好的动态响应特性和稳态特性。

关键词：Laguerre模型； 模型预测控制； 电流控制； 滚动优化

0引言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)相对其他类型电机来说体积小、效率高、具备高功率密度等特点，在伺服电机领域中，以其优越的控制性能在数控加工中心、机器人、航空航天、电动汽车等领域得到了广泛的应用[1]。为了提高PMSM驱动系统的性能，保证整个系统具有良好的动态响应，本文主要尝试改善交流伺服系统的内环即电流环的控制响应[2]。

PMSM电流控制的目标是使电机的电流可以快速稳定地跟踪设定值变化[3]。传统的PMSM控制采用控制器对电机的交、直轴电流分别进行控制，这样简化了控制过程，提高了控制精度。常用控制器的控制方法主要有滞环控制、滑模变结构控制、PI调节器、预测控制等[4]。其中PI控制器原理上是一种线性调节器，靠目标与实际行为之间的误差来决定控制策略，具备控制原理简单、实现方便、应用范围广、控制参数彼此独立、参数整定比较简单等优点[5]。但在应用中普遍存在超调，很难同时保证响应的稳定性和快速性，因此 PI控制器在高性能控制场合存在一定的局限性。

预测控制具有较好的鲁棒性，能够根据预测值和设定值来判断当前系统状态，做到最优控制[6]。这种控制算法与现代控制理论设计方法有明显的不同，无须知道被控对象的自身属性参数，利用在线滚动优化计算，实时地更新控制参数[7]。本文提出了一种基于Laguerre函数模型的预测控制方法，具备非参数化和参数化模型各自的优点，所需表征系统特性的参数少，在线计算量小；并且模型包含了系统的时滞和阶次信息，不需要知道系统的确定模型，能有效避免模型结构失配问题[8-10]。通过试验验证，基于Laguerre模型的预测控制器能够为交流永磁同步电机的电流环提供高性能的控制效果，并且具有很好参数鲁棒性。

1基于Laguerre模型的预测控制

Laguerre函数对模型具有较高的逼近程度，鲁棒性很强[11]。Laguerre模型离散化后可以表示为状态方程形式[8]

(1)

式中：L(k)——状态向量；

u(k)、ym(k)——模型在k时刻的输入和输出；

A、B——Laguerre 模型有关的系数矩阵，其表示意义可见文献[9]。

与所表征对象的直接联系只有系数向量C，可以通过最小二乘法在线辨识获得[8]。

考虑到目前工业控制中常用的控制器处理数据的速度和能力，以及式(1)所述的状态空间方程在控制过程中存在稳态误差的原因，本设计将控制增量加入到预测模型中[7]。基于Laguerre模型的增量型模型预测控制算法模型为

(2)

其中：

ΔL(k)=L(k)-L(k-1)

Δu(k)=u(k)-u(k-1)

由此可得

ym(k)=Δym(k)+ym(k-1)

(3)

假设预测i个周期，由式(2)可得出在未来k+i时刻模型的输出预测值ym(k+i)如下：

(4)

为了消除模型误差以及实际过程中存在的干扰导致的输出预测误差，提高预测精度，本文采用反馈矫正来修正系统未来i时刻的预估值[12]，即有

yp(k)=ym(k)+h[y(k)-ym(k)]

(5)

式中：y(k)——k时刻系统的输出；

ym(k)——k时刻模型输出；

h——反馈增益值。

设闭环优化性能准则为

(6)

来确定{Δu(k),…,Δu(k+i-1)}使系统在未来m步的输出值尽可能地接近期望值yr(k+i),i=1,2,…,p。系统的参考轨迹由式(7)确定：

yr(k+i)=αiω(k)+(1-αi)yp

(7)

式中：qi、rj——加权系数和误差权系数；

p、m——优化时域和控制时域的周期个数，一般来说有m≤p；

ω(k)——系统设定值；

α——柔化因子。

在控制过程中，并不希望施加于系统的控制增量的变化过于剧烈，所以Δu(k)的变化也作为系统函数的评价指标[6]。通过求解最优化问题，可得最优控制增量为

Δu(k)=(GTQG+R)-1GTQ[yr(k)-yp(k)]

(8)

式中：Q、R——加权矩阵。

Q=diag(q1,…,qp),R=diag(r1,…,rm)

式(8)中(GTQG+R)-1为i×i维矩阵，可以一次计算出从k到k+i-1时刻的i个控制量。但在实际执行时，由于模型误差、系统的非线性特性和干扰等因素的影响，若按式(8)计算，经过i步控制后可能会偏离参考轨迹较多。同时最优控制量在工业控制器中求解较为复杂，在具体应用中需对预测控制算法进行简化，避免多维向量的各分量同时控制，尽量使用单输入单输出系统[6]。取式(8)中第一个元素作为系统的当前控制量，从而得到k时刻系统实际控制量

u(k)=u(k-1)+Δu(k)

(9)

因此该方法被称为“滚动优化”[13]。

在模型参数确定后，状态向量L(k)可以通过模型和系统控制量输入u(k)计算得到，因而模型输出ym(k)与Laguerre系数向量C有如下线性关系：

ym(k)=CL(k)

(10)

C可以通过带遗忘因子的最小二乘法在线辨识获得

(11)

式中：0<λ<1为遗忘因子[10]。

基于Laguerre函数逼近模型的预测控制算法主要分为预测模型、反馈矫正、滚动优化及参数辨识三部分，其控制结构如图1所示。预测模型根据控制量状态对系统输出进行预测，并根据系统的反馈值和设定值进行滚动优化和参数辨识，实现了受控对象的最优控制。

2试验平台描述

为了验证本文所提预测控制算法是否可以有效地对电流环进行控制，作者将上述数学模型在PMSM控制系统上编写相应程序进行试验。建立了以TI公司研发的DSP TMS320F2812运动控制芯片为核心的PMSM伺服系统[14]，时钟频率为150MHz，系统的控制周期为50μs。驱动系统是由IGBT搭建的桥型电路，控制系统产生的SVPWM信号经过线性驱动后输出给驱动系统，再由驱动系统将信号输送给永磁同步电机。采用的PMSM参数如下：200W，36V输入，额定电流7.5A，输出转矩0.637N·m，磁极对数4，转子转动惯量J=0.189104kg·m2，线电感0.9mH，线电阻0.33Ω。控制试验平台如图2所示。采用矢量控制的控制方式对永磁同步电机进行驱动，其程序结构控制方式如图3所示。控制器软件设计选用C语言，所用的开发环境为CCS5.5，同时该开发环境可实时监测当前系统内各个变量的变化情况。

图2　PMSM控制试验平台

图3　PMSM程序结构控制方式

3控制算法优化

从控制意义上说，预测控制是一种实时的优化算法，可以做到减小开关损耗、降低开关频率、减小谐波损耗等优化目标[15]。但对于目前的工业控制器来说，由于每个采样周期内都需要对电机的电流轨迹进行预测，所需计算速度和计算精度很难达到要求，因此，对该算法在DSP上的实现做了相应优化。由式(1)、(2)可知，预测模型的参数A和B为三阶矩阵并且可以离线计算得到。为节省DSP资源，提前将A和B内的数值计算好，在程序初始化时将数值直接写入到所设定的变量中。同理，在优化算法式(8)中Q、R设置与A、B类似。

预测控制在线计算中，考虑到预测精度和计算的复杂程度，在保证预测控制品质的前提下应尽量减小预测的步长以及运算量，经过大量的实验，选择了3步优化预测，其中滚动优化的加权矩阵取值为：

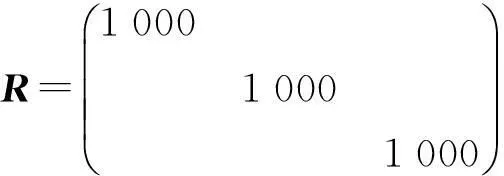
图4　d轴反馈信号动态范围

考虑到d轴的反馈信号数量级较小，DSP运算精度有限，在线辨识计算较为困难，且辨识运算后输出控制量误差大，也会影响到控制量的在线优化。遂将对d轴的参数辨识计算去除，改为定值线性计算。这样滚动优化参量也会变为定值，对d轴的控制也就变成了一阶比例滚动优化控制，既减轻了DSP的运算负担，提高了整套系统的运算速度，同时也有助于提高d轴电流的控制精度。

4试验对比

为了验证本文所提基于Laguerre模型的预测控制对电机电流的控制效果，将其与传统的常规PI控制系统在同一试验平台上进行试验比较。设定试验条件为空载1500r/min阶跃启动。通过PI参数整定的方法，以及试验调试确定q轴和轴电流环PI控制系数相同，确定PI系数为Kp=0.72，Ki=T/0.0004，其中T为DSP系统的采样周期，试验结果转速响应曲线如图5所示。采用预测控制时，通过对控制算法的优化，设定q轴预测控制参数反馈增益h=0.9，柔化因子α=0.8，遗忘因子λ=0.99；d轴预测控制参数反馈增益h=0.9，柔化因子α=0.95。经过试验，其转速响应曲线如图6所示。

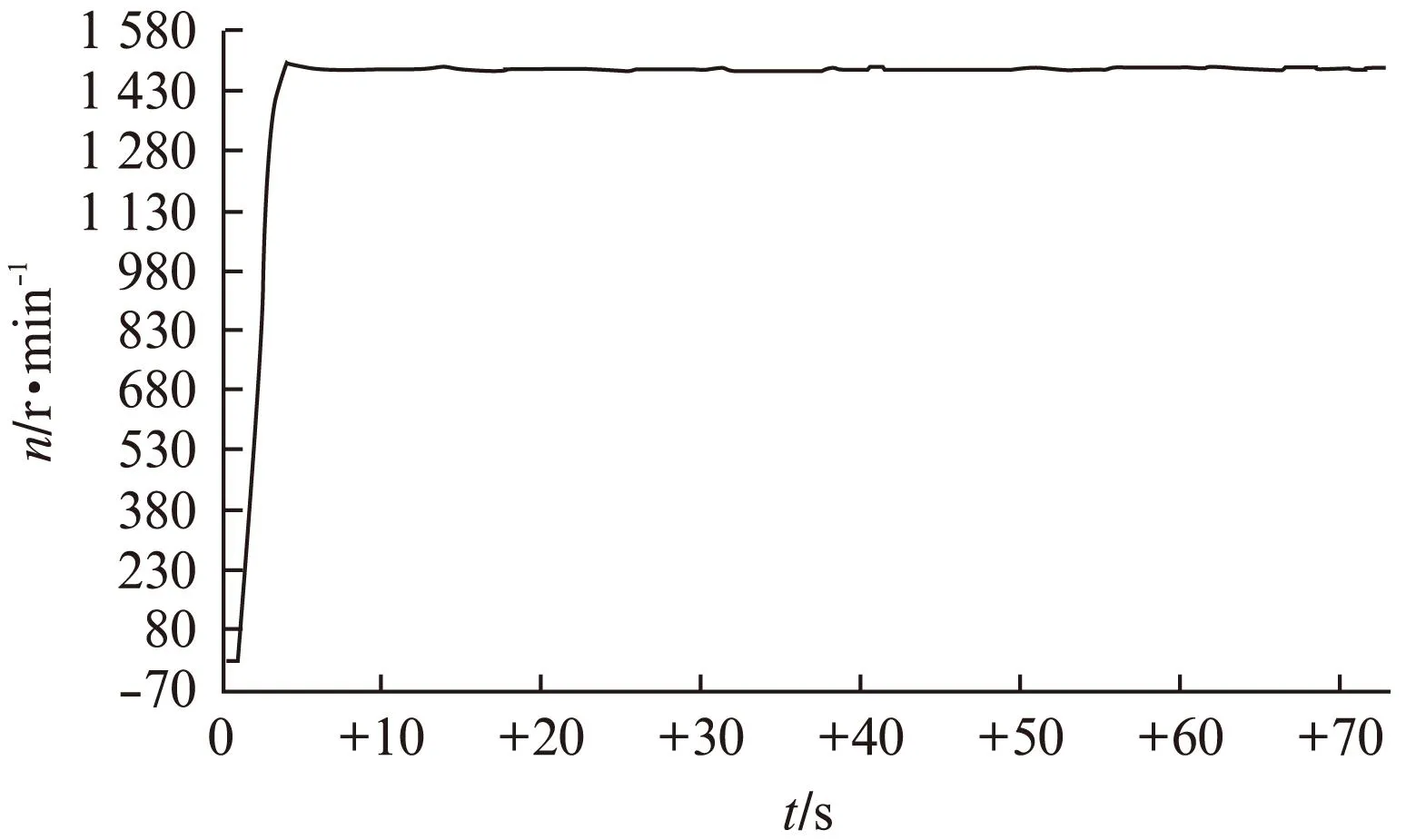
图5　基于PI控制器速度阶跃响应图

图6　基于Laguerre模型预测控制速度阶跃响应图

从图5、图6中可以看出，预测控制的速度响应时间相比于PI控制器的响应时间要长，主要原因是预测模型要比PI控制模型要大，运算量相应地也会变大，导致运算周期变大。但预测模型的控制量输出更加精确，使电机速度响应更加柔和、稳定、无超调量，并且响应时间也在系统响应允许的范围内。在稳态时，预测控制系统速度稳定，几乎无抖动，而PI控制系统中电机转速在误差范围内有波动且有明显的振荡，预测控制的控制效果要明显好于传统PI控制。

上述试验是在没有精确整定Q、R矩阵以及反馈增益值h的情况下得到的，在实际应用中还可以进一步调整，提高精度。图7是把Q、R矩阵的值设定为原值的一半时的速度响应曲线。从曲线的响应速度和正常运行时曲线的波动情况来看，其效果也明显优于传统的PI控制。可以看出预测控制对滚动优化的参数也具有较强的鲁棒性，系数矩阵的变化，对控制效果影响较小。

图7　PMSM速度响应曲线(Q和R矩阵参数值为原来的一半)

5结语

本文基于Laguerre函数模型提出针对永磁同步电机电流环的预测控制方法，在方案实现时，可以不需要知道具体的系统模型的参数和结构，通过在线辨识计算，便可以实现自适应控制，具有很强的鲁棒性。通过对模型算法的优化，DSP系统完全可以在规定时间内将控制量计算输出，实现期望的控制效果。通过与PI控制响应结果对比，可以发现其控制性能完全优于传统PI控制，运算量也在可以接受的范围内。因此本文提出的预测控制方法可以更精确地控制电机的电流，使系统具有良好的动态特性和稳态特性，具有较强的实用价值。

【参 考 文 献】

[1]李永东,张猛.高性能交流永磁同步电机伺服系统现状[J].伺服控制,2008(1)：34-37.

[2]HASSAN A A, KASSEM A M. Modeling, Simulation and performance improvements of a PMSM based on unctional model predictive control[J]. Arab J Sci Eng，2013,38(11)：3071-3079.

[3]牛里,杨明,刘可述,等.永磁同步电机电流预测控制算法[J].中国电机工程学报,2012,32(6)：131-137.

[4]王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3)：50-55.

[5]赵景波.MATLAB控制系统仿真与设计[M].北京：机械工业出版社，2010.

[6]郑泽东,王奎,李永东,等.采用模型预测控制的交流电机电流控制器[J].电工技术学报,2013,28(11)：118-123.

[7]姚伟,孙海顺,文劲宇,等.基于Laguerre模型的过热汽温自适应预测PI控制系统[J].中国电机工程学报,2012,32(5)：119-125.

[8]许鸣珠，刘贺平，李晓理，等.过热汽温的稳定自适应预函数控制[J].中国电机工程学报，2007，27(11)：88-92.

[9]许鸣珠,刘贺平,王允建.基于Laguerre模型的预测函数控制及其稳定性分析[J].控制与决策,2008,23(5)：515-519.

[10]李嗣福，刘勇．一种基于Laguerre 函数模型的预测控制算法[J]．中国科技大学学报，1999，29(3)：281-288．

[11]苗敬利,李华德,胡广大,等.感应电机最大转矩电流比的预测函数控制[J].控制与决策,2010,25(2)：218-222.

[12]吴丽娟,张宁,谢元旦.基于Laguerre级数模型的自适应动态矩阵控制[J].控制与决策,1997,12(1)：37-42.

[13]郑泽东,陈宁宁,李永东.基于模型预测控制的异步电机弱磁控制新方法[J].电工技术学报,2014,29(3)：33-40.

[14]纪科辉,沈建新.采用扰动转矩观测器的低速电机伺服系统[J].中国电机工程学报,2012,32(15)：100-106.

[15]李永东.交流电机数字控制系统[M].2版.北京：机械工业出版社, 2014.

[16]孟芳芳,邵雪卷.基于DSP感应电机预测函数控制数字实现[J].微电机,2014,47(11)：38-41.

Predictive Control of Current of PMSM Using Laguerre Model*

GAOXudong，XUMingzhu，LUANDongxue

(College of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Abstract：An adaptive predictive control method used Laguerre model was proposed. The mathematical model of the control algorithm was analyzed and optimized. The control algorithm was quantified and successfully applied in permanent magnet synchronous motor control platform based on DSP TMS280F2812. And then the prediction control results and traditional PI control results are compared. Experimental results showed that the proposed predictive control algorithm makes the PMSM has better dynamic response and steady state performance, and the engineering application value was higher.

Key words：Laguerre model； model predictive control (MPC)； current control； rolling optimization

*基金项目：国家自然科学基金面上项目(11372198)；河北省教育厅科学技术重点项目(Z9900451)

作者简介：高旭东(1990—)，男，硕士研究生，研究方向为机电系统控制及自动化。 许鸣珠(1967—)，女，博士，教授，研究方向为控制理论与应用，信号检测处理等。 栾东雪(1988—)，女，硕士研究生，研究方向为电机控制。

中图分类号：TM 341

文献标志码：A

文章编号：1673-6540(2016)05- 0012- 05

收稿日期：2015-10-26