基于单周期控制的LCL并网逆变器控制策略研究*

杨旭红，何超杰

(上海市电站自动化重点实验室，上海电力学院 自动化工程学院，上海200090)

基于单周期控制的LCL并网逆变器控制策略研究*

杨旭红，何超杰

(上海市电站自动化重点实验室，上海电力学院 自动化工程学院，上海200090)

摘要：采用单周期数字控制技术以提高LCL型并网逆变器对电压源侧输入扰动的抑制能力和系统的动态响应，以电容电流反馈作为内环、入网电流反馈作为外环的双闭环反馈控制为系统的主要结构。其中，单周期控制采用双极性算法，对内环输出信号进行逆变器开关管占空比的调制，内环在反馈通道使用比例控制，外环在前向通道使用比例积分控制。分析了以电容电流反馈构建的陷波器抑制LCL谐振的原理，并设计滤波器及控制器参数。通过MATLAB/Simulink仿真平台，建立了LCL型滤波的逆变器并网模型，仿真分析证明了该策略的可行性。

关键词：单周期控制； 并网逆变器； LCL滤波器； 双闭环控制； 有源阻尼法

0引言

分布式并网发电是对太阳能、风能等可再生能源利用的主流方式，并网逆变器作为分布式电源和电网的接口，其控制技术十分关键[1-4]。逆变器控制的两个主要的目标为：(1) 逆变器输出电流与电网电压同频同相；(2) 输出的正弦波电流满足THD标准。由于逆变器开关元件工作时会产生大量谐波，必须在逆变器和电网之间加入滤波器。相比于LC型滤波器，LCL型滤波器在相同条件下对高频谐波的抑制能力更好，逐渐广泛应用于大功率、低开关频率的并网变换器设备[5]。但是，LCL型滤波器的三阶特性即在谐振频率处增益会无穷大，同时相位发生180°跳变，会导致系统发生振荡甚至不稳定[6]。因此，对LCL滤波器的参数选择和固有谐振的抑制十分重要。

对于谐振的抑制，方法之一是有源阻尼法中的以电容电流为反馈变量的陷波器校正法[7-8]。该方法只需在反馈通道配置一个比例环节，且不受系统参数影响，易于实现有源阻尼控制[9]。文献[10]提出一种电容支路电流反馈有源阻尼策略和反馈参数设计方法，并与无源阻尼法进行对比研究。文献[11]采用单周期控制实现三相整流器的控制并证明当直流源端电压恒定时单周期控制(One-Cycle Control, OCC)与正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)在本质上是一致的。但OCC兼具调制和控制双重功能，可根据控制的要求在一定范围内增加控制器的自由度[12]。其中一个应用是在分布式能源并网发电中直流端的稳压目标，可通过对OCC添加辅助控制器实现。由于OCC本身的控制特点决定了其对输入的扰动有很好的抑制效果。文献[13]提出了在αβ0坐标系下采用比例谐振控制和单周期控制实现LCL型滤波器的逆变器并网。

基于上文所述，本文采用OCC技术，作为一种非线性控制的新型PWM调制技术，对并网逆变器输入和负载扰动都有很好的抑制能力，且具有很好的动态响应。另外，在dq0坐标系下采用双闭环控制，外环采用PI控制，内环采用比例P和OCC控制，与αβ0坐标系下采用比例谐振控制相比，减少了系统的阶数，在系统的控制设计上更容易。通过理论和仿真分析，验证了该策略的可行性与正确性。

1逆变器并网的单周期控制技术

LCL型滤波器的三相逆变器并网的主电路拓扑如图1所示。

图1中，Ua、Ub、Uc为三相电网电压；Udc为直流源电压；L1、L2、C为逆变侧滤波电感、网侧滤波电感和滤波电容；i1、i2、ic为逆变侧的电感电流、并网(网侧)电流和电容电流。

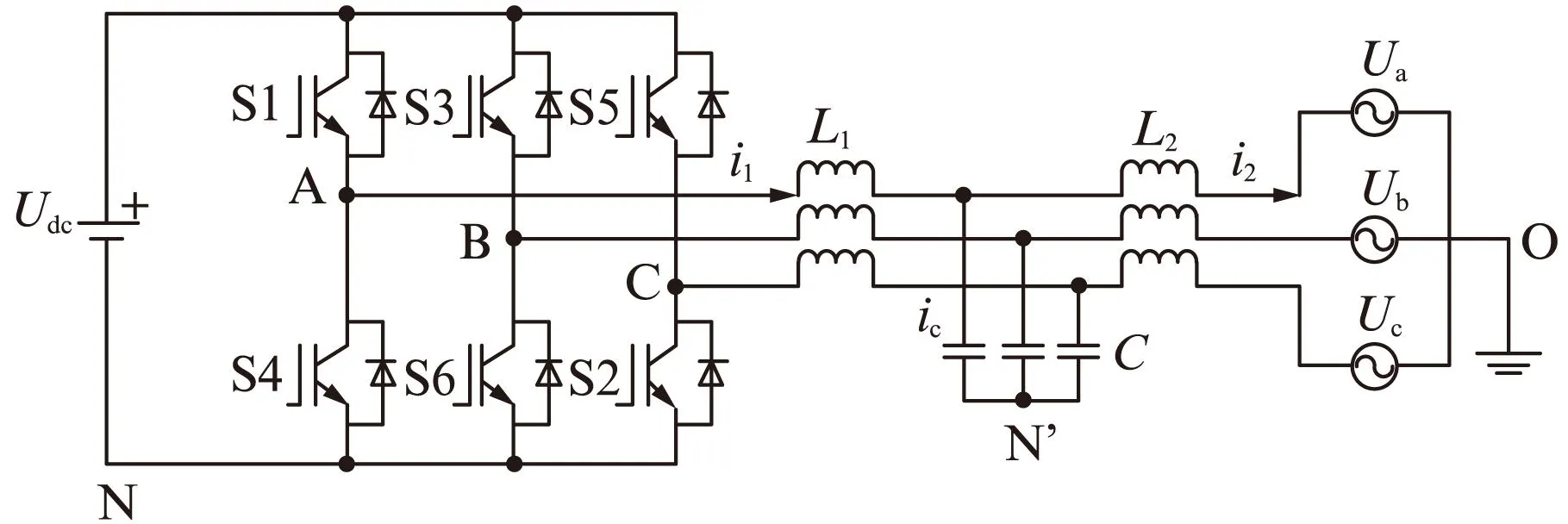
图1　LCL型滤波器三相逆变器并网拓扑

本文的控制策略主要是：以电容电流作为内环的反馈变量，以电网电流作为外环的反馈变量，在dq0坐标系下外环的控制器为PI控制器，内环采用比例P和OCC控制，内环的输出通过数字单周期控制技术实现逆变器开关管的占空比调制。由此，可以得到本文提出的控制策略的控制结构图，如图2所示。

图2　LCL型并网逆变器控制结构图

从图2可知，电容电流在dq0坐标系下反馈后经比例P调节的输出量重新反变换到三相静止坐标系下。该输出量作为参考信号经过OCC获得开关信号。

对于OCC算法的实现，首先假设逆变器的内阻抗为零、无死区时间和迟滞以及同一桥臂的上下开关管始终为互补状态[14-15]。根据图1的拓扑结构可以得式(1)：

(1)

(2)

式中：Dap、Dbp、Dcp——逆变器开关管1、3、5的占空比；

uCaN′、uCbN′、uCcN′——各相滤波电容的电压。

由于开关频率远大于电网电压频率，认为L1的电压在一个开关周期内为0。因此，可根据式(1)和式(2)推得

(3)

求解矩阵方程可知，方程的通解由齐次解和特解组成，如式(4)所示。

(4)

由于电容的电压与其电流呈正比，因此控制电容的电压可通过控制电容的电流实现，即电容电流反馈后经P控制器的输出量等同于根据电容的电压除以jωC后反馈的输出。因此，可由式(4)得到电容电流和占空比之间的关系，表达示如式(5)所示。

(5)

由式(5)可知，OCC的传递函数为GOCC(s)=K。

由于单周期控制的每个开个周期内的输出平均值都等于参考输入，由GOCC(s)=K可知，其传递函数与直流端的输入无关，这也是其对直流输入端抗干扰好的原因。

对于k的选取[16-18]，由于占空比Dmp(m=a,b,c)的范围为：0

(6)

2三相逆变器并网系统参数设计

根据三相并网系统的结构可知，逆变器输出电压uinv(s)和ic(s)的传递函数为

(7)

式中：ωres=sqrt[(L1+L2)/L1CL2]——系统的固有谐振频率。

根据式(7)和图2可求得以ic为反馈变量的基于陷波器校正法的有源阻尼控制框图，如图3所示。

图3　双闭环电流控制系统框图

图3中，k1为比例P控制的参数，G(s)为uinv(s)和i2(s)的传递函数，表达式如式(8)所示。

(8)

GPI(s)=kp+ki/s。因此，根据图3可以求得该系统的开环传递函数Gop(s)：

(9)

由式(9)可知，图3虚线框中构建的陷波器通过零极点对消在开环传递函数中已不存在谐振频率。其闭环传递函数Gcl(s)为

(10)

因此，系统的特征多项式为

(11)

根据劳斯-赫尔维茨稳定判据[20]可得系统的稳定条件

(12)

满足条件式(12)只能保证系统是稳定的，而系统的稳态和动态性能还取决于对系统的参数进行更细致的选择。对于高阶系统，可以采用主导极点的概念对其进行近似分析。对于本文所述的4阶系统，将闭环传递函数表达为

(13)

由于零点的存在会影响系统的动态性能，所以b0应在范围内尽可能大，或与某一个极点构成偶极子，但也要尽可能地远离虚轴。对于极点，则设计为两个主导的共轭极点和两个非主导的共轭极点或两个非主导的实轴上的根。将极点配置的传递函数与系统的闭环传递函数比较，得[21]

(14)

若系统的阻尼系数ξ越大，系统的剪切频率越小，转折频率越大，则系统的响应速度变快，稳态精度变差，但是系统的稳态裕度变大。因此，需在系统的稳态精度和动态性能之间折中选择。

3仿真与分析

为了验证理论分析的正确性，进行了相关的仿真分析。在MATLAB/Simulink平台上搭建了三相逆变器并网模型，仿真模型基本参数如表1所示。

表1　模型基本参数

根据上文参数设计的理论分析，再对其进行一定的微调，得到以下控制器的参数：kp=0.61，ki=88，k1=0.91，K=265.4。本文主要对单周期控制输入端的扰动抑制能力和系统的动态性能进行验证分析。因此，仿真1令系统在0.063s时增大Udc的幅值到750V；仿真2令系统在0.063s时将系统的网侧参考电流峰值从31.1A降为25A；仿真3则令系统在0.063s时同时改变Udc和网侧参考电流峰值。仿真1、2和3网侧电流A相的波形分别如图4～图6所示。

图4　仿真1网侧电流A相波形

图5　仿真2网侧电流A相波形

仿真1、2和3网侧电流A相的波形的相位差Δθ和THD变化如表2所示。

表2　仿真数据

从图4可知，系统只需要半个周期就能够到达稳定，在0.063s时直流电压的突升对网侧电流的影响很小。从图5可知，A相电流在0.063s时突然下降，只经过0.002s后便重新稳定。由表2可知，改变前THD由1.34%到改变后的1.63%，电流的下降并没有引起太大的谐波失真。从图5及表2中的相关数据可知，同时让直流电压上升和网侧电流突降，相较于仿真1和2，对系统的干扰大一点。但系统的控制效果仍很好，对于相位基本都没有偏差。根据以上仿真分析可以说明，单周期控制对于逆变并网系统直流端的扰动有很好的抑制能力而且有很好的动态性能。

5结语

双闭环的LCL型滤波器的逆变器并网控制策略已经很成熟，本文则采用电容电流内环、电网电流外环的控制方式构建了陷波器，很好地抑制了系统的固有谐振。但是，传统的PWM方式无法完全抑制直流端的扰动，对扰动的响应缓慢，需要几个周期才能稳定。单周期作为一种非线性控制策略，始终保证每个开关周期的平均输出等于参考输入，很好地抑制了直流输入端的扰动，而且具有很好的动态性能。本文通过理论分析和仿真分析验证了上述结论，表明该策略的可行性和正确性。

【参 考 文 献】

[1]赵强松,叶永强,徐国峰.分布式发电系统中并网逆变器的新型有源阻尼策略[J].电力系统自动化,2015,39(14): 140-144.

[2]王晓刚,张杰,王佳庆.LCL滤波的PWM整流器直接功率控制[J].电测与仪表,2012,49(6)：72-76.

[3]王亚维,赵晋斌,屈克庆,等.基于轴压调节的电压控制型逆变器的并网运行模式[J].电力系统自动化,2015,39(15): 110-116.

[4]王晓刚,谢运祥,张杰,等.不平衡情况下LCL型PWM整流器准直接功率控制[J].电气传动,2013,43(11): 35-39.

[5]刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3)：110-116.

[6]潘冬华,阮新波,王学华,等.增强LCL型并网逆变器对电网阻抗鲁棒性的控制参数设计[J].中国电机工程学报,2015,35(10)：2558-2566.

[7]黄挚雄,徐保友,沈玲菲,等.LCL并网逆变器新型电流双闭环控制策略研究[J].电力系统保护与控制,2012,40(17): 1-5.

[8]韩刚,蔡旭.LCL并网变流器反馈阻尼控制方法的研究[J].电力系统保护与控制,2014,42(17)：72-78.

[9]鲍陈磊,阮新波,王学华,等.基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J].中国电机工程学报,2012,32(25)：133-142.

[10]刘计龙,马伟明,肖飞,等.一种LCL滤波器有源阻尼策略与设计方法[J].电机与控制学报,2013,17(5)：22-27.

[11]杨喜军,姚苏毅,张哲民.单周期控制的三相SPWM整流器[J].电力系统及其自动化学报,2011(1)：108-113.

[12]姜晓亮,孙频东.基于单周期控制的二自由度控制器在交流调压中的应用[J].电源世界,2011(5)：21-25.

[13]LIU X D, WU J, LIU S C, et al. A current control strategy of three-phase grid-connected inverter with LCL filter based on one-cycle control[C]∥Electrical Machines and Systems (ICEMS), 2014 17th International Conference onIEEE, 2014：939-943.

[14]TANG Y, LOH P C, WANG P, et al. Improved one-cycle-control scheme for three-phase active rectifiers with input inductor-capacitor-inductor filters[J]. Power Electronics Iet, 2011, 4(5)：603-614.

[15]FANG W, WANG Z, LIU X, et al. A novel One-cycle control strategy for three-phase power converter[C]∥Industrial Electronics and Applications, 2013 8th IEEE Conference on IEEE, 2013：544-548.

[16]程林,蒋真,陈新,等.一种用于三相逆变器的新型数字单周期区间控制研究[J].电源学报,2013(2)：84-87.

[17]刘鸿鹏,王卫,吴辉.基于单周期Z源电容电压调节的并网电流控制策略[J].太阳能学报,2014,35(6): 979-984.

[18]徐健.基于单周期控制的分布式能源并网技术研究[D].北京：北京交通大学,2014.

[19]陆超,袁静.一种基于单周期数字控制的三相逆变器的研究[J].电力电子技术,2013,47(2)：70-71.

[20]徐志英,许爱国,谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J].中国电机工程学报,2009,29(27)：36-41.

[21]戴敏.微电网中基于LCL滤波器的三相并网逆变器控制策略研究[D].济南：山东大学,2012.

A Control Strategy of Grid-Connected Inverter with LCL Filter Based on One-Cycle Control*

YANGXuhong，HEChaojie

(Shanghai Key Laboratory of Power Station Automation Technology, Automatic Engineering of Shanghai University of Electric Power, Shanghai 200090, China)

Abstract：A digital one-cycle control (OCC) technology was adopted to improve the control performance of grid-connected inverter with LCL filter which could inhabit the input disturbance of voltage source and improve the system dynamic response. The dual closed-loop feedback control was implemented with the inner loop of capacitor current and the outer loop of grid-tied current. Moreover, an OCC bipolar control algorithm was analyzed and designed to modulate the duty cycle signals of the inverter switches from the inner loop output signals. Proportional (P) control at the feedback channel of the inner loop and Proportional-integral (PI) control at the forward channel of the outer loop were adopted in proposed system. The principle was analyzed mathematically that a trap filter formed by capacitor current feedback restrained LCL resonance and the parameters of filters and controllers was designed. On the basis of MATLAB/Simulink platform, a model of grid-connected inverter with LCL filter was established and the results of simulation were analyzed to verify feasibility of the strategy.

Key words：one-cycle control(OCC); grid-connected inverter; LCL filter; dual loop control; active damping method

*基金项目：国家自然科学基金项目(61203224);上海市电站自动化技术重点实验室开放课题(13DZ2273800); 上海市科技创新行动技术高新技术领域重点项目(14511101200);上海市重点科技攻关计划(上海市科委地方院校能力建设项目)(14110500700);上海自然科学基金项目(13ZR1417800)

作者简介：杨旭红(1969—)，女，教授，硕士生导师，研究方向为智能电网控制技术、新能源发电及储能技术、火电和核电机组的仿真建模及控制技术。

中图分类号：TM 464

文献标志码：A

文章编号：1673-6540(2016)05- 0007- 05

收稿日期：2015-10-26

何超杰(1990—)，男，硕士，研究方向为微电网逆变器控制技术。