基于FCM的暂态电能质量扰动识别
韩玉环,赵庆生,郭贺宏,王振起,张学军
(1.太原理工大学电力系统运行与控制山西省重点实验室,山西 太原 030024;2.国网晋中供电公司,山西 晋中 030600;3.山西大学, 山西 太原 030006)
基于FCM的暂态电能质量扰动识别
韩玉环1,赵庆生1,郭贺宏2,王振起2,张学军3
(1.太原理工大学电力系统运行与控制山西省重点实验室,山西 太原 030024;2.国网晋中供电公司,山西 晋中 030600;3.山西大学, 山西 太原 030006)
提出一种应用模糊C均值聚类(FCM)对暂态电能质量扰动进行识别的新方法。该识别方法分层实现,第一层判断信号中是否包含暂态振荡扰动,第二层判断是否包含暂态脉冲扰动,第三层判断是否包含幅值扰动及综合判断出各种复合扰动的类型。通过与集合经验模态分解(EEMD)和奇异值分解方法的结合,分层提取出有效特征量,并将其作为 FCM的输入,得到聚类中心和隶属度矩阵。最后通过计算待测样本与已知样本的聚类中心的欧氏距离实现扰动类型识别。通过仿真分析,该分层识别方法准确可行。
模糊C均值聚类算法;暂态识别;集合经验模态分解;奇异值分解;分层识别
0 引言
近几年电网成分有了新的变化。一方面,在电源侧,电网中间歇性能源装机容量增加,使得电网中的电源出力会有一定的波动性;另一方面,在负荷侧,非线性负荷的接入,这都导致电网的电能质量下降,尤其是暂态电能质量。暂态电能质量问题一般持续时间较短,发生的随机性较大,但因此产生的后果往往比较严重,且其常为复合扰动,这都导致识别困难。为改善暂态电能质量,需对暂态电能质量进行监测和分析,而对暂态电能质量扰动类型进行有效的识别是其重要前提条件[1]。
暂态扰动从性质上可分为基波电压幅值扰动和加性扰动两类[2]。基波幅值扰动包括电压暂升、暂降、中断,加性扰动有暂态振荡、暂态脉冲,其中,振荡频谱特性较明显,而脉冲暂态频谱特性不明显[3]。
暂态扰动信号的分类识别的关键是对其特征参数的提取。目前特征提取方法有:傅里叶变换、小波变换[4]、S变换[5]、HHT变换[6]等。其中,HHT变换吸取了小波变换多分辨率的优势,克服了小波变换中选取小波基的困难,从信号本身的尺度特征[7]出发对信号进行分解,也具有良好的局部适应性。用于分类的方法有神经网络[8]、决策树[9]、支持向量机[10]、专家系统[11]及贝叶斯分类器[12]等。这些方法可靠性高,但特征提取和添加分类器的过程十分复杂,因此寻找简单易行的方法进行识别是非常有必要的。
FCM聚类算法是Bezde[13]在1974年提出的一种聚类分析算法,作为早期硬C均值聚类方法的一种改进,已成功应用到模式识别、图像处理、模糊控制和基因识别等多个领域。
本文将模糊C均值聚类(FCM)应用于暂态电能质量扰动类型识别中,利用EEMD和奇异值分解方法得到信号的有效特征向量,作为FCM的输入,实现扰动类型的识别。
1 EEMD方法和奇异值分解
1.1EEMD方法
经验模态分解(EMD)[14]是一种自适应时间–频率信号分析方法,已被各领域学者成功用于处理各种问题。但是仍存在一些问题没有解决。其中比较严重的问题为易产生模态混叠[6],具体表现在:①一个单独的IMF中含有全异尺度;②相同尺度出现在不同的IMF中。
集合经验模态分解(EEMD)则是针对EMD的模态混叠问题由Huang等提出的一种信号处理的新方法,在 EMD筛分过程中给信号 ()xt添加一个高斯白噪声信号 ()wt,不同尺度的信号区域将自动映射到与背景白噪声相关的适当尺度上去,解决模态混叠问题。它不需要预先设定基函数,不仅适用于平稳信号,也适用于非平稳信号[15]。
EEMD[16]的具体分解步骤如下:
1) 对EMD试验总次数M和白噪声幅值系数进行初始化,进行EMD实验的第一次迭代。
2) 执行第g次EMD试验。
① 信号 x (t)叠加一组高斯白噪声信号 wg(t),获得一个总体信号:
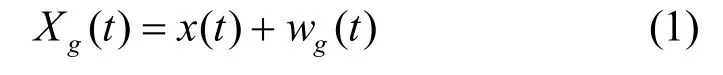
② 对 Xg(t)进行EMD分解,得到对应的IMF分量:
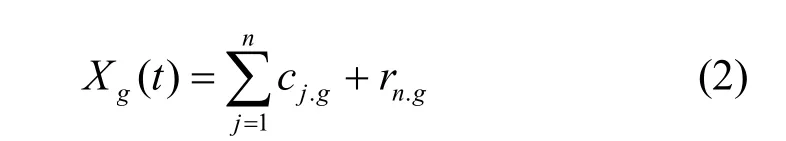
而IMF分量总个数:
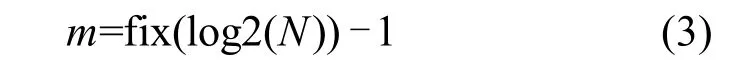
式中:N为输入信号的采样点数;fix代表向0靠拢取整。
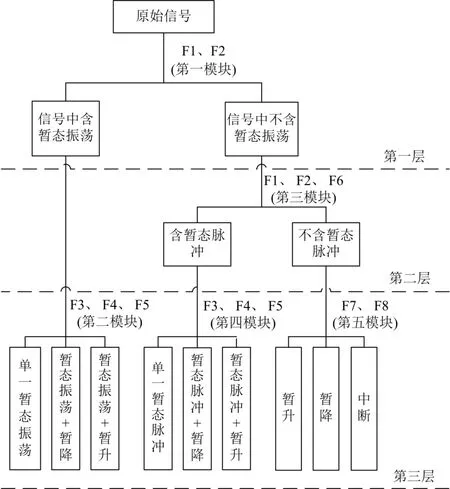
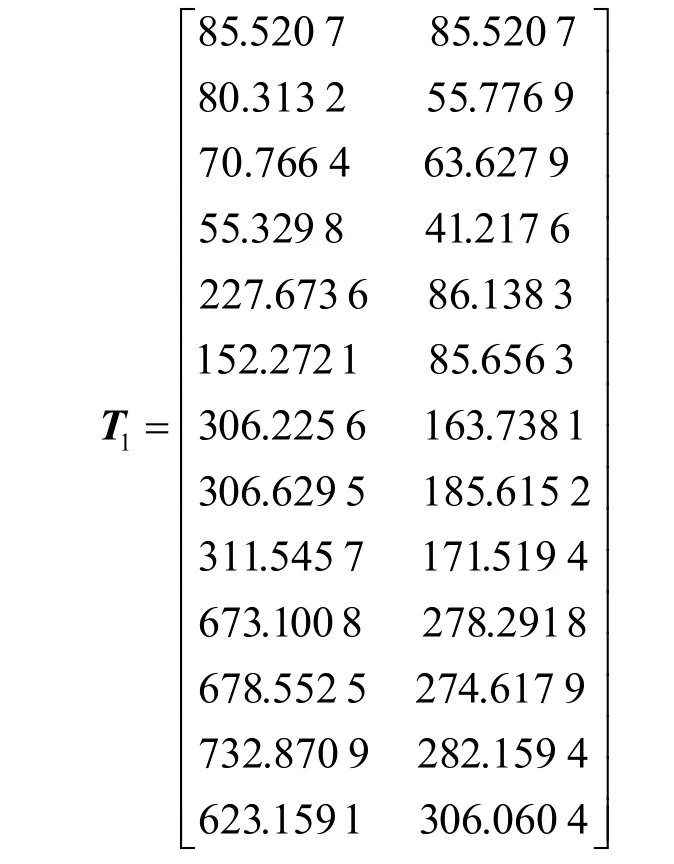
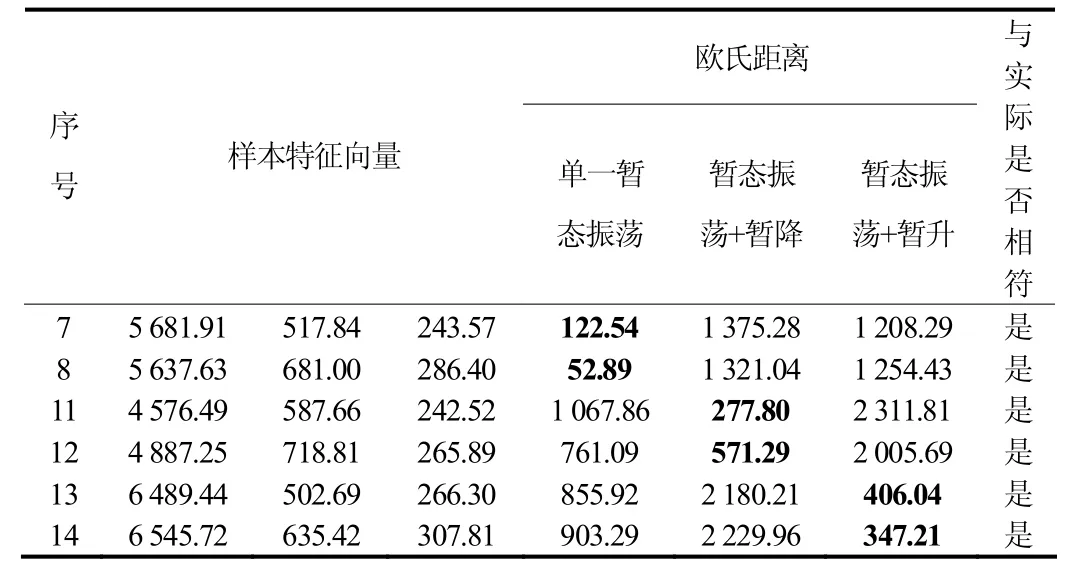
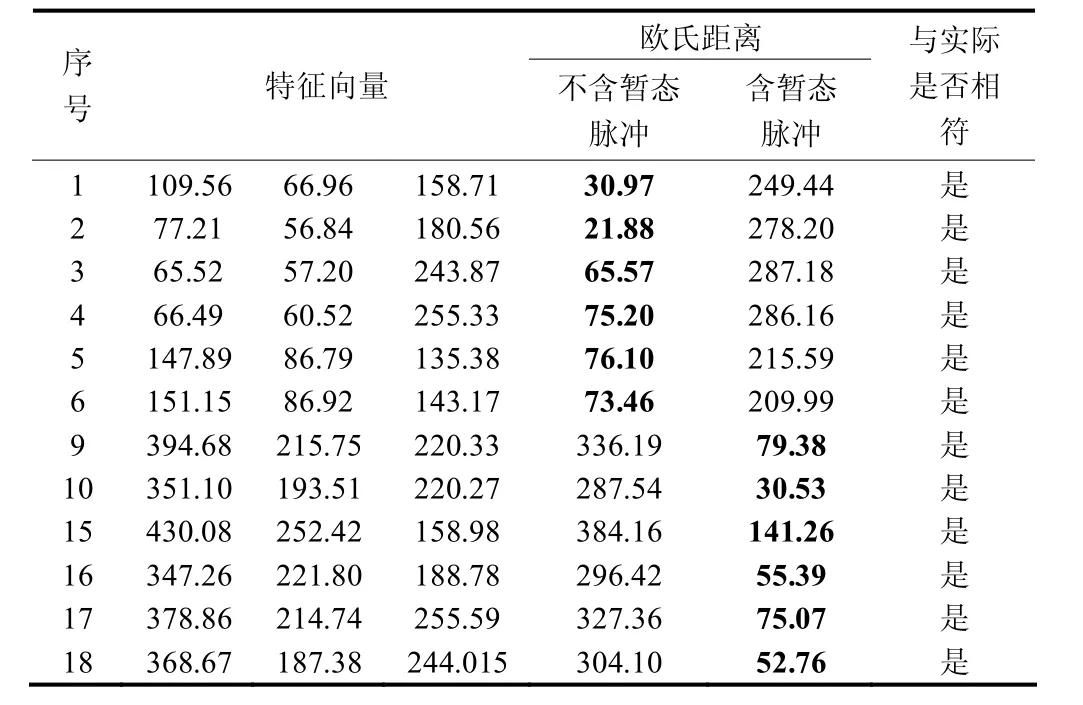
③ 判断如果g 3) 由于高斯白噪声频谱有零均值原理,可消除高斯白噪声作为时域分布参考结构带来的影响,将M次EMD试验得到的IMF分量和剩余分量进行均值计算。 1.2 奇异值分解 奇异值分解(SVD)是线性代数学中一类重要的矩阵分解,在信号处理、统计学等领域都有重要的应用。其可将包含样本特征信息的矩阵分解到不同的子空间中,是一种能够在扰动和噪声下保持信号特征相对稳定的特征量提取方法[17]。 一个m n´ 阶实矩阵A的奇异值分解定义为 模糊C均值方法是一种非监督动态聚类方法,它是通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的[18]。假定是要将样本空间分为c类,定义样本点ix属于第j(1 ≤ j ≤ c)类的程度为iju(0 ≤iju≤1),如果认为某一类样本是样本集合x上的一个模糊子集,它们所对应的隶属度矩阵就是一个模糊隶属度矩阵,用表示,元素 uij代表第i个样本属于第j类的模糊隶属度。隶属度矩阵U具有如下性质: 模糊C均值算法就是在以上三式的约束条件下对目标函数fcmJ 进行优化,即 式中:m为模糊加权指数,要求m>1; cj是所要划分的c类中第j类的中心,是样本点 xi到聚类中心 cj的欧氏距离。FCM 算法是采用迭代的方法来使目标函数最小化,其迭代过程如下: 1) 设定聚类类别数c,模糊加权数m,迭代停止阈值e,迭代次数k=0以及算法最大的迭代次数kmax,按约束条件来初始化隶属度矩阵 Uk; 2) 根据矩阵计算聚类中心[19] 3) 根据聚类中心jc更新隶属度矩阵(1)k+U ,即 3.1 暂态电能质量扰动信号模型 暂态电能质量扰动类型总体来说有单一扰动和复合扰动两类。根据文献[20]指出的复合扰动的组合原则,本论文建立了9类典型的暂态电能质量扰动信号模型,分别为电压暂降、电压暂升、电压中断、暂态脉冲、暂态振荡、暂态脉冲和暂降的复合扰动、暂态脉冲和暂升的复合扰动、暂态振荡和暂降的复合扰动以及暂态振荡与暂升的复合扰动,其参数设置依照IEEE1159标准设定。 本文是采用Matlab生成扰动样本信号,设定采样频率为 3 200 Hz,电压的基波频率为 50 Hz,扰动信号长度为25个周波。 3.2 暂态电能质量扰动识别过程 EEMD方法可对信号进行分解,得到各IMF分量,每个IMF分量只包含单一的模态,这些分量从高频到低频排成一系列。而矩阵的奇异值对于矩阵元素的扰动变化是不敏感的,具有相对稳定性,并可降低其维数。本文采用EEMD和SVD结合的方法提取特征量,用于扰动信号的分类识别。 1) F1、F2:EEMD方法分解得到的前两个固有模态分量组成的矩阵的奇异值。 2) F3、F4、F5:EEMD分解得到的前三个IMF分量组成的矩阵的奇异值。 3) F6:电压扰动信号幅值的平均值。4) F7:电压扰动信号幅值最大值与额定值的比。5) F8:电压扰动信号幅值最小值与额定值的比。基于模糊C均值聚类思想,在对各类仿真信号进行特征量提取后,分层分模块进行 FCM聚类,得到各模块的聚类中心和聚类隶属度。让待测信号的特征量与对应模块的聚类中心进行欧几里得距离判定,距离值小的代表待测信号属于该聚类中心对应的信号扰动类型,即判断出待测信号所属类别。 识别流程如图1所示。其中识别流程分为三层:第一层判断出信号是否包含暂态振荡扰动,暂态振荡的高频扰动明显,因此选择EEMD分解得到的高频分量IMF2、IMF3的奇异值F1、F2作为有效特征向量,以此作为FCM的输入,将信号聚类为含暂态振荡和不含暂态振荡两大类,得到两类的聚类中心。 图1 扰动识别原理Fig. 1 Disturbance identification schematic 第二层是在判断出信号中不含暂态振荡的基础上,判断信号中是否包含暂态脉冲。由于暂态脉冲虽与暂态振荡同属于加性扰动类中,但其频率扰动特性不明显,单以高频分量为特征不能将其与幅值扰动识别开,选择再添加幅值作为特征,因其对平均幅值的影响也不大,故易于与暂降、暂升、中断区别开。选择有效特征向量F1、F2、F6作为FCM的输入,将信号聚类为含暂态脉冲和不含暂态脉冲两大类。 第三层有三个模块组成,一个模块是在第一层判断出信号中含有暂态振荡的基础上,以特征向量F3、F4、F5作为FCM的输入,将信号聚类为单一的暂态振荡、暂态振荡和电压暂降的复合扰动、暂态振荡和电压暂升的复合扰动三大类;一个模块是在第二层判断出信号中含有暂态脉冲的基础上,以特征向量F3、F4、F5作为FCM的输入,将信号聚类为单一的暂态脉冲、暂态脉冲和电压暂降的复合扰动、暂态脉冲和电压暂升的复合扰动三大类;还有一个模块是在第二层判断出信号中不含有暂态脉冲的基础上,表明信号中只含幅值扰动,以特征向量F7、F8作为FCM的输入,将信号聚类为电压暂降、暂升、中断三大类。 4.1 函数模块实现 在Matlab平台下,对本文9类典型暂态电能质量扰动信号进行仿真,实现图1中各模块功能。 1) 第一函数模块 该模块识别出信号中是否包含暂态振荡。 在Matlab中生成13个仿真信号,其中两个电压暂降信号、两个电压暂升信号、两个电压中断信号、一个暂态脉冲信号、一个暂态脉冲和电压暂降的复合扰动信号、一个暂态脉冲和电压暂升的复合扰动信号、两个暂态振荡信号、一个暂态振荡和电压暂降的复合扰动信号以及一个暂态振荡和电压暂升的复合扰动信号。仿真信号的参数随机设置。 基于EEMD方法和SVD方法,得到各个信号的有效特征量F1、F2,组成特征量矩阵1T。 将特征量矩阵1T输入FCM中,得到其隶属度矩阵1U为 2) 第二函数模块 在确定信号中含暂态振荡后,该模块识别信号是单一的暂态振荡,还是暂态振荡和电压暂降的复合扰动,亦或是暂态振荡和电压暂升的复合扰动。 在Matlab中生成9个仿真信号,其中三个暂态振荡扰动信号,三个暂态振荡和电压暂降的复合扰动信号以及三个暂态振荡和电压暂升的复合扰动信号。仿真信号的参数随机设置。 3) 第三函数模块 在确定信号中不含暂态振荡的基础上,识别出信号是否包含暂态脉冲扰动。 在Matlab中生成12个仿真信号,其中三个电压暂降信号、两个电压暂升信号、三个电压中断信号、两个暂态脉冲信号、一个暂态脉冲和电压暂降的复合扰动信号、一个暂态脉冲和电压暂升的复合扰动信号。仿真信号的参数随机设置。 同理于第一函数模块,得到含暂态脉冲扰动的信号类型的聚类中心为不含暂态脉冲的信号类型的聚类中心为 4) 第四函数模块 确定信号中含暂态脉冲扰动后,该模块识别信号是单一的暂态脉冲,还是暂态脉冲和电压暂降的复合扰动,亦或是暂态脉冲和电压暂升的复合扰动。 在Matlab中生成9个仿真信号,其中三个暂态脉冲扰动信号,三个暂态脉冲和电压暂降的复合扰动信号以及三个暂态脉冲和电压暂升的复合扰动信号。仿真信号的参数随机设置。 5) 第五函数模块 在确定信号中不含暂态脉冲和暂态振荡的基础上,该模块识别电压暂降、电压暂升、电压中断。 在Matlab中生成10个仿真信号,其中三个电压暂降扰动信号,三个电压暂升扰动信号以及四个电压中断扰动信号。仿真信号的参数随机设置。 4.2 扰动识别仿真分析 为了验证该分层识别系统的可行性,对18组未知样本信号进行上述处理。下述各表中加粗部分为每个样本的最小欧氏距离,得到对应样本的分类。 1) 按照处理流程,对18组待测样本进行特征量F1、F2提取,与第一函数模块的聚类中心进行欧几里得距离判定,得到结果如表1所示。 2) 对1)步中测得的含暂态振荡的待测样本进行特征量 F3、F4、F5的提取,与第二函数模块的聚类中心进行距离判定,得到结果如表2所示。 3) 将1)步中测得的不含暂态振荡的待测样本进行特征量 F1、F2、F6的提取,与第三函数模块的聚类中心进行距离判定,得到结果如表3所示。 4) 将3)步中测得的含暂态脉冲的待测样本进行特征量 F3、F4、F5的提取,与第四函数模块的聚类中心进行距离判定,得到结果如表4所示。 5) 将3)步中测得的不含暂态脉冲的待测样本进行特征量 F7、F8的提取,与第五函数模块的聚类中心进行欧几里得距离判定,得到结果如表5所示。 表1 待测样本是否包含暂态振荡扰动的判定结果Table 1 Diagnosis results of sample under test whether include transient oscillation disturbance 表2 判定出待测样本具体是何种暂态振荡扰动Table 2 Determine the specific type of transient oscillation disturbance samples 表3 待测样本是否包含暂态脉冲扰动的判定结果Table 3 Diagnosis results of sample under test whether include transient pulse disturbance 表4 判定出待测样本具体是何种暂态脉冲扰动Table 4 Determine the specific type of transient pulse disturbance samples 表5 判定出待测样本具体是何种幅值扰动Table 5 Determine the specific type of amplitude disturbance samples 本文根据模糊 C均值聚类思想,结合 EEMD和SVD方法提取特征量,构建了暂态电能质量扰动的分层识别系统。该系统成功将 FCM应用到暂态电能质量扰动识别中,克服了以往分类器过程过于复杂、识别速度缓慢的缺点,使得识别系统原理清晰,识别速度快,准确率高。 实际电网中出现的暂态电能质量构成复杂,常伴有噪声等因素,利用本文提出的EEMD和SVD方法可以有效提取出实际信号中的扰动特征成分,使得该系统能更好地适用于实际暂态电能质量扰动信号的识别。 [1] 田振果, 傅成华, 吴浩, 等. 基于 HHT的电能质量扰动定位与分类[J]. 电力系统保护与控制, 2015, 43(16): 36-42. TIAN Zhenguo, FU Chenghua, WU Hao, et al. Power quality disturbance for location and classification based on HHT[J]. Power System Protection and Control, 2015, 43(16): 36-42. [2] 唐轶, 刘昊, 方永丽. 基于时域特征分析的电能质量扰动分类[J]. 电力系统自动化, 2008, 32(17): 50-54. TANG Yi, LIU Hao, FANG Yongli. A power quality disturbance classification method based on the analysis in time domain[J]. Automation of Electric Power Systems, 2008, 32(17): 50-54. [3] HAO Zhenghang, YAO Zhiqing, LI Shaohua, et al. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Technical Gazette, 2015, 22(1): 43-49. [4] 关维国, 姚清志, 高阳, 等. 基于db4小波的配电网暂态电能质量扰动的检测与定位[J]. 电力系统保护与控制, 2015, 43(8): 102-106. GUAN Weiguo, YAO Qingzhi, GAO Yang, et al. Transient power quality detection and location of distribution network based on db4 wavelet transform[J]. Power System Protection and Control, 2015, 43(8): 102-106. [5] BHENDE C N, MISHRA S, PANIGRAHI B K. Detection and classification of power quality disturbances using S-transform and modular neural network[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 122-128. [6] 李天云, 赵妍, 李楠, 等. 基于 HHT的电能质量检测新方法[J]. 中国电机工程学报, 2005, 25(17): 52-56. LI Tianyun, ZHAO Yan, LI Nan, et al. A new method for power quality detection based on HHT[J]. Proceedings of the CSEE, 2005, 25(17): 52-56. [7] 姚致清, 张茜, 刘喜梅. 基于PSCAD/EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制, 2010, 38(17): 76-81. YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J]. Power System Protection and Control, 2010, 38(17): 76-81. [8] 罗新, 牛海清, 来立永, 等. 粒子群优化自适应小波神经网络在带电局放信号识别中的应用[J]. 电工技术学报, 2014, 29(10): 327-333. LUO Xin, NIU Haiqing, LAI Liyong, et al. Application of adaptive wavelet neural network based on particle swarm optimization algorithm in online PD pattern recognition[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 327-333. [9] 赵凤展, 杨仁刚. 基于 S变换和时域分析的电能质量扰动识别[J]. 电网技术, 2006, 30(15): 90-94. ZHAO Fengzhan, YANG Rengang. Power quality disturbances classification based on S-transform and timedomain analysis[J]. Power System Technology, 2006, 30(15): 90-94. [10] 张瑾, 潘必超. 基于支持向量机高压静电场闪络信号的模糊识别[J]. 电网与清洁能源, 2015, 31(8): 1-5. ZHANG Jin, PAN Bichao. Fuzzy recognition for flashover signal in high voltage electrostatic field based on support vector machines[J]. Power System and Clean Energy, 2015, 31(8): 1-5. [11] 杨洪耕, 刘守亮, 肖先勇, 等. 基于S变换的电压凹陷分类专家系统[J]. 中国电机工程学报, 2007, 27(1): 98-104. YANG Honggeng, LIU Shouliang, XIAO Xianyong, et al. S-transform-based expert system for classification of voltage dips[J]. Proceedings of the CSEE, 2007, 27(1): 98-104. [12] 周雒维, 管春, 卢伟国. 多标签分类法在电能质量复合扰动分类中的应用[J]. 中国电机工程学报, 2011, 31(4): 45-50. ZHOU Luowei, GUAN Chun, LU Weiguo. Application of multi-label classification method to catagorization of multiple power quality disturbances[J]. Proceedings of the CSEE, 2011, 31(4): 45-50. [13] BEZDEK J C. Cluster validity with fuzzy sets[J]. Journal of Cybernetics, 1974, 3(3): 58-72. [14] 孙一航, 武建文, 廉世军, 等. 结合经验模态分解能量总量法的断路器振动信号特征向量提取[J]. 电工技术学报, 2014, 29(3): 228-236. SUN Yihang, WU Jianwen, LIAN Shijun, et al. Extraction of vibration signal feature vector of circuit breaker based on empirical mode decomposition amount of energy[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 228-236. [15] 王新, 孟玲玲. 基于 EEMD-LSSVM的超短期负荷预测[J]. 电力系统保护与控制, 2015, 43(1): 61-66. WANG Xin, MENG Lingling. Ultra-short-term load forecasting based on EEMD-LSSVM[J]. Power System Protection and Control, 2015, 43(1): 61-66. [16] 茆美琴, 龚文剑, 张榴晨, 等. 基于 EEMD-SVM方法的光伏电站短期出力预测[J]. 中国电机工程学报, 2013, 33(34): 17-24. MAO Meiqin, GONG Wenjian, ZHANG Liuchen, et al. Short-term photovoltaic generation forecasting based on EEMD-SVM combined method[J]. Proceedings of the CSEE, 2013, 33(34): 17-24. [17] 阮羚, 李成华, 宿磊, 等. 基于奇异值分解的局部放电模式识别方法[J]. 电工技术学报, 2015, 30(18): 223-228. RUAN Ling, LI Chenghua, SU Lei, et al. Pattern recognition for partial discharging using singular value decomposition[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 223-228. [18] 吴浩, 李群湛, 易东. 基于广域状态信息和模糊C均值聚类的电网故障区域判别[J]. 电力自动化设备, 2013, 33(7): 39-45. WU Hao, LI Qunzhan, YI Dong. Faulty region identification based on wide-area state information and fuzzy C-means clustering[J]. Electric Power Automation Equipment, 2013, 33(7): 39-45. [19] 谢静, 束洪春, 王科, 等. 基于 FCM 算法的高压开关柜局部放电状态评价方法研究[J]. 高压电器, 2015, 51(10): 82-90, 96. XIE Jing, SHU Hongchun, WANG Ke, et al. Study on state evaluation of partial discharge in high voltage switchgear based on fuzzy clustering algorithm[J]. High Voltage Apparatus, 2015, 51(10): 82-90, 96. [20] 刘志刚, 张巧革, 张杨. 电能质量复合扰动分类的研究进展[J]. 电力系统保护与控制, 2013, 41(13): 146-153. LIU Zhigang, ZHANG Qiaoge, ZHANG Yang. Review of power quality mixed disturbances identification[J]. Power System Protection and Control, 2013, 41(13): 146-153. Identification of transient power quality disturbances based on FCM HAN Yuhuan1, ZHAO Qingsheng1, GUO Hehong2, WANG Zhenqi2, ZHANG Xuejun3 A new method to identify the transient power quality disturbance based on FCM is proposed. This recognition method is implemented hierarchically. The first layer can judge whether transient oscillation disturbance is included in the signal. The second layer judges whether transient oscillation pulse is contained in the signal. The third layer judges whether the signal contains the magnitude of the disturbance and has a comprehensive judgment on the specific type of complex disturbances. Through combination with the ensemble empirical mode decomposition (EEMD) and singular value decomposition method, effective feature vectors can be extracted hierarchically, which is used as the input of FCM. In this way, the optimized classified matrix and clustering centers are obtained. Calculating the Euclidean distance between the unknown-sample samples and the known-sample ones, the disturbance type is identified. The simulation result indicates that this method is accurate and feasible. This work is supported by National Natural Science Foundation of Shanxi (No. 2015011057) and National Natural Science Foundation of China (No. 51505317). fuzzy C mean clustering arithmetic; transient identification; ensemble empirical mode decomposition; singular value decomposition; hierarchical identification 10.7667/PSPC150959 :2015-08-14 韩玉环(1990-),女,硕士研究生,主要研究方向为电能质量运行与控制;E-mail: xiaohuankaka@163.com (编辑 魏小丽) 山西省自然科学基金项目(2015011057);国家自然科学青年基金项目(51505317) 赵庆生(1969-),男,通信作者,博士,副教授,主要研究方向为电力系统运行与控制和电力系统建模与仿真。E-mail: zhaoqs1996@163.com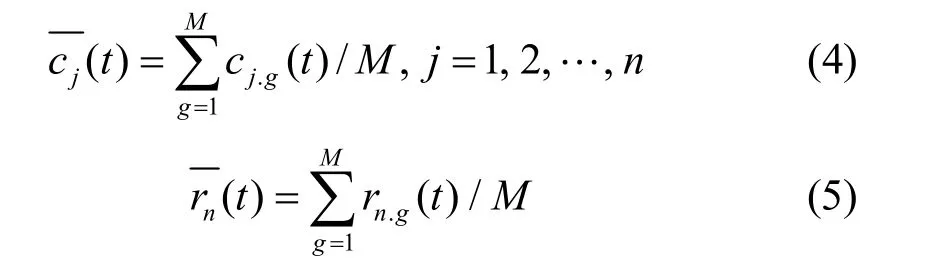

2 模糊C均值聚类(FCM)算法
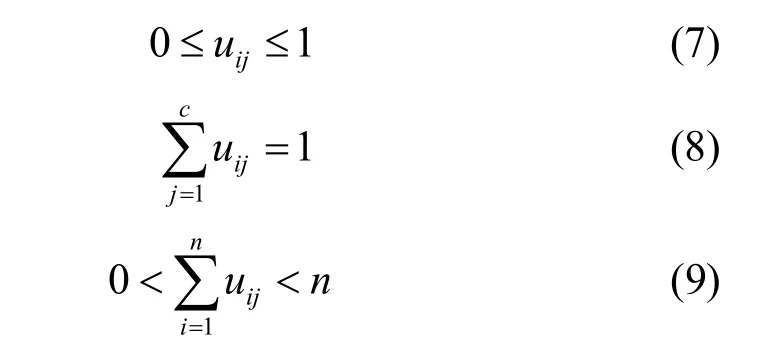
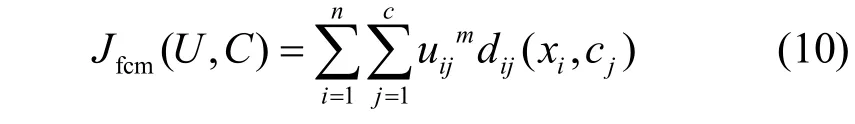
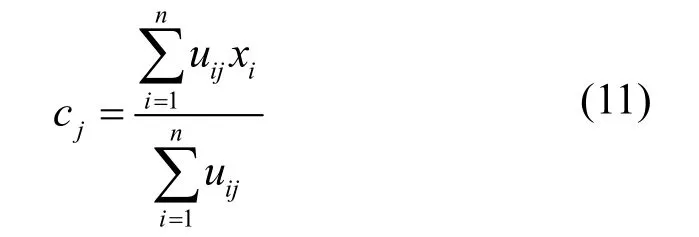
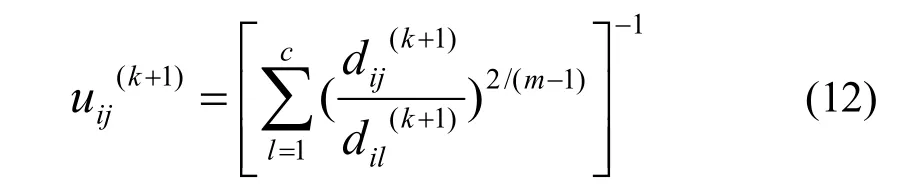
3 暂态电能质量扰动识别
4 仿真分析



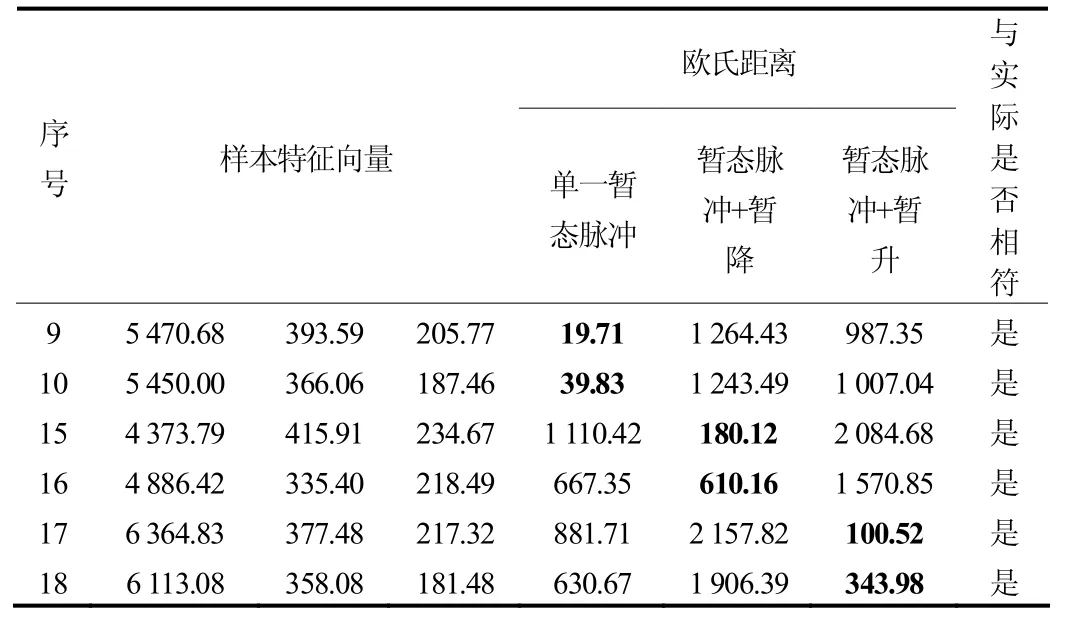
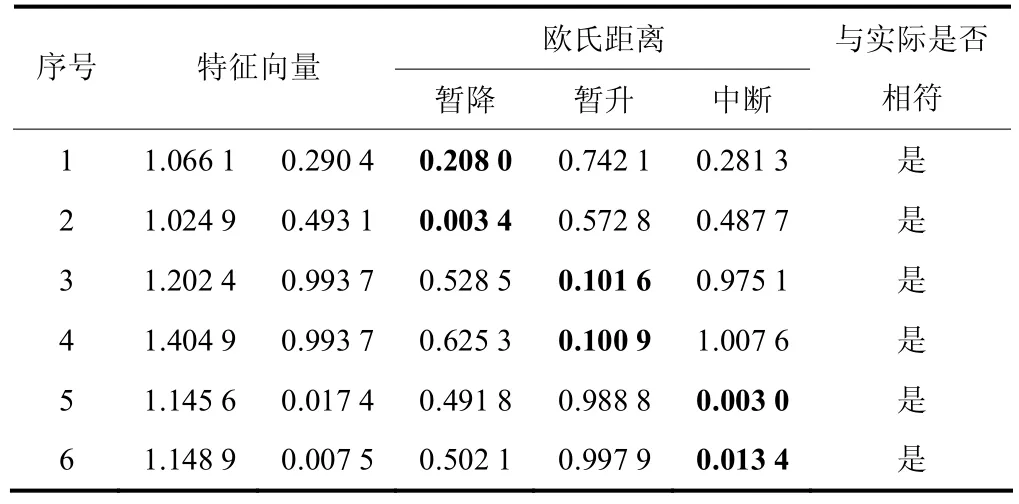
5 结论
(1. Shanxi Key Laboratory of Power System Operation and Control, Taiyuan University of Technology , Taiyuan 030024, China; 2. Jinzhong Electric Power Company, Jinzhong 030600, China; 3. Shanxi University, Taiyuan 030006, China)

