基于动态拉力与倾角的输电线路覆冰过程辨识与建模

张松海，施心陵，李 鹏,2，李孙寸，蒋建波，董吉开，张国英，李柯润

(1.云南大学信息学院，云南 昆明 650500；2.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

基于动态拉力与倾角的输电线路覆冰过程辨识与建模

张松海1，施心陵1，李 鹏1,2，李孙寸1，蒋建波1，董吉开1，张国英1，李柯润1

(1.云南大学信息学院，云南 昆明 650500；2.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

输电线路覆冰会严重影响电网的安全稳定运行，因此准确地监测线路覆冰情况对电力系统的安全运行具有重要作用。针对目前基于动态拉力与倾角的架空输电线路覆冰力学模型对现场线路覆冰的监测还有一定误差，提出了以导线动态拉力、倾角为输入，等值覆冰厚度为输出的多输入单输出耐张塔覆冰监测模型。采用系统辨识的方法，利用便于工程实践的Matlab系统辨识工具箱辨识与建模出最终模型。研究表明，最终辨识得到的模型满足实际现场情况，能准确地监测输电线路的覆冰过程情况，并为线路覆冰监测提出了一种新思路。

线路覆冰；系统辨识；耐张塔；系统辨识工具箱；监测模型

0 引言

线路覆冰容易引发断线倒塔事故、电力系统元件故障，严重威胁电网的安全运行，并造成巨大的经济损失[1-2]。目前，国内外对于线路覆冰监测做了大量的研究，并取得了显著的效果[3-4]。线路覆冰过程是受温度、湿度、冷暖空气对流、风、微气候等因素决定的综合物理现象[5-6]。因此，仅仅基于热力学理论、流体力学理论的数学模型很难全面描述线路的覆冰过程。对于架空输电线路力学模型的覆冰监测，通过测量拉力与倾角去获得导线冰荷载，进而计算覆冰质量和估算覆冰厚度[7-11]，计算过程中对模型参数的处理会大大影响结果的精度且计算复杂。架空输电线路实际覆冰是具有不同断面形状与厚度一般不均匀，为简化模型，方便计算，模型通常将实际覆冰折算成具有相同截面、厚度均匀的圆柱形覆冰[7-11]。

本文分析了基于导线动态拉力、倾角的等值覆冰厚度力学模型，在此基础上提出了以导线动态拉力、倾角为输入，等值覆冰厚度为输出的多输入单输出监测模型。利用系统辨识的方法，辨识出监测模型的未知参数，得到具体模型。由于在辨识的过程中对于确定模型的阶次和噪声模型的计算量和编程量大，为有效降低辨识工作量，方便工程计算，利用Matlab系统辨识工具箱进行辨识建模。研究表明，最终所得模型满足实际现场情况，能很好地监测线路的覆冰过程。

1 等值覆冰厚度力学模型

目前悬链线理论是对输电线路导线计算的一种精确理论。但由其计算比较繁杂，在满足工程允许的范围内，实际计算过程中一般采用悬链线理论的近似式，抛物线理论计算。利用抛物线理论预测输电线路覆冰过程，一般将输电线路导线视为理想柔索，导线不承受弯矩和压力，只承受拉力的作用。常假设架空导线比载沿线长均匀分布，覆冰密度为0.9 g/mm3，杆塔结构、线路长度不受覆冰厚度的影响而变化[8]。

输电线路在覆冰情况下，导线所受载荷是导线自重、冰重、风压等荷载的综合作用。在不考虑风偏的条件下，耐张塔档距内导线的受力分析如图1(b)所示[9]。

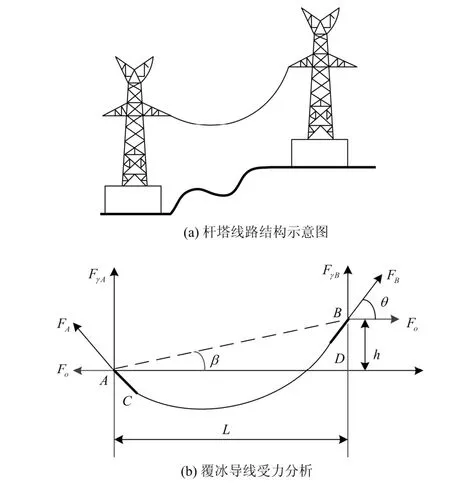
图1 线路结构及导线覆冰受力分析Fig. 1 Power transmission line structure and its icing force analysis

图1 中， A ,B为两个不等高的悬挂点，CD为输电线路导线，AC、 D B为绝缘子串。 FA、 FB分别为悬挂点 A ,B的轴向应力(N/mm2)， Fo为水平应力(N/mm2)，FγA、 FγB分别为 FA、 FB在竖直方向上的分量(N/mm2)，γa、 γb分别为悬挂点 A ,B处绝缘子串重力载荷作用在导线上的比载(N/m×mm2)，iγ为架空线路冰重比载(N/m×mm2),cγ为架空线路自重比载(N/m×mm2)，abλ λ、 为悬挂点 ,AB处绝缘子串的长度(m)，h为两个悬挂点的高度差(m)，L为两悬挂点的水平档距(m)，β为高差角，q为悬垂角，即导线轴向与水平线之间的夹角。

在竖直平面内，对悬挂点B取力矩，由力矩平衡方程可以得到：

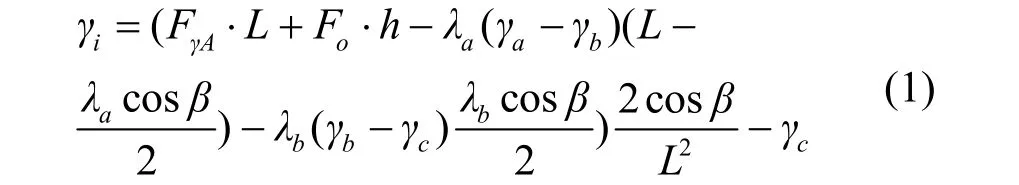
在竖直平面内，对悬挂点A取力矩，由力矩平衡方程可以得到：

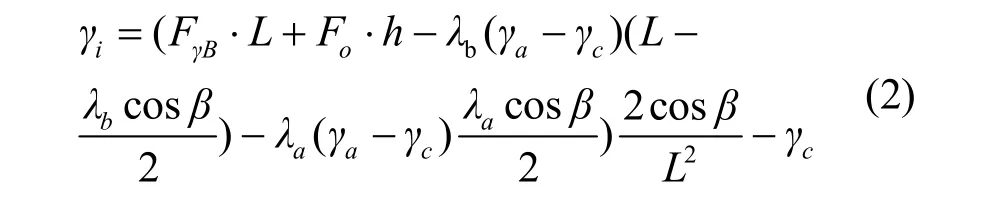
如果已知任一悬挂点的轴向应力和悬垂角，将式(3)、式(4)代入式(1)或者式(2)就可以计算出iγ。

其中轴向拉力F和悬垂角q可由拉力传感器和角度传感器分别测出。

设gice为沿架空线单位长度的覆冰重力(N/m)。

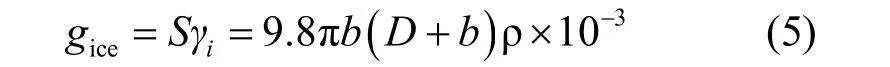
其中：S为导线截面积(mm2)；b为覆冰厚度(mm)；D为导线直径(mm)；ρ为标准覆冰密度(0.9 g/mm3)。则可以得到：

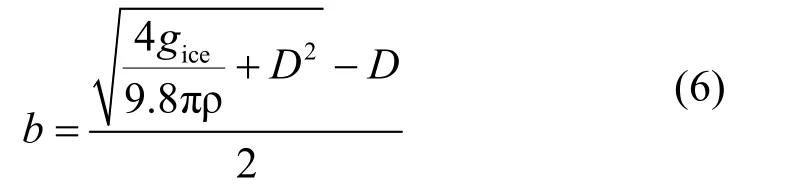
考虑风偏影响时，线路载荷将会受到水平风压荷载的影响。其中风偏角η可由传感测得。但当有风偏时，输电线路受力分析就得转化到风偏平面内，此时风偏平面内的档距ηL，高差ηh和高差角ηβ都相对于竖直平面内有所变化，其中ηθ为换算后风偏平面内的悬垂角，θ为风偏平面内的悬垂角在竖直平面的投影角，可由角度传感器测得。

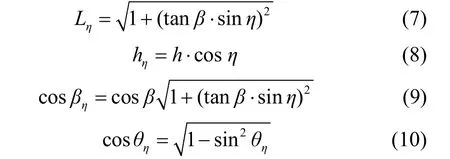
将式(7)~式(10)代入竖直平面内的等值冰厚计算公式，即可以得到风偏平面内的等值冰厚。

由上分析可知，基于动态拉力和倾角的覆冰厚度监测力学模型，综合利用拉力、导线和绝缘子倾角等参数且考虑风偏影响，模型能较好地监测覆冰厚度。同时模型也揭示出导线动态拉力、倾角与覆冰厚度呈线性关系。但由于工程计算中采用的抛物线模型是近似模型，且参数的选取是理想值，同时不考虑覆冰过程对杆塔、导线的影响，从而导致最后监测结果与实测值的误差大。

本文直接采用实测的拉力、倾角、覆冰厚度数据，利用系统辨识的方法，建立以导线动态拉力、倾角为输入，等值覆冰厚度为输出的多输入单输出监测模型。因模型的建立是直接利用现场数据辨识建模得到的，所以最终辨识得到的模型满足实际现场情况。

2 输电线路覆冰过程辨识建模

系统辨识技术广泛应用于工程和非工程的许多领域。对于复杂模型，往往不能用理论分析方法获得数学模型。凡是需要通过实验数据确定数学模型和估计参数的场合都要利用系统辨识技术。覆冰过程就是一个复杂的过程，实际工程中很难全面获得其数学模型。因此，本文通过实测的导线动态拉力、倾角和覆冰厚度数据，利用系统辨识的方法，辨识建模出覆冰过程模型。由于在辨识的过程中对于确定模型的阶次和噪声模型的计算量和编程量大，为有效降低辨识工作量，采用Matlab系统辨识工具箱进行辨识建模。本文所选的实验数据来自于文献[9]。

使用系统辨识工具箱进行辨识建模的步骤如图2所示[12-14]。

图2 系统辨识步骤Fig. 2 System identification steps

若所得模型不理想，则重复步骤：选择模型结构、估计参数、模型检验，直到得到所需的模型。

在对基于线路拉力与倾角的输电线路覆冰过程进行分析的基础上，结合实际的覆冰过程，得到如图3所示的待辨识的黑框模型。

(1) 获取观测数据

系统辨识的要求是模型结构合理，输入信号持续激励，数据量充足。将待辨识数据读入Matlab工作空间后，利用iddata函数转化为系统辨识工具箱数据对象，打开系统辨识工具箱，将iddata数据对象导入数据视图(Data Views)，如图4所示。

图3 覆冰过程辨识黑框模型Fig. 3 Black box identification model of power transmission line icing

图4 获取观测数据Fig. 4 Data collection

(2) 数据预处理

系统辨识时，要求输入、输出数据的统计特性与统计时间起点无关，且均值为 0。而实际测量得到的数据是随机时间序列，需要进行数据的去均值和重采样处理的预处理过程。

(3) 选择模型结构

如图(3)所示的黑框模型为多输入单输出的线性黑框模型，因此该模型的结构如式(11)所示[12]。

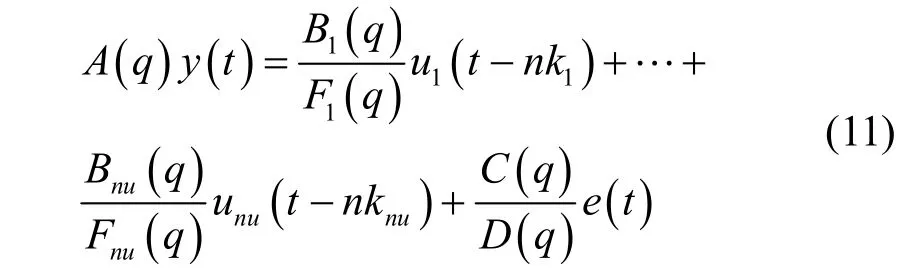
式中： y (t)为输出； u1(t- n k1)、 unu(t- n knu)分别为第1个和第nu个输入； n knu为第nu个输入的延迟参数量；e ( t)为白噪声； A 、B 、 C 、 D 、 F为待辨识的参数向量。

(4) 参数辨识

式(11)所示的模型结构在系统辨识工具箱中没有辨识选项，利用基于预测误差法的通用线性输入输出模型pem函数，通过逐步调整阶次与延时，使得最终的预测误差(FPE)和均方差误差(MSE)达到满意之后，得到最终的系统模型。因线路覆冰系统为三输入单输出系统，因此需要辨识得到 A 、 B1、F1、 B2、 F2、 B3、 F3、C 、D 的参数值。

(5) 模型验证

将辨识出的模型导入工具箱 GUI模型的视图区(Model Views)，如图5所示。

图5 模型检验Fig. 5 Model testing

系统辨识工具箱提供了多种的模型验证方法，本实验采用预测输出来检验。将检验的数据从数据视图拖入检验数据窗口(Viladation Data)，选中辨识出的模型，模型的视图区(Model Views)的模型输出(Model Output)。工具箱会同时画出模型输出和检验数据的图形。

3 算例分析

本文利用文献[9]所提供的数据，采用第2节的辨识过程步骤进行输电线路覆冰过程验证。辨识过程的参数设置如表1所示。

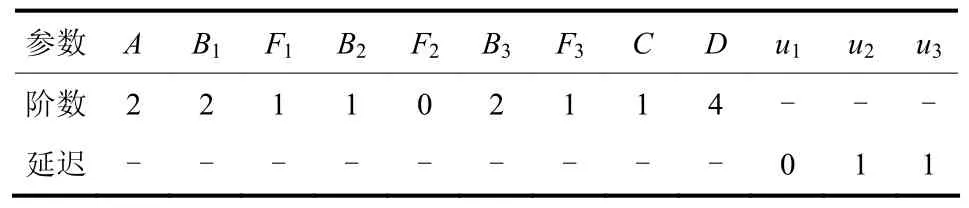
表1 辨识参数设置Table 1 Identification parameter settings

根据表1的参数设置，最终得到的模型为式(12)所示。

式中： y (k)为线路覆冰厚度； u1(k)、 u2(k- 1)、u3(k- 1)分别为线路的动态拉力、悬垂角和风偏角。

用所得到的模型在系统辨识工具箱中进行模型验证。最终结果如图6所示，图6为覆冰实际测量值、本文模型计算结果及文献[9]计算结果的比较。从图中可以看出，本文模型的计算结果与实测曲线基本吻合，且预测误差小于文献[9]的结果，即通过辨识所得系统模型能较好地反映线路拉力、倾角与覆冰厚度的关系。

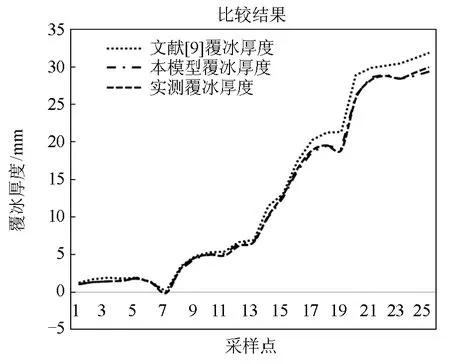
图6 系统辨识模型结果及实测数据对比Fig. 6 Comparison between models and measured data

4 结论

本文提出了基于输电线路拉力与倾角，利用系统辨识的方法对输电线路覆冰过程进行辨识建模。辨识建模过程利用Matlab系统辨识工具箱，不仅仅简化了辨识过程，而且提高了辨识精度，方便工程计算。通过辨识得到了以导线动态拉力、倾角为输入，等值覆冰厚度为输出的多输入单输出耐张塔覆冰监测模型，利用该模型进行仿真实验，结果表明本文模型比现有的输电线路覆冰力学分析监测模型更加准确，符合实际的覆冰过程。并为输电线路覆冰监测提出了一种新的思路。

[1] 段涛, 罗毅, 施琳, 等. 计及气象因素的输电线路故障概率的实时评估模型[J]. 电力系统保护与控制, 2013, 41(15): 59-67. DUAN Tao, LUO Yi, SHI Lin, et al. A real-time fault probability evaluation model of transmission line considering meteorological factors[J]. Power System Protection and Control, 2013, 41(15): 59-67.

[2] 张东飞, 马瑞, 鲁海威, 等. 冰冻灾害条件下基于气象参数连续性的配电网可靠性评估方法[J]. 电力系统保护与控制, 2013, 41(22): 51-56. ZHANG Dongfei, MA Rui, LU Haiwei, et al. A method of evaluating the distribution system reliability under freezing disaster weather based on the continuity ofmeteorological parameters[J]. Power System Protection and Control, 2013, 41(22): 51-56.

[3] 王黎明, 李海东, 梅红伟, 等. 输电线路覆冰在线监测系统国内外研究综述[J]. 高压电器, 2013, 49(6): 48-56. WANG Liming, LI Haidong, MEI Hongwei, et al. Review of on-line monitoring system of ice coating on transmission lines[J]. High Voltage Apparatus, 2013, 49(6): 48-56.

[4] 苑吉河, 蒋兴良, 易辉, 等. 输电线路导线覆冰的国内外研究现状[J]. 高电压技术, 2003, 30(1): 6-9. YUAN Jihe, JIANG Xinliang, YI Hui, et al. The present study on conductor icing of transmission lines[J]. High Voltage Engineering, 2003, 30(1): 6-9.

[5] 朱斌, 潘玲玲, 邹扬, 等. 考虑融冰因素的输电线路覆冰故障概率计算[J]. 电力系统保护与控制, 2015, 43(10): 79-84. ZHU Bin, PAN Lingling, ZOU Yang, et al. Fault probability calculation of transmission line considering ice melting factors[J]. Power System Protection and Control, 2015, 43(15): 79-84.

[6] ZHOU C, LIU Y B. Analytical model of high-voltage transmission line subjected to the downburst wind with rainfall[J]. Advances in Mechanical Engineering, 2015, 7(3): 1-5.

[7] 黄宵宁, 许瑞, 许家浩. 南方山区线路覆冰在线监测数据特征分析与预测模型研究[J]. 电力系统保护与控制, 2015, 43(23): 111-116. HUANG Xiaoning, XU Rui, XU Jiahao. Analysis of the characteristics for on-line monitoring data and research of the forecast model of the line icing in southern mountain area[J]. Power System Protection and Control, 2015, 43(23): 111-116.

[8] 黄文焘, 邰能灵, 范春菊. 基于杆塔结构力学测量的线路覆冰在线监测系统研究[J]. 电力系统保护与控制, 2012, 40(24): 71-75. HUANG Wentao, TAI Nengling, FAN Chunju. Study on icing monitoring system of different tower overhead transmission lines based on mechanics measurements[J]. Power System Protection and Control, 2012, 40(24): 71-75.

[9] 常恒. 基于动态拉力和倾角的输电线路覆冰预测与试验研究[D]. 重庆: 重庆大学, 2013. CHANG Heng. Prediction and experimental study on ice thickness of overhead transmission line based on dynamic tension and angle[D]. Chongqing: Chongqing University, 2013.

[10] FU Ping, FARZANEH M. Simulation of the ice accretion process on a transmission line cable with differential twisting[J]. Canadian Journal of Civil Engineering, 2007, 34(2): 147-155.

[11] 黄新波, 孙钦东, 程荣贵, 等. 导线覆冰的力学分析与覆冰在线监测系统[J]. 电力系统自动化, 2007, 31(14): 89-101. HUANG Xinbo, SUN Qindong, CHENG Ronggui, et al. Mechanical analysis transmission line conductor icing and application of on-line monitoring system[J]. Automation of Electric Power Systems, 2007, 31(14): 89-101.

[12] 刘兆田, 李敬敬, 何旭, 等. Matlab系统辨识工具箱在煤泥浮选过程辨识建模中的应用[J]. 选煤技术, 2014(6): 77-80. LIU Zhaotian, LI Jingjing, HE Xu, et al. Application of Matlab system identification Toolbox to identification and modeling of the coal flotation process[J]. Coal Preparation Technology, 2014(6): 77-80.

[13] 陈岚峰, 张亚琴, 程立英, 等. 基于数据的 MATLAB系统辨识工具箱模型识别[J]. 沈阳师范大学学报(自然科学版), 2013, 31(4): 527-530. CHEN Lanfeng, ZHANG Yaqin, CHENG Liying, et al. Model identification of data based MATLAB system identification[J]. Journal of Shenyang Normal University (Natural Science), 2013, 31(4): 527-530.

[14] 齐晓慧, 田庆民, 董海瑞, 等. 基于Matlab系统辨识工具箱的系统建模[J]. 兵工自动化, 2006, 25(10): 88-90. QI Xiaohui, TIAN Qingmin, DONG Hairui, et al. System modeling based on system identification toolbox in Matlab[J]. Exploitation and Application of Software, 2006, 25(10): 88-90.

(编辑 周金梅)

Identification and modeling of the power transmission line icing based on dynamic data of tension and angle

ZHANG Songhai1, SHI Xinling1, LI Peng1,2, LI Suncun1, JIANG Jianbo1, DONG Jikai1, ZHANG Guoying1, LI Kerun1
(1. School of Information Science and Engineering, Yunnan University, Kunming 650500, China; 2. Electric Power Research Institute, Yunnan Power Research & Test Institute (Group) Corp, Kunming 650217, China)

Power transmission line icing has harmful effects to the safety and stability of power grids, so monitoring the icing process is very important for power grids system operation. At present, the icing process mechanical model based on dynamic data of tension and angle has some errors when it is actually applied in monitoring system. According to this problem, this paper proposes an icing monitoring model of strain tower with multiple input and single output. It uses dynamic tension and angle data as the input, and the equivalent icing thickness as output. In order to identify the final model and calculate conveniently, the traditional system identification method is used by Matlab System Identification Toolbox. Simulation results show that the final icing model is able to estimate the icing thickness accurately in the field condition and provides a novel method for monitoring the power transmission line.

This work is supported by National Natural Science Foundation of China (No. 61364024).

transmission line icing; system identification; strain tower; system identification toolbox; monitoring models

10.7667/PSPC151069

：2015-12-19

张松海(1991-)，男，在读研究生，研究方向为电网可靠性分析，自适应信号处理；E-mail: 470568141@qq.com

施心陵(1956-)，男，教授，博士生导师，研究方向为自适应信号处理；E-mail: xlshi@ynu.edu.cn

李 鹏(1976-)，男，博士，副教授，研究方向为输变电系统安全诊断、预警与维护决策研究。E-mail: lipeng@ ynu.edu.cn

国家自然科学基金(61364024)；云南省科技计划应用基础研究(2014FB112); 云南大学“中青骨干教师”培养计划