基于改进邻接矩阵的稀疏技术及其在电力系统计算中的应用

王小飞，胡志坚， 劼吴方 ，史梦梦，汤 鹏，邱骁奇

(1.武汉大学电气工程学院，湖北 武汉 430072；2.国网北京经济技术研究院，北京 102209；3.国网重庆市电力公司江津供电分公司，重庆 402260)

基于改进邻接矩阵的稀疏技术及其在电力系统计算中的应用

王小飞1，胡志坚1， 劼吴方2，史梦梦3，汤 鹏1，邱骁奇1

(1.武汉大学电气工程学院，湖北 武汉 430072；2.国网北京经济技术研究院，北京 102209；3.国网重庆市电力公司江津供电分公司，重庆 402260)

针对存储网络拓扑结构的邻接矩阵具有高度稀疏的特点，对其表现形式进行改进，并将改进后的邻接矩阵应用于节点优化编号、检索信息的提前确定以及节点导纳矩阵的形成。在因子分解过程中，为实现列方向的非零检索，增加了列向的存储信息，并制定相应的检索方式。根据优化编号过程中新增支路与因子分解非零注入元的关联性质，在优化编号的同时，记录新增元素的位置并形成存储框架。将所提稀疏技术应用于谐波阻抗扫描与等值程序的开发，对6个电力系统的测试结果表明，随着系统规模的增大，所提方法与传统方法及NIMSCAN程序相比，可显著提高节点方程的求解效率，适用于大规模电力系统的分析与计算。

改进邻接矩阵；稀疏技术；节点优化编号；非零注入元；电力系统计算

0 引言

随着电压等级的不断提高，新系统元件的不断出现，现代电力系统规模庞大，节点数动辄成千上万，如何有效提高其计算效率，是电力工作者非常关心的一个问题。稀疏技术[1-2]是提高计算速度的有效方法，目前，该技术已广泛应用于电力系统很多方面的分析计算中，如潮流计算[3]、暂态计算[4]、状态估计[5-6]、谐波阻抗扫描[7]等。因此结合计算机技术和电力系统的特点，对传统稀疏技术加以优化，进一步提高计算效率，对电力系统各种分析计算都有重要意义。

文献[8]研究了稀疏向量技术在电网计算中的应用；文献[9]将一个n阶矩阵用n个行向量表示，但在存取技术上并没有明显改进；文献[10-12]研究了基于链表的稀疏技术，针对因子分解中的新增非零元，文献[10]在注入元出现时增加结点，文献[11]在数组尾预留一定的空间来存放产生的注入元，文献[12]采用不完全模拟LU分解预测注入元位置。这些方法的使用有效提高了稀疏技术的性能，但仍存在两个缺点：(1) 在稀疏矩阵结构确定的情况下，数组存储比链表存储更节省内存[13]，检索效率更高[14]；(2) 节点优化编号的过程中，已产生新增非零元的信息，可提前确定因子表结构。

随着将 STL(Standard Template Library)纳入C++标准，数组的功能得到极大的完善。利用容器数组可以方便地进行插入、删除、查找等操作，且不会出现维数不足的情况，使原本对数组的复杂操作变得简单。

本文以BPA数据为基础，利用改进邻接矩阵对电力网络的拓扑结构进行存储，并使其参与电力系统计算的多个过程，如节点优化编号，检索信息的提前确定和节点导纳矩阵的形成，对传统的三角检索存储格式加以改进，记录首次迭代LU分解列方向非零元位置，实现了列方向的非零检索，形成了基于改进邻接矩阵的稀疏技术。最后，将该方法用于谐波阻抗扫描与等值程序的开发，对 2个标准IEEE系统和4个国内实际电力系统进行了计算，验证了本文方法的有效性。

1 改进的邻接矩阵及形成过程

目前我国普遍使用的潮流计算程序是电力系统分析计算软件PSD-BPA、PSASP和PSS/E，不同商业软件之间的数据可以进行转换[15-16]，利用已有数据可以方便地进行电力系统仿真和计算。在分析计算过程中，需要经常用到电网的拓扑结构，如何用数学方法有效地表示这种拓扑结构对提高计算效率意义重大。

1.1 改进的邻接矩阵

改进邻接矩阵 M 主要用来表示与某一节点相连的节点号及两节点之间的支路编号，以非接地支路两端的节点号和支路编号作为矩阵的行向量。矩阵M共有三列，前两列表示节点编号，第三列是对应的支路编号。

以IEEE 9节点系统为例，电网的拓扑结构和相应的改进邻接矩阵如图1所示。图中，系统共有9条支路，矩阵M共有9行，第一行表示节点1和节点2相连，支路编号为1，最后一行表示节点8和节点9相连节点，支路编号为9。

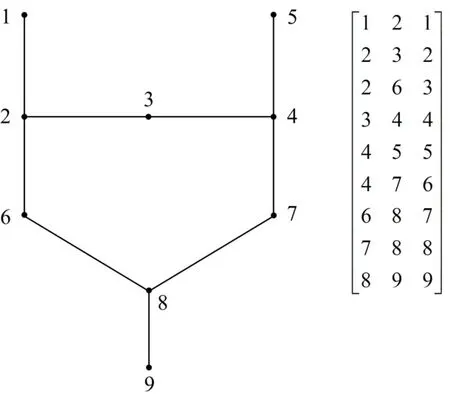
图1 IEEE 9节点系统拓扑结构和改进邻接矩阵Fig. 1 IEEE 9-bus system topology and improved adjacent matrix

1.2 形成过程

BPA数据包含了一个系统潮流计算所需的信息，其中，B卡表示母线，L卡、E卡和T卡分别表示对称线路、不对称线路和变压器支路。扫描BPA数据中的所有支路，即可得到完整的拓扑信息。

BPA数据以字符形式存储，将字符信息转换为数字信息，才能进行后续的计算。扫描BPA数据，将 B卡(母线)的节点名和节点电压存入容器数组vecB，其在 vecB中的行号就是其节点编号。将 L卡(对称线路)两侧的节点名和节点电压存入容器数组vecL。扫描vecB，找到L卡两端的节点在vecB中的位置，转化为数字后存入矩阵M，由此得到该支路的连接关系，每记录一条支路，支路编号加1。E卡、T卡处理方法与L卡相同，如此可形成完整的矩阵M。

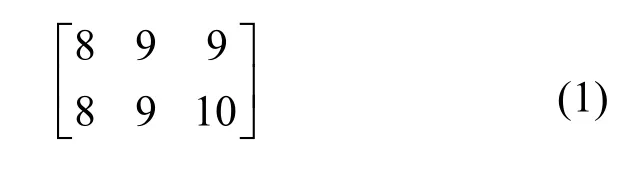
随着系统规模的增大，母线之间会出现多回输电线，根据BPA数据的特点，并不影响改进邻接矩阵的生成，矩阵M仍可表示多回输电线的情况。假设在图1节点8与9之间增加一条支路，只需在矩阵M末尾新增一行。新增后矩阵的最后两行如式(1)所示。

2 三角分解及改进的存储格式

2.1 三角分解

在电力系统计算中，需要频繁地求解线性方程组Ax=b，对于规模巨大，节点数成千上万的电力网络来说，如果不采用某种形式的稀疏技术就不可能实现。稀疏技术的关键在于排零存储和排零计算[19]，排零存储即只存储稀疏矩阵的非零元及其检索信息。排零计算即按照排零存储格式取出非零元，避免无用的零元素参与计算。

求解节点方程时，LU分解是常用的求解技术，首先对A进行LU分解，形成因子表，接着通过前代回代解出x。

令A是n阶方阵。LU分解过程如下。

(1) U的第一行元素和L的第一列元素为

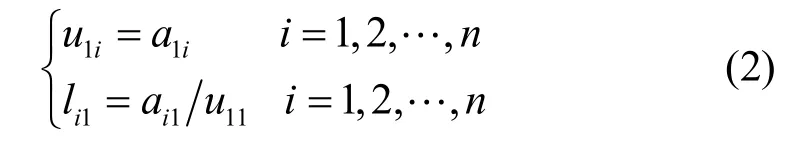
(2) 因A是对称矩阵，U的第r行元素和L的第r列元素为

(3) 前代与回代。令 =Ly b及 =Ux y，求解y与x的计算公式。

在式(2)~式(5)的计算中，只对非零元进行计算，即排零计算。

2.2 改进的存储格式

传统的三角检索存储格式无法实现列方向的非零检索，本文在此基础上作如下改进：(1) 按行顺序存储矩阵U对角元与非对角元；(2) 考虑到计算需要迭代多次，新增2个数组UA和UB，记录首次迭代式(3)列方向的非零信息；(3) LU分解第1行未用到列方向的计算，因此UB从第2行开始存储；(4) 由式(3)LU分解的对称性，只存储矩阵U及其检索信息，节约内存；(5) 为保证程序的完整性，IU、UB各增加一个元素。

各存储数组格式为

YU：按行顺序存储矩阵U上三角非零元；

JU：JU[p]存储元素YU[p]所在的列号；

IU：IU[k]存储矩阵U上三角元素中第k行第1个非零元素在YU中的位置；

UA：计算公式(3)， lrk×uki¹ 0时，存放 uki所在的行号；

UB：UB[p]存储计算YU[p]时列方向第1个非零元素在UA中的位置。

以LU分解后矩阵U为例进行说明，设

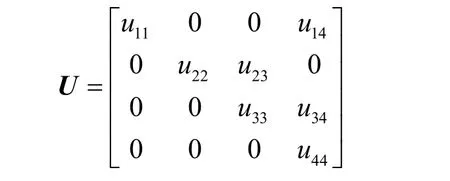
C++语言的数组下标从0开始计数，各数组存储格式如表1所示。

表1 矩阵U的存储格式Table 1 Storage format of matrix U

改进三角存储格式的优点：

(1) 增加了列方向的检索，有效提高了LU分解的效率；

(2) 按计算顺序方便地访问和引用；

(3) 利用容器数组，无需事先定义数组大小，方便地对存储信息进行修改。

图2为采用改进存储格式的LU分解流程图。

3 因子表结构及检索信息的确定

通过对LU分解过程与半动态编号过程的详细比较分析，得到与文献[20]相同的结论，即半动态编号产生的新支路就是LU分解的非零注入元。由此只需记录节点编号过程的新增支路，就可以在LU分解之前确定非零注入元的位置，提前形成存储框架及检索信息。

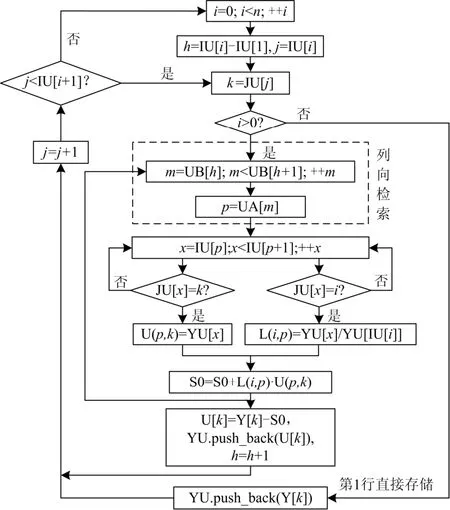
图2 改进存储格式下LU分解流程图Fig. 2 Flow chart of LU factorization using improved storage format

3.1 优化编号与因子分解的关联

半动态优化法是在节点消去的过程中，考虑节点间连接关系动态改变的情况，在每消去一个节点后立即修正剩余未消去节点的出线度，选择其中出线度最小的一个节点作为消去节点。该方法以运行时间短、编号效果好得到广泛应用，尤其是在系统规模庞大时，其优化效率要明显高于其他算法。

矩阵M包含了原始网络的拓扑信息，在编号过程中，需及时更新拓扑信息以反映拓扑结构的变化。基于M进行优化编号的具体过程如下：

(1) 去除并联支路的影响，提取矩阵M前两列互不相同的行存放到矩阵M0；

(2) 扫描矩阵M0，统计每个节点的出线度，存放到数组ND；

(3) 消去出线度最小的一个节点i；

(4) 在 M0中去掉与节点i相关的所有支路，并记录新增的支路；

(5) ND[i]=0，与节点i相连的所有未消去节点出线度减1，新增支路两端节点的出线度加1；

(6) 重复执行步骤(3)至步骤(5)，直到所有节点均被消去。

半动态法节点优化编号流程图如图3所示。

图3 半动态法节点优化编号流程图Fig. 3 Flow chart of node ordering optimization with semi-dynamic algorithm

以IEEE 9节点系统为例，半动态法优化后的节点消去顺序为新增支路数为3。消去过程中，网络拓扑的新增支路、因子分解非零注入元如图4所示。

图4 节点编号与因子分解的关联Fig. 4 Relationship between node ordering and factorization

图4 (a)反映节点编号过程拓扑结构的变化，虚线3-6，4-6，6-7是消去过程中的新增支路；图4(b)反映 LU分解非零注入元及对拓扑信息的更新，u36,u46,u67是矩阵U非零注入元，右侧改进邻接矩阵M0记录图4(a)的新增支路。比较图4(a)新增支路与图4(b)非零注入元，可以发现两者存在一一对应的关系。需要注意的是，矩阵U是按照优化编号后的顺序形成的节点导纳矩阵因子分解得到，各元素的位置与新的编号顺序对应。

3.2 检索信息的确定

节点编号完成后的矩阵M0，包含原有节点间连接关系和节点消去过程中的新增支路，由此确定存储框架和检索信息。对照节点编号后的节点顺序，通过扫描、查找等操作即可在计算前确定矩阵U的存储框架YU和检索信息JU、IU。

具体过程如图5所示。图中，数组BestTour存储了优化编号后的节点顺序。

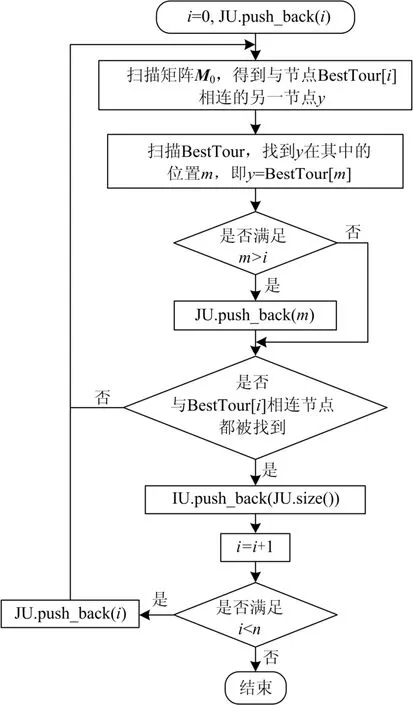
图5 确定检索信息Fig. 5 Determination of retrieval information

检索信息确定后在整个计算过程中不再发生改变，进行LU分解及前代回代时，按照数组JU、IU、UA和UB检索非零元。当产生非零注入元时，只需在数组YU的相应位置处更新注入值，整个分解过程不需要再对注入元的检索信息进行额外处理。

4 节点导纳矩阵的形成

矩阵M包含了整个网络的拓扑结构，利用矩阵M及元件的电气参数形成系统的节点导纳矩阵。具体步骤如下：

(1) k = 0，节点 i =BestTour[k ]，扫描矩阵M，得到与节点i相连的另一节点m及支路编号d；

(2) 扫描 BestTour，找到节点m的位置j，即m=BestTour[j]；

(3) 根据支路编号d判断支路类型，利用相应元件的数学模型得到节点i的部分自导纳及节点i与节点m之间的互导纳；

(4) 扫描发电机与负荷等接地元件，得到节点i的部分自导纳；

(5) 与节点i相连的所有节点都处理完毕后，形成完整一行的导纳矩阵，转步骤(6)，否则转步骤(1)；

(6) k = k+ 1，转步骤(1)，直到 k = n- 1，至此形成完整的节点导纳矩阵。

5 算例分析

计算机硬件配置：CPU为Intel Core i5，主频2.5 GHz，内存4 GB，操作系统Windows 7，开发环境Microsoft Visual Studio 2010。算例采用IEEE 162、IEEE 300标准系统与4个国内实际电力系统。

为了验证本文所提方法的快速性和有效性，对以下三种方法进行了比较。方法一：传统的稀疏技术；方法二：在本文方法的基础上不使用列方向的非零检索；方法三：基于本文方法的稀疏技术。对比了三种方法完成一次形成节点导纳矩阵、LU分解和前代回代计算的时间。三种方法所用时间如表2所示，其中，方法二加速比＝方法一计算时间/方法二计算时间，方法三加速比＝方法一计算时间/方法三计算时间。

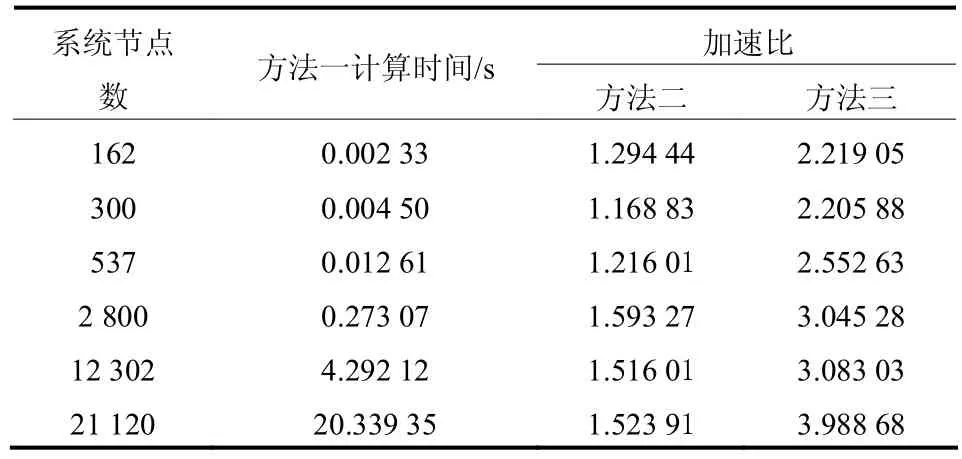
表2 三种方法完成一次计算用时对比Table 2 Comparison of the time completing one calculation between three methods

由表2可以看出，当系统规模较小时，三种方法的计算用时差别不大，但随着系统规模的增大，三者的差距越来越大，本文方法的优越性得到体现，列方向的非零检索对计算速度的提高贡献很大，在计算中应当引起重视。

将本文提出的方法应用于交流系统谐波阻抗扫描与等值程序。利用本文方法、传统稀疏技术和加拿大太西蒙公司的 NIMSCAN(Network Impedance Scanning Program)程序进行阻抗扫描，扫描频率范围50~2 500 Hz，扫描步长5 Hz。因为NIMSCAN程序只能计算母线数小于12 000的系统，故NIMSCAN只计算前4个系统。各个频次下的计算结果均在允许的误差范围之内，计算时间如表3所示，归一化后的用时对比如图6所示。

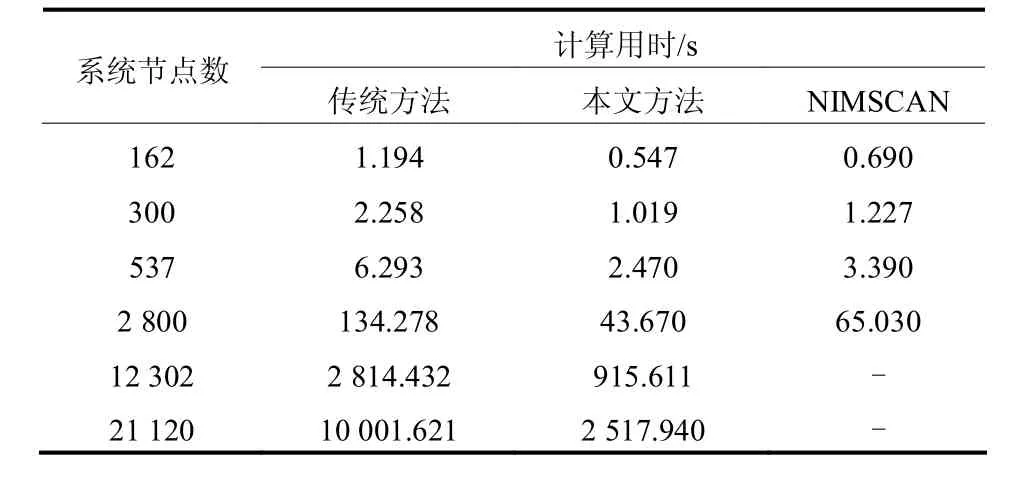
表3 三种方法计算用时对比Table 3 Comparison of the calculation time between three methods

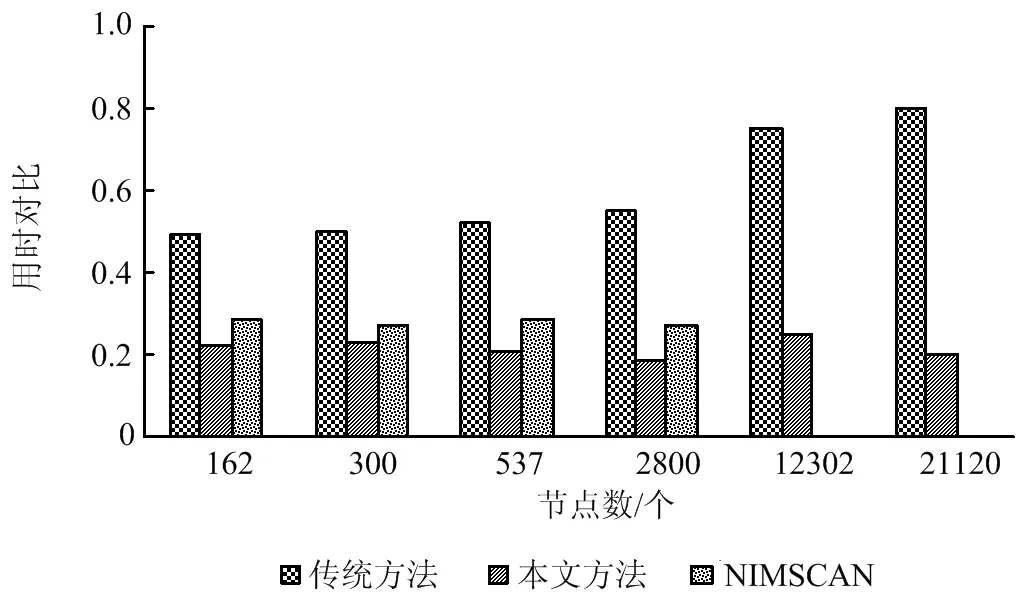
图6 归一化后计算用时对比Fig. 6 Comparison of the normalized calculation time

从表3和图6可以看出，本文提出的方法较传统的稀疏技术和NIMSCAN程序用时更短，尤其在系统规模较大时，速度提升的更多，表明了本文方法的高效性。同时，本文提出的基于改进邻接矩阵的稀疏技术，同样可应用于电力系统其他方面的计算，以提高程序的计算速度。

6 结论

(1) 通过对传统的三角检索存储格式加以改进，实现了列方向的非零检索，使计算速度提高约一倍，在计算中须加以考虑。

(2) 根据优化编号与因子分解的关联性质，提前形成检索信息，避免了对注入元的额外处理。

(3) 提出的以改进邻接矩阵存储电网拓扑，方便了对拓扑结构的调用，结合计算机技术和电力网络特点形成的稀疏技术，可以有效提高稀疏矩阵的计算效率。此外，该方法具有普适性，对电力系统其他方面的分析计算亦具有借鉴意义。

[1] TINNEY W F, BRANDWAJN V, CHAN S M. Sparse vector methods[J]. IEEE Transactions on Power Apparatus and Systems, 1985, PAS-104(2): 295-301.

[2] 张伯明. 稀疏矢量法及其在电网计算中的应用[J]. 中国电机工程学报, 1987, 7(5): 46-55. ZHANG Boming. Sparse vector method with applications to power system calculations[J]. Proceedings of the CSEE, 1987, 7(5): 46-55.

[3] 尤钟晓, 金勇, 李述茂. 十字链表在电力系统潮流计算中的应用[J]. 电力自动化设备, 1999, 19(6): 31-33. YOU Zhongxiao, JIN Yong, LI Shumao. The application of orthogonal linked list in power flow calculation[J]. Electric Power Automation Equipment, 1999, 19(6): 31-33.

[4] 江涵, 江全元. 基于GPU计算平台的大规模电力系统暂态稳定计算[J]. 电力系统保护与控制, 2013, 41(4): 13-20. JIANG Han, JIANG Quanyuan. A parallel transient stability algorithm for large-scale power system based on GPU platform[J]. Power System Protection and Control, 2013, 41(4): 13-20.

[5] 徐得超, 李亚楼, 吴中习. 稀疏技术在电力系统状态估计中的应用[J]. 电网技术, 2007, 31(8): 32-36. XU Dechao, LI Yalou, WU Zhongxi. Application of sparse techniques in power system state estimation[J]. Power System Technology, 2007, 31(8): 32-36.

[6] 黄知超, 谢霞, 王斌. 结合模糊综合评判与决策的电力系统状态估计[J]. 电力系统保护与控制, 2015, 43(7): 65-69. HUANG Zhichao, XIE Xia, WANG Bin. Power system state estimation combined with fuzzy comprehensive evaluation and decision-making[J]. Power System Protection and Control, 2015, 43(7): 65-69.

[7] 杨志栋, 李亚男, 殷威扬, 等. ±800 kV向家坝一上海特高压直流输电工程谐波阻抗等值研究[J]. 电网技术, 2007, 31(18): 1-4. YANG Zhidong, LI Yanan, YIN Weiyang, et al. Study on harmonic impedance equivalents used for AC filter design of ±800 kV UHVDC transmission project from Xiangjiaba to Shanghai[J]. Power System Technology, 2007, 31(18): 1-4.

[8] 何洋, 洪潮, 陈昆薇. 稀疏向量技术在静态安全分析中的应用[J]. 中国电机工程学报, 2003, 23(1): 41-44. HE Yang, HONG Chao, CHEN Kunwei. Study of sparsevector techniques applied to contingency analysis[J]. Proceedings of the CSEE, 2003, 23(1): 41-44.

[9] 毛安家, 郭志忠. 电力系统计算中的二维稀疏结构技术[J]. 继电器, 2001, 29(1): 19-21. MAO Anjia, GUO Zhizhong. The 2-order sparse structure in power system calculations[J]. Relay, 2001, 29(1): 19-21.

[10] 高毅, 王成山, 李继平. 改进十字链表的稀疏矩阵技术及其在电力系统仿真中的应用[J]. 电网技术, 2011, 35(5): 33-39. GAO Yi, WANG Chengshan, LI Jiping. An improved cross chain table based sparse matrix technology and its application in power system simulation[J]. Power System Technology, 2011, 35(5): 33-39.

[11] 郭庆阳, 伍叶凯, 郁惟镛. 面向对象编程中稀疏线性方程类构造研究[J]. 电力自动化设备, 2001, 21(8): 8-11. GUO Qingyang, WU Yekai, YU Weiyong. Study on class constructing of sparse matrix equations in object-oriented programming[J]. Electric Power Automation Equipment, 2001, 21(8): 8-11.

[12] 朱凌志, 安宁. 基于二维链表的稀疏矩阵在潮流计算中的应用[J]. 电网技术, 2005, 29(8): 50-55. ZHU Lingzhi, AN Ning. Application of two-dimensional chain table based sparse matrix in power flow calculation[J]. Power System Technology, 2005, 29(8): 50-55.

[13] 叶剑华, 林济铿. 牛顿法潮流计算中两种稀疏存储方式的效率研究[J]. 中国农村水利水电, 2005, 10(10): 28-31. YE Jianhua, LIN Jikeng. Study on the efficiency of two sparse storage modes for newton power flow calculation[J]. China Rural Water and Hydropower, 2005, 10(10): 28-31.

[14] AYRES M, WAIT D L, LE T, et al. Simulation of large scale, spacecraft power systems using sparse-matrix solution techniques[J]. Advances in Engineering Software, 2000, 31(8-9): 593-598.

[15] 叶青, 朱永强, 李红贤. 基于改进遗传算法电力系统仿真软件间模型参数转换研究[J]. 电力系统保护与控制, 2015, 43(9): 95-100. YE Qing, ZHU Yongqiang, LI Hongxian. Model parameter conversion between power system software based on IGA[J]. Power System Protection and Control, 2015, 43(9): 95-100.

[16] 刘庆, 张东英, 刘燕华, 等. BPA电网模型自动导入DIgSILENT的研究和开发[J]. 电力系统保护与控制, 2014, 42(16): 112-117. LIU Qing, ZHANG Dongying, LIU Yanhua, et al. Research and development of BPA grid model imported to DIgSILENT[J]. Power System Protection and Control, 2014, 42(16): 112-117.

[17] 胡运权, 郭耀煌. 运筹学教程[M]. 北京: 清华大学出版社, 2007: 233-250.

[18] 姚玉斌. 基于邻接矩阵准平方法网络拓扑分析[J]. 电力系统保护与控制, 2012, 40(6): 17-21. YAO Yubin. Determination of network topology by fast quasi-square of the adjacency matrix[J]. Power System Protection and Control, 2012, 40(6): 17-21.

[19] 张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 北京:清华大学出版社, 2007: 58-69.

[20] TINNEY W, WALKER J. Direct solutions of sparse network equations by optionally ordered triangular factorization[J]. Proceedings of the IEEE, 1967, 55(11): 1801-1809.

(编辑 姜新丽)

Improved adjacent matrix based sparse technology and its application in power system calculation

WANG Xiaofei1, HU Zhijian1, WU Fangjie2, SHI Mengmeng3, TANG Peng1, QIU Xiaoqi1
(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China; 2. State Power Economic Research Institute, Beijing 102209, China; 3. Jiangjin Power Supply Branch Company, State Grid Chongqing Electric Power Corporation, Chongqing 402260, China)

According to the highly sparse characteristics of the adjacent matrix used for the networks topology storing, its manifestation is improved, and the improved adjacent matrix is applied to node ordering optimization, determination of retrieval information in advance and the formation of node admittance matrix. During the process of factorization, to achieve the nonzero retrieving in the column direction, the stored information of the column direction is added and the corresponding retrieval method is made. According to the relationships between new added branches in node ordering and the nonzero injections in factorization, in the meantime of ordering optimization, the position of the new added elements is recorded and the storage framework is formed. The proposed sparse technology is used in the network impedance scanning and equivalence program, and testing results for six power systems show that, with the increase of system scale, the calculation efficiency of node equations with the proposed method is greatly improved compared with the traditional methods and the NIMSCAN program, and it is applicable to the analysis and calculation for large scale power system.

This work is supported by the Specialized Research Fund for Doctoral Program of Higher Education of China (No. 20110141110032).

improved adjacent matrix; sparse technology; node ordering optimization; nonzero injection element; power system calculation

10.7667/PSPC151094

：2015-07-22

王小飞(1991-)，男，硕士研究生，研究方向为电力系统优化与控制，谐波阻抗等值计算；E-mail: 849182668@ qq.com

胡志坚(1969-)，男，通信作者，博士，教授，博士生导师，研究方向为电力系统稳定分析与控制，新能源与分布式发电；E-mail: zhijian_hu@163.com

高等学校博士学科点专项科研基金项目(20110141110032)