Jacobi函数方程与Riemann ξ(s)函数零点

刘法胜

(山东科技大学 交通学院，山东 青岛 266590)

Jacobi函数方程与Riemann ξ(s)函数零点

刘法胜

(山东科技大学 交通学院，山东 青岛 266590)

摘要：利用Jacobi函数方程和Schwarz反射原理，给出Riemann zeta函数零点满足的方程，进而推得零点均落在实部为1/2的临界线上。如此，所有与Riemann猜想等价的命题和以Riemann假设作为前提条件的结论都成立。

关键词：黎曼猜想；Jacobi函数方程；反射原理

1研究背景

Riemann猜想(RH,Riemann hypothesis)源于Dirichlet级数函数：

(1.1)

其中：s=σ+it，Re(s)=σ>1。

文献[1]和[2]列出了有关Riemann猜想的重大历史事件。1737年，Euler给出了著名的乘积公式，即对所有大于1的实数s，有

(1.2)

其中，N为自然数，p为素数。Euler乘法公式建立起了Dirichlet级数函数和素数分布的密切联系，也可以说建立了自然数加法运算和素数乘积运算之间的一种联系。

1792年，Guass提出后来被称为素数定理的结论。1859年，Riemann在文献[3]中，将(1.1)解析延拓到除s=1外的整个复平面上，并提出Riemann猜想：Riemann ζ函数的所有非平凡零点都在临界线Re(s)=1/2上。

由Euler乘积公式(1.2)可以得到Riemann ζ函数在Re(s)>1的区域内没有零点。1896年，Hadamard和Poussion分别独立证明了素数定理。素数定理等价于Riemann ζ函数在Re(s)=1上没有零点。

1914年，丹麦数学家Bohr与德国数学家Landau证明了包含临界线的无论多么窄的带状区域都包含了Riemann ζ函数的几乎所有非平凡零点。同一年，英国数学家Hardy证明了Riemann ζ函数有无穷多个非平凡零点位于临界线上。

1942年，挪威数学家Selberg证明了有正百分比的非平凡零点在临界线上。Levinson在1974年证明了至少有34%的零点位于临界线上。直到1989年，美国数学家Conrey证明了至少有40%的零点位于临界线上。

RH之所以重要，其原因之一是RH有诸多重要等价命题和以其作为假设而成立的重要结论。文献[2]中给出了32个重要等价命题；李修贤[4]在学位论文“Riemann猜想与素数分布”中专门罗列了34个与Riemann猜想等价结论。RH的各种等价结论和基于RH而成立的结论使人们有理由相信RH的正确性，因而，人们更愿意称Riemann猜想为Riemann假设。

关于数值计算验证或者说试图举出反例的工作，极大促进了RH的相关研究。1932年，数学家Siegel从Riemann的手稿中获得了重大发现——计算Riemann ζ函数非平凡零点的方法,称为Riemann-Siegel公式。至1969年，350万个零点得到验证，全部位于临界线上，这无疑大大增强了数学家们对RH的信心。到2004年，Gourdon用计算机验证了Riemann ζ函数的前1013个零点都落在RH的临界线上。

Riemann猜想的提出已经过去近两个世纪，而猜想是否成立，一直未得到肯定。RH被公认为是“外行不懂，专家证明不了的世界难题”[2]。

Riemann的著名论文[3]“论小于给定数的素数分布”中已经意识到猜想是成立的。令人惋惜的是，Riemann提出RH七年后就撒手人寰。考察提出RH的原始论文[3]发现，Riemann通过Jacobi函数方程，给出了Riemann ζ函数的解析延拓表达[5]21。Edwards[6],Karatsuba[7]都有用theta级数函数和Jacobi函数方程处理Riemann ζ函数解析延拓论述。Jacobi函数方程与Riemann ζ函数关系密切，前者自变量的倒数与后者变量的共轭变量对应。Riemann原意就是要去证明RH，只是未能如愿，才以猜想的形式给出了著名的RH。倘若，Riemann当时就沿着此路给出RH的证明，或者后来人及时补上其证明，或许RH不会如此出名。RH的诸多重要等价问题和基于RH的重要结果进一步凸显了RH的重要性，而等价问题的难以证明则说明，除了Riemann当初猜想的基于Jacobi变换的思路外，恐怕还没有发现更有效的思路。

现在可以说，RH的极限情形和具体零点计算，只是增大了RH成立的可能性，将Jacobi函数方程性质和反射原理结合应用是证明RH的有效方法。

2以Theta级数表达的Riemann ζ函数解析延拓显表达

Dirichlet级数函数有多种解析延拓途径，由于解析延拓的唯一性原理，各种延拓形式上不同，本质上是等价的[5-7]。Riemann利用theta函数级数和Jacobi方程，将ζ函数解析延拓到除1之外的整个复数平面上[3，5]。

由于RH起源于Dirichlet级数函数的解析延拓，而基于theta级数表达的Riemann ζ函数解析延拓用到著名的Jacobi函数方程关系，为了本文的完整性和可读性，此处以定理形式给出该既有结果[5]。

定理1[8]

(2.1)

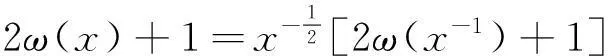
(2.2)

证明见文献[8]188页，也可参考文献[5] 5～8页给出的另一证明。

定理2[5]下述函数是Dirichlet级数函数在复平面上除s=1外的解析延拓:

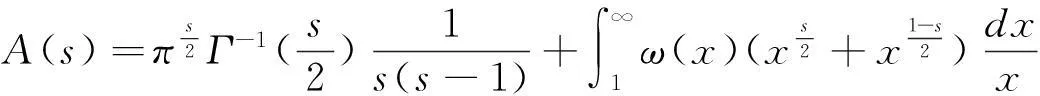
(2.3)

记A(s)=ζ(s),为Riemann ζ函数。鉴于该定理在RH中的重要性，此处给出其证明之一，详细过程见文献[5]11页。

用积分公式表示Gamma函数，对于Re(s)>0和自然数N，有

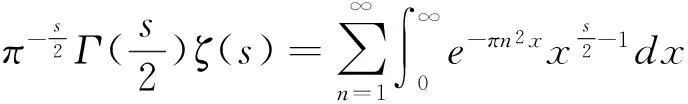
改变求和(∑)与积分(∫)的顺序(绝对收敛可以改变顺序)，则有

利用Jacobi方程(2.2)，并做积分变量x→x-1于下述第二个积分中，有

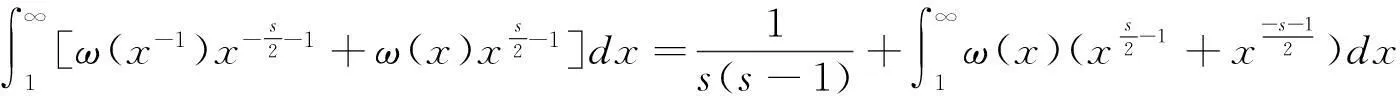
(2.4)

定理得证。

尽管对Dirichlet级数函数有多种解析延拓方法和形式，但由于解析延拓唯一性定理，它们本质上是等价的。不同的解析延拓方式会有不同的方便之处，基于theta函数级数和Jacobi方程，将Dirichlet级数函数解析延拓为上述显形式更方便。

至此，可以说，解析延拓后的Riemann ζ函数是整个复平面上除了简单极点1(其留数为1)以外所有点上的解析函数。

现在，可以在复平面上考虑Riemann ζ函数的零点了。人们对其零点感兴趣，是因为它们包含着素数的信息。然而，人们并非对Riemann ζ函数的所有零点都感兴趣，所有实部在区间[0，1]外的平凡零点被列为RH陈述之外。

在讨论其零点之前，先给出一个Riemann ζ函数的方程。注意到在A(s)中，把s与1-s作替换，等式成立。因此，有函数方程:

ξ(s)=ξ(1-s)。

(2.5)

记

(2.6)

3有关引理

为行文方便，给出以下引理[3，5]。

引理1设x是正实数，对多值对数函数只取其主枝，则

(3.1)

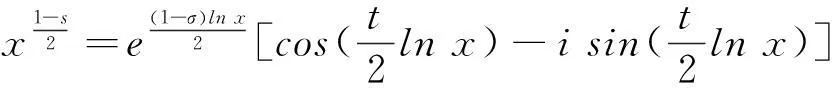
详细的证明请参考文献[5] 22页定理1。前面的等价性证明可以由式(2.6)给出；后半部分的等价性由反射原理给出，因为这里在实数轴上函数取值为实数，故由Schwarz反射定理，得引理2。

引理3设t>0，则

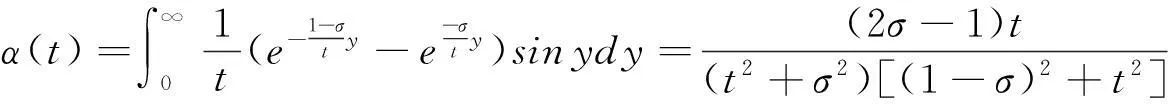
(3.2)

证明：

现在可以探讨Riemann ξ(s)函数的零点了。

4Riemann ξ(s)函数的零点

由式(2.6)，设s=σ+it为Riemann ξ(s)的零点：

(4.1)

(4.2)

(4.3)

(4.4)

由式(4.3)可得

又由引理2，-t亦满足式(4.4)

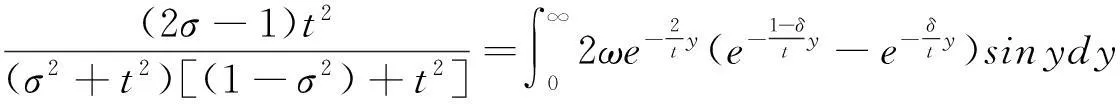
(4.5)

所以有

即

由引理3和引理4得

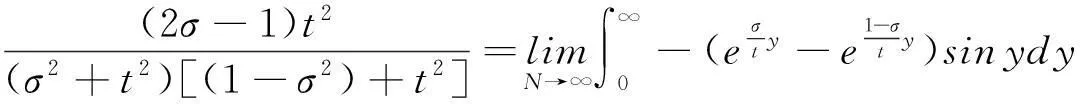
5Riemann ξ(s)函数零点计算

由式(4.2),下面函数的零点即为Riemann ξ(s)函数零点的虚部值：

(5.1)

函数(5.1)包含了全部素数分布信息，素数分布性质可以通过研究该函数的零点分布得到。

参考文献：

[1]卢昌海.黎曼猜想漫谈[M].北京:清华大学出版社,2012.

[2]BORWEIN P,CHOI S,ROONEY B.The Riemann hypothesis:A resource for the afficionado and virtuoso alike[M].New York:Springer,2008.

[3]RIEMANN B.Über die Anzahl der Primzahlen unter einer gegebenen Grösse[M]//Gesammelte Mathematische Werke Und Wissenschaftlicher Nachlass.Berlin:Monats.Preuss,1859:671-680.

[4]李修贤.黎曼猜想与素数分布[D].济南:山东大学,2012.[5]KARATSUBA A A,VORONIN S M.The Riemann zeta-function[M].Translated by KOBLITZ N.Berlin:Walter de Gruyter,1992.

[6]EDWARDS H M.Riemann’s zeta function[M].New York:Dover Publications,Inc.,1974.

[7]TITCHMARSH E C.The theory of the Riemann zeta-function[M].Oxford:Clarendon Press,1951.

[8]EVEREST G,WARD T.An introduction to number theory[M].New York:Springer,2005.

(责任编辑：吕文红)

Properties of Jacobi Functional Equation and Zeros of Riemann ξ(s)Function

LIU Fasheng

(College of Transportation,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Abstract:Using the properties of theta-series(Jacobi functional equation)and the Schwarz reflection principle,this paper presents an equation which meets the zeros of Riemann Zeta function and it is then deduced that all zeros are on the critical line where the real part is 1/2.Thus,all propositions equivalent to Riemann hypothesis and all conclusions with Riemann hypothesis as preconditions are true.

Key words:Riemann hypothesis(RH);Jacobi functional equation;reflection principle

收稿日期：2015-06-28

作者简介：刘法胜(1957—)，男，山东临朐人，教授，博士生导师，主要从事交通运输规划与管理方面的研究. E-mail：fashengliu@163.com

中图分类号：O156.4

文献标志码：A

文章编号：1672-3767(2016)01-0097-05