星形嵌段共聚物在柱状受限下自组装的相图

王超，王文锦，叶深杰

宁波大学材料科学与化学工程学院，浙江宁波315211



星形嵌段共聚物在柱状受限下自组装的相图

王超，王文锦，叶深杰

宁波大学材料科学与化学工程学院，浙江宁波315211

摘要：本文用自洽平均场理论研究了多臂星形嵌段共聚物在柱状受限下的自组装。通过计算两种位于本体自组装柱状相区（A嵌段的体积分数为0.2或0.8）的多臂星形嵌段共聚物（臂数为3、9、15或21）在柱状受限下自组装结构的相图，我们将嵌段的不对称性、星形臂的数量以及柱状受限空间的直径与自组装结构的稳定性联系起来。我们发现φA=0.8的星形嵌段共聚物能够在吸引A嵌段的孔道中自组装出一类新的穿孔层结构，这种结构随着臂数增多越来越稳定。本工作对调控嵌段共聚物的自组装有一定指导意义。

关键词：星形嵌段共聚物；自洽场理论；自组装；相图

嵌段共聚物能够在微观尺度下自组装出有序的纳米结构，例如两嵌段共聚物A-b-B本体自组装的球状相、柱状相、Gyroids相以及层状相等［1］，在光电工业、生物医药等领域有广阔的应用前景［2，3］。发掘嵌段共聚物应用价值的关键在于对其自组装结构的调控，主要有两种途径：改变嵌段共聚物本身的结构，例如分子链构型［4］；改变外部条件，例如引入几何受限［5］等。

星形聚合物分子拥有更为紧凑的结构，Xu等［6］研究了21臂星形嵌段共聚物（AB）21的本体自组装，发现星形结构对自组装有重要影响。本文同时控制分子链构型以及几何受限条件，以f臂的星形嵌段共聚物（AB）f为对象，将其限制在直径为D的柱状空间内进行自组装，用自洽场理论的方法计算了各结构的自由能，通过相图总结了臂的数量f、嵌段组分数φA以及柱状受限空间的直径D与结构稳定性之间的关系。

1　计算模型

本方法可用于各种臂数的星形嵌段共聚物在柱状受限下的自组装，我们以3臂、9臂、15臂以及21臂的星形嵌段共聚物为计算对象，以研究臂数的影响。星形嵌段共聚物（AB）f由f条臂构成，每一条臂都是两嵌段（A-b-B），通过A嵌段的自由端连接在一起，A嵌段位于星形的内部，B嵌段位于星形的外部。所有臂数的嵌段共聚物（AB）f的聚合度均为N，每一条臂的聚合度为N/f。A嵌段和B嵌段的体积分数分别为φA和φB，为了研究星形结构的影响，我们确定了φA=0.2和φA=0.8两个对称比例。ΧN为两嵌段之间的Flory-Huggins相互作用参数，两嵌段之间相互作用不在本文研究范围之内，将参数N与臂数f对应，N/f = 20。在自洽场平均场（SCFT）计算中，长度以星形高分子的回转半径Rg为单位计量，星形聚合物的均方回转半径为：

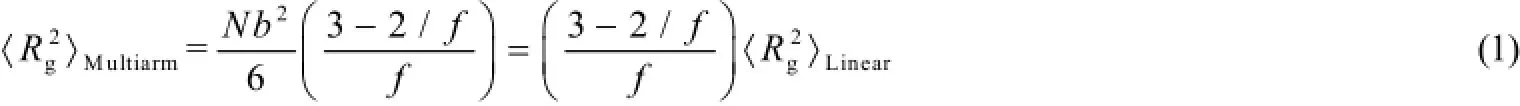
式1中b为Kuhn链长。根据多链体系Edwards理论，n条高分子链在柱状空间内自组装的自由能可以表示为：

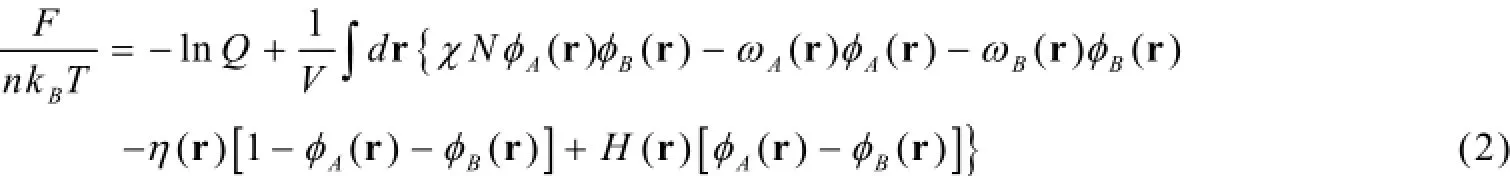
式2中，φA（r）和φB（r）分别表示A嵌段和B嵌段的浓度。将一个（AB）f分子在其他分子链作用下的状态，表示为在平均场φA和φB作用下的单链配分函数Q。与本体自组装不同，我们引入算符H（r）来表示孔道内壁对不同嵌段的不同亲和性：

只有当链节位置r在范围R-σ≤|r|≤R时，孔道内壁才对链节有吸引作用，强度V0= 0.2，超出范围则相互作用强度参数V0= 0，表示孔道内壁的吸引性对A嵌段和B嵌段不再有影响。其中，σ表示孔道内壁的作用长度，σ= 0.5 Rg，从孔道内壁出发厚度为0.5 Rg的空间范围内所有链节都会受到孔道内壁的作用；λ表示这一作用的衰减长度，λ= 0.5 Rg。作用强度参数V0＞0表示孔道内壁吸引B嵌段，作用强度参数V0＜0表示孔道内壁吸引A嵌段。我们将φA=0.2以及φA=0.8的嵌段共聚物分别限制在吸引B嵌段的孔道以及吸引A嵌段的孔道中进行自组装，保证孔道的选择性条件与嵌段比例的对称性一致。

根据体系的自由能（式2）可以确定体系的场强以及链节密度，写出自洽场方程组：

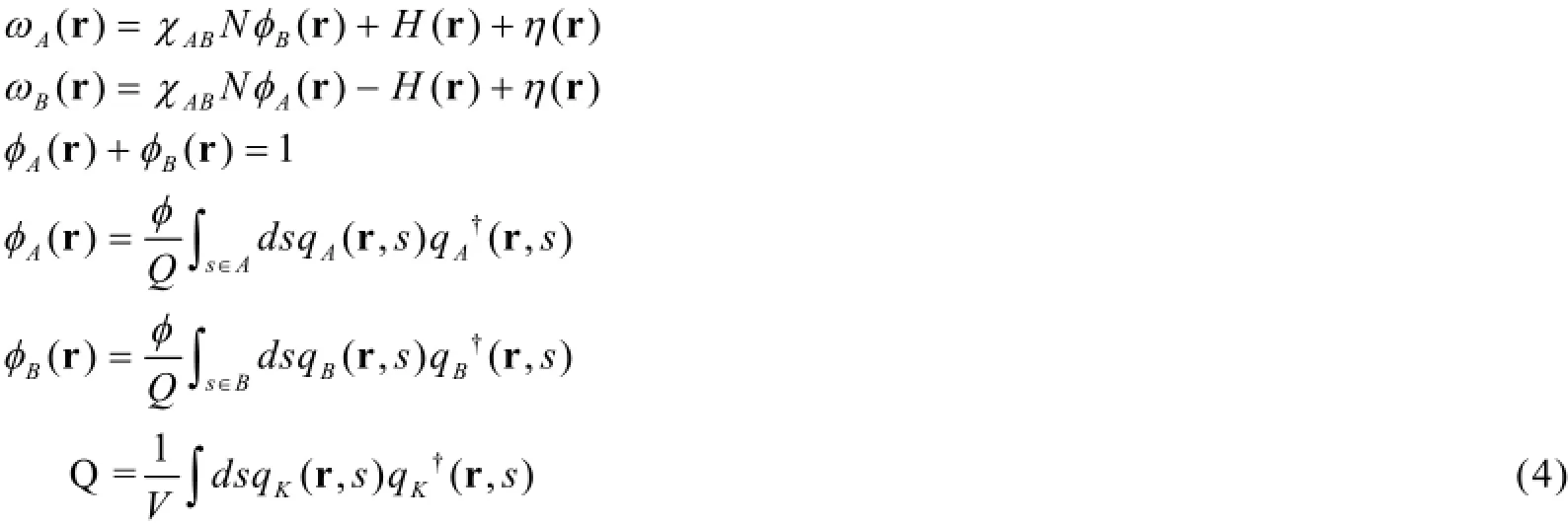
qK（r，s）和q†K（r，s）（K = A，B）为分子链的末端分布函数，表示末端固定在位置r的分子链上扩散至s位置的几率，两个函数均符合扩散方程，通过分步傅里叶法求解。我们参考线形嵌段共聚物的受限自组装［7］设置周期性边界条件，经过计算验证，将受限柱放置在一个格点离散成Nx×Ny×Nz= 64×64×64的三维立方盒子内，把分子链离散为1000个单元链节。

2　结果与讨论

星形嵌段共聚物（AB）f最显著的结构特点在于每一条臂都是相同的两嵌段。其中A嵌段的自由端与星形的核心相连，位于整个星形结构的内部，其分子链的运动都受到较大的限制；相对而言，B嵌段位于星形结构外部，受到星形结构的限制较小。A、B嵌段位置的不同造成相图左右不对称，与简单两嵌段共聚物A-b-B［7］相比，体积分数φA=0.2与φA=0.8两种星形嵌段共聚物（AB）f在柱状受限下的自组装不再一致，而且这种差异随着臂数增多而逐渐变大［8］。

2.1φA=0.2的（AB）f在吸引B嵌段的孔道内自组装

在（AB）f本体自组装相图中［7，8］，φA=0.2，ΧN/f=20的星形嵌段共聚物最稳定结构为柱状相（C）结构。其中体积分数较小的A嵌段构成柱，为分散相；柱体周围是体积分数较大的B嵌段连续相。我们以层状相周期L0为单位计量柱状空间的直径D，计为D/L0。柱状受限的相图（图1）中，红色表示分散相A，蓝色表示连续相B。当直径大约为1倍L0时，嵌段共聚物最稳定的结构为单柱结构C1A（上标A表示柱体由A嵌段构成，下标表示柱体数量），与本体自组装的C相结构一致。随着孔道直径增大，嵌段共聚物由C1A演变出丰富的三维结构，包括碟状结构DkA、单螺旋柱结构H1A、双螺旋柱结构H2A以及环状球状交替的结构TSA，继续增大半径，螺旋柱内部出现其他结构，例如H1CA、H2CA、H3CA等，三种结构能量相近，我们用H3CA表示。

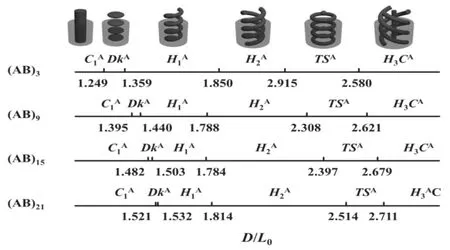
图1　φA= 0.2，ΧN/f =20的f臂星形嵌段共聚物在吸引B嵌段的孔道中受限自组装相图Fig.1 Phase diagramoff-arms star-like blockcopolymers atφA=0.2and ΧN/f =20 confinedin Bblock

星形嵌段共聚物（AB）f在吸引B嵌段的孔道中受限自组装与两嵌段共聚物A-b-B非常相似［7］，但是随着臂数增多，相区大小和相变位置发生了变动。C1A→DkA的相变位置逐渐右移，说明复杂三维结构需要更大柱状空间来满足分子链的拉伸需求。然而臂数增多使得每条臂之间的体积排除作用增大，高分子链构象熵减小，为了维持DkA结构的稳定性，需要相应的增大受限空间，这种趋势如图2所示。DkA和TSA可以看做螺旋角为0的特殊螺旋柱结构，H1A→H2A→H3CA的螺旋角依次增加［9］。随着臂数增多，我们发现螺旋角大的结构其相区有增大的趋势，螺旋柱的形成与高分子链的变形有关［9］，显然臂数增大不利于螺旋角度小的结构形成。

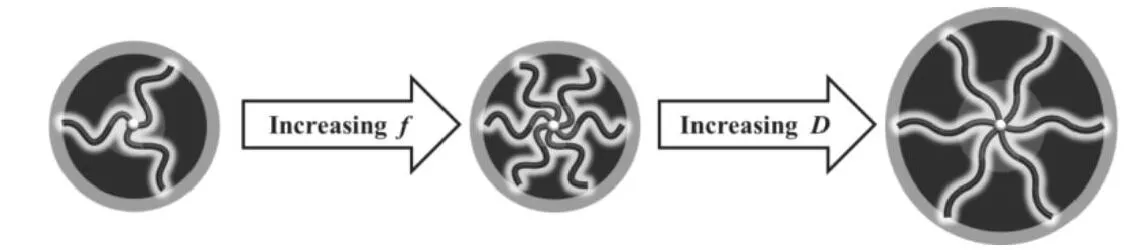
图2　结构稳定的维护进程Fig.2 The stages to keep the structural stability

图3　φA=0.8，ΧN/f= 20的f臂星形嵌段共聚物吸引A嵌段的孔道中受限自组装相图Fig.3 Phasediagramoff-arms star-like blockcopolymers atφA=0.8and ΧN/f =20 confinedin Ablock

2.2φA=0.8的（AB）f在吸引A嵌段的孔道内自组装

虽然φA= 0.8的星形嵌段共聚物本体自组装的稳态结构也是六方柱状相（C），但其柱状受限自组装复杂很多。图3中（AB）3的相图与图1较为一致。臂数少时星形结构的不对称性表现不明显，不论在其本体中［8］还是柱状受限下，相图都具相当高的左右对称性。当臂数增多至9臂时，出现了得到一种新的穿孔层（P2B）结构。臂数进一步增多至15臂、21臂时，螺旋柱结构的相区完全消失，出现新的相变序列C1B→P2B→P3B。穿孔层结构是一类变形的圆筒层（L1）结构［6］，我们以每一层平行存在的穿孔数量区别这些结构，用下标表示。

柱状相（C）为嵌段比例不对称结构，层状相（L）为嵌段比例对称结构，两者最重要的区别在于相界面曲率不同。构象熵作用下，体积分数较大的一相总有向体积分数较小的一相弯曲的趋势，当嵌段比例非常不对称时，层结构弯曲为柱结构。φA=0.8时（AB）9、（AB）15以及（AB）21在其本体相图中都位于柱状相区，却在柱状受限下自组装出变形的层状结构P2B、P3B，是孔道对A嵌段的吸引以及星形结构对A嵌段的限制共同作用的结果，两种作用极大降低了A嵌段的构象熵，减小了A嵌段与B嵌段之间构象熵的差别。随着臂数增多，这种共同作用逐渐增强，P2B、P3B等层结构逐渐代替了螺旋柱结构

当然，孔道对A嵌段的吸引仅作用在孔道截面的维度上，而在孔道的方向上，φA= 0.8的不对称比例仍然起到主导作用，造成的结果是层结构上出现穿孔。随着柱状空间直径增加，层上穿孔的孔洞相应变大，使得孔洞内A嵌段拉伸越来越严重，最终引起相变P2B→P3B。穿孔数量由每层2个增加至每层3个，每一个孔洞的尺寸相应减小，有效降低了A嵌段的熵自由能，这与螺旋柱数量的增大有相似之处。

继续增加柱状受限空间的尺寸，能够得到更为复杂的P3CB等结构；另外一方面，孔道内壁对嵌段的选择性、作用强度等因素在实际情况中远没有V0=±0.2这么简单。对于星形嵌段共聚物在柱状受限下的自组装，除了相图之外，仍然需要进一步的理论以及实验研究。

3　结论

本文应用自洽平均场理论研究了多臂星形嵌段共聚物（AB）f在柱状空间受限下的自组装。对于（AB）f来说，体积分数φA= 0.2与φA= 0.8两种嵌段共聚物并不对称。在吸引B嵌段的孔道中，φA=0.2的多臂星形嵌段共聚物自组装相图与简单两嵌段共聚物相似，但是随着臂数增多，相区大小以及相变位置都发生了变化。而在吸引A嵌段的孔道中，φA=0.8星形嵌段共聚物能够自组装出一系列新的结构C1B→P2B→P2B，随着臂数增多，穿孔层结构逐渐代替螺旋柱成为稳态结构。我们希望本研究能够为嵌段共聚物自组装的调控提供一些参考价值。

参考文献

［1］Matsen MW，Schick M. Stable and Unstable Phases of a Diblock Copolymer Melt［J］. Phys Rev Lett，1994，72（16）：2660

［2］Kim JK，Yang SY，Lee Y，et al. Functional Nanomaterials Based on Block Copolymer Self-assembly［J］. Prog Polym Sci，2010，35（11）：1325-1349

［3］Yu L，Chang GT，Zhang H，et al. Injectable Block CopolymerHydrogels For Sustained Release of a PEGylated Drug［J］. Int J Pharm，2008，348（1）：95-106

［4］Pang X，Zhao L，Feng C，et al. Novel Amphiphilic Multiarm，Starlike Coil-Rod Diblock Copolymers via a Combination of Click Chemistry with Living Polymerization［J］. Macromolecules，2011，44（18）：7176-7183

［5］Li W，Wickham RA，Garbary RA. Phase Diagram for a Diblock Copolymer Melt under Cylindrical Confinement［J］. Macromolecules，2006，39（2）：806-811

［6］Xu Y，Li W，Qiu F，et al. Self-assembly of 21-arm Star-like Diblock Copolymer in Bulk and Under Cylindrical Confinement［J］. Nanoscale，2014，6（12）：6844-6852

［7］Li W，Wickham RA. Self-assembled Morphologies of a Diblock Copolymer Melt Confined in a Cylindrical Nanopore［J］. Macromolecules，2006，39（24）：8492-8498

［8］Matsen MW. Effect of Architecture on the Phase Behavior of AB-type Block Copolymer Melts［J］. Macromolecules，2012，45（4）：2161-2165

［9］Li W，Qiu F，Shi AC. Emergence and Stability of Helical Superstructures in ABC Triblock Copolymers［J］. Macromolecules，2011，45（1）：503-509

Phase Diagram of Star-like Block Co-polymers Confined in a Cylindrical Self-assembly

WANG Chao，WANG Wen-jin，YE Shen-jie

School of Materials Science and Chemical Engineering/Ningbo University，Ningbo 315211，China

Abstract：The phase behavior of multi-arms star-like block copolymer confined in a cylindrical nanopore was investigated by using the self-consistent mean-field theory. We calculated the phase diagrams of cylinder-forming star-like copolymers with different number of arms f（f = 3，9，15，and 21）and two opposite volume fraction of A block（0.2 and 0.8 respectively）confined in a cylindrical nanopore. The phase diagram indicated that the influence of asymmetry on star-like copolymer and number of arms should not be ignored in this system. Surprisingly，a new perforated-lamellae-on-cylinder was observed in the stable phase array of φA= 0.8 with the A-preferential pore wall exhibiting different performance for the number of arms. The results in this work would be instructive in some extent for the regulation of block copolymers self-assembly.

Keywords：Star-like block copolymers；self-consistent field theory；self-assembly；phase diagram

中图法分类号：O631

文献标识码：A

文章编号：1000-2324（2016）03-0413-04

收稿日期：2016-03-04修回日期：2016-04-16

基金项目：浙江省新苗人才计划：多分散性对嵌段共聚物自组装在材料中应用的影响（2014R405090）

作者简介：王超（1990-），男，理学硕士，研究方向：计算机理论模拟，凝聚态物理. E-mail：wcboy77_2004@163.com